丰盈思考过程，形成策略意识

苏蓉蓉

[摘 要]当学生面临各种数学问题时，是否具有策略意识直接关系到问题能否顺利解决。以 “解决问题的策略——假设”教学为例，给出了在数学教学中培养学生假设策略意识的基本过程，即以问题为载体，为感悟假设埋下伏笔;经历问题解决过程，感悟假设策略的特点;呈现多样问题情境，丰富假设策略的经验;注重反思比较，实现假设策略的内化。

[关键词]思考;策略;意识;假设

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）32-0063-02

当学生面临各种数学问题时，是否具有策略意识，是否具备丰富的策略储备，是否能够适时做出正确的策略选择，直接关系到问题能否顺利解决。在小学阶段常用的解决问题的策略有画图、列表、找规律、假设等。从策略教学的目标来看，教师的教学不能局限于让学生获得正确的结果，更为重要的是要让学生在解决问题的过程中获得策略体验，形成一定的策略意识。下面笔者以 “解决问题的策略——假设”教学为例，论述在数学教学中培养学生策略意识的基本过程，期望能够起到抛砖引玉之效。

一、以问题为载体，为感悟假设埋下伏笔

古希腊哲学家亚里士多德认为：“思维从问题、惊讶开始。”问题是培养学生创新思维的引子，是调动学生创新思维的催化剂。在策略教学中，教师要以适切的问题为载体，使学生产生运用策略解决问题的内在需求，从而引发学生积极思考，为本节课的数学探究奠定基调。具体而言，问题的呈现要注意两点：一要注意从学生的生活实际出发。儿童的年龄特点和心理特征决定了他们学习行为的前提是“有趣的我才喜欢学”。小学数学新课标指出“让学生在生动具体的情境中学习数学”“让学生在现实情境中体验和理解数学”，这就告诉我们在创设问题情境时，要密切联系学生生活实际，顺应小学生以形象思维为主的思维特点，从而激发学生强烈的探究欲望，使“问题”真正起到引领学生思考的作用。二要注意问题设计要体现出假设策略的本质。教师在创设问题时要紧密结合教学内容，凸显假设策略教学的特点，使学生通过解决问题感受策略特点，形成策略意识。

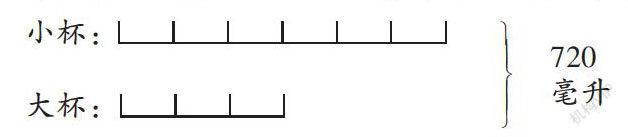
师（出示例1）：小明把720毫升果汁倒入6个小杯和1个大杯，正好都倒满。小杯的容量是大杯的1/3。小杯和大杯的容量各是多少毫升？

师：从题目中，你可以知道哪些数量关系呢？

生1：6个小杯的容量和1个大杯的容量共720毫升。

生2：  3个小杯的容量等于1个大杯的容量。

师：我们可以采用哪些办法解决这个问题呢？

生3：我可以列方程试试。

生4：我可以采取画图的办法。

……

结合学生的实际生活，创设生动情境，能有效激发学生的思考兴趣。教学中，教师呈现了一个“含有两种未知量，且这两种未知量存在倍比关系，求这两种未知量”的实际问题，这与学生以前遇到的数学问题既有相同点也有不同点，是对学生已有认知水平的拓展和延伸，具有一定的挑战性，为学生探究解决问题的策略做好了孕伏。

二、经历问题解决过程，感悟假设策略的特点

苏霍姆林斯基说：“在人的内心深处，都有一种根深蒂固的需要，这就是希望自己是一个发现者、研究者和探索者，而在儿童的内心世界中这种需要尤为强烈。”从学生的角度而言，掌握解决问题的策略与学习游泳颇有相似之处，只有经过反反复复的实践和磨炼，才能够享受到在水中的自由自在。因此，要让学生真正感悟策略本质，形成策略意识，需要讓学生经历解决问题的完整过程，并让学生在自主探索与合作交流中积累活动经验，感悟策略特点。

师：请同学们以自己的方式尝试解决例1中的问题。

生1：根据题意，小杯的容量是大杯的1/3，也就是大杯容量是小杯的3倍。因此我把1个小杯的容量设为x毫升，这样1个大杯的容量就是3x毫升。根据6个小杯的容量和1个大杯的容量等于720毫升，列出方程6x+3x=720，由此求得1个小杯的容量是80毫升，1个大杯的容量是80×3=240（毫升）。

师：这是运用了我们以前学过的方程思想。同学们还有其他解决途径吗？

生2：我是通过画线段图的方式来解决的。用一段线段表示1个小杯的容量，由于大杯容量是小杯的3倍，那么3段线段就表示1个大杯的容量（如下图）。

生2：从图中可以看出，720毫升果汁一共倒满了9个小杯，这样每个小杯的容量就是720÷9=80（毫升），进而求得1个大杯的容量是80×3=240（毫升）。

师：这是运用了画图的策略。有没有更简便的表达方式呢？

生3：假设把720毫升果汁都倒入小杯，把1个大杯换成3个小杯，这样正好倒满9个小杯，小杯的容量是720÷9=80（毫升），大杯的容量是80×3=240（毫升）。

生4：我和生3的思路差不多。假设把720毫升果汁都倒入大杯，把6个小杯换成2个大杯，这样正好倒满3个大杯，计算结果和生3一样。

师：生3和生4运用了假设策略。假设策略有什么特点？

生5：假设策略是把两个未知量（大杯容量和小杯容量）转化成一个未知量。

生6：假设策略使得数量关系变得更加简单了。

学生对于某个问题已经具备了固有的思考路径或解决模式后，就很难再把精力聚焦于其他解题策略，而只是热衷于按照自己的思路解答问题。然而，本节课的教学重点并非解决具体问题，而是引导学生感悟假设策略。当学生运用方程思想、画线段图的策略顺利解决问题后，教师通过不断追问“有没有更简便的表达方式？”，引导学生思考假设策略，凸显了假设策略的独特优势。

三、呈现多样问题情境，丰富假设策略的经验

学生在运用假设策略解决了“倒果汁”的问题之后，往往会误认为假设策略只是解决某个问题的方法。为了让学生拥有更大的探索空间，对假设策略形成更深刻、更全面的认识，在学生运用假设策略解决了倍数关系的问题之后，教师指导学生思考用假设策略解决相差关系的问题，从而丰富学生的学习体验，使学生感受到假设策略应用的广泛性。

师（出示例2）：在1个大盒和5个同样的小盒里面装满球，正好是80个。每个大盒比小盒多装8个，每个大盒和小盒各装多少个？

生1：我们可以尝试用假设策略解决问题。

生2：不行，刚才大杯容量和小杯容量之间是倍数关系，现在大盒容量和小盒容量之间没有明确的倍数关系。

生3：尽管二者之间没有倍数关系，但是“每个大盒比小盒多装8个”，明确了二者之间的数量关系。

生4：我是这样考虑的，1个大盒装球的个数加上5个小盒装球的个数等于80个，1个小盒装球的个数加上8等于1个大盒装球的个数。假设这6个盒子都是小盒，这样就会比1个大盒加上5个小盒的容量少8个，也就是装80-8=72（个），所以每个小盒装球的个数是72÷6=12（个），进而求得大盒装球的个数是12+8=20（个）。

师：如果假设6个盒子全部是大盒，可以吗？

生5：可以。如果假设6个盒子都是大盒，这样就能够多装8×5=40（个），所以6个大盒实际上装球的个数是80+40=120（个），每个大盒装球120÷6=20（个），每个小盒装球20-8=12（个）。

师：无论假设6个盒子都是小盒还是大盒，得到的结果都是一样的。请同学们比较这两种假设方法，说一说你更喜欢哪一种？

生6：全部假设成小盒，球的总数变少了;全部假设成大盒，球的总数变多了。

生7：我更喜欢全部假设成小盒，这样计算起来更加简便。

在策略教学中，解决问题并非最终目的，使学生体验策略的价值才是教学的关键。教师引导学生运用假设策略解决问题，并在异中求同，在同中辨异，从而启发学生依据题目特点选择简便的假设策略，不但概括提炼了假设策略的本质，还实现了策略的优化。

四、注重反思比较，实现假设策略的内化

荷兰数学教育家弗莱登塔尔教授指出 ：“ 反思是数学思维活动的核心和动力。”反思是学生不断感悟知识本质的必由之路。在学生充分体验解决问题的过程的基础上，教师要注重引导学生从多个角度对问题的解決过程和策略进行回顾和反思，这样才能帮助学生丰富对策略的感知，从而实现策略的内化。

师：我们在解决例1和例2的过程中都运用了假设策略，二者之间有什么不同点呢？

生1：例1的两个未知量是倍比关系，例2的两个未知量是相差关系。

生2：例1在假设后果汁的总量没有变化，例2在假设后装球的总量变化了。

生3：同一道题可以有两种不同的假设方法。

生4：在不同的假设方法中，要注意选择相对简单的。

……

在学生运用假设策略解决了不同数量关系的问题之后，教师及时引导学生进行反思、总结，从中提取不同问题中的相同策略——假设策略，从而使学生对假设策略的认知进一步清晰化，最终引导学生把假设策略建构在已有认知体系之中。

在学生的知识经验中本来就有运用假设的办法解决问题的经验，然而，这种经验是一种潜在的，也是无序的。本节课唤醒了学生已有的认知经验，使隐藏在学生潜意识中的假设策略变得清晰、深刻起来。学生经历了画图、交流、比较、归纳、反思等数学活动，感悟到用假设策略解决数学问题的独特优势，从而逐渐形成策略意识。

（责编 罗 艳）