离散数学课程思政案例设计与探索
2021-11-28段冉冉
段冉冉

摘要:根据教育部对高等学校课程思政建设的指导意见,为落实立德树人根本任务,以开放教育开设的离散数学课程中的“二元关系的矩阵和图”这一教学节段为例,开展了课程思政教学设计与探索。教学设计中,主要是思政元素与教学内容相结合,通过多个教学环节,对学生进行知识传授、能力培养和价值塑造。让学生理解有关概念的同时,培养了学生的逻辑思维能力、理论联系实际的科学态度和团结互助的团队精神。
关键词:离散数学;课程思政;教学设计
中图分类号:G642 文献标识码:A
文章编号:1009-3044(2021)28-0201-02
开放科学(资源服务)标识码(OSID):
2020年6月,教育部印发的《高等学校课程思政建设指导纲要》指出:“专业课程是课程思政建设的基本载体。要深入梳理专业课教学内容,结合不同课程特点、思维方法和价值理念,深入挖掘课程思政元素,有机融入课程教学,达到润物无声的育人效果。”[1]开放教育中,离散数学是面向国家开放大学的本科学生,对计算机科学与技术等专业开设的专业基础课程,教学内容有集合论、图论、数理逻辑等。该课程的概念多,内容抽象,逻辑性强,其教学目标是使学生具有现代的数学观点和方法,初步掌握描述工具和方法,培养学生具有抽象思维和缜密概括的能力,能够用所学知识分析和解决实际问题。如何将思想政治教育融入离散数学教学中,张学锋提出了九法,其中,思政元素与教学内容相融合的途径主要有七法[2]。徐公路提出了四种实施离散数学课程思政的具体方案[3]。王美艳、陈琳、张丽影等人分别就其专业课程中的某个知识点或教学节段进行了课程思政案例研究[4-6]。
二元关系的矩阵和图是《离散数学》第二章关系与函数中的一个教学节段。二元关系是满足一定条件的集合,函数是一种特殊的二元关系,二元关系的关系图都是图论中的图。可见,二元关系与集合、函数、图论关系密切。学生掌握二元关系的相关内容,不仅可以加深学生对集合和函数的理解,而且可以引导学生对后续的图论学习产生浓厚兴趣。如何挖掘该节段内容的思政元素,通过何种途径融入教学过程,笔者进行了课程思政教学设计与探索。
1思政教学目标
1.1知识素养
(1)理解二元关系的矩阵的概念;(2)理解二元关系的图的概念。
1.2能力素养
(1)在理解概念的基础上能够分析解决实际问题;(2)掌握描述问题的数学思维和方法。
1.3人文与科学素养
(1)能从中国女排比赛的激烈角逐中,对拼搏奋斗精神建立认同;
(2)能在小组讨论的学习过程中体会积极参与、不惧困难、团结互助的重要性;
(3)能从实际问题的解决中激发学习兴趣,明白数学观点和方法背后的现实意义,加深对知识内容的理解,具有开拓专业理论学习的素质。
2思政融入点
2.1将现实生活中的实际问题抽象成二元关系的问题——理论联系实际
离散数学的研究对象是离散的点,离散的点之间可以建立联系,因此可以利用实例来帮助理解抽象的理论。二元关系的矩阵和图是二元关系的两种表示方法,是学生要学习的新内容,而二元关系的集合表示方法是学生刚刚已经学习过的内容,学生比较熟悉。通过一个教学情境,将现实生活中的实际问题抽象成二元关系的问题,提出三个问题,引导学生明白二元关系的三种表示方法虽然不同,但描述的都是同一个对象,不同表示方法之间可以建立联系。
2.2以中国女排为榜样激发学生的拼搏奋斗精神
利用多媒体展示中国女排在2019年第十三届世界杯女子排球赛的比赛现场的图片和播放该比赛中某个激动人心时刻的小视频。让学生感受比赛现场激烈角逐的气氛,同时体会在比赛中,中国女排体现的不屈不挠、顽强拼搏、团结协作、永不放弃的精神。
2.3合作式学习培养学生团队精神
在学生已预习新知的基础上,通过小组合作讨论、教师观察指导,让学生主动建构新知。小组合作的学习方式,有利于调动学生主动参与课堂的积极性,有利于培养学生的竞争意识和团队合作精神,学生主动分析和解答的过程有利于培养学生的思维和语言能力。
3 教学过程与实施
3.1 课前
让学生预习教材中该节段的内容,并登陆国家开放大学学习网观看离散数学的课程导学中的“关系概念与表示”“二元关系的表示方法”等微视频。
3.2 课堂
1) 课堂导入:向学生展示中国女排在2019年第十三届世界杯女子排球赛的比赛现场的图片和小视频,让学生发表观看后的想法,并对学生进行关于拼搏奋斗的思想政治教育:没有随随便便的成功,“不经一番寒彻骨,怎得梅花扑鼻香”?比赛如此,学习也是如此。“困难如弹簧,你强它就弱,你弱它就强”,离散数学课程内容虽然比较抽象,但要不惧困难,在平时就稳扎稳打,坚定自己能够熟练掌握所学内容的信念。学习要讲究方式方法,要有竞争意识,同时也要互帮互助,在理论学习的同时,也要多关注现实生活,学会用所学知识解决现实问题。
紧接着设置一个和比赛有关的教学情境:有甲乙丙丁四支球队进行单循环比赛,每两支球队比赛,只记胜负,没有平局。比赛结果如下:甲队战胜乙队和丙队各一次,乙队战胜丙队和丁队各一次,丙队战胜丁队一次,丁队战胜甲队一次。并向学生抛出三个问题,问题1:你能用集合表示上述比赛结果吗?问题2:你能用矩阵表示上述比赛结果吗?问题3:你能用图表示上述比赛结果吗?
2) 讲授新课:对于第1个问题,因为集合的概念比较大,可以启发学生用刚学过的知识解决问题:在中学阶段,同学们已经知道,集合的表示方法有列举法、描述法和圖像法,在前面的课程学习中,同学们已熟练掌握了用列举法和描述法分别表示任意集合A上的关系R。并通过举例:设[A=1,2,3],R是A上的关系,如果用描述法表示,有 [R=
其中,[R1=<1,2>,<1,3>],[R2=<2,3>,<2,4>],[R3=<3,4>],[R4=<4,1>],分别表示甲队、乙队、丙队和丁队的比赛结果。
对于第2个和第3个问题,可以把关系矩阵和关系图的定义告诉学生,然后让学生分组讨论,并指定小组代表回答。对于定义的理解,学生可以借助学习平台上课程导学中的“关系概念与表示”“二元关系的表示方法”等微视频获得帮助,尤其是“二元关系的表示方法”,该视频以动画的形式把关系矩阵和关系图中的元素特征进行了动态描述,更有利于学生理解和掌握。
对于第2个问题,小组学生代表的回答如下:由第一个问题的结果可知
[A=1,2,3,4],
[R=<1,2>,<1,3>,<2,3>,<2,4>,<3,4>,<4,1>],[rij]是矩阵[MR]中的元素,当[i=1,j=1]時,[xi=1,xj=1],[∵<1,1>?R],[∴r11=0]。当[i=1,j=2]时,[xi=1,xj=2],[∵<1,2>∈R],[∴r12=1]。同理,[r23=1],[r24=1],[r34=1],[r41=1],其余元素[rij=0]。则R的关系矩阵是
[MR=0110001100011000]
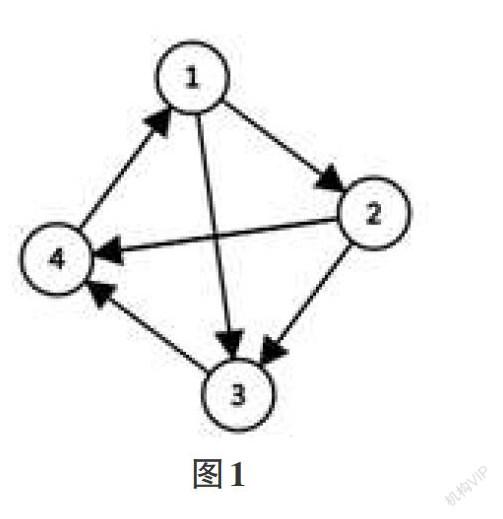
对于第3个问题,小组学生代表的回答如下:上面的例子中,由 [<1,2>∈R],[<1,3>∈R]可知,由1到2,1到3分别有一条有向边。同理,由2到3,2到4分别有一条有向边,由3到4有一条有向边,由4到1有一条有向边。因此R的关系图[GR]可以用图1来表示。
3.3课后
小结和练习巩固:经过上面的学习和讨论,学生已经比较好地掌握了二元关系的矩阵和图的相关内容,趁热打铁,教师给学生布置小练习进行及时巩固。
知识拓展:为进一步激发学生的学习动机,结合学生所学的计算机科学与技术的专业优势,针对如何在计算机上画关系图,向学生布置兴趣作业,给学生推荐画关系图的网站:https://csacademy.com/app/graph_editor/,和画关系图的软件:Gephi。鼓励学生充分利用网络资源,在网上搜索更多方便好用的方法进行学习。
4 课程思政教学效果评价
(1)知识层面
理解二元关系的矩阵和图的概念,并能够用数学语言表达。
评价方式:课堂小组讨论过程中,学生的表现和解答情况,及学生课后作业的完成情况。
(2) 能力层面
在理解概念的基础上,能够用矩阵和图表示现实中的二元关系,能够团结协作克服困难。
评价方式:课堂小组讨论过程中,学生的表现和解答情况,及小组代表的解答情况。
(3)素质层面
理解和体会数学知识背后的现实意义,学会理论联系实际。
评价方式:增设兴趣作业,让学生自己提出能够体现二元关系的实际问题并能用二元关系的矩阵和图表示。
5结语
如何在离散数学中进行课程思政教学,本文以二元关系的矩阵和图这一教学节段为案例,主要通过结合生活实际的例子、利用多媒体展示思政元素(图片、视频)并适当解说与引导、合作式学习讨论,开展了思政元素与学科知识相融合的教学设计与探索。通过课前预习、课堂导入、讲授新课、小结和练习巩固、知识拓展等教学环节,对学生进行知识传授、能力培养和价值塑造,过程科学合理。课程思政教学让学生在理解有关概念的同时,培养了学生的逻辑思维能力、理论联系实际的科学态度和团结互助的团队精神。离散数学课程思政的教育教学,仅凭教学设计的研究是不够的,还需要在教师的育人能力与素质、教学大纲的制定、教材的编写和选用、课堂的组织形式与教学模式、教师和学生的评价机制等方面不断地进行探索、实践、改革和创新。
参考文献:
[1] 教育部关于印发《高等学校课程思政建设指导纲要》的通知[EB/OL].http://www.moe.gov.cn/srcsite/A08/s7056/202006/t20200603_462437.html,2020-06-01.
[2] 张学锋.离散数学课程思政教育初探[J].教育现代化,2019,6(98):284-285,293.
[3] 公徐路.课程思政下离散数学课堂教学中的改革与实践[J].大学数学,2020,36(4):25-30.
[4] 王美艳,黄超,张长平,等.《大气污染控制工程》课程思政教学设计的探索与实践[J].决策探索(下),2021(1):77-78.
[5] 陈琳,朱晔.课程思政在《离散数学》中的应用——以“赋权树”为例[J].电脑知识与技术,2020,16(23):125-126.
[6] 张丽影,那立艳,王茹,等.无机与分析化学实验课程思政案例设计与探讨[J].广州化工,2021,49(5):181-183.
【通联编辑:王力】
