基于时变C-Vine-Copula 的风险价值度量

2021-11-28虞情李晋枝中央民族大学

品牌研究 2021年9期

文/虞情李晋枝（中央民族大学）

一、引言

金融风险的本质是损失的不确定性，现代金融管理中这种不确定性并不是孤立的，需要考虑多变量之间的关系，多变量之间可能会因此存在着传染效应。经济资本的测算依据和核心技术在于风险计量，从数据过滤到金融建模再到数据仿真，以及风险测算和回溯检验，概括了经济资本风险计量的整个过程。

VaR 是现代金融风险计量常用的指标，本文以VaR 开展风险研究。为了度量多元变量之间的非线性相关关系，本文借助时变C 藤Copula的方法。Copula 函数经历了从二元到多元，静态到动态，传统多元到藤结构的研究阶段，现在已经比较成熟，也有许多经典的文献可以查阅借鉴。Copula 由Sklar（1959）引入并提出了Sklar 定理；Embrechts et al.(2003)用Copula 函数计算资产组合的VaR 值；Patton(2001)首先研究时变Copula 函数，令时变参数服从类似于ARMA 过程；Creal（2008）凭借GAS 模型将动态Copula 函数的建模应用在函数种类上拓展到了阿基米德函数的动态模型；Bedford and Cooke（2001，2002）对二维情形开展研究，分别设定Pair-Copula，从而简化了估计方法。近年来，全球经济的不确定性以及股票和债券市场的高度波动，刺激了投资者将黄金和其他贵金属纳入投资组合的兴趣。贵金属是一种有用的对冲工具，因为它们对其他金融资产的依赖性较低，当金融市场出现极端的市场波动时，贵金属可能会表现出避险资产的特征。因此，本文以金、银等六种贵金属为研究对象，以基于GAS（1,1）理论的C-Vine-Copula 为研究方法，用蒙特卡洛模拟法计算这六种贵金属资产组合的VaR。

二、研究方法

（一）C-Vine-Copula 模型

考虑一个n维随机向量带有联合密度函数和分布函数F(x1,x2,…,xn)，根据Sklar（1959）定理，该随机向量的联合分布函数可以用Copula 函数表示为：

其中C(•)是Copula 函数，Fi(xi),i=1,…,n是随机变量Xi的边缘分布函数。当Fi(xi)都连续时，C(•)唯一确定。对于随机向量X的联合密度函数可以分解为条件函数形式：

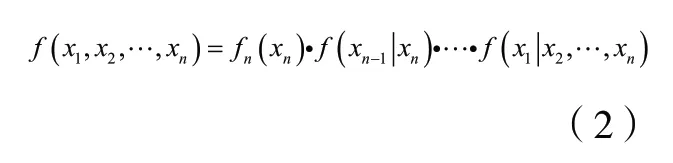
在多元相关性中获得更大建模灵活性的一种方法是进行Pair-Copula 分解，即将n元联合密度函数分解为个二元Pair-Copula 密度函数与其边缘密度的乘积，这种分解被称为Vine Copula。因为Pair-Copula 的分解不唯一，为了使分解更加规范，Bedford &Cooke（2001,2002）引入了正则藤结构，即R-Vine。该结构包含节点以及连接节点的边和树结构，每条边就代表一个二元Pair-Copula 函数。常用的正则藤包括C 藤（C-Vine）和D 藤（D-Vine），本文基于C 藤进行研究。

定义1（C 藤）：当满足以下条件时，则称V为建立在n维变量的C藤结构：

（1）V=(T1,… ,Tn−1)，Ti是构成C 藤结构的树；

（2）第i棵树的边是第i+1棵树的节点，且第i棵树上拥有共同节点的两条边在第i+1棵树上是相连的；

（3）第i（i=1,2,…,n−1）棵树Ti有唯一的节点与n−i条边相连，该节点称为这棵树的主节点，除主节点之外的其他节点仅连接一条边。

C-Vine 结构的n维联合密度函数由下式给出：

其中j代表第j棵树，k代表第j棵树中n−j条边的遍历。

（二）基于GAS 的二元时变Gaussian Copula

基于GAS 理论的Copula 时变参数的演化模式如下：

其中，ρt为Copula函数在t时刻的参数向量，Λ (•)为修正的logistic 转换函数对参数ft进行变换，ω、Ai(i=1,...,p)、Bj(j=1,...,q)为演化方程系数，令c(•)是Copula函数的密度函数，则为得分向量，是比例矩阵。令基于GAS(p,q)理论的时变二元正态Copula 函数的密度函数为：

（三）VaR 的计算

VaR 即风险价值模型，对于一个投资组合的VaR，其定义为：

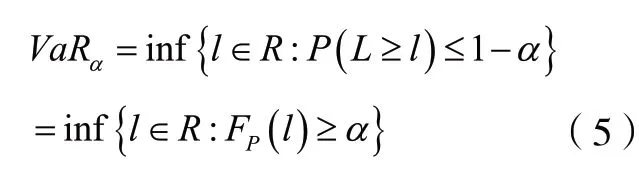
其中显著性水平α∈(0,1)，投资组合的损失为L，即VaR 是使该投资组合的损失L超过l的概率不超过（1−α）的最小的l。若有n个投资对象，第i个投资对象在整个资产组合中所占的份额为iδ，那么整个投资的资产组合收益率为：

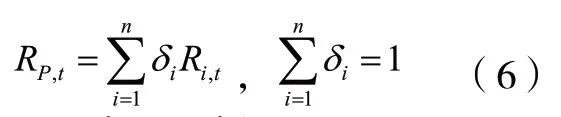
三、实证分析

本文选取六个比较具有代表性的贵金属每日收盘价为研究对象，包括金、银、铅、钯、铜、镍，时间从2014 年6 月到2021 年3 月。计算其对数收益率序列：

（一）描述性分析

计算对数收益率序列的主要统计特征，得到表1。

由表1 可知，对于偏度来说，金和铅呈右偏分布，其余四种贵金属呈左偏分布；对于峰度而言，金、银、钯的收益率序列峰度高于3，具有厚尾特征。J-B 正态性检验的结果在显著性水平0.05 下都拒绝服从正态分布的假设。接着对序列进行平稳性检验和ARCH 效益检验显示序列平稳且具有ARCH 效应，可以对边缘分布拟合ARMA-GARCH模型。

表1 对数收益率时间序列统计特征

（二）拟合边缘分布

根据AIC 准则，对ARMAGARCH 模型定阶，找到最优的ARMA-GARCH 模型如表2 所示。

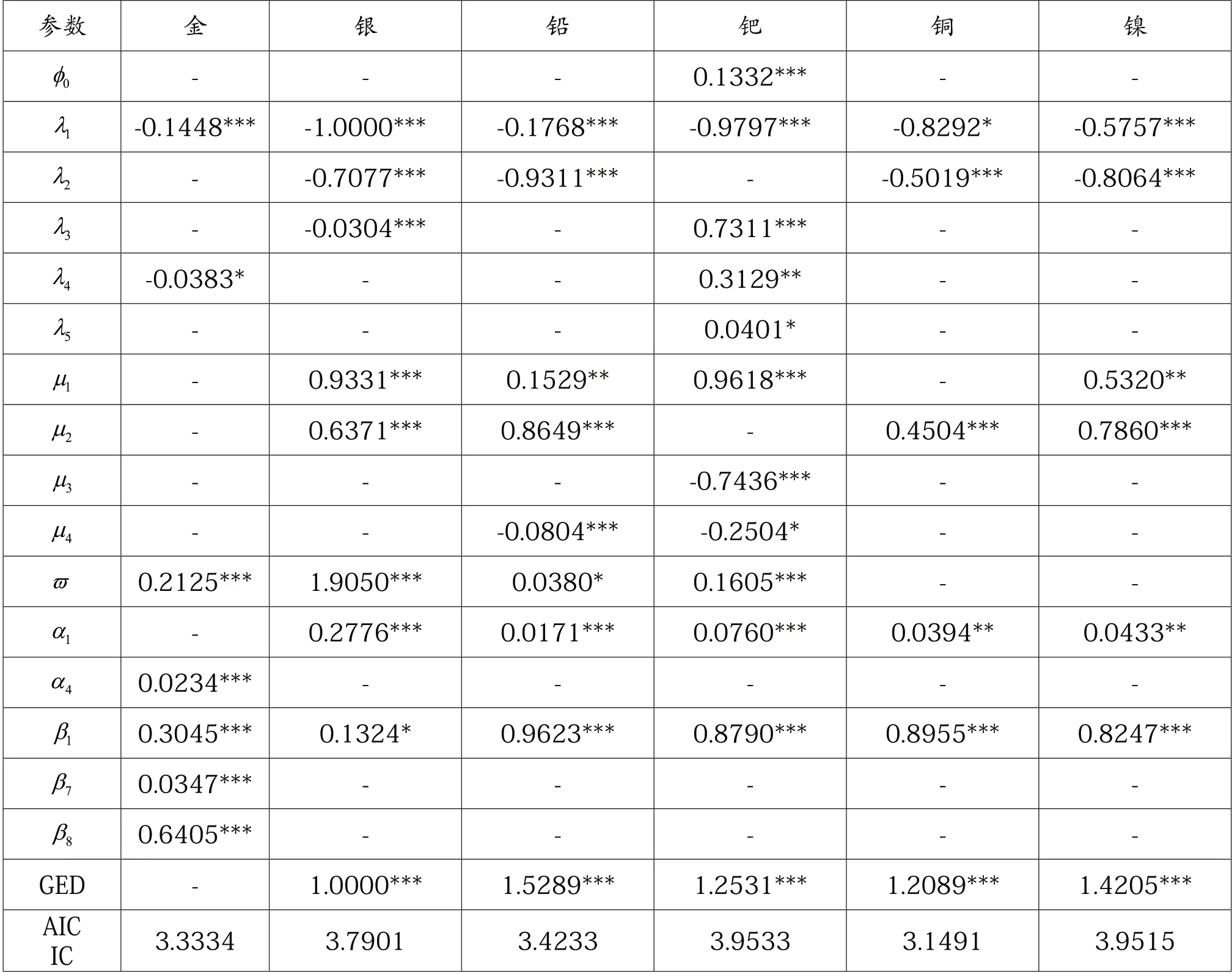
表2 ARMA-GARCH模型参数估计结果

对模型得到的标准残差序列进行ARCH 效应检验和白噪声检验，结果显示残差为白噪声序列且不具有ARCH 效应，可见拟合的模型可以较好地刻画各贵金属的对数收益率序列的边缘分布。

（三）拟合时变C-Vine Copula

1.概率积分变换

对拟合边缘分布得到的标准化残差序列进行概率积分变换，K-S检验p 值都大于0.05，变换后的序列服从（0,1）上的均匀分布，可以拟合Copula 模型

2.主节点的确定

要拟合C-Vine-Copula，就得确定每棵树的主节点，计算概率积分变换后序列间的相关系数，按相关系数从大到小排列，最大的即为主节点：从第二棵树开始，计算条件概率序列的Kendall 秩相关系数，依次确定每棵树的主节点，得到基于GAS（1,1）理论的C-Vine Gaussian Copula 的结构及模型参数估计如表3。

表3 基于GAS(1,1)的C-Vine-Copula 模型参数估计结果

4.VaR 的计算

下面通过蒙特卡洛模拟法计算六个贵金属组合的VaR，先根据前面建立的C-Vine-Copula 模型拟合6个独立同分布的序列，服从（0,1）均匀分布；再将这六个序列逆向推导出服从GAS（1,1）C-Vine Copula中Pair-Copula 分解的联合分布函数的仿真序列，并通过概率积分变换将其转换为模型的标准残差序列；最后根据拟合的边缘分布ARMAGARCH 模型将标准残差序列转化为收益率序列，并据此计算六个序列的组合收益率，重复计算1000 次，即可得到相应显著性水平下的VaR值（见表4）。