基于Shiny 与Leaflet 技术的中国邮递员问题网页设计与开发

亓玉潇，张 昆

（华东师范大学 地理科学学院，上海 200241）

0 引言

街道喷洒消毒液是新冠肺炎疫情期间的重要防疫措施。假设有若干条道路需要消毒，消毒车辆走怎样的路线既能够完成作业，又可使总路程最短，这便是一个路径优化问题。除此之外，警察巡逻、垃圾车收集垃圾、扫雪车清扫街道、街景图摄制等均涉及路径优化问题，可统称为中国邮递员问题（Chinese Postman Problem，CPP）［1］。CPP 最早由管梅谷［2］提出，即一个邮递员从邮局出发，经过需要投递信件的每条街道然后返回邮局，应该走怎样的路线以使总里程最短。CPP 是欧拉环游的扩展，欧拉环游是寻找经过每条边一次，最后回到起点的路线；CPP 则是寻找经过每条边至少一次，最后回到起点，且总里程最短的路线。相比之下，CPP 具有更广的应用领域。

Shiny 是一个R 语言包，可以应用R 语言构建交互式Web 应用程序［3］。开发者无需了解开发网页的HTML、CSS或JavaScript 等传统技术，直接使用R 语言便可以完成服务器端和前端网页开发，应用程序可免费托管在Shinyapps.io云端并获得一个网址，用户访问该网址即可使用应用程序。Leaflet 是用于交互式地图开发的JavaScript 库，Leaflet R 包用R 语言封装了JavaScript 命令［4］。将CPP 应用于解决实际问题的软件和程序并不多见，若能以CPP 为基础借助以上开源软件开发一个供道路作业人员使用的应用程序，可为其工作开展提供便利。

1 相关研究

目前对于CPP 的研究主要集中在算法改进和模型扩展（如带风向的邮递员问题、乡村邮递员问题等）方面。CPP为非确定性多项式（Nondeterministic Polynomially，NP）类问题，关于求解算法，管梅谷［2］提出了奇偶点图上作业法，该方法适用于规模较小的CPP 问题；Edmonds 等［5］提出了更为有效的最优匹配算法；也有一些研究采用启发式算法求解该类问题［6-8］。

国内外均有借助Shiny 进行网页开发的案例。例如，李玲玉等［9］应用Shiny 技术开发了用于快递员配送路径规划的网页应用Delivery Helper；陆瑶等［10］以降水监测数据作为输入，借助Shiny 技术开发了山洪预警系统；白秀显［11］借助Shiny 技术实现了高校招生数据的挖掘与可视化；Zhou等［12］基于用户创造内容（User-Generated Contents，UGC）开发了旅行规划工具，在利用地理空间数据挖掘方法获取酒店信息、路线费用等内容后开发了网页界面，为用户提供景点酒店、旅游路线等综合建议。Shiny 技术与Leaflet 结合可以实现网页地图数据的可视化与交互性，例如Edward等［13］基于Shing 与Leaflet 技术开发了全球新冠疫情地图COVID-19 tracker，在一张世界地图上展示了每个国家的疫情分布情况，数据每日更新。本文基于Shiny 与Leaflet 技术，开发了一个求解CPP 类问题的网页应用程序Chinese Postman Problem Solver（CPP Solver，https：//qiyuxiao.shin⁃yapps.io/myapp1/），为道路作业人员规划最优路线。

2 CPP 建模与求解

含有欧拉环游的图称为欧拉图，一个连通图是欧拉图的充分必要条件是图中每个顶点的度数均为偶数。CPP 与欧拉图密切相关，如果CPP 对应的连通图是欧拉图，则可采用Fluery 算法找出欧拉环游（回路），该环游即为CPP 的最优解；如果CPP 对应的连通图不是欧拉图，则图中必定存在度数为奇数的顶点（奇点）。一个图中奇点的个数必定为偶数，因此可将奇点两两匹配，找出任意两个匹配奇点之间的最短路径，在该路径上添加重复边，将奇点的度数变为偶数，即可构造出欧拉图。CPP 的关键是找出重复边长度最短的奇点匹配方式。只有2 个奇点的连通图是最简单的情况，因为只有1 种匹配方式；若有4 个奇点，则有3 种两两匹配的方式；若有6 个奇点，第一个奇点便可与另外5 个奇点中的任意一个匹配，一旦匹配，便只能剩下4 个奇点进行匹配（3 种），因此共有5×3=15 种匹配方式。以此类推，n个奇点的匹配方式数为：

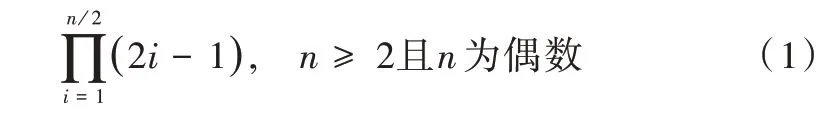
根据式（1），10 个奇点的匹配方式有945 种，20 个奇点则有654 729 075 种之多，显然不能采用枚举算法。计算机一般只能枚举十几个奇点，不能满足实际应用需求。本文采用整数规划模型找出最佳匹配方式，以图1 为例，假设有4 个奇点，所有可能的两两匹配构成了一个完全图，每条边上的数字代表权重，即两个奇点之间最短路径的长度，图1右侧则是对应的距离矩阵。

Fig.1 Complete graph and distance matrix of four singularities图1 四奇点完全图与距离矩阵

定义决策变量xij表示奇点i与j是否匹配，xij等于1 表示匹配，等于0 表示不匹配。ωij表示奇点i与j匹配的权重，即i、j之间最短路径的长度。对于每个奇点而言，其必须与另一个奇点匹配，且只能匹配一次。以奇点1 为例，约束条件为：

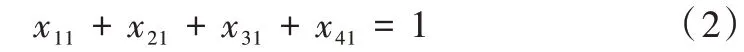
该约束对应距离矩阵的第一列。为避免自身匹配的情况，将距离矩阵的对角线元素设置为很大的值（9 999）。规定若xij等于1，则xji也等于1，因此得到以下整数规划模型：

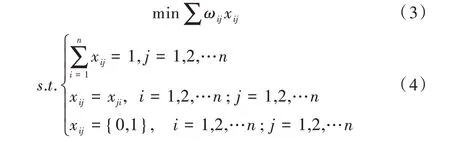
式（3）为目标函数；式（4）为约束条件，其中第一项对应距离矩阵的每一列。采用R 语言的Rglpk 包求解整数规划，求解100 个奇点的匹配用时不超过5s。图1 的最优匹配为奇点1 与3 匹配，奇点2 与4 匹配，即x13=x31=x24=x42=1，其他xij=0，目标函数的值为16，其值的一半（8）即为重复边的长度。

确定了奇点匹配的方式后，便可在CPP 对应的图上添加重复边，构造出欧拉图G，然后采用Fleury 算法求出欧拉回路。Fluery 算法的主要思想为从一个顶点出发，能不走桥就不走桥［14］，算法步骤为：

（1）任取一顶点v0，令W0=v0。

（2）设已经选定的迹Wi=v0e1v1e2…eivi，按以下原则从E（G）-｛e1，e2，…，ei｝中选取边ei+1：①ei+1与vi相关联；②除非没有别的边可供选择，否则ei+1不是G-｛e1，e2，…，ei｝的桥（割边）。

（3）重复步骤（2），直至E（G）-｛e1，e2，…，ei｝为空。

3 网页开发

Shiny 应用程序由用户界面对象（UI）和服务器函数（server）组成，UI 负责应用程序的布局，server 负责程序的功能实现并控制输出。采用grid layout 布局整个页面，以便控制模块列宽，使用到的主要控件包括：leafletOutput 用于显示地图；textOutput 控件用于输出文字；actionButton 创建按钮“Finish Clicking”“Clear”和“Generate Route”；selectIn⁃put 控件允许用户从列表中选择起点。Shiny 也提供了构建HTML 文档的简单函数，如hr（添加横线）、h3（添加标题）等。

Fig.2 User interface（Website：https：//qiyuxiao.shinyapps.io/myapp1/）图2 用户界面（网址：https：//qiyuxiao.shinyapps.io/myapp1/）

如图2 所示，程序的使用包括两个步骤：首先采用鼠标在地图上选择一个连通的道路网，这些连通的道路即为需要至少经过一次的服务边，点击按钮“Finish Clicking”后，程序会对选中道路的路口进行编号；然后选择一个路口作为起点，或用缺省的1 号作为起点，点击按钮“Generate Route”求解路线规划。

CPP 的解是一条经过服务边至少一次，且回到起点的最短路径。由于经常会有重复边（经过两次的道路），最佳路径的行走次序往往难以清晰表达。为了便于用户查看，本文提出邮递员路径分解算法，步骤为：

（1）设T=ø。

（2）欧拉回路记为C=｛v1，v2，…，vn｝，遍历C 中的顶点，记当前顶点为vi。

（3）T=T∪C，算法结束，T 中保存的即为分解后的路径。

该算法的思路为依次判断最终路径中是否有重复经过的路口，如果有，则将路径分解为两部分，一部分路径没有重叠部分，然后对另一部分的路径重复前面的判断。算法中对v2=v1的情况进行了判断，是考虑到了环路的情形。如图3 所示，加粗的路线是需要经过的服务边，起点为顶点3，最优路径的顶点序列为｛3，2，1，2，2，3｝。顶点序列对于用户而言是不直观的，而图形显示可能有二义性，例如从顶点3 走到顶点2 后，是经过环路回到顶点2，还是直接走到顶点1。采用分解算法对该条路径进行分解，得到4 段路径：｛3，2，1｝，｛1，2｝，｛2，2｝，｛2，3｝，在图形窗口中依次显示这4 段路径，既直观又不会造成误解，因为没有重叠部分。

Fig.3 Optimal path with loop图3 带环路的最优路径

道路网数据是解决CPP 必不可少的组成部分。本文道路网数据来自OpenStreetMap 官网（https：//www.openstreet⁃map.org），在地图中定位到研究区域后，点击页面上方的“导出”按钮，可将矢量数据导出为osm 文件。在QGIS 软件中对道路图层（map lines）进行必要的编辑，如将断开的道路合并、两条道路在交叉点打断等。采用R 语言的rgdal 包将处理好的道路网读取并加载到leaflet 中，具体技术框架如图4 所示。

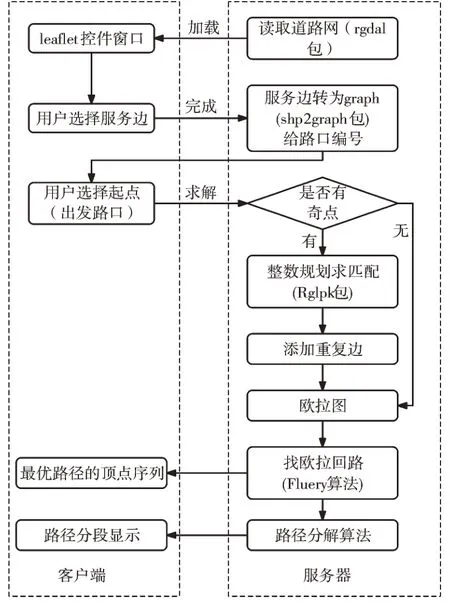
Fig.4 Technical framework图4 技术框架

4 案例分析

对图5 所示的目标道路案例进行路径规划，将3 号点设定为起始点，需要作业完成加粗路线部分，求解出一条最优路径。结果路径如图6 所示，总路径（route_undecom⁃posed）为3-1-2-1-4-7-4-5-8-5-11-6-10-9-10-13-10-12-15-12-16-11-14-11-6-1-3，分解后为route1：3-1-2；route2：2-1-4-7；route3：7-4-5-8；route4：8-5-11-6-10-9；route5：9-10-13；route6：13-10-12-15；route7：15-12-16-11-14；route8：14-11-6-1-3，总路线长度 为2 808m。由图5 可知，目标道路构成的原图中共有12 个奇点，经过模型匹配的结果为2 和3、4 和7、5 和8、9 和13、6 和14、12和15。原图中共有17 条边，添加边生成的欧拉图中有26条边，共重复了9 条边，分别为1 和2、1 和3、4 和7、5 和8、9和10、10 和13、6 和11、11 和14、12 和15 之间的边。原图有1 850m，重复边有958m。

Fig.5 Target roads图5 目标道路

Fig.6 Route planning results图6 路线规划结果

5 结语

CPP 是为数不多的由中国学者提出的路径优化问题。如果道路网中没有奇点，CPP 的求解就等同于寻找一个欧拉回路；如果存在奇点，则寻找奇点的最优匹配方式是解决CPP 的关键。本文建立了一个整数规划模型，可以快速求解上百个奇点的匹配。在此基础上，借助开源Web 工具Shiny 建立了一个求解CPP 的网页应用程序CPP Solver，为国内推广应用Shiny 进行网页开发提供了案例，其中还用到了leaflet 技术显示地图并加载道路图层。如果存在需重复经过的道路或路口，CPP Solver 能采用路径分解算法对最优路径进行分段，消除了路径导航可能产生的二义性，进一步优化了结果的可视化程度。然而，CPP Solver 也存在一些不足：①只能处理道路网连通的情况，即经典CPP，下一步可考虑对不连通情况下的乡村邮递员问题建模并进行网页开发；②研究区域的道路网是CPP Solver 的基础，而道路网的编辑与处理需要一定的GIS 专业知识和技术，当研究区域较大时，道路网编辑的工作量会大大增加，这在一定程度上制约了CPP Solver 的推广；③CPP Solver 没有考虑复杂的交通规则，例如单行道、车辆拐弯的限制等，以后可针对混合图中的CPP 建模求解。