融合聚类过采样算法的信贷不平衡数据分类

樊东醒，叶春明

（上海理工大学 管理学院，上海 200093）

0 引言

不平衡数据广泛存在于信用风险评估［1］、网络异常监测［2］、机械故障诊断［3］和新冠病毒疾病诊断领域［4］，在信用风险评估领域中，若将“坏客户”误判为“好客户”将会造成极大的损失风险。夏利宇等［5］认为，提升模型对不平衡数据的分类效果已成为信用评级领域的研究重点之一。

传统分类器对不平衡数据的分类通常倾向于多数类，如支持向量机（SVM）［6］、K 近邻算法（KNN）［7］和神经网络［8］等，针对这一问题目前主要有3 种解决方法：抽样法、代价敏感学习、集成学习分类［9］。代价敏感学习和集成学习方法作用于算法层面，抽样法作用于数据层面，通过插值和抽样等方式以重新达到类别平衡，通常可与集成学习模型相结合以提高分类效果。

抽样法包括过采样和欠采样两种，其中最经典的过采样方法是SMOTE 算法［10］，它通过合成少数类样本对抗不平衡，但存在泛化和高方差问题，并影响数据分布特征［11］。针对这一问题，Borderline-SMOTE［12］和ADASYN［13］根据少数类K 近邻中危险点数目调整采样策略。Douzas 等［14］提出K-meansSMOTE，其使用K-means 进行聚类分簇采样，并根据密度分配采样权重，该方法有效缓解了类间不平衡，但是由于K-means 聚类的局限性，存在孤立点敏感和边界样本损失问题；针对K-means 聚类，韩旭等［15］指出它会破坏掉两类数据之间的空间结构，从而造成边界样本损失。此外，当K-means 应用于不平衡数据时存在“均匀效应”，导致边界样本被划分到邻近大类中［16］。针对以上问题，本文提出了一种融合K 中心点聚类和边界阈值的过采样方法，通过确定边界阈值，选择适合聚类的区域范围，避免远离类边界样本的干扰，并通过改进K 中心点算法使聚类结果更加“紧凑化”。此外，本文提出了适用于不平衡数据的聚类K 值寻优方法，并通过实验验证了所提方法的有效性。

1 K 中心点算法改进

1.1 K 中心点算法

K 中心点算法是一种针对K-means 孤立点敏感问题提出的改进方法，具体步骤如下：①输入数据集和聚类个数K；②在样本中随机选择K 个点作为各簇的中心点；③计算其余点到K 个中心点的距离，根据每个点到K 个中心点的最短距离，划分到最近的簇；④在每个簇中按照顺序依次选取候选点，计算该点到当前簇中所有点的距离之和，将距离代价最小的点作为新的中心点；⑤重复②③④步骤，直到各簇的中心点不再改变；⑥输出K 个簇。

1.2 改进的K 中心点算法

在使用K-means 等算法划分类簇时，处于稀疏大形簇边界上的样本容易被错分到邻近的小簇中，文献［17］针对这一问题引入了聚类准则函数和加权距离进行改进。本文将该方法引入到K 中心点算法的第3 步，从而提高对边界样本的聚类精度。

聚类准则函数以加权簇内标准差之和最小化为目标，在每次迭代时根据聚类准则函数大小将数据点分配到相应的簇中。设样本总量为M，第i个簇中样本个数为mi，第i个簇的标准差为σi，则聚类准则函数定义如式（1）所示。

加权距离计算公式如式（2）所示。

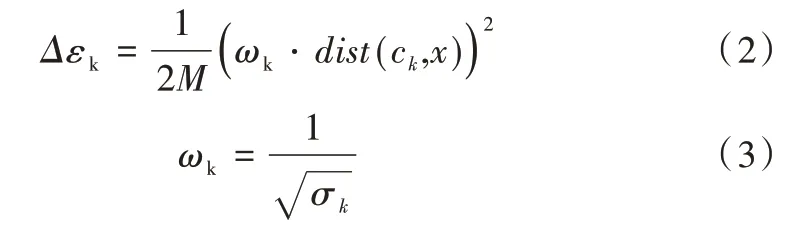
其中，dist(ck,x)表示簇中数据点x到中心点ck的距离，ωk表示样本权重，式（3）使得密集簇的权重更高，从而使划分结果更加靠近簇中心点，聚类结果变得紧凑。

2 不平衡数据下的K 值寻优

2.1 ET-SSE 算法

最佳K 值的选择对于聚类结果有着很大影响，为判定最优K 值，文献［18］提出了ET-SSE 算法，通过引入指数函数放大正值影响并在簇内误差平方和的基础上提出了新的度量方式，以提高度量效果。ET-SSE 的计算公式如式（4）所示。

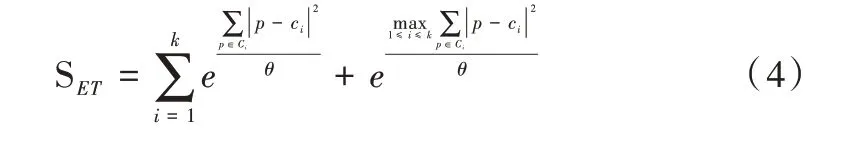
其中，θ为权重，可调节SSE 的大小，Ci表示第i个簇的中心点，p为第i个簇中的样本对象。

2.2 UET-SSE 算法

不同于ET-SSE 的是，在聚类过采样算法中，聚类算法仅仅作为预处理步骤，其目的是通过聚类发现规则相似的样本，为接下来的样本合成步骤提供参考，因此聚类的目标不是区分两类样本，而是将相似度高的样本进行归纳。因此，本文提出了应用于非平衡数据的K 值选取方法UETSSE，它通过计算每个簇内的多数类样本中心距离与少数类样本中心距离的平均比值确定最优K 值，计算公式如式（5）所示。

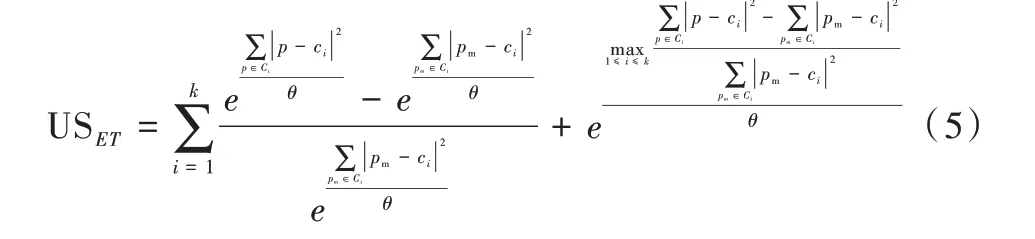
其中，Ci表示第i个簇的中心点，p为第i个簇中的样本，pm为第i个簇中的少数类样本。式（5）中第一项的分子是全体样本与少数类样本的中心距离差，分母为少数类样本的中心距离，第一项代表pm周围的多数类样本密度；第二项为偏执项，它取第一项结果中的最大值，用来放大差异。USET在计算USET后可以作图判断K 值凹点，以German数据集为例计算USET得分并作图，如图1 所示，USET随着K值增大不断上升，表明分簇越多样本越稀疏。当K=4 时形成一个明显的凹点（二阶导数大于0），因此最佳K 值为4。

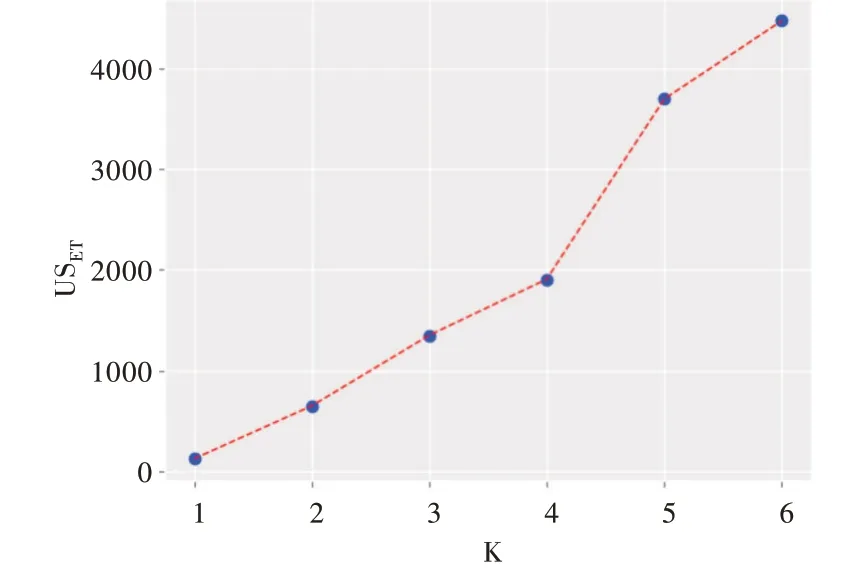
Fig.1 Optimal K-value judgment图1 最佳K 值判断

3 聚类过采样

3.1 边界阈值与区域划分

KmeansSMOTE 给予稀疏簇更高的采样权重，但是没有规定决策边界，容易过度关注远离类边界的稀疏样本，导致一些孤立点或边缘点被过度采样，而边界样本采样过少，具体如图2 所示。为划分适合聚类采样的区域，本文利用混叠样本对聚类区域进行划分，如图3 所示，内圈为样本混叠较多，适合深度聚类区分，外圈为稀疏区域，过大的欧式距离不适合进行聚类。

Fig.2 KmeansSMOTE sampling results图2 KmeansSMOTE 采样结果

Fig.3 Boundary thresholds and region demarcation图3 边界阈值与区域划分

边界阈值计算步骤如下：

（1）计算n个特征与标签的Pearson 相关系数r(fi,y)，得到集合P，将P 中绝对值最大的特征作为关键特征T。

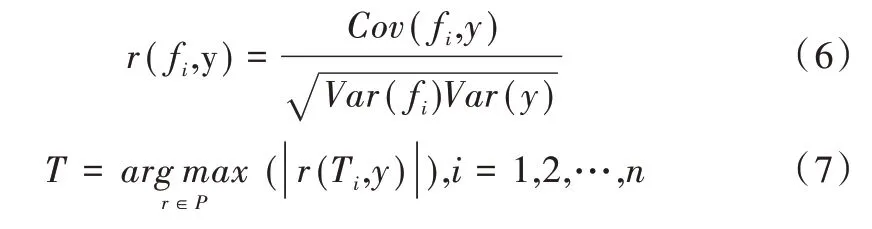
（2）计算少数类样本点Xi的K 近邻，设Xi的K 近邻中相反类别占比为θ，若0 <θ≤1/3，则将Xi视为边界支持点，加入集合E，若θ等于1 则作为噪声点剔除。

（3）计算集合E 中样本点在T 上的均值作为边界阈值，XT表示样本X 在T 上的值，将XT与比较并根据式（8）划分内圈和外圈。

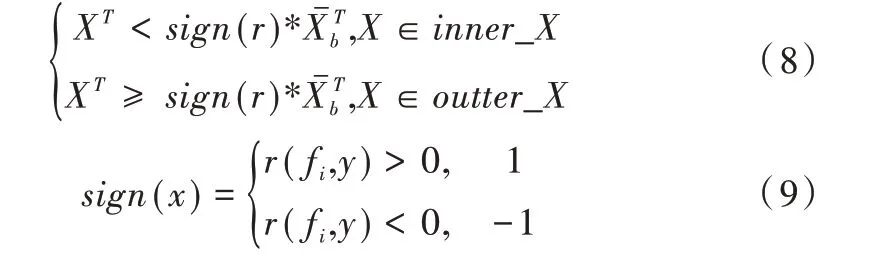
3.2 加权过采样

通常情况下，样本重要性取决于密集度和信息量，张家伟等［19］指出靠近类别中心和边界的样本生成权重应该更大；田臣等［20］认为边界样本和稀疏簇中的少数类样本采样权重更大。因此，本文在聚类时引入加权过采样策略，给予靠近簇中心样本更高的权重，具体步骤如下：

（1）通过K 中心点聚类得到K 个簇，对于每个簇C 中的少数类样本Xi，计算它到中心点的欧几里得距离Di，取中心距离的倒数作为Xi的采样权重。

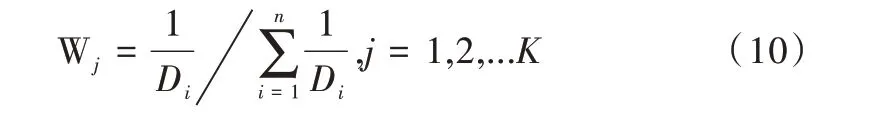
（2）根据采样倍率N 确定合成样本数目，对每一个少数类样本Xi，从其K 近邻中随机选择样本点Yj，并根据式（11）合成新样本。

（3）将新样本与原始数据集合并，得到新数据集。

4 KMediods-SMOTE

4.1 算法流程

KMediods-SMOTE 采样流程如图4 所示，为检验合成效果，本文在合成样本后输入分类模型，并使用三折交叉验证和网格搜索进行调参，最后验证分类结果。

4.2 算法描述

输入：不平衡数据集S，K近邻数n，簇最小保留阈值irt。

输出：合成的样本数据集。

Step1：将原始数据集分为训练集T和验证集V；

Step2：计算T 中所有少数类样本的K近邻，根据上文方法得到训练集X_train和边界点集合Xd；

Step3：计算需生成样本的总数量；

Fig.4 Algorithm flow图4 算法流程

Step4：根据边界阈值划分聚类区域与非聚类区域；

Step4.1：根据式（6）和式（7）计算边界阈值；

Step4.2：将小于边界阈值的样本划为内圈点，剩余的划为外圈点，分别记作inner_X和outter_X；

Step5：根据式（5）确定最优K 值，使用改进的K 中心点算法对内圈样本聚类，并将inner_X划分为K 个簇；

Step6：判断各簇内少数类样本数量是否大于irt，过滤掉较小的簇；

Step7：计算采样权重；

Step7.1：计算样本到簇中心点平均距离的倒数作为簇间采样权重；

Step7.2：根据式（10）计算簇内采样权重；

Step8：将边界支持点X_edge加入outterX，计算外圈点中少数类样本的K 近邻集合以供插值，并根据内圈和外圈中的样本数量分配合成数目；

Step9：分别对内圈点和外圈点过采样，得到合成后的新数据集new_X。

5 实验与分析

5.1 数据来源

实验选取了4 个信用风险数据集，由于Credit_card 类别极端不平衡，因此随机抽取2%的多数类样本与少数类样本混合组成新数据集，数据情况如表1 所示。

Table 1 Data description表1 数据描述

5.2 评价指标

实验使用混淆矩阵刻画分类效果，其定义如表2 所示。由于准确率无法准确评估不平衡数据的分类效果，因此实验选取前人使用较多的G-means和F-measure作为评价指标。式（15）中，β表示Recall和Precision的相对重要性，实验中通常取值为1。

Table 2 Credit risk assessment confusion matrix表2 信用风险评估混淆矩阵

5.3 实验设置与分析

实验使用Python3.7 实现本文算法，并与SMOTE、Bor⁃derlineSMOTE、KMeansSMOTE 进行比较，在参数调优后进行五折交叉验证。为检验各方法在集成分类模型下的效果，选择RF、Adaboost、logistics 3 种分类器进行试验，各分类器参数取值范围如表3所示，分类结果如表4和表5所示。

Table 3 Parameter range表3 参数取值范围

Table 5 F-measures of four kinds of oversampling methods in different classifiers表5 4 种过采样方法在不同分类器中的F-measure

可以看出，本文方法在RF 分类器下的指标全为最优，在天池竞赛商业银行数据上相比KmeansSMOTE 在Gmeans 和F-measure 上提升了1.18%和5.35%，在German 数据集上相比KmeansSMOTE 在G-means 上提升了2.03%。但在Credit_card 下的效果与KmeansSMOTE 差别不大，主要是因为Credit_card 数据集离散度和混叠度不高，边界样本比较集中。4 种方法中，KmediodsSMOT 表现良好，Kmeans⁃SMOTE 次之，BorderlineSMOTE 和SMOTE 表现最差。

6 结语

本文针对传统聚类过采样算法的边界样本损失问题，通过划分边界阈值和引入聚类准则函数改进了K 中心点算法，并提出一种适用于非平衡数据的K 值寻优方法。通过与较新的KMeansSMOTE 进行对比实验，表明该算法在非均衡数据集上性能较好，并有效地提高了少数类样本的分类精度。研究表明，缩小聚类区域和改进聚类准则函数可以提高对边界样本的采样权重，并避免了孤立点和极值点的干扰，从而在聚类过采样后得到了更好的分类效果。然而本文方法仍然存在一些不足：它并未考虑到数据集的混叠度和样本分布，因此后续研究有待引入分布函数以确定样本密集区域，并重点对边界样本集中区域使用本文方法，以提高聚类过采样效果。