大质量BTZ 黑洞的WCCC 验证

聂维福

（西华师范大学，四川 南充 637009）

众所周知，大质量天体在引力坍塌过程中会形成一个时空奇点，在时空奇点附近一切物理规律都将失效[1]。为了避免这种情况出现，Penrose 提出弱宇宙监督猜想（WCCC），猜想指出在引力坍塌产生奇点过程中，奇点必将隐藏在黑洞的事件视界之后[2]。猜想提出至今，对于猜想的证明一直是热门研究领域，经过最近几十年的研究得出了最有意义的有两种证明方法，第一种是Wald 设计的Gedanken 试验法[3]，第二种是测试标量场法。

第一种方法检验极端Kerr-Newman 黑洞时，Wald 发现极端黑洞是不能吸收带电粒子[3]。在近极端Reissner-Nordstom 黑洞和Kerr 黑洞检验中，研究人员发现WCCC 是违背的，研究中考虑带电粒子的能量、角动量、电荷等参数，导致用此方法研究极端Kerr-Newman 黑洞WCCC 都是违背的[4]。有研究人员认为这种方法是不准确的，因为没有考虑粒子本身因素，因此对于这种方法就存在一些争议[5]。最后考虑了所有可能的因素在验证中再对黑洞进行研究，发现WCCC 对极端黑洞和近极端黑洞都是有效的，对于非极端情况的黑洞也被证明可以满足WCCC[6]。在最近几年里，研究逐步向AdS 时空深入，研究人员通过Wald实验基本模型设计了“测试粒子法”用于验证AdS 时空中黑洞WCCC 的有效情况[7]。在这个时空中黑洞的质量被给了新的定义，表示黑洞的热力学焓，同时黑洞的宇宙学常数及其共轭量被认为是压强和体积，这个方法还可以用来讨论AdS 时空中黑洞的热力学性质[8]。最近几年研究人员用这个方法研究了高维RN-AdS 黑洞[7]、BL-AdS 黑洞、tour-like-AdS 黑洞、一般黑洞等等。

对于三维黑洞的研究，目前主要是研究黑洞的热力学和一般情况下的三维黑洞的WCCC[9]，对于大质量静态三维BTZ 黑洞主要集中在研究量子隧穿、P-V 临界、热力学方面[10]。在能动张量的基础上使用这个方法验证洛伦兹破缺情况下大质量BTZ黑洞在相空间中的WCCC 有效性，在研究讨论中将大质量参数赋值得出了符合预期的结果。

1 大质量BTZ 黑洞的引力理论

首先，定义大质量参数ci和d×d 矩阵Kμν=（gμаfаν）1/2的特征值的对称多项式U，其中[K]=Kμμ，（A1/2）μν（A1/2）νλ=Aνλ。含有交换规范场U 和负宇宙常数的大质量BTZ 黑洞[11]的作用量为：

式中L（Γ）是矢量规范场的拉格朗日量，Λ 是宇宙常数，R是曲率标量，M^2是黑洞质量参数，f 是稳定的对称张量，Γ=FμνFμν是麦克斯韦不变量。设度规方程为：

其中，f（r）是场方程径向函数。通过考虑与径向电场相关的规范势Aμ=f（r）δtμ，并按照文献[13]中的方法，能得到（2）式f（r）的具体表述：

式中m=8M 和q=2Q，M 和Q 表示黑洞的质量和电荷量。宇宙常数Λ=-1/l2。大质量情况下的BTZ 黑洞，利用引文献[12]的方法（3）式可以简化为：

2 大质量BTZ 黑洞吸收带电粒子的能量-动量关系

使用Hamilton-Jacobi 方程来计算大质量BTZ 黑洞获得一个带电粒子在事件视界附件的能量-动量关系[13]：

其中p=аμI 是动量，e 是电荷量，m 是黑洞质量，I 是带电粒子的Hamilton 作用量。在球对称时空中，带电粒子的Hamilton 作用量可以从（12）分离得到：

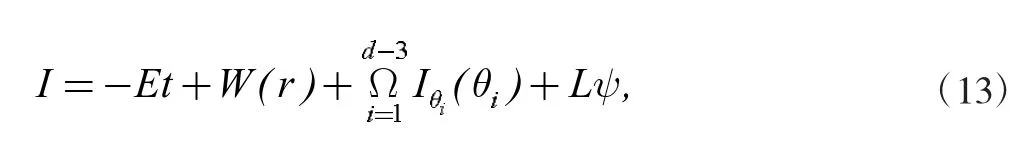
式中E 是带电粒子的能量，L 是带电粒子的角动量，W（r）和Iθi（θi）分别是方程（13）的径向和角向分量。经过对径向方程计算，化简能得到径向动量为：

当带电粒子被黑洞吸收时，在视界附近有f（r+）=0。则（14）式可以简化为：

其中pr+=pr（r+）。对于│pr+│项，规定它为正值，以保证粒子在顺时间方向落入黑洞。

3 大质量BTZ 黑洞的WCCC 验证

在正常相空间中，大质量BTZ 黑洞的状态参数是黑洞的质量M 和电荷量Q。当带电粒子被黑洞吸收后，黑洞的状态参数将变为M+dM 和Q+dQ，事件视界r+和径向坐标rmin将变为r++dr+和rmin+drmin[14]。当极值点在rmin和rmin+drmin之间时，下式是满足的：

当r=rmin+drmin时，方程f（rmin+drmin）能被表示为：

这个值恒为负值，然而此时黑洞为极端黑洞，则pr满足pr=0，所以dfmin=0，意味着带电粒子落入极端大质量BTZ 黑洞时，黑洞还是维持极端黑洞状态。

对于近极端的大质量BTZ 黑洞，在r+=rmin+x 点将（15）展开，即：

对于上式，O[x]2是一个极小量，所以这项可以略去，第一项的绝对值比第二项大，等式符号由第一项决定，即dfmin<0。当带电粒子被黑洞吸收时，WCCC 有效。

在扩展相空间情况下，黑洞的状态参数有M，Q，l，黑洞吸收带电粒子后的状态参数变为M+dM,Q+dQ,l+dl。相应的最终状态下的视界半径和最小极值点为r++dr+和rmin+drmin。当r=rmin+drmin时，总是有如下关系：

这个值恒为负值，此时黑洞为极端黑洞，则pr满足pr=0，所以dfmin=0，意味着带电粒子落入极端大质量BTZ 黑洞时，黑洞还是维持极端黑洞状态，此时WCCC 有效。

对近极端黑洞，利用r+=rmin+x 关系在最小点附近展开到一阶形式，即：

将式子（26）代入（24）得：

有学者指出此时dfmin 可以忽略，因为它等于0，但注意到Θ 是一个极小量，不能忽视O[x]2对函数f（rmin+drmin）的影响[14]。f（r+）在rmin有：

上式值由L,Q,c,ci,M^2决定，当改变L,Q,c,ci,M^2的其中一个的值，F 方程会得到不同的结果。此时WCCC 不能确定是否违背。

4 结论

研究了三维静态大质量BTZ 黑洞的WCCC，在研究处理中对于大质量参数M^2，c，c1均是取特殊值研究，这是研究的不足之处，因而导致最后在研究扩展相空间WCCC 时，对于近极端黑洞情况无法得出准确值。