二阶广义全变分耦合非局部变换域模型的图像放大*

海 涛 ，鲍宜帆 ，潘浩浩

(1.南阳师范学院 机电工程学院，河南 南阳 473061；2.河南省毫米波无线通信射频前端及天线工程研究中心，河南 南阳 473061；3.河南省车辆零部件智能制造工程研究中心，河南 南阳 473061；4.南京理工大学 光电学院，江苏 南京 210094；5.南阳农业职业学院，河南 南阳 473061)

0 引言

图像放大实现了单幅图像分辨率增强，在图像处理中有广泛应用。利用全变分TV 模型(Total Variation，TV)对图像进行放大[1]，在图像边缘处理上有较好的处理效果，在平滑图像存在阶梯效应的不足。Bredies 提出了广义全变分(Total Generalized Variation，TGV)，是对全变分模型扩展的新模型[2]，解决了图像在平滑区域的阶梯效应，可以逼近高阶多项式，并且具备下半连续性，凸性和旋转不变性。TGV 在图像放大中得到应用，并取得了较好的效果[3]。

TGV 虽然较好地避免了阶梯效应，但是在弱边缘和细节部分处理效果提升并不大[4]。文献[5]采用TGV 和剪切波相结合的方法改善弱边缘和细节的增强；文献[6]提出了加权TGV 模型用于图像放大，增强其对弱边缘和细节的处理效果，通过非局部广义全变分实现对光流图形进行处理，很好地解决了弱边缘和细节处理效果。本文通过实现TGV 与非局部变换模型相结合的方法实现对图像弱边缘和细节的分辨率增强。

1 非局部变换域模型

文献[7]提出了三维块匹配(Block-Matching and 3D filtering，BM3D)算法，BM3D 是一种非局部思想在变换域实现的一种处理方法，其基本思想基于图像中存在相似的图像块，通过寻找相似的图像块，集合成一个三维的数据组，由于图像块的之间的相似性，三维的数据在变换域是一个稀疏的分解，利用这种稀疏性进行处理。

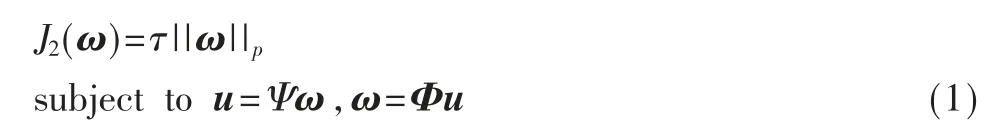
其中，Φ=Φ3DPJ，Ψ=WΨ3D。

2 基于TGV 耦合非局部变换域模型的图像放大

TGV 模型改进了全变分模型的阶梯效应，保留了图像一阶线性结构，但并未完全解决偏微分方程恢复纹理及弱边缘存在的不足，非局部变换域利用图像的全局信息，能够较好地恢复自然图像中纹理和弱边缘，本文提出一种广义二阶全变分自适应耦合非局部变换域模型的图像放大算法。

2.1 低分辨率图像获取模型

文献[9]给出图像的离散的退化模型如式(2)所示：

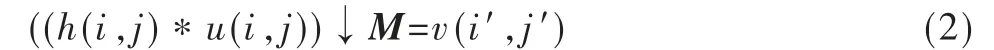
其中，h(i，j)是图像获取硬件的点扩散函数，为低通滤波器；*为卷积运算；↓M 为下采样矩阵；u(i，j)为理想的高分辨率图像，而v(i′，j′)为当前的低分辨率图像。各项以字典排序方法转换为矩阵表示法：u(i，j)用u 表示，v(i′，j′)用v 表示，H 表示包涵下采样操作的h(i，j)，可得到模型的矩阵表示：v=Hu。

由式(2)可得到基于图像获取模型的约束能量函数：

2.2 TGV 耦合非局部变换域的图像放大模型

TGV 模型在图像边缘有较好的实现并且能够去除平滑图像的阶梯效应，非局部变换域模型能够较好重建细节和弱边缘，综合其优点，得到本文放大模型。偏微分方程的变分模型优点之一是能够很容易实现和其他模型的耦合，具体实现方法是TGV 作为惩罚项直接加入非局部变换域变分模型式(2)，同时增加图像获取的约束能量函数，可以得到本文提出算法的实现模型如式(4)：

取k=2 得到二阶TGV 模型，得到式(5)：

最小化J(u，ω)得到放大图像u 为模型式(5)的最优解：(u*，ω*)=minJ(u，ω)。

2.3 TGV 耦合非局部变换域的图像放大模型实现

式（5）中，两个约束项u=Ψω 和ω=Φu 是一对可逆的正交变换对，对两个变量去耦合并除去其常量项可得：

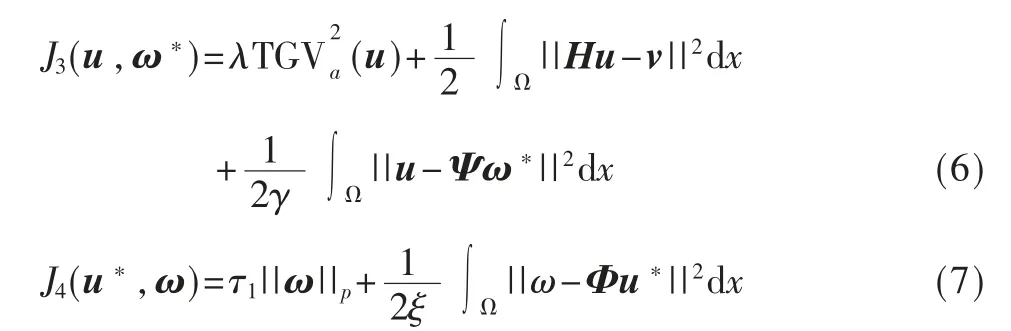
可以看出式(6)为受约束的二阶TGV 模型，实现对图像的锐化操作，而式(7)为p 阶非局部变换域模型，本文取p=1 为图像的去噪操作。

本文放大模型实现通过逐次逼近方法求解式(6)和式(7)最优化解即可求得放大模型(5)的鞍点，进而得到高分辨率图像。

2.3.1 受约束的二阶TGV 模型实现

式(6)中第二项为退化模型式(3)的约束项，考虑采用文献[10]提出的拉普拉斯框架下采用双正交滤波器实现可逆重建，如图1 所示。

图1 拉普拉斯重建

公式实现如式(8)所示：

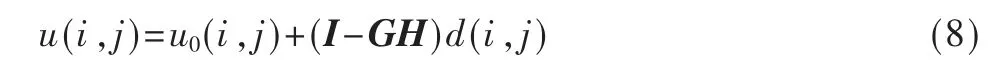
其中，d(i，j)为锐化后图像与初始图像相比图像增加的细节和边缘部分。对正则化处理后的图像求出d(i，j)，代入式(8)，求出的新图像完全满足约束模型式(3)。

式(6)的求解可以转化为在式(8)拉普拉斯双正交重建框架下求解式(9)的最优解。

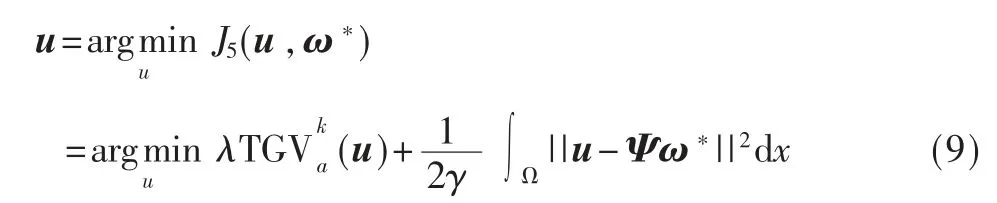
采用文献[11]一阶原始-对偶算法实现式(9)的最优化求解如下：

2.3.2 一阶非局部变换域模型实现

一阶非局部变换域模型即式(7)p=1 的实现采用文献[13]的变换域硬阈值法求解，即：

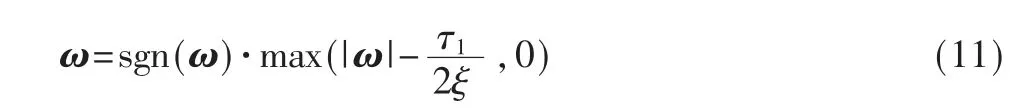
迭代实现为：

2.3.3 本文模型的实现

本文采用逐次逼近方法求解式(6)和式(7)最优化解即可求得放大模型(5)的鞍点，得到高分辨率图像。

具体实现过程如下：

输入：v(低分辨率图像)；h(设备退化函数)。

初始化：确定h →g，Φ，Ψ，u0=(v(i′，j′)↑M)*g(i，j)=Gv，ω0=Φu0，t=0，θ←0，θ¯←0，u¯←u0，p←0，q←0，δ＞0，τ＞0。重复以下操作：

(1)锐化：

①迭代实现式(10)；

②拉普拉斯双正交重建：

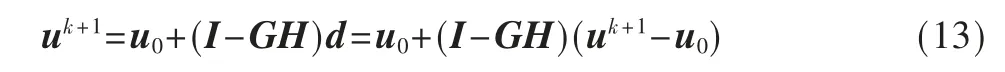
(2)去噪声：

直到uk+1-uk＜ε，结束迭代；否则，继续从步骤(1)开始。

3 仿真实验结果及比较

实验设计如下：给定高分辨率图像(标准图像)如图2所示，利用给出的低通滤波器h 低通滤波后下采样，得到退化图像如式(3)所示，进行按给定倍数进行分辨率增强。与给定的高分辨率图像进行比较，比较主观视觉效果，相应的峰值信噪比(Peak Signal to Noise Ratio，PSNR)和平均结构相似性测度(Mean Structural Similarity Measure，MSSIM)用户验证算法放大效果[14]。

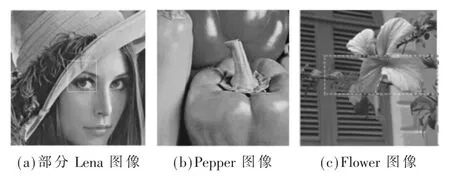
图2 仿真图像

实验参数设置如下，4 倍放大时(纵向2 倍放大，横向2 倍放大)，根据文献[2]正则化参数λ 约为正则化参数τ1的1/6，本文正则化参数选择为λ=0.001 7，τ1=0.008 7，γ=0.000 55，ξ=1；TGV 正则化求解参数选择为δ=τ=1/3，α1=1，α0=4。h(i，j)滤波器由一维滤波器h(i)=(0.5，1，0.5)张量积扩展得到，对应的g(i，j)由一维滤波器g(i)=(-1/8，2/8，6/8，2/8，-1/8)通过张量积扩展得到。16 倍放大由两个4 倍放大串联实现。

为验证算法的有效性，选择以下算法进行比较：文献[3]的基于小波变换的TGV 图像放大算法、文献[15]的基于BM3D 进行放大的算法(简称为BM3D 算法)、文献[16]的TV 耦合非局部均值滤波器(简称TV-NLF)算法、文献[17]的改进的复扩散耦合非局部均值滤波器(简称ICF-NLF)算法，后两种算法都运用局部的偏微分方程耦合非均值滤波器实现放大，所有比较算法均采用文献中最佳参数。

图3 为Lena 图像白色方框4 倍放大实现，在原始图像图3(a)中的黑框位，TV-NLF 算法(即图3(d))存在一定的阶梯效应，其他图像效果要好一些；TGV 图像虽然在图像中帽檐的强边缘有较好的锯齿波，但是存在一定弯曲。图3(c)BM3D 算法边缘存在模糊现象，本文算法在边缘有较好效果,主要原因是TGV 耦合了非局部变换域模型较好地去除了边缘的震荡引起的扭曲，在眼睫毛处也有较好的细节小边缘处理效果。

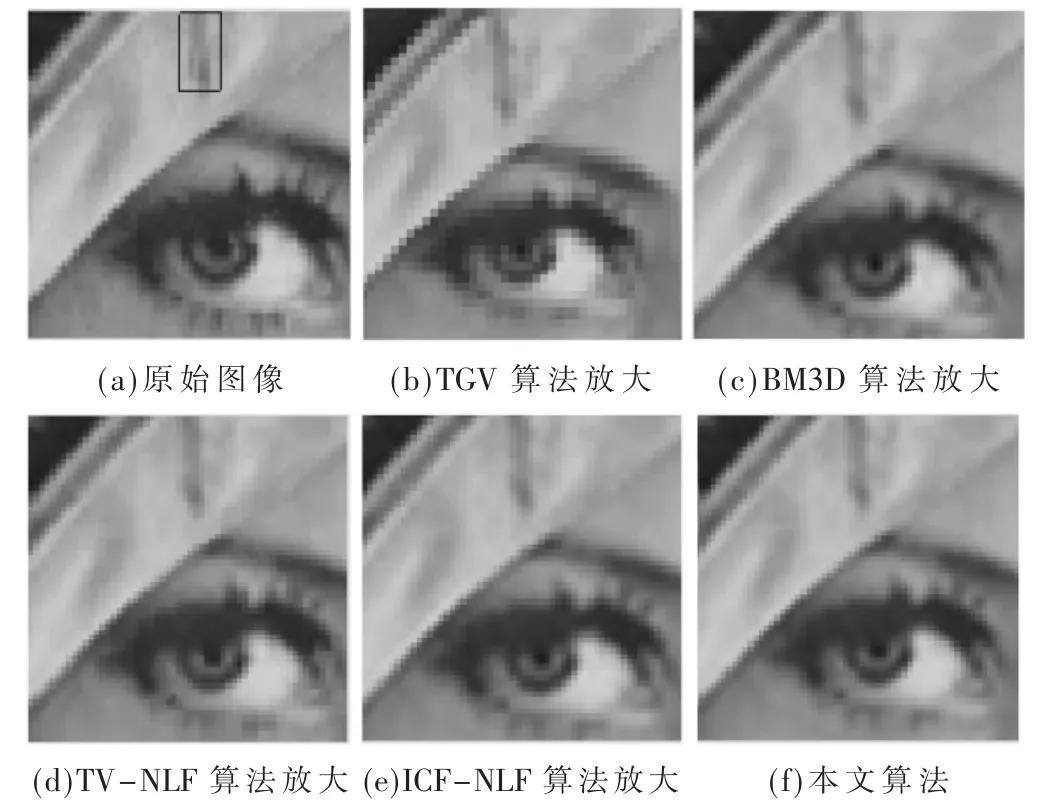
图3 4 倍放大部分Lena 图像

图4～图6 为仿真图像16 倍放大图像。由图5 的帽檐纹理和头发可以看出，本文算法较好地保留了小边缘和纹理细节，相对于TGV 算法，帽子上部的纹理和小边缘效果更好，达到其他采用非局部方法处理的效果；BM3D 算法中的强边缘效果较差，存在较大锯齿波，其他采用二阶微分方程的算法不存在这一问题。由图5 的Pepper 的柄可以看出，本文算法锯齿波效应较小，其他算法存在不同程度的锯齿波。图6 同样显示了本文算法弱小边缘的纹理效果最好，可由图7 的部分放大图像得到进一步验证。

图4 16 倍放大Lena 图像

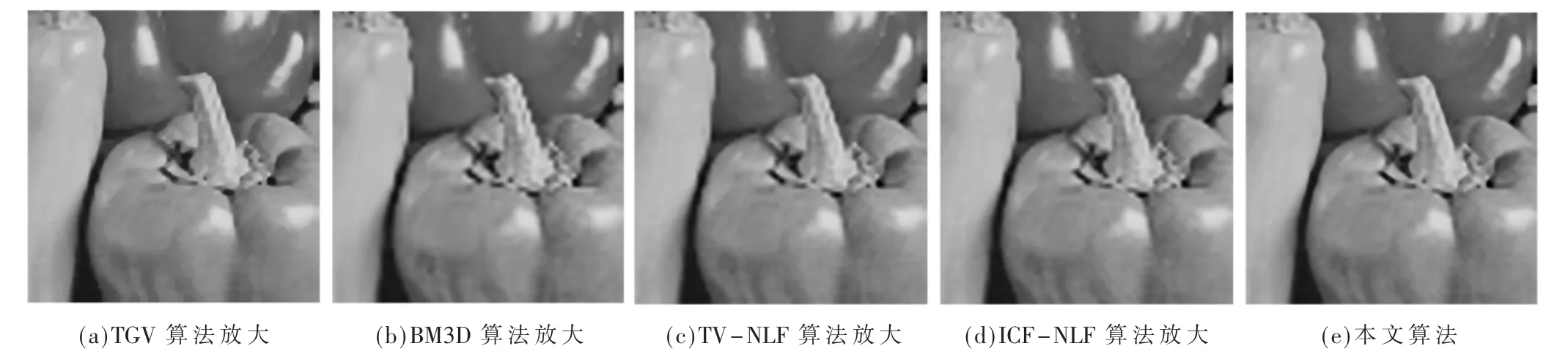
图5 16 倍放大Pepper 图像

图6 16 倍放大Flower 图像

由图7 图像可以看出，本文算法在页面的纹理细节方面达到了TV-NLF 算法放大、CF-NLF 算法放大和BM3D 算法良好水平，同时优于TGV 算法，本文算法在花蕊柄的边缘效果更好。放大实验结果PSNR 和MSSIM如表1 所示，本文算法在PSNR 和MSSIM 都有最好的仿真结果。

表1 仿真图像PSNR 和MSSIM

图7 16 倍放大部分Flower 图像

4 结论

本文提出了一种基于TGV 耦合非局部变换域模型的图像放大算法，该算法能够较好地利用TGV 模型和非局部变换域模型的优点，得到了较好的放大效果。仿真实验证明，本文算法改进了TGV 算法小边缘和细节处理能力不足的缺点，同时避免了非局部变换域在强边缘部分的放大处理锯齿波明显的不足，具有较好的视觉效果。与其他放大算法进行比较，PSNR 和MSSIM 也取得了较好数值，进一步证明本文提出算法具有较好的性能。进一步优化算法中的各个参数，以便实现全局信息和局部信息的最佳耦合是该算法下一步努力的方向。