基于模拟退火模型运输路径网优化研究

庄梦婷

安徽财经大学统计与应用数学学院，中国·安徽 蚌埠 233030

1 引言

同城配送存在路径迂回问题，所谓迂回运输就是没有从最短的路线运输，而是绕道运输的形式，如因到达地区顺序不同而导致的总路径变长。物流公司不能以最近的公路运输，将会直接影响公司的运输效率降低，也会导致不必要的运输成本增加[1]。而道路迂回问题是在很多物流配送过程中存在的问题。

配送车辆承载量的约束条件：每辆货车都存在其重量承载量以及体积承载量，考虑到承载量的问题，每辆货车所承载的货物有限。综合考虑不同城区物流件数之间存在的差异，派送车辆数量成为一个问题。时间约束因素包括即物流配送过程货物有要求到达时间、大部分同城运输都要求在当天完成货物配送，其他因素包括路段时速限制、堵车的可能性、天气限速。

2 研究设计

2.1 基于模拟退火模型的单式运输路径优化

针对起点到终点只有一种运输方式可供选择，即直达的情况，我们拟建立模拟退火模型从运输路径角度进行优化；综合考虑车的承载量以及不同地区订单数存在的差异的问题，利用聚类分析，将地区进行分类，在不同地区上利用模拟退火算法进行不同区域的最短路径计算。具体包括：发货点和收货点的设置；规划适当的路线；使运输车辆能够有序地通过计划中的地点以及完成货物的需求量和发货量，并且满足交货时间，即达到实现最短时间内；最短运输成本下完成相应的目标，去掉在路上的“浪费”[2]。

2.2 研究方法：模拟退火算法

模拟退火是一种通用概率算法，用来在一个大的搜寻空间内找寻命题的最优解。其来源于固体退火原理，将固体加温至充分高，再让其徐徐冷却。加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小[3]。对于地点之间的转移概率矩阵两两相互之间是互通的，即可得出该转移矩阵对应的有限的马尔科夫链是收敛的。收敛说明过程将达到平衡状态，即此后过程取某一个状态的概率不随时间变化[4]。

①解空间S表示为{2,3, ,}n,1 … 的所有起点和终点的循环排列集合，即：

其中，每一个循环排列表示运输完n个运输点的一个回路，πi=m 表示在第i-1次运输目标m，初始解可选为(1 , 2,3,…, n)，这里使用蒙特卡洛法求得一个比较好的初始解。

②目标函数：目标函数为一次走过所有运输点的路径长度，即：

③新解的产生。设上一步迭代的解为：

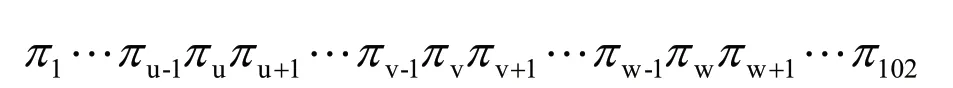
应用变换法时，任选序号u,v交换u和v之间的顺序，变成逆序，此时的新路径为：

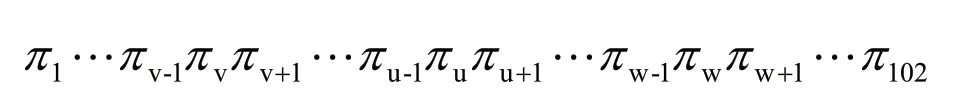
④代价函数差：对于2变换法，路径差可表示为：

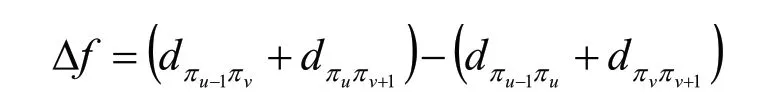
⑤接受准则：

⑥降温：利用选定的降温系数α进行降温，取新的温度T为αT（这里T为上一步迭代的温度），这里选定α = 0.999。

⑦结束条件：用选定的终止温度e = 10-30，判断退火过 程是否结束。若T＜e，则算法结束，输出当前状态[5]。

求解过程如模拟退火流程图1所示。

图1 模拟退火流程图

2.3 数据的搜集和处理

由案例以及网上搜索可得到中国北京市某次单运输方式任务的物流采购点以及产品运输点，并将中国北京市需要运输的运输点以坐标点的形式写在一个平面上。

根据上述流程图，我们为空间设计了LINGO自动诊断的代码，只要将某次需要向外运输或者采购原材料的运输点坐标数据输入并在程序中加入循环语句，运行出运行结果，得到最短运输路径。这条运输路径能保证运输人员在无一运输点遗漏的情况下，所走的运输路径最短，也就是说此时达到了路径的优化。

3 算例分析

为了更好地体现模拟退火模型在单一运输方式上的运输效果，我们以中国北京市某次运输案例为例，运用模拟退火模型对路径进行优化设计。选取中国北京市为例，提货区为朝阳区，剩余地区为所需配送地区。

距离矩阵如下表1所示。

表1 北京市各区距离矩阵

3.1 单一式配送

在不考虑订单量的约束条件下，货物从起点出发，送达各目的地对应的编号如表2所示[6]。

表2 地区编号

目标函数为寻找从点出发，遍历中间点，返回n的最短路径。在计算机上运行以上程序，总运输距离为462km，运输路径为1-15-14-3-2-7-6-8-16-13-5-12-11-10-4-9，表明从朝阳区出发，经过东城区、西城区、海淀区、丰台区、大兴区、房山区、石景山区、门头沟区、延庆区、昌平区、怀柔区、密云区、平谷区、顺义区，最终回到通州区。

3.2 多车配送

考虑到订单量的情况下，将中国北京市16各地区首先要根据地理位置进行分类，再结合订单多、少相互配合，聚类图如下图2所示[7]。

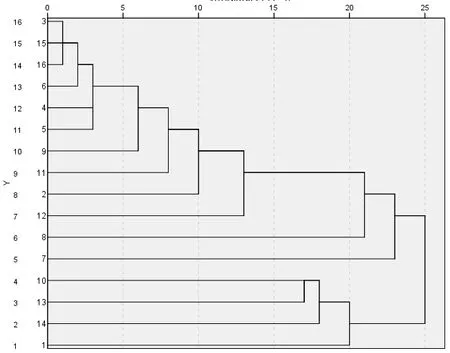
图2 聚类结果图

将地区分为三类：

第一类为顺义区、平谷区、密云区、柔怀区、昌平区、延庆区，这些地区中，顺义区订单最多，其余地区订单较少，恰好满足货车的承载量需求。

第二类为在满足货车承载量的前提下订单量较多的通州区和大兴区。

第三类为东城区，西城区、海淀区订单较多和门头沟区和房山区订单较少的地区组成。重复上述计算过程，得出每个区的最短路径和总路径。

结果显示，第一类的路径为朝阳区、顺义区、平谷区、密云区、柔怀区、昌平区、延庆区，最终回到朝阳区，路径长度为333km。第二类路径为从朝阳区出发，先结果通州区，再到大兴区，最后回到朝阳区，路径长度为98km。第三类路径为朝阳区、东城区、海淀区、石景山区、门头沟区、房山区、丰台区、西城区，最后回到朝阳区，该路径长度为127km。三类区域总路径为558km。

4 结语

由算例分析，我们可以发现模拟退火算法的优点和在应用中进行推广的原因：

①在用模拟退火模型处理最短路径问题的时候，编程工作量少，且易于实现，统计上可以保证找到全局最优解。

②模拟退火算法是一种新的随机搜索方法，适合于解决大规模组合优化问题的通用而有效的近似算法。因此，也适用于论文中的运输优化问题。

③与以往的近似算法相比,模拟退火算法具有描述简单、使用灵活、运用广泛、运行效率高和较少受到初始条件约束等优点。

④模拟退火在找到最优解时需要花费非常多的时间，当冷却速度过快时，会导致模拟退火无法找到最优解，但速度过慢，又会导致运行时间变长。

此模型可以对各类运输问题的路径进行优化，只要将运输点数量输入程序和将运输点变换为坐标格式，就能得到一次性走过各点的最短路径，避免了重复走在运输上的“浪费”，这也是基于节能减排理念的一种物流优化。利用此方法，可以将很多交通以及其他方面的交通运输问题达到路径最优化，从而实现高效的交通运输速度。