基于匹配滤波和多特征融合的羊绒羊毛纤维识别

朱耀麟，穆婉婉，李云红，武 桐

(1.西安工程大学 电子信息学院，陕西 西安 710048； 2.西北工业大学 电子信息学院，陕西 西安 710072)

羊绒因其独特的手感和保暖性，常常被用作高档服饰的原料，深受消费者喜爱。由于羊毛在外观形态、化学结构和物理性质等方面都与羊绒极其相似[1]，所以市场上使用羊毛掺混羊绒的现象非常普遍，但二者价格和服用性能都相差巨大，因此，建立客观、准确的羊绒羊毛纤维自动识别模型具有重要的现实意义。

目前常用的羊绒和羊毛纤维识别方法有显微镜检测法[2]、近红外光谱法[3]、DNA检测法[4]、基于图像处理与计算机视觉的方法。其中，基于图像处理与计算机视觉的方法成本低，易于实现，是目前纤维识别领域的研究热点[5-6]，这种方法的关键是对纤维图像的处理和特征的提取。沈精虎等[7]对羊绒羊毛纤维扫描电子显微镜(scanning electron microscope，SEM)图像通过边缘检测、二值化、膨胀腐蚀等操作提取纤维骨架，接着对损伤、杂质等部分进行人工处理，选取纤维直径、鳞片厚度、鳞片边缘倾斜率等11个特征指标进行区分。石先军等[8]将阈值分割与边缘检测结合以分割纤维骨架，测量其18个几何指标并进行分析，遴选出最优组合，通过贝叶斯模型对羊绒羊毛进行识别。上述方法都直接使用边缘检测算子提取纤维骨架，只适用于对比度较好的图像，易受光照、噪声的影响，结合其他算法进行处理，增加了时间复杂度和空间复杂度，且都依据纤维几何特征进行分类，但几何特征对数据的敏感程度高，近年来羊绒“羊毛化”现象严重，这种方法很难再满足要求。柴新玉等[9]提取了纤维的加速稳健特征(speeded up robust features，SURF)进行聚类，将特征转换成对应的高维向量，借助支持向量机(support vector machines，SVM)对纤维进行分类。刘伟丽[10]采用局部二值模式(local binary pattern，LBP)特征将纤维图像转换成二进制序列，统计编码的直方图向量送入SVM进行识别。焦明艳[11]使用灰度共生矩阵(gray-level co-occurrence matrix，GLCM)来描述图像纹理，并从中提取了5个二次统计量作为特征参数进行分析。单一纹理不能完全表征羊绒羊毛纤维图像信息，导致识别率不高。

依据以上分析，本文提出一种基于匹配滤波和多特征融合的羊绒羊毛纤维识别方法。该方法针对羊绒羊毛纤维SEM图像的特点，设计合适的滤波核函数以提取纤维骨架，依据纤维骨架图像信息的不同提取其几何特征、纹理特征、边缘特征，融合成多维向量送入SVM对羊绒与羊毛纤维图像进行分类。

1 系统模型

通过研究发现，图像处理技术区分羊绒羊毛纤维的主要依据在于二者的表面形态和鳞片结构不同。羊绒纤维直径较小，鳞片表面较为平滑，而羊毛纤维相比而言更粗，鳞片间隔小、密度大，且排列不规则。这些信息主要集中在纤维骨架部分，即在羊绒羊毛纤维图像识别中，纤维边缘及鳞片边缘起决定性作用。

依据2种纤维鳞片模式的不同进行分类，图1给出了本文算法的主要流程。输入图像首先经过预处理去除背景，使得提取的特征都能集中在纤维主体部分；其次经过匹配滤波分割纤维骨架，便于提取纤维边缘和鳞片边缘信息；然后通过灰度直方图统计特征表征纤维鳞片密度，GLCM特征表征纤维鳞片均匀度，方向梯度直方图(histogram of oriented gradient，HOG)特征表征纤维轮廓和形状，获得羊绒羊毛纤维图像完善的特征信息；最后将特征进行融合后送入SVM分类器。

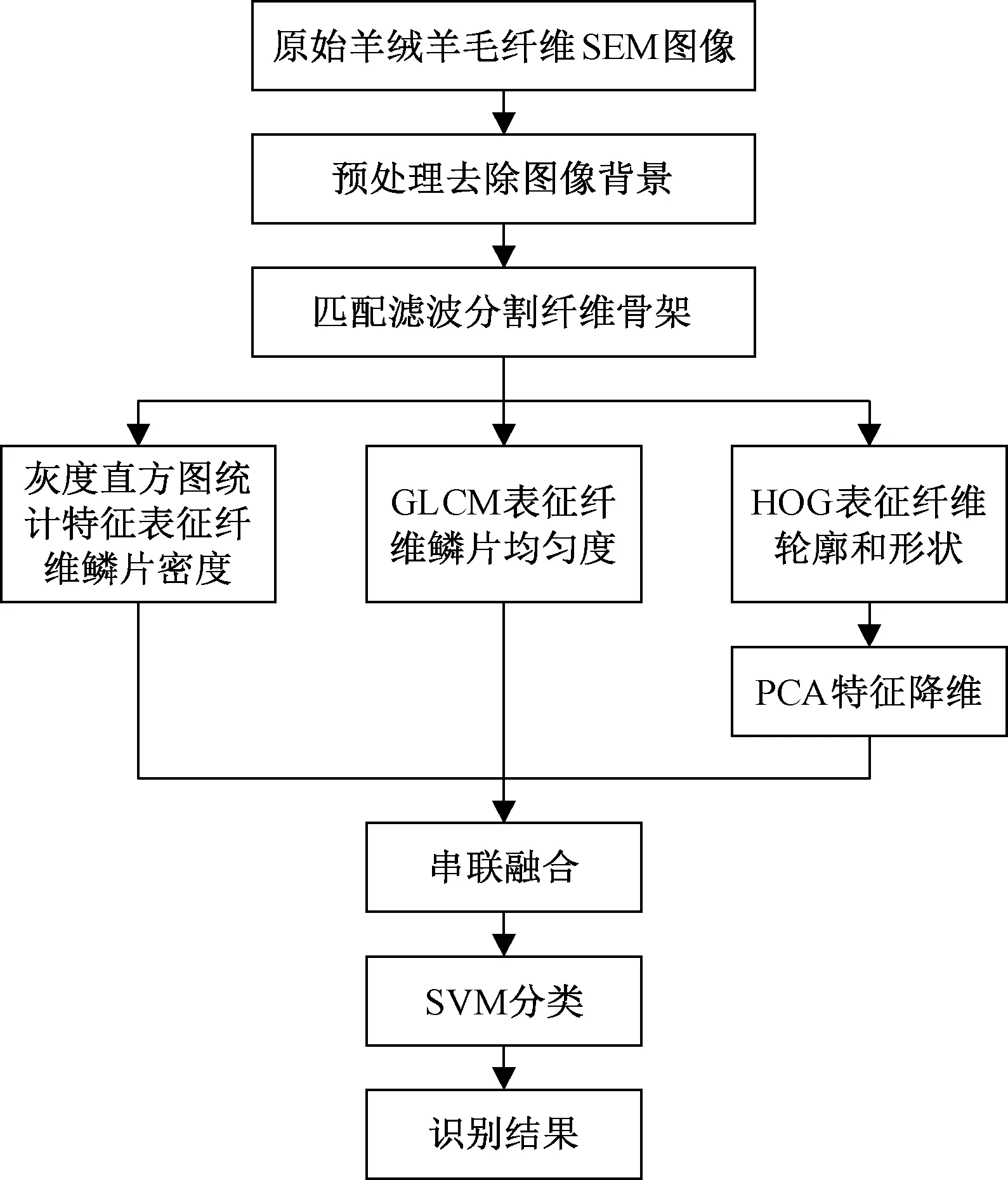
图1 算法流程图

2 基于匹配滤波和多特征融合方法

2.1 匹配滤波法分割纤维骨架

匹配滤波器是指滤波器的性能与信号特性达到一致，使得输出信号有用成分最强，噪声成分最小，即输出信噪比最大。本文采用匹配滤波[12]的方式分割纤维骨架。

图2为截取的一段纤维SEM图像鳞片边缘横截面及其周围像素的灰度分布图，横坐标为截取片段像素值，纵坐标为像素的灰度值。由图可知，鳞片边缘横截面灰度值高，周围像素灰度值低，符合高斯分布。观察纤维图像可以看出羊绒羊毛纤维具有以下特点：①鳞片边缘具有较小的曲率，可以用分段线性段表示。②鳞片边缘的细度在小范围内变化，可基本视为不变。③图像亮度不匀，传统方法无法准确提取纤维轮廓。基于以上特点，本文使用高斯曲线来拟合鳞片边缘横截面及其周围像素的灰度变化，设计用于检测鳞片边缘和纤维边缘的滤波器。将纤维鳞片看做是一段一段相连的线段，在一定长度范围内，如果各鳞片边缘段宽度与高斯曲线尺度相匹配，就会产生较强的输出响应，从而识别鳞片边缘。因此滤波使用的二维高斯核函数定义为：

图2 纤维鳞片横截面灰度分布

K(x,y)=exp(-x2/2σ2),|y|≤L/2

(1)

式中：σ是高斯函数的尺度大小即鳞片边缘宽度，L代表分段鳞片的长度，大小均以像素衡量。

纤维鳞片边缘的方向是任意的，为了匹配不同方向的鳞片边缘，需要将高斯核矩阵旋转不同的角度。旋转矩阵为：

(2)

由于高斯曲线沿x轴方向无线延长，又因3倍标准差(σ)的尺度包含了99%的信息，对其进行截断，则第i个高斯核矩阵中的系数为：

ki(x,y)=exp(-u2/2σ2),∀pi∈N

(3)

式中：N={[u,v]||u|≤3σ,|v|≤L/2}。为了不改变纤维图像均匀背景区域的灰度特性，需要将高斯核减去其均值使其平均值为零，则匹配滤波高斯核矩阵系数为：

(4)

式中：A为域N的点数。

当滤波输出大小超过某个阈值T，则将该点标记为鳞片边缘的一部分，达到获取纤维骨架的目的。上述过程减小了非理想环境下错误检测纤维边缘和鳞片边缘的可能性，同时其可以显著抑制噪声引起的响应。

2.2 骨架图像特征参数提取

2.2.1 几何特征

本文通过统计纤维骨架图中黑色像素占全部像素的比例P作为纤维图像的灰度直方图统计特征，计算公式如下：

(5)

式中：p为黑色像素个数，图像大小为M像素×N像素。该特征在一定程度上反映了纤维鳞片密度，一般地，羊绒鳞片密度范围为57～64个/mm，羊毛鳞片密度范围为80～110个/mm[13]，对应的羊绒纤维黑色像素占全部像素的比例比羊毛纤维黑色像素占全部像素的比例要小。

2.2.2 纹理特征

对比羊绒羊毛纤维骨架图像发现羊毛纤维纹理相对复杂，这是由于羊绒鳞片多为规则的环状分布，间距较为均匀，周期性更强。Haralick等[14]提出，用来评估图像纹理粗糙程度，适宜提取纤维纹理特征。该方法通过统计图像中指定距离和方向的2个灰度值组成的像素对出现的概率，来表征图像像素的分布规律。

本文采用能量、相关性、熵、方差和4个二次统计量来描述纤维骨架图像的纹理特征。①能量：体现了图像灰度分布均匀性，羊绒纤维鳞片分布规律性更强，其能量更大。②相关性：用来衡量图像灰度在水平或垂直方向的相似度，图像局部灰度分布越均匀，相关性越大。③熵：描述纹理的复杂程度，羊毛纤维图像熵值更大，因其纹理相对杂乱。④方差和：表明了图像纹理的周期性，相比羊毛而言，羊绒纤维纹理周期性更强，其方差和更大。

2.2.3 边缘特征

HOG特征描述子[15]对梯度和方向比较敏感，图像边缘特征主要由梯度大小和方向决定，因此HOG可以很好的描述图像轮廓。基本原理：将图像划分成多个小单元格(cell)，相邻2×2个cell的梯度方向直方图作为这个小块的特征，然后进行归一化抑制噪声的影响，合并整幅图像所有区块的特征作为该图像的HOG特征。梯度的幅值和方向为：

(6)

(7)

式中：Gx(x,y)、Gy(x,y)分别为像素点x方向和y方向上的梯度。计算式见式(8)(9)：

Gx(x,y)=H(x+1,y)-H(x-1,y)

(8)

Gy(x,y)=H(x,y+1)-H(x,y-1)

(9)

式中：H(x,y)为点(x,y)处的像素值。

羊绒和羊毛纤维的边缘轮廓不同，羊绒鳞片结构多呈环状，而羊毛呈瓦状结构。纤维骨架图像的边缘轮廓特征比原始羊绒羊毛纤维SEM图像清晰，基于骨架图像提取HOG特征能够很好地描绘图像的形状信息。图3分别展示了羊绒和羊毛纤维骨架图像提取HOG特征的可视化图像。

图3 纤维骨架图像HOG特征

3 实验结果与分析

试样由榆林科技局提供，依据GB/T 14593—2008《山羊绒、绵羊毛及其混合纤维定量分析方法 扫描电镜法》中的制样方法，采集羊绒羊毛纤维图像各400张。拍摄仪器为Quanta 450FEG扫描电子显微镜(美国FEI公司)，放大倍数为1 000倍，图像大小为256像素×256像素。

羊绒羊毛纤维识别实质上是一个二分类问题，可通过计算准确率At来衡量识别效果。其定义为：

(10)

(11)

(12)

式中：Ac、Aw分别为羊绒、羊毛的识别率，%；Rc、Rw分别为正确识别羊绒、羊毛的图片数量；Tc、Tw分别为羊绒、羊毛样本图片的数量。实验过程中训练集和测试集比例设置为7∶3，SVM核函数选择径向基核函数。

3.1 特征维数选取

HOG特征维数与图像大小和cell大小的关系为：

(13)

式中：M、N分别为图像长和宽，像素；n为单元格像素大小。本文选用16像素×16像素大小的cell，由上式计算可得256像素×256像素大小的纤维图像HOG特征维数为2 304维。高维数据表述性更强但同时也存在大量的冗余信息，直接与纤维几何和纹理特征串联融合不仅会给分类速度带来极大的负担，且存在高维特征淹没低维特征的风险，因此需要对纤维轮廓特征进行降维。

本文利用主成分分析(principal component analysis，PCA)对HOG特征向量进行降维。通过设置不同维数大小的参数，经实验分析比较选择最佳维度。考虑到特征维数越高，纤维分类需要消耗的时间越长，因此选择在满足较高识别率的情况下所用时间最短的特征维数。表1为HOG特征降维维度与识别率、消耗时间的关系，可知最佳维度为30维，当特征维度为80维时，分类识别率更高，但花费的时间代价却大大提高。最终选择维度为30维HOG特征向量进行融合。

本文实验环境为：Intel(R) Core i7-8750H 2.20 GHz，内存为8 GB，软件为matlab R2018b。

3.2 滤波结果分析

图4为羊绒和羊毛纤维获取鳞片骨架时匹配滤波和传统方法对比图，这里传统方法采用文献[8]中方法，经边缘检测、图像增强后进行阈值分割。图4(a)为羊绒与羊毛纤维去除背景后的SEM图像，图4(b)是经图像增强，边缘检测、二值化传统方法处理后的纤维骨架图像，图4(c)为匹配滤波后的纤维骨架图像。对比图4(b)(c)可以看出，匹配滤波在获取羊绒羊毛纤维鳞片骨架中表现良好，抗干扰能力强，而传统方法易受到噪声、亮度的影响。纤维SEM图像在拍摄过程中，不可避免会受到拍摄条件、光照不匀等的影响，匹配滤波鲁棒性更强。本文取σ为2，经试验，L=9、T=100时滤波效果最好。

图4 匹配滤波和传统方法对比图

为了比较匹配滤波前后对纤维图像分类性能的影响，分别提取滤波前后羊绒和羊毛纤维GLCM、HOG特征向量，送入SVM分类器进行分类。测试结果如表2所示，可以看出滤波后纤维分类正确率有所提升，表明匹配滤波后的纤维骨架图像纹理信息更清晰，特征表述更准确。

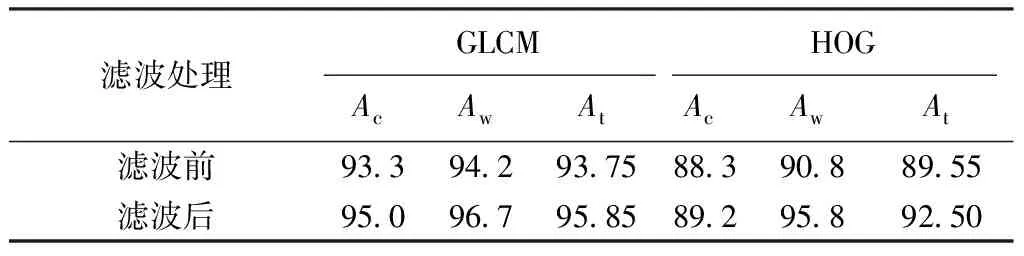
表2 滤波前后分类正确率比较 %

3.3 不同方法比较

目前，基于图像处理与计算机视觉的羊绒羊毛纤维识别方法有很多。如文献[9]利用SURF特征算子进行纤维分类识别，通过构建码本将图像映射为关于视觉单词的直方图，最后采用SVM分类，在小样本情况下有较高的识别率。文献[10]使用LBP将图像转变为二进制编码，送入SVM进行分类，通过实验表明了该方法的可行性。文献[11]从每幅图像的GLCM中提取了5个二次统计量，使用SVM作为分类器，取得了不错的效果。图5为本文方法与文献[9-11]不同特征方法识别率对比图，比较可知本文使用方法能够达到更高的识别率，此外，识别效率也优于文献[9]。

图5 不同特征提取方法识别率对比图

4 结束语

本文提出一种基于匹配滤波和多特征融合的方法，对羊绒羊毛纤维电子显微镜图像进行分类来达到纤维识别的目的。该方法对采集的原始纤维图像去除背景后经匹配滤波法分割纤维骨架，针对纤维骨架图像的几何特征、纹理特征和边缘特征，提取其灰度直方图统计特征、GLCM特征及HOG特征，多特征融合特征共同描述纤维图像信息，最后借助SVM分类器进行分类训练。实验结果表明，相比于其他鉴别方法，本文使用方法准确度更高，且在确保识别率的情况下兼顾识别速率。此外，该方法还可应用于兔毛、牦牛绒等其他动物纤维的检测。