Data-SSI与图论聚类结合识别果树固有频率

许林云，韩元顺，陈 青，姜 东，金 晶

Data-SSI与图论聚类结合识别果树固有频率

许林云，韩元顺，陈 青，姜 东，金 晶

（南京林业大学机械电子工程学院，南京 210037）

果树的固有频率是林果振动采收机械设计的重要依据之一。为有效识别果树的固有频率，该研究提出了基于数据驱动随机子空间Data-SSI（Data-driven Stochastic Subspace Identification）法与图论聚类稳定图相结合、仅以果树的输出响应信号对果树进行固有频率识别的方法，以尽量减少人为主观因素的影响。将该方法用于一棵室内小型银杏树和一棵室外较大银杏树固有频率的识别并与冲击力锤频谱测试结果进行对比分析。结果表明，室内小型果树在随机激励下采用本文方法识别结果与频谱试验结果最大相对误差为4.17%；室外大型果树在环境激励下所提方法识别结果与频谱试验结果平均相对误差为2.88%，最大相对误差为6.02%。本文方法对仅基于输出响应信号的果树固有频率识别具有一定可行性，可为果树智能化共振采收时快速准确确定共振频率提供参考。

振动；收获；固有频率；Data-SSI法；图论聚类

0 引 言

机械振动采收是林果机械化收获作业的有效手段之一[1]，根据激振位置的不同主要分为树干式、树枝式与树冠式。树干式或树枝式振动采收机械利用一定形式的激振设备对树干或树枝施加振动激励，强迫果树振动，使果实产生惯性力，当果实惯性力大于果实的果柄结合力，果实脱落[2]。国内外学者针对振动参数对振动采收的影响、果树的模态和振动响应等方面进行了大量的研究。研究表明当振动采收设备激励频率接近整个树或某分枝的固有频率时会产生共振现象，使得果枝产生更强烈的振动位移或加速度，若能充分利用共振作用，则能够以较小的激振力产生较为理想的采摘效果[3]，达到降低能耗，缩小机型等目的。

果树的固有频率为林果振动采收机械设计的重要参数之一，不同果树的固有频率受品种、树龄和生长态势等因素影响各有差别，获取果树固有频率较为常见的方法有模态试验分析法[4]、理论建模分析法[5]、有限元法[6]，其中以模态试验法最为直接。多数学者对果树进行模态试验时采用人工激励的方式，通过获取果树系统输入与输出信号，计算其频率响应函数或传递函数获得系统的固有频率。Du等[7]采用激振器在室内对甜樱桃树进行了2～40 Hz正弦激励，可获取该频率范围内果树所有的共振频率，但试验工作量较大。Lin等[8]采用锤击法对室内“Y”型银杏树进行了频谱测试，通过人工施加激励方式能够较准确地获取激励力与响应之间的关系，但是该种激励方式适用于小型果树。在对大型果树进行激励时很难引起有效的冲击响应。Damien等[9]采用绳拉法对海松进行了自由振荡试验，有效获取了树木的基频与阻尼比，但局限于基频的获取。

此外，多点激励与单点响应以及多点激励与多点响应的方法也被经常用于一些大型结构模态试验当中，如王桂伦等[10]采用单点拾振的方法对悬挂的铰接式空间桁架结构进行了模态试验分析，获得了其固有频率与振型。顾培英等[11]采用双向多输入多输出法对渡槽排架结构进行了模态试验研究，模态识别精度较好，但试验工作量及操作便捷性要稍差于单向单输入多输出的方式。

总体而言，现有获取果树固有频率的模态试验法存在以下问题：1）户外试验时振动台、激振器等试验设备携带与安装不便；2）采用力锤对较大的果树进行激励时，测试信号信噪比不高，且易对果树树皮造成损伤；3）采用多点激励的试验方式工作量大且操作不便；4）利用频响函数或传递函数需要获取输入激励信号，频谱曲线峰值的拾取具有一定的人为主观性。

基于此，本文将大型工程结构环境激励下模态识别的时域方法——数据驱动随机子空间（Data-driven Stochastic Subspace Identification, Data-SSI）法，应用于具有复杂生长结构的果树上进行固有频率识别，尤其针对田间果树，可以利用自然风激振的方法，能够在不损伤果树结构的情况下有效识别出果树的固有频率，以减少输入激励信号的环节，降低测试工作量，准确判别果树的固有频率，并为智能化共振采收提供思路与方法。

1 Data-SSI及模态频率自动拾取方法

1.1 Data-SSI

数据驱动随机子空间法(Data-SSI)具有抗噪能力良好、适用于密集模态识别的特点，在基于环境激励的模态参数识别领域取得了良好的应用效果[12]。Data-SSI法以状态空间方程为基础，仅基于系统输出完成模态参数的识别[13]。Data-SSI法主要应用于机械工程设备的模态参数识别，虽然果树结构具有复杂性和差异性，且树体材质具有各向异性，但果树由激振引起的响应均可认为处于微振动响应状态，因此可将果树振动系统作为线性振动系统，具有与复杂工程机械振动与响应相似的特征。因此，本文尝试将Data-SSI应用到果树固有频率识别之中。

果树可视其为一个多自由度系统，其运动方程可用二阶线性微分方程描述：

对式（1）进行变量替换、模态缩减、离散化处理后获得如式（2）所示的离散随机状态空间模型：

其中y为输出向量；为系统的状态向量；x+1为系统在+1时刻的状态向量；为状态空间矩阵，反映系统本身的构成信息；为输出矩阵；w和v分别为过程噪声和测量噪声。

Data-SSI法主要通过求解状态空间矩阵的特征值来获得系统的模态参数。主要计算流程为：

1）通过加速度传感器测得果树测点的加速度响应数据，直接将响应数据组成Hankel矩阵，将Hankel矩阵（）划分成过去输出行空间Y和将来输出行空间Y：

其中Y、Y是Hankel矩阵分块行；0|2i-1下标第一个数字表示Hankel矩阵左上角元素的时间系数，第二个数字表示左下角元素的时间系数。

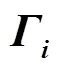
3）对投影矩阵O进行奇异值分解（Singular Value Decomposition, SVD）可得：

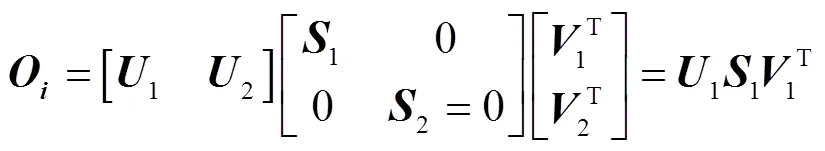
其中1为对角线元素全大于零的对角矩阵；2为零矩阵；1、2、1、2均为正交矩阵。

比较式（4）和式（5）可得：

其中ξ为阻尼比；ω为圆频率，rad/s；Δ为采样时间间隔，s；a和b为特征值的实部和虚部。

根据式（9）可求得系统的固有频率：

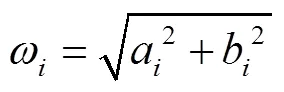
1.2 系统定阶与模态自动拾取

在随机子空间法模态识别过程中估计系统阶次是关键环节，较为常见的方法为奇异值分解法与稳定图法[14]。式（7）中奇异值矩阵1的对角元素包含了系统的阶次信息，当系统不含噪声时可将奇异值不为0的数目设为系统定阶，但噪声干扰使1的维数大幅增加，此时用奇异值来定阶会存在较大误差。传统稳定图确定系统阶次min到max进行迭代计算，一般取最小阶次min=2，迭代次数大、计算时间长，还需人为参与真实模态与虚假模态的辨识，难以实现自动化辨识，且对经验性要求较高，具有一定的人为主观性[15]。

本文参考奇异值分解计算结果设定系统的最小阶次min与最大阶次max进行迭代计算，以减少计算时间，再采用图论聚类算法对稳定图中数据进行聚类，实现模态参数的自动识别，有助于降低人为因素的影响。

图论聚类法的前提需要将待聚类的数据表示为一个带权的无向图。在图论中，2点间无箭头的连线称为无向边e，由点和无向边构成的图即为无向图，记为=(,)，其中，分别为无向图的点集合与边集合。图的边对应最小数据间的相似性度量，给图中每条边e赋以权值(e)，那么可生成满足下列条件的最小生成树MST（Minimum Spanning Tree）：

式中E为赋以权值的边的集合，为E中的元素，为边的数量，=1,2,…。

图论聚类算法步骤如下：

1）利用prim法在图上构造最小生成树；

4）每棵树视为一个聚类，完成分割。

阈值定义对聚类结果具有至关重要的作用。本文主要研究果树系统的固有频率，故可针对两固有频率点之间的距离d来定义阈值进行聚类，本文根据Magalhães等[16]定义的模态距离公式，综合考虑频率与阶次2个指标定义2个频率点之间的距离为

其中f、f分别表示Data-SSI算法计算所得的第与第个模态的频率，W、W分别表示频率和阶次在计算频率距离中的权重。考虑频率贡献率要远大于阶次，聚类后稳定图应形成纵向稳定轴的形式，本文设置W、W分别为0.9和0.1。

采用核密度函数统计分析稳定图中各频率点的距离分布情况，这些点在核密度函数曲线上形成多个波峰与波谷，选取核密度函数的第一个峰值点作为距离d的阈值，对最小生成树进行分割，完成聚类。

1.3 响应信号去噪处理方法

动态系统在环境激励下的响应通常具有小振幅和高噪声[17]，因此利用传感器采集到的结构加速度响应信号也存在趋势项与毛刺等噪声[15]。需要对所采集的信号进行去直流、去趋势和去毛刺等去噪处理后才能输入到识别系统中，以提升算法的精度。本文采用去趋势波动分析法和Savitzky-Golay滤波法对原始信号进行降噪处理[18]。

2 基于Data-SSI的果树固有频率识别流程

基于Data-SSI识别果树固有频率的技术流程如图1所示，主要包括自然环境激励下果树响应信号采集、响应信号预处理、Data-SSI模型识别和聚类稳定图辨识真实固有频率4部分。

具体步骤如下：

1）采集环境激励下果树响应信号；

2）采用DFA法和Savitzky-Golay滤波法对原始信号进行降噪处理；

3）采用奇异值假定系统的阶次，取最小阶次min，由于特征值一般以共轭复数形式出现，以2个步长为单位增至max；

4）基于数据驱动的随机子空间法识别果树的固有频率，并作出稳定图；

5）基于图论聚类法，针对稳定图进行聚类，当聚类完成后，统计每个聚类中包含的固有频率个数，并将聚类结果中聚类数目少于N的结果剔除，提取离聚类中心最近的数据为识别结果，完成果树固有频率自动识别。

3 算法验证

理论上，对果树采用锤击法可将果树的全部固有频率激发出来。实际上，对于田间大型果树，因锤击法均为人工手持力锤冲击果树，不仅冲击能量有限，且冲击力只能沿某一方向，致使许多固有频率无法有效激发出来。因此，本文对室内小型果树采用激振器产生随机振动响应信号，同时尝试利用自然风激振田间大型果树形成振动响应信号，分别应用Data-SSI算法果树各自的固有频率，并通过传统的试验频谱曲线进行验证。

3.1 室内试验

3.1.1 试验材料与方法

本文以银杏树为对象，于2020年8月7日在南京林业大学校内采伐一棵适用于室内试验的小型银杏树进行相关试验测试及算法识别，验证仅基于系统响应信号进行固有频率识别结果的精确性。室内试验在树木采伐后的3 d内完成。采伐后的银杏树用地钳固定在地面上，如图2，因银杏树树形属于合轴分枝结构，由2个主要分枝构成，一般果树同一个枝或干上具有较一致的频谱特性[10]，因此在树干及2个分枝上各布置1个测点，树干测点1距夹持点0.6 m，2个侧枝测点2和3分别距分叉点0.8 m，测点1、2、3处树干和树枝直径依次为36.83、18.14和17.18 mm。

以银杏树主干生长方向为向建立空间直角坐标系。采用功率放大器（DH5874）推动激振器（DH40500）在树干距测点1下方0.1 m处沿向施加随机激励，将三向加速度传感器（1A313E）固定于各测点处，传感器坐标方向与试验坐标方向一致，应用多通道动态信号测试分析系统（DH5922D）和DHDAS动态信号采集分析软件同时采集各测点向的随机响应信号，采样频率为2 kHz，每次采样时间为15 min，共采集3次。

为了对比各测点基于Data-SSI的固有频率识别结果，在采集工作完成后，采用冲击力锤进行频谱测试，使用力锤（LC-02A）在激振位置处平行于向施加脉冲激励，同时记录力锤输入脉冲信号与各测点响应信号，利用Matlab软件按式（11）计算各测点的频率响应函数，通过频谱曲线峰值获取各测点的固有频率。

式中()为果树的频响函数；()为加速度信号的傅里叶变换；()为力锤脉冲信号的傅里叶变换。

林果机械振动采收作业所采用的频率区间主要为15～25 Hz[8]，因此本文对果树固有频率所关注范围设定为0～30 Hz。

3.1.2 结果与分析

Data-SSI法可直接利用传感器所获取的响应数据进行参数识别，将测点响应数据组成列Hankel矩阵，理论上→∞，但实际上不可能无穷大，采用的是有限时间点的数据，且计算数据过大会导致计算效率降低，本文参考王志远、王燕等[19-20]研究，选取各测点采样时间中75 s响应信号，共计9×106个数据。首先对各测点的响应信号进行一定的降噪处理，将处理后的信号构造成为3 000×3 000的Hankel矩阵，对Hankel矩阵进行奇异值分解，3个测点的奇异值分解结果如图3所示，由于各测点响应信号的不同，3个测点的奇异值分解结果也各不相同，噪声干扰导致难以依据非0元素数目判断系统的阶次，但3个测点的奇异值曲线在某一峰值后，曲线波动有所减缓，未再出现明显大峰值，可假定此峰值对应的阶次为模型计算的最小阶次min，则3个测点的最小阶次分别32、36和28。何杰[21]认为最大模型阶次设定为真实阶次的2倍能满足准确性与计算效率，Ubertini F等[22]认为选择min≈max/2较为合适。因此本文设定max≈2min，设定3个测点的最大阶次依次为64、72和56。

基于Data-SSI算法识别出的测点固有频率绘制如图4所示3个测点的原始稳定图。可以看出，原始稳定图中真实固有频率会反复出现，但还存在大量的虚假固有频率，如图4a中在1、9.5 Hz等频率附近聚集了大量真实固有频率点，在1～9.5 Hz范围内离散分布众多虚假固有频率点。真实固有频率点会反复出现，较为集中，可形成近似轴线的形式，而虚假固有频率则较为分散，不能形成近似轴线的形式。人为拾取真实固有频率存在一定的主观性，当原始稳定图中的稳定点较为密集，或某些虚假的固有频率点聚集在某频率附近时，则会干扰人工选取结果，如图4c中1～2.5 Hz范围内存在大量的稳定点，同时一些稳定点集中在29 Hz频率的轴线附近，难以确定其是真实的或虚假的，对人为拾取结果造成较大困扰。因虚假固有频率一般较为离散，不同阶次下有着较大差别，本文采用基于距离的图论聚类法对真实固有频率进行聚类再拾取，以提高固有频率识别的效率。

以图4为基础，采用prim法依据式（10）计算2个频率稳定点之间的距离d，得到如图5所示的最小生成树，图中每2个稳定点之间都以1条最小边相连，考虑频率贡献率要远大于阶次，尽量保证聚类后稳定图形成纵向稳定轴的形式。对式（10）计算所得距离d进行核密度函数估计，如图6，选取核密度函数曲线第一个峰值所对应的频率结果作为对最小生成树进行分割的阈值，得到3个测点的分割阈值依次为0.46、0.81和0.70。

基于各测点的距离阈值分别对相应的最小生成树进行分割，移除稳定点间距离d大于阈值的边，获得如图7所示的聚类后稳定图，经过基于距离图论聚类，形成了各种规模大小不一的类，稳定点较多的类则形成了竖向稳定轴的样式，便于固有频率的有效提取。参考汤宝平等[23]对于聚类数目阈值N的设定，本文模型计算阶次基本位于20～80阶，故设定N=5，通过剔除稳定轴中稳定点数目少于5的结果，提取离聚类中心最近的数据作为识别结果，至此完成各测点的固有频率识别，具体结构如表1。

图8为锤击法获得的测点1，2，3加速度响应信号，应用公式（11）计算得各测点的频谱曲线，通过拾取3个测点的频谱曲线峰值获得对应测点的各阶固有频率，如表1，并将Data-SSI法处理结果与锤击法试验值进行比较，计算其相对误差。受不同测点位置处果枝直径及树叶的质量等因素的影响，各测点的固有频率既有一定的相似性，也存在一定的差异性。从表中数据可以看出，室内小型果树基于Data-SSI法所识别的各阶固有频率与频谱试验结果之间具有很好的对应性，且相对误差较小，平均误差为2.14%，最大误差为4.17%，在可接受范围之内，说明基于Data-SSI法识别果树固有频率具有一定的可行性，也具有一定的精确度。

表1 室内试验Data-SSI与频谱测试结果

3.2 室外试验

为了验证Data-SSI法对室外田间果树固有频率的识别正确性，本文以一棵较大银杏树为对象进行固有频率识别，该银杏树位于南京林业大学校内（江苏省南京市，32.1°N，118.8°E），树龄约18 a（图9），树高约6 m。

于2020年8月29日14:00－18:00（阴天，北风4级，29 ℃）对该银杏树进行自然风试验环境下随机激励引起的加速度响应振动试验。在该银杏树主干上布置了2个测点（测点T1、T2），4个主侧枝上各布置1个测点（测点S1～S4），图9为测点布置示意图，对应各测点位置处的枝干直径及位置参数如表2。以银杏树主干生长方向为向建立空间直角坐标系。将6个三向加速度传感器（1A313E）固定于各测点处，传感器坐标方向与试验坐标方向一致，应用多通道动态信号测试分析系统（DH5922D）和DHDAS动态信号采集分析软件同时采集各测点向的随机响应信号。设定采样频率2 kHz，每次采样时长30 min，共采集3次。

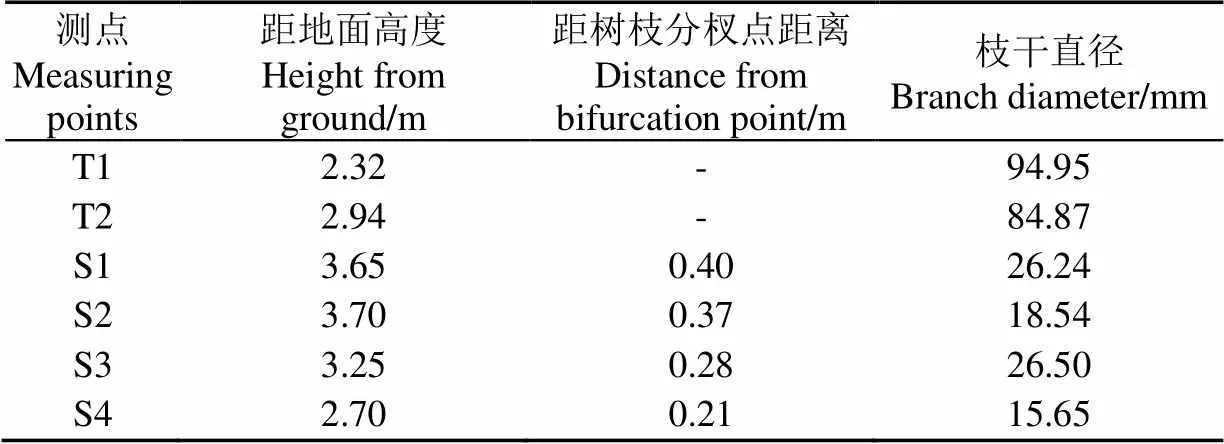
表2 测点位置及直径

图10a为树干测点T1的一段原始响应信号，信号中含有直流分量、毛刺等大量噪声。利用Matlab软件按照1.3节所述方法对原始信号进行去直流处理，去除直流分量后的响应信号较原始信号整体有所上移。如图10b，通过去趋势项与毛刺得到最终响应信号，较原始信号中尖峰与突变大量减少。

依照第2节基于Data-SSI识别果树固有频率识别技术流程对该测点去噪后的响应信号进行基于Data-SSI的固有频率识别。图11为测点T1的原始稳定图、最小生成树和聚类后的稳定图，其余测点也依照识别流程进行处理，3次采集的各测点固有频率识别均值结果如表3。

为了对比识别结果，在自然环境激励下加速度信号采集工作结束后，同样对该树使用力锤进行频谱测试。由于室外试验环境复杂、干扰较多，同时果树较为高大，力锤所施加的脉冲激励不足等问题，试验测试得到的数据信噪比较低，影响了频谱估计的准确度。图12为室外银杏树各测点实测频谱曲线，各测点频谱曲线在低频0～10 Hz内波峰很少，在10～30 Hz内存在大量波峰，但某些部位的曲线波峰较微弱，难以判断此处是否存在固有频率，对频谱估计结果造成一定的影响，因此在处理各测点Data-SSI辨识频率与实测频率对应关系时，将实测固有频率与所辨识固有频率非常接近的值作为同等阶次进行比对分析。

表3 室外试验Data-SSI法与频谱测试结果

从表3结果可以看出，T1、T2、S1与S2测点处所识别出的1阶固有频率即基频与频谱曲线所得的具有较好的对应性，但S3与S4测点在0～3 Hz上频谱曲线较平缓，难以获取峰值确定其基频，不能良好对应。除基频外，因力锤施加激励的方式存在激励不足、信噪比低的问题，同时激振力传递至各测点会发生一定的衰减，造成各测点频谱曲线存在一些微弱波峰，给人为拾取波峰造成很大的困难，对频谱估计结果造成一定影响，Data-SSI识别与峰值拾取所获得的各阶固有频率对应较好的是测点S1、S2与S3，测点T1、T2与S4的对应效果较差。

就对应的各阶固有频率看来，由于室外测试环境更加复杂，且环境激励并不时刻满足白噪声的假设，相较于辨识结果的相对误差有所增大，平均误差为2.88%，最大误差为6.02%，但总体而言绝大部分对应的固有频率相对误差均在5%之内，基于Data-SSI法的自然环境激励下果树固有频率辨识结果具有一定的精确性。在采用人工激励对果树进行频谱试验较为困难亦或试验结果不太理想时，基于Data-SSI的果树固有频率辨识不失为一种行之有效的方法。

4 讨 论

林果振动采收机械的激振频率决定振动收获的质量与效率，在强迫振动期间，果树根据施加的激励频率会做出不同的响应，本质上是由果树的冠型结构特征、木材物理性质等固有特性共同决定[24]。获取果树的固有频率有助于了解其在动态载荷下的响应，且利用共振现象设置合理的激振频率也有助于提高果实的分离率。随机子空间识别法（Stochastic Subspace Identification）是近年来最流行的识别方法之一[25]，作为一种时域辨识方法，其仅基于系统的响应数据完成参数辨识，能够克服频域识别方法中存在的一些缺陷。本文将该方法应用于果树的固有频率识别并进行了试验验证，在一定程度上证明了该方法的可行性与有效性，后续的工作中，需要更多试验与数据进一步支撑该方法的适用性，同时，SSI法也具有很大的改进空间。

1）当输入激励为白噪声时，SSI法具有高鲁棒性与效率优势，但如果激励中含有非平稳成分，其鲁棒性就会有所减弱[26]。果树田间试验中存在非平稳效应，例如输入信号（一般为自然风激励）不能时刻满足白噪声假定。若要进一步提高SSI法识别果树固有频率的鲁棒性及适用性，还需综合考虑不同果树冠型、树高、树径及其生长环境等因素，同时，在不同自然风激励下该方法识别的可行性与有效性还需进一步地试验探究。亦可借鉴一些学者针对非平稳环境激励下SSI法识别的研究，从而提高算法本身的适用性，如Benveniste等[27]验证了非平稳环境激励下SSI法识别模态参数的鲁棒性与一致性，Zhi、Chen等[26, 28]提出了一种基于平均相关信号的随机子空间方法（Average Correlation Signals based Stochastic Subspace Identification）在非平稳响应数据下对重型卡车底盘车架系统模态参数进行了有效识别，胡异丁等[13]开展了放宽环境激励的白噪声假设的延时随机子空间法研究，能够有效剔除非白噪声激励引起的虚假模态。

2）SSI法作为模态参数识别方法研究热点，其理论及应用方面正在不断发展，众多学者围绕SSI法在模型定阶、Hankel矩阵维数参数选择、剔除虚假模态等问题进行了大量的研究，如辛峻峰等[29]研究了SSI法中Hankel矩阵维数对于识别精度影响。王志远等[19]提出了基于模糊c-均值聚类的多阶随机子空间法以剔除虚假模态，通过某电网相量测量单元（Phasor Measurement Unit, PMU）实测数据验证算法的鲁棒性。在实际果树模态参数识别应用中，为使该算法更加稳定、精度更高、效率更快，还需进一步的研究与探索

5 结 论

为解决传统人工激励的模态试验法在果树系统固有频率识别时存在的一些问题，本文引入Data-SSI和图论聚类稳定图相结合的方法对果树系统仅基于输出响应信号进行固有频率的识别，对室内小型银杏树和室外较大银杏树在本文所提方法的固有频率识别结果与频谱试验结果进行了对比分析：

1）基于Data-SSI法并结合基于距离阈值的图论聚类稳定图法，在识别结果提取过程中减少了人为因素的影响；

2）可有效用于室内小型果树在激振器产生的随机激励下的固有频率识别，Data-SSI法与冲击力锤频谱试验所得结果平均相对误差为2.14%，最大误差为4.17%，计算精度较高、识别结果较为可靠；

3）基于室外较大银杏树在环境激励下所采集的加速度响应数据，运用所提方法进行固有频率识别，发现Data-SSI法与冲击力锤频谱试验相对应的结果平均相对误差为2.88%，最大相对误差为6.02%，较室内误差有所增大，但大多数识别结果误差小于5%，证明所提方法在基于环境激励下的较大果树的固有频率识别中的具有一定的可行性。所提方法在室外环境下难以对果树进行激励或激励效果不太理想时具有一定的应用价值。

[1] 散鋆龙，杨会民，王学农，等. 振动收获过程中杏果实脱落的动态响应[J]. 农业工程学报，2018，34(18)：68-75.

San Yunlong, Yang Huimin, Wang Xuenong, et al. Dynamic response analysis of apricot fruit dropping during vibration harvesting[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(18): 68-75. (in Chinese with English abstract)

[2] Sessiz A, Özcan M T. Olive removal with pneumatic branch shaker and abscission chemical[J]. Journal of Food Engineering, 2005, 76(2): 148-153.

[3] Tinoco H A, Ocampo D A, Pe A F M, et al. Finite element modal analysis of the fruit-peduncle of Coffea arabica L. var. Colombia estimating its geometrical and mechanical properties[J]. Computers & Electronics in Agriculture, 2014, 108: 17-27.

[4] Castro-Garcia S, Castillo-Ruiz F J, Jimenez-Jimenez F, et al. Suitability of spanish ‘Manzanilla’ table olive orchards for trunk shaker harvesting[J]. Biosystems Engineering, 2015, 129: 388-395.

[5] Crooke J R , Rand R H . Vibratory fruit harvesting: A linear theory of fruit-stem dynamics[J]. Journal of Agricultural Engineering Research, 1970, 14(3):195-209.

[6] Bentaher H, Haddar M, Fakhfakh T, et al. Finite elements modeling of olive tree mechanical harvesting using different shakers[J]. Trees-Structure and Function, 2013, 27(6): 1537-1545.

[7] Du X, Chen D, Zhang Q, et al. Dynamic responses of sweet cherry trees under vibratory excitations[J]. Biosystems Engineering, 2012, 111(3): 305-314.

[8] Lin H, Xu LY, Zhou HP, et al. Relationship between frequency spectrum characteristics and vibration responses of Ginkgo biloba trees during mechanical harvesting operation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(17): 51-57.

林欢，许林云，周宏平，等. 机械采收作业中银杏树频谱特性与振动响应关系研究[J]. 农业工程学报，2017，33(17)：51-57. (in English with Chinese abstract)

[9] Damien S, Thierry F. A mechanical analysis of the relationship between free oscillations of Pinus pinaster Ait. saplings and their aerial architecture[J]. Journal of Experimental Botany, 2005, 56(416): 1563-1573.

[10] 王桂伦，姜东，周李真辉，等. 铰接式空间桁架结构模态试验研究[J]. 振动与冲击，2019，38(12)：252-257.

Wang Guilun, Jiang Dong, Zhou Lizhenhui, et al. Modal experiment for a spherical hinged space truss structure[J]. Journal of Vibration and Shock, 2019, 38(12): 252-257. (in Chinese with English abstract)

[11] 顾培英，邓昌，王岚岚，等. 渡槽排架结构人工激励模态试验分析[J]. 振动与冲击，2019，38(7)：146-154.

Gu Peiying, Deng Chang, Wang Lanlan, et al. Modal test analysis for an aqueduct bent structure under artificial excitation[J]. Journal of Vibration and Shock, 2019, 38(7): 146-154. (in Chinese with English abstract)

[12] Fan G, Li J, Hao H. Improved automated operational modal identification of structures based on clustering[J]. Structural Control and Health Monitoring, 2019, 26(4): e2450.

[13] 胡异丁，李丹，任伟新，等. 基于延时随机子空间方法的非白噪声环境激励结构模态参数识别[J]. 振动与冲击，2015，34(8)：71-76.

Hu Yiding, Li Dan, Ren Weixin, et al. Modal parameter identification of structures under non-white noise ambient excitations using delay index based stochastic subspace identification method[J]. Journal of Vibration and Shock, 2015, 34(8): 71-76. (in Chinese with English abstract)

[14] 程永欢，陈彦江，李勇，等. 基于环境激励的连续刚构桥模态参数识别及有限元模型修正[J]. 工业建筑，2014，44(S1)：331-336.

Cheng Yonghuan, Chen Yanjiang, Li Yong, et al. Operation model identification and FE model updating of continuous rigid frame bridge based on environmental excitation[J]. Industrial Construction, 2014, 44(S1): 331-336. (in Chinese with English abstract)

[15] 陈永高，钟振宇. 环境激励下桥梁结构模态参数识别的改进随机子空间算法[J]. 振动与冲击，2020，39(16)：196-204.

Chen Yonggao, Zhong Zhenyu. An improved stochastic subspace method for modal parameter identification for bridge structures under ambient excitation[J]. Journal of Vibration and Shock, 2020, 39(16): 196-204. (in Chinese with English abstract)

[16] Magalhães F, Cunha Á, Caetano E. Online automatic identification of the modal parameters of a long span arch bridge[J]. Mechanical Systems & Signal Processing, 2009, 23(2): 316-329.

[17] Li Z, Fu J, Liang Q, et al. Modal identification of civil structures via covariance-driven stochastic subspace method[J]. Mathematical Bioences and Engineering, 2019, 16(5): 5709-5728.

[18] 任刚，贾继德，梅检民，等. 基于变分模态分解和去趋势波动分析的柴油机振动信号去噪方法[J]. 内燃机工程，2019，40(2)：76-81.

Ren Gang, Jia Jide, Mei Jianmin, et al. Vibration signal denoising method of diesel engine based on VMD and DFA[J]. Chinese Internal Combustion Engine Engineering, 2019, 40(2): 76-81. (in Chinese with English abstract)

[19] 王志远，龙呈，常晓青，等. 基于FCM聚类的随机子空间低频振荡模态识别算法[J]. 电力系统及其自动化学报，2020，32(4)：69-75.

Wang Zhiyuan, Long Cheng, Chang Xiaoqing, et al. Recognition algorithm for Low-frequency oscillation mode through stochastic subspace based on FCM clustering[J]. Proceedings of the CSU-EPSA, 2020, 32(4): 69-75. (in Chinese with English abstract)

[20] 王燕，杭晓晨，姜东，等. 协方差驱动随机子空间的Toeplitz矩阵行数选择方法[J]. 振动与冲击，2015，34(7)：71-75.

Wang Yan, Hang Xiaochen, Jiang Dong, et al. The selection method of toeplitz matrix row number based on covariance driven stochastic subspace identification[J]. Journal of Vibration and Shock, 2015, 34(7): 71-75. (in Chinese with English abstract)

[21] 何杰. 基于随机子空间算法的桥梁结构模态参数自动化识别[D]. 成都: 西南交通大学，2016.

He Jie. Atomatic Identification of Bridge Structure Model Parameters Based on the Stochastic Subspace Identification[D]. Chengdu: Southwest Jiaotong University, 2016. (in Chinese with English abstract)

[22] Ubertini F, Gentile C, Materazzi A L. Automated modal identification in operational conditions and its application to bridges[J]. Engineering Structures, 2013, 46: 264-278.

[23] 汤宝平，章国稳，陈卓. 基于谱系聚类的随机子空间模态参数自动识别[J]. 振动与冲击，2012，31(10)：92-96.

Tang Baoping, Zhang Guowen, Chen Zhuo. Automatic stochastic subspace identification of modal parameters based on the hierarchical clustering method[J]. Journal of Vibration and Shock, 2012, 31(10): 92-96. (in Chinese with English abstract)

[24] Sola-Guirado R R, Jimenez-Jimenez F, Blanco-Roldan G L, et al. Vibration parameters assessment to develop a continuous lateral canopy shaker for mechanical harvesting of traditional olive trees[J]. Spanish Journal of Agricultural Research, 2016, 14(2): 79-89.

[25] Liu F, Zhang H, He X, et al. Correlation signal subset-based stochastic subspace identification for an online identification of railway vehicle suspension systems[J]. Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 2020, 58(4/6): 569-589.

[26] Zhi C, Wang T, Gu F, et al. The average correlation signal based stochastic subspace identification for the online modal analysis of a dump truck frame[J]. Journal of Vibroengineering, 2015, 17(4): 1971-1988.

[27] Benveniste A, Fellow, IEEE, et al. Nonstationary consistency of subspace method[J]. IEEE Transactions on Automatic Control, 2005, 52(6): 974-984.

[28] Chen Z, Wang T, Gu F, et al. Characterizing the dynamic response of a chassis frame in a heavy-duty dump vehicle based on an improved stochastic system identification[J]. Shock and Vibration, 2015, 2015: 1-15.

[29] 辛峻峰，盛进路，张永波. 数据驱动随机子空间法矩阵维数选择与噪声问题研究[J]. 振动与冲击，2013，32(16)：152-157.

Xin Junfeng, Sheng Jinlu, Zhang Yongbo. Study on relation between noise and matrix dimension of data-driven stochastic subspace identification methtod[J]. Journal of Vibration and Shock, 2013, 32(16): 152-157. (in Chinese with English abstract)

Natural frequency identification of fruit trees by combination of data-driven stochastic subspace identification and graph theory clustering method

Xu Linyun, Han Yuanshun, Chen Qing, Jiang Dong, Jin Jing

(,210037,)

Mechanical vibration harvesting is one of the most effective means in the mechanized harvesting of fruit. Two types are mainly divided in the vibration harvesting machinery, including the shaking and comb brush type. In shaking machinery, the vibration excitation equipment is used to excite the trunk or branch, thereby forcing the fruit tree in response to the vibration, and finally the fruit moves in a certain form to produce the inertial force. As such, the fruit falls off, particularly when the inertial force of fruit is greater than the binding force of the fruit stalk. Nevertheless, the vibration transmission of branches varies in the different types of fruit trees, or the different shapes of crown structure in the same kind of fruit trees. In essence, the internal structure and inherent characteristics of fruit trees determine the dynamic characteristics. Correspondingly, the dynamic response of fruit trees depends mainly on the tree structure and inherent features. The natural frequency of fruit trees is determined by the structure and natural characteristics. The natural frequency of fruit trees is one of the most important parameters to design the vibration harvester of fruit trees. The natural frequency can commonly be obtained in the modal test. The traditional modal test is mostly artificial excitation, difficult to cause effective attenuation response for the fruit trees with complex structure, and the accuracy of frequency identification is limited by the accuracy of frequency spectrum test. In this study, a combination was proposed to integrate the data-driven stochastic subspace identification (SSI) and graph theory clustering stability diagram, in order to effectively identify the natural frequency of fruit trees. The data-driven SSI showed excellent noise immunity suitable for dense modal identification. Only the output response signal of fruit trees was used to identify the natural frequency of fruit trees. The actual response signal of the fruit tree structure was directly collected for parameter identification. The link of the input excitation signal was reduced significantly, particularly on the technical requirements and workload. In the process of noise reduction, an order determination of the system was processed, including the data-driven SSI, stabilization diagram generation, graph theory clustering, and the response signal of fruit trees under random or environmental excitation. As such, the natural frequency of fruit trees was effectively identified to minimize the human subjective factors. A field test was performed on a small indoor ginkgo tree and a large outdoor ginkgo tree. The natural frequency was also compared with the impact hammer frequency spectrum. The results showed that there was an excellent correspondence between the natural frequencies identified by data-driven SSI and the impact hammer frequency spectrum, where the relative error was small, the average error was 2.14%, and the maximum error was 4.17%. Furthermore, the average relative error between the recognition of outdoor large fruit trees under environmental excitation and the corresponding frequency spectrum was 2.88%, and the maximum relative error was 6.02%. In general, the relative errors were less than 5% in the most corresponding natural frequencies. Consequently, the data-driven SSI and graph theory clustering were feasible for the natural frequency identification of fruit trees using the output response signals. The stable graph with the distance threshold was utilized to reduce the influence of human factors, while improving the efficiency of natural frequency identification. The finding can provide a promising application in mechanical vibration harvesting, particularly where it is difficult to apply artificial force to fruit trees, or the effect of artificial force is not ideal in an outdoor environment.

vibration; harvesting; natural frequency; data-driven stochastic subspace identification method; graph theory clustering

许林云，韩元顺，陈青，等. Data-SSI与图论聚类结合识别果树固有频率[J]. 农业工程学报，2021，37(15)：136-145.doi：10.11975/j.issn.1002-6819.2021.15.017 http://www.tcsae.org

Xu Linyun, Han Yuanshun, Chen Qing, et al. Natural frequency identification of fruit trees by combination of data-driven stochastic subspace identification and graph theory clustering method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(15): 136-145. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.15.017 http://www.tcsae.org

2021-04-28

2021-06-16

国家重点研发计划（2016YFD0701501）

许林云，博士，教授，博士生导师，研究方向为林果振动收获机械。Email：lyxu@njfu.com.cn

10.11975/j.issn.1002-6819.2021.15.017

S225.93

A

1002-6819(2021)-15-0136-10