基于Geogebra的中职数学可视化教学实践

袁兰兰

摘 要：本文以Geogebra软件在中职数学中发挥的可视化功能为切入口，从数学问题可视化、数学猜想可视化以及数学概念可视化三个方面进行实践研究，将中职数学中比较抽象、空间度较强的知识点以一种动态的过程演变、可视化的形式进行最终呈现，使学生理解知识的原理，真正掌握知识点，更好地进行知识正迁移。

关键词：Geogebra    可视化    中职数学

Geogebra自2006年正式发布后，在数学教育界得到越来越多的认可。Geogebra支持几何、代数、统计、微积分等教学，几乎覆盖整个数学教学领域。借助该软件，教师可以设计更直观的教学方式，为学生创造更直观的学习环境。

一、数学问题可视化

数学探究的源头是问题，教师利用Geogebra的动态演示功能为学生创设易于认识问题的良性认知环境，将数学问题以动态的方式呈现在学生面前，使数学问题更具直观性和形象性，便于激发学生的学习兴趣，从而高效地提出问题和解决问题。

（一）轨迹追踪，理解数学问题

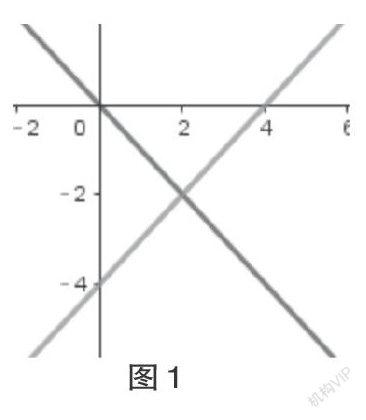
案例1.集合的交

问题：设集合A={（x，y）|x+y=0}，┤集合B={（x，y）|x-y=4}，┤求A∩B。

集合的交是中职数学第一章第三节的内容，主要引导学生掌握三类集合的交集求法，其中点集的交是一个难点，学生普遍不理解问题中的点集具体是什么，更无从求解点集的交。运用Geogebra中的轨迹追踪功能，就能形象地展示出集合A、B中的所有点（见图1），学生通过观察得出求点集的交只需求方程组的解。

（二）视图变换，掌握数量关系

案例2.球的表面积与体积

问题：把一个半径为R的球放入棱长为4的正方体中，测得球底距正方体底面为3，求球的半径R。

球是中职数学第九章第五节的内容，由于学生空间想象能力普遍较弱，不能较好理解题意，所以教师可以运用Geogebra中的三视图功能，从不同角度向学生展示题干中的数量关系。首先，以直观图的方式引导学生直观理解问题;变换角度，从上方俯视，学生进一步理解球与正方体的截面是圆且是球的小圆;从前方正视，学生清晰地看到一个直角三角形（见图2），从而引导学生轻松解决问题。

二、数学猜想可视化

猜想是数学探究教学过程中的一个重要环节，可以提升学生的想象力和创造力。教师对学生的猜想不能轻易地加以肯定与否定，要用科学的态度来对待学生的猜想与发现。教师可以运用Geogebra對学生的部分猜想进行验证，从而提高学生参与课堂互动的积极性，扩大学生的知识面，促进数学创造力的形成。

案例3.球的体积公式

（一）静态展示，直接猜测结论

师：观察三个等底等高的圆柱、半球、圆锥的体积关系。

师：写出圆柱和圆锥的体积公式。

师：根据三个等底等高的圆柱、半球、圆锥的体积关系，猜想半球的体积公式。

（二）动态截图，直观验证猜想

在Geogebra的3D绘图区绘制等底等高的圆柱、圆锥以及半径与圆柱高相等的球。

师：我们用一个平面去截球和圆柱中挖去圆锥（同底等高）这两个几何体（见图3），截面分别为什么图形？

生4：圆、圆环。

师：拖动截面，在运动的过程中，观察截面（圆与圆环）的面积关系。

生5：在运动过程中，圆与圆环的面积始终相等，因此，上述半球体积等于柱体体积减去锥体的体积。

三、数学概念可视化

数学概念是数学知识的基础，是学生学好数学命题、数学原理、解决数学问题的关键所在。通过可视化的教学方式，教师可以帮助学生将隐性的数学知识显性化，将抽象的数学概念形象化，便于学生从系统的角度把握数学概念之间的联系。

（一）改变平面位置，体验概念相互关系

案例4.椭圆的定义

平面内到两定点距离之和为常数（大于两定点间距离）的点的轨迹为椭圆。在古希腊时期，人们通过用平面去截立体圆锥得到椭圆，拖动滑杆改变平面位置，还可以得到双曲线和抛物线，运用Geogebra可展示这一过程（见图4），因此椭圆、双曲线以及抛物线统称为圆锥曲线。教师利用Geogebra将古希腊人认知圆锥曲线的过程可视化，展示三种曲线的起源，学生理解了为何三种曲线被统称为圆锥曲线。

（二）转变视图方向，理解数学概念本质

案例5.二面角的平面角定义

以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫作二面角的平面角。

空间想象能力较弱的学生理解二面角的平面角定义是有一定困难的。教师借助Geogebra的动态展示，引导学生理解定义的三个关键点：第一，公共棱上任取一点;第二，过点分别在两个半平面内作公共棱的射线;第三，两射线所成角。通过改变点A的位置，学生观察发现角度始终不变，明白点A的选取不影响二面角的平面角的值，真正理解“任取”的缘由（见图5）;改变视角，教师引导学生直观感受平面角;固定平面BPQ，让平面CPQ绕着公共棱PQ旋转，观察得出平面角的范围为。

课堂实践证明，将Geogebra应用到中职数学课堂教学，利用Geogebra辅助讲解，学生更容易认识数学问题、检验数学猜想、掌握数学概念以及理解推理过程，学习兴趣也得到激发。

参考文献：

[1]崔丽萍.数学可视化教学及其若干范例[D].上海：上海师范大学，2006.

[2]晓霞.初中数学概念类知识的可视化研究[D].南京：南京师范大学，2014.

[3]范文贵.基于信息技术开展数学探究可视化的研究[J].中国电化教育，2008（259）.

（作者单位：嘉兴技师学院）