基于多传感器反馈的软体夹持器位置反馈方法
2021-11-25陈晓波汤健华江励赖根
陈晓波,汤健华,江励,赖根
(五邑大学 智能制造学部,广东 江门 529020)
0 引言
随着人力资源成本的不断提高,制造业开始使用机械代替人工,并开始尝试将其运用于助老助残、医疗康复、家政服务等领域。在上述非结构化、作业环境复杂多变的情况下,太过依赖结构化环境工业机器人,其作业效率、准确性、稳定性等都较难保证。因此,研究者开始将目光投向软体机器人,其从制作材料驱动源、作业方式等方面都与传统的刚性机器人具有明显的差别。相较传统刚性机器人刚度较高的机械结构、精确的位置控制精度、高速的力传递等特点,软体机器人高柔顺性、高适应性、高安全性使其在非结构化作业环境下具有比刚性机器人更好的优势。
软体夹持器凭借其高柔顺性可以对不同形状、大小的目标进行抓取,同时对抓取对象的损害极小。因此,在交互性较高的场合,软体夹持器将具有刚性夹持器无可比拟的优势,然而过分追求夹持器的柔性,虽然能够提高夹持器的环境适应能力和运动灵活性,但是也会导致夹持器的控制精度和抓取力的下降。如何解决软体夹持器的控制精度问题,使其具有较高精度的控制性能成为制约软体夹持器发展的关键性问题之一。
软体夹持器主要由软体驱动器所组成,目前常见的软体驱动器按驱动方式可简单分为以下几种:绳拉驱动器[1-3]、气动驱动器[4-5]、智能材料驱动器[6-7]、化学反应驱动器[8]、生物混合驱动器[9]、磁场驱动器[10]等。其中,由于气动驱动器以气体作为驱动源,气体以其绿色环保、易获取、质量轻等特点使得该驱动方式被广泛运用。诸如方醒[11]研制的通体由硅胶浇注而成的通用气动软体机械手,王华等[12]设计了一种由气压驱动的可实现弯曲运动的纤维增强软体驱动器,哈佛大学B.Mosadegh等[13]提出的能够在不到50 ms的时间内完成弯曲的“快速气动网格”设计等。在软体驱动器弯曲特性研究方面,黄海明等[14]将经过粗糙化的光导纤维嵌入软体驱动器内部,光导纤维由于驱动器弯曲变形会产生不同程度的光线溢出,通过测量光能损耗量就可以推断当前情况下驱动器的弯曲程度;冯乃诗等[15]通过有限元分析的方法,采用Neo Hookean模型建立了软体驱动器变形的数学模型,并建立了弯曲模型和扭转模型;张晗[16]通过分析单个驱动器力学特性,提出了基于人工神经网络的驱动器力学特性映射关系模型。
综上所述,针对驱动器可观测量不足的问题,本文设计了一款以气体驱动的具有高度的柔顺性、精确的位置控制的软体夹持器,其主要适用于对安全性、柔性要求较高的场合。首先,在驱动器结构设计优化基础上,结合多个传感器提高了驱动器可观测反馈量的冗余度;其次,通过建立驱动器在气压驱动下气压与驱动器弯曲曲率之间的映射关系,在常曲率变形的假设前提下搭建驱动器的准静力学模型,并借由仿真的方式验证模型的有效性。最后,通过位置反馈实验,验证了软体驱动器位置反馈方法的有效性和准确性。
1 软体夹持器结构设计
本文借鉴哈佛大学B.Mosadegh等[17]提出的“快速气动网格”设计,同时兼顾连接可靠、可重复拆卸、可测量软体驱动器气室等效弧长度、具有位置反馈等结构及功能特性要求。该软体驱动器主要包括网格气室基体、进气道、进气管接口、滑动轴承、线绳、嵌入其中的不可延展的柔性材料限制层、薄膜片式弯曲传感器、压觉传感器、滑动轴承固定部件。
气动软体驱动器作为典型的欠驱动驱动器,其自由度有无穷多个,而典型的控制信号为气压信号,因此仅靠气压数据估计驱动器的变形十分困难。但是使用视觉伺服的方法具有较大的局限性,主要体现在:一方面在抓取过程中,镜头的视野很难覆盖驱动器的工作范围;另一方面,驱动器容易被周围环境及被抓物体遮挡。
除了视觉伺服以外,有研究者在软体驱动器上嵌入弯曲传感器,直接使用弯曲传感器获取驱动器的弯曲曲率[18]。观测信息数量由仅有的气压数据,增加为弯曲传感器常量积分与气压,可观测数据数量增加为2,如图1所示。因此,本文采用如图2所示的薄膜式单向弯曲传感器嵌入软体驱动器内部,用于测量驱动器弯曲变形程度并反馈给控制端。
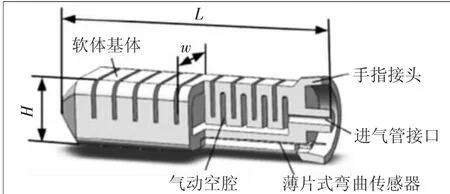
图1 使用弯曲传感器的软体驱动器示意图[18]

图2 弯曲传感器实物图
但是,即使增加了弯曲传感器,一根驱动器中可以观测的数据量也只有2个,因此,本研究主要集中在通过结构设计,增加软体手指的观测量。如图3所示,本论文研究具有位置反馈的软体夹持器,在原有气动网格模型基础上,加入了线-编码器模块。通过分析软体驱动器的变形特性及几何结构,由线-编码器模块测量得到软体驱动器弯曲变形等效弧的长度变化,从而间接获得驱动器的弯曲曲率信息。其中,为了进一步降低编码器的对于长度变化的测量误差,在软体驱动器末端固定一个滑动轴承,如图3中红圈中所示,用于放大线绳的长度变化,从而降低系统误差对于测量结果的影响,最后经过结构设计后的软体驱动器整体结构如图4所示。总体而言,通过驱动器的结构设计并结合多传感器的反馈,从而有效地增加了软体驱动器可观测量的冗余度,对于实现软体夹持器的更高精度位置控制具有重要作用。

图3 加入线-编码器模块后驱弯器弯曲变形图

图4 具有位置反馈的软体驱动器实物图
基于既有位置反馈软体驱动器的设计,制作了图5所示的软体夹持器。该软体夹持器由3 个线-编码器模块、1个亚克力材质的组装盘、3个可调节角度的驱动器夹具部件、3 个软体驱动器所组成。

图5 软体夹持器三维模型及实物图
2 准静力学模型
2.1 常曲率假设
气动网格软体驱动器是一种由多个相同且相通的网格气室组合而成,整体由硅胶材料浇注而成。软体驱动器在充入气体后能够发生弯曲形变归根结底是由于软体驱动器气室内外大气压不同。图6(a)所示为充气前驱动器气室状态,在气室未冲入气体时其内部气压同大气压一致,假设此时的气压大小为P1。在驱动器气室充入气体后,气室内部气压随着升高,气室内壁受压变形,与此同时嵌入限制层的下层,由于限制层硬度E1比硅胶硬度E2大的多,从而导致软体驱动器向嵌入有不可延展材料制成的限制层一侧发生弯曲变形,充气后软体驱动器气室状态如图6(b)所示。由分析可知:发生弯曲时驱动器顶部气室由于气室内外压力差的缘故产生膨胀,而不可延展的材料限制了软体驱动器底部的伸长,从而产生期望的驱动器弯曲变形。

图6 驱动器气室变形分析
通过借鉴连续机器人弯曲变形后的形状表示方式[19],将软体驱动器在气体驱动下弯曲形态近似看作一段常曲率圆弧。因此,软体驱动器的弯曲变形如图7所示,其中θ为软体驱动器弯曲变形之后,其每个网格气室所对应的圆心角,而总的弯曲角度为φ。由于本文设计的驱动器是单一气囊的驱动器,各个网格气室是相互连通的,因此各个网格气室在同一气压作用下变形也应该是相同的,则
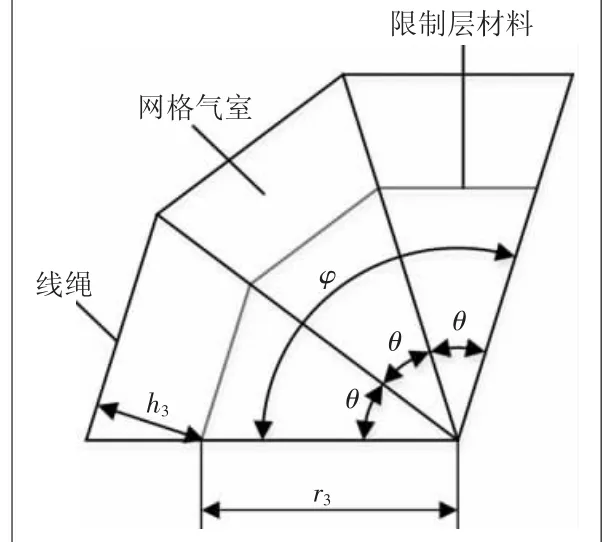
图7 软体驱动器弯曲变形角度

式中,n为软体驱动器网格气室的总数。
通过旋转编码器的标定实验可以获得驱动器弯曲变形后线绳的长度变化量l1,同时由于线-编码器模块通过滑动轴承将线绳变化量放大成2倍,因此驱动器弯曲后气室顶部的长度变化量为

式中,h3是驱动器的高度。
由于弯曲传感器嵌入到软体驱动器距离底部3 mm的硅胶内部,因此通过上述公式求得的曲率半径并非软体驱动器底面弯曲变形后的曲率半径。假设驱动器弯曲变形后,弯曲传感器所在位置与驱动器底部同心,则弯曲变形后驱动器底部的曲率半径r1为

2.2 驱动器弯曲特性分析
通过向驱动器内施加不同的气压值,探讨驱动器弯曲曲率随气压变化而变化的特性,由于驱动器整体是一个对称结构,只需要计算一半的驱动器模型即可知道整体驱动器的弯曲变形情况,其有限元模型如图8所示。同时选择二阶Yeoh模型[20],其中硅胶的材料常数C10=0.11、C20=0.02[21]。在0~60 kPa 气压之间,每隔5 kPa进行一次仿真,其结果如图9所示。

图8 有限元籍所所用驱动器模型
由图9可知,驱动器弯曲曲率随气压的增大而增大,同时在工作气压区间内呈现较好的线性关系,因此驱动器弯曲曲率同气压的关系可以表示为
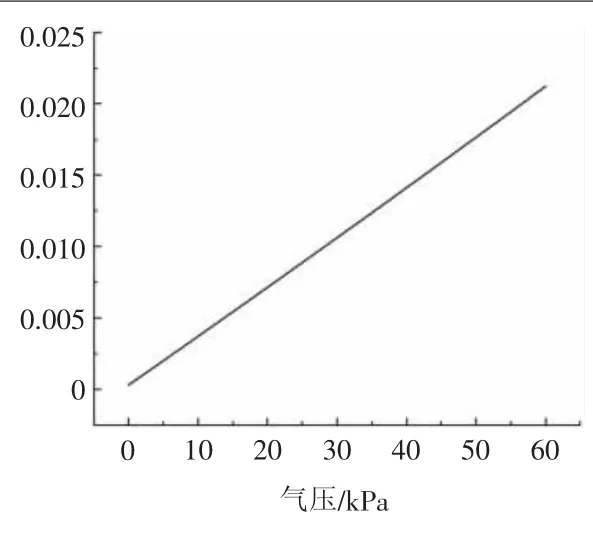
图9 有限元仿真结果
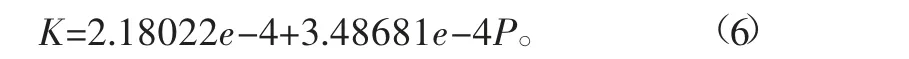
通过上述拟合线性方程即可通过代入气压值从而快速计算出驱动器在该气压条件下的弯曲曲率。
2.3 驱动器弯曲变形末
端点位置反馈模型
由于驱动器抓取物体时最先接触物体的是驱动器底部接触面,将驱动器弯曲变形后底部连接而成的圆弧看作驱动器弯曲变形曲线,驱动器弯曲变形曲线如图10所示。

图10 驱动器弯曲变形曲线示意图
在常曲率假设下,通过弯曲传感器的标定得到的表达式计算得到相应的曲率,则通过弯曲传感器预测的驱动器末端点坐标可表达为:

式中:x1是驱动器末端的横坐标;y1是驱动器末端的纵坐标;r是驱动器弯曲后底部的曲率半径,其值为曲率K的倒数。
3 软体驱动器位置反馈
3.1 传感器标定
软体夹持器作业过程中需要通过不同的传感器反馈信号获取驱动器弯曲变形后的状态,对传感器进行相应的标定可以形成较为准确的传感器反馈信号同驱动器弯曲曲率之间的映射关系。
1)弯曲传感器标定。
由于嵌入软体驱动器内部的弯曲传感器会随着驱动器弯曲变形程度的不断加深而电阻值逐渐变小。因此,假设弯曲传感器的反馈电阻值时由其平均弯曲曲率所决定的。为了验证上述这一假设,本文设计制作了如图11所示的一系列标定包,其圆弧凹槽的直接分别为35、40、45、50、55、60 mm,凹槽宽度为1.25 mm,圆弧凹槽的长度分别为20、40、60、80 mm。

图11 弯曲传感器标定板
将弯曲传感器分别嵌入标定板凹槽内并采集相应的反馈电阻值,最后对采集的数据进行整理分析,由图12可知,弯曲传感器的反馈电阻值与其弯曲曲率具有较好的线性关系,随着驱动器弯曲曲率的增大,弯曲传感器的反馈电阻随之不断增大。但是,不同弯曲长度下,弯曲传感器在同一弯曲曲率下呈现不同的反馈电阻值。因此,可以推测反馈电阻值也受到弯曲长度的影响。由于本文所使用的弯曲传感器电阻公差为±30%,对单个的弯曲传感器的标定,并不能适用于全部弯曲传感器。同时弯曲传感器一次性嵌入软体驱动器中,其使用的环境改变可能影响到反馈信号与弯曲曲率之间映射关系但却难以重新取出验证。本文通过分析软体驱动器作业时的运动特点,确定其作业时弯曲长度是固定不变的。因此,嵌入软体驱动器内部的弯曲传感器,其反馈电阻的影响因素只有弯曲曲率,能够通过提取软体驱动的弯曲曲率从而与弯曲传感器的反馈电阻形成一一对应的映射关系。
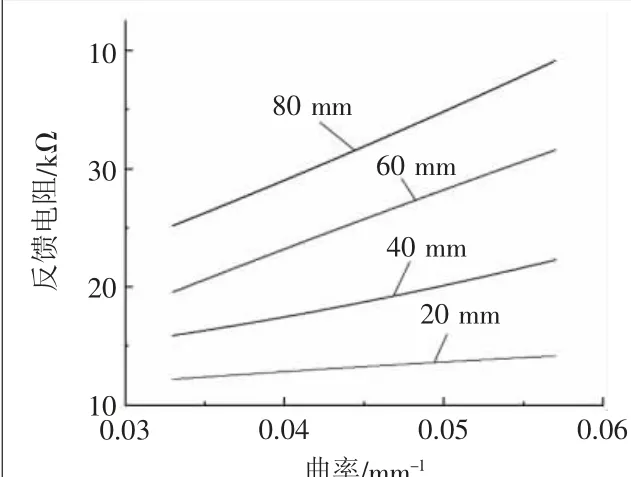
图12 弯曲传感器不同弯曲长度的反馈电阻
基于上述分析,可以将嵌入弯曲传感器的软体驱动器悬挂在图13所示的标定平台上,标定实验中采用万用表对其电阻数据进行采集,利用手动调压阀调节驱动器内气压,从而使得驱动器保持一定的弯曲状态,通过摄像头采集得到软体驱动器的弯曲图像并通过图像处理提取相应的弯曲曲率。最终,将驱动器弯曲曲率与弯曲传感器反馈电阻值绘制成图14所示散点图,并拟合获得两者映射关系式:

图13 弯曲传感器标定平台
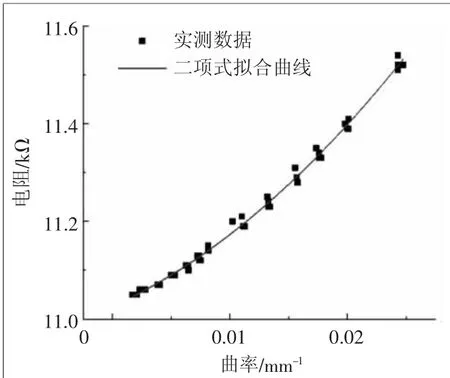
图14 弯曲曲率与反馈电阻的映射关系

2)压力变送器标定。
搭建的压力变送器标定平台,各部件连接顺序如图15所示,其主要设备包含压力变送器、可调气压阀、气泵、24 V电源、电流转电压模 块 、Arduino UNO 开 发 板、电脑、若干导线等。首先将用于采集电压信号的程序烧录进开发板内;其次,使用万用表测量电流转电压模块的电压输出信号,通过电流转电压模块上的调零旋钮将压力变送器在0 kPa 气压条件下的电压输出调零;再次,重复上一步骤,将压力变送器在60 kPa气压条件下的电压输出调整为5 V。最后,由于Arduino UNO开发板的A0引脚能够输出0~1023之间的数字,其中0对应0 V电压、1023对应5 V电压。因此,电压值与读数n1之间的关系表达式为


图15 压力变送器标定平台各部件连接顺序图
式中:u为电压值,V;n1为A0引脚读取到的读数。
由于压力变送器的微电流输出信号量程为4~20 mA,对应0~100 kPa的气压值,气压值与压力变送器反馈电流值之间的关系可表示为

式中:P为气压值,kPa;I为电流值,mA。
电流转电压模块是将4~20 mA电流信号转换成0~5 V的电压信号,其关系可表示为

综上,压力变送器标定后可以得到关于气压值与A0引脚读数之间的关系表达式为

结合弯曲传感器标定,可以将采集得到的气压值与弯曲曲率数据整理拟合,其结果如图16所示,两者之间拟合关系式可表示为
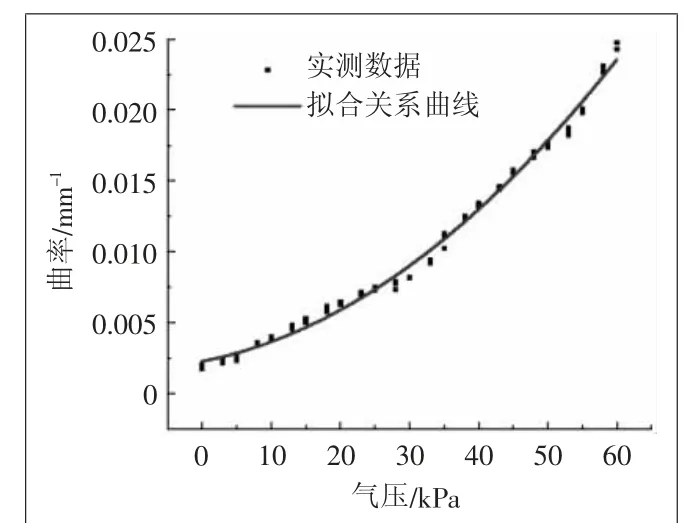
图16 驱动器气压与弯曲曲率关系

3)线-编码器模块标定。
理论上,在已知联轴器绕线位置直径的情况下,通过旋转编码器反馈的脉冲增量即可计算出线绳的变化长度。但是,由于通过小电动机绕线时线绳每一圈缠绕的长度不同,如图17所示,导致理论上的长度变化同实际长度变化存在一定的误差。因此需要将旋转编码器装配到工作环境中进行标定。

图17 联轴器绕线示意图
首先,用气泵给驱动器充入最大的工作气压60 kPa,驱动器产生弯曲变形从而使得贯穿整个驱动器的线绳长度发生变化,测量其最大的变化长度大约为80 mm。其次,搭建图18所示的编码器标定平台,编码器标定平台包括编码器、小电动机、Arduino UNO开发板、调速模块、游标卡尺、线绳、联轴器、编码器支架、导线若干等。其中,调速模块用于调节小电动机的转速,防止过快的转速将线绳拉断;小电机用于自动回收被驱动拉长的线绳,使之随机地缠绕到联轴器上绕线的位置。最后,将变化长度80 mm分为8等分,将线绳的一端系在游标卡尺上,通过游标卡尺拉动固定长度的线绳并记录对应的旋转编码器脉冲变化量n2。重复上述实验5次并将实验数据整理绘制成脉冲增量与线绳长度变化量关系曲线,其结果如图19所示。由图19可得到脉冲增量与线绳长度变化量关系表达式:

图18 编码器标定平台
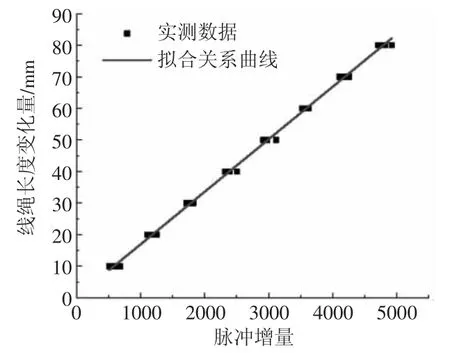
图19 脉冲增量与线绳长度变化之间的映射关系
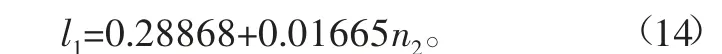
式中:l1为线绳长度变化量;n2为旋转编码器反馈的脉冲增量。
将通过图像处理提取的弯曲曲率同编码器标定前后计算的曲率作对比,其结果如图20所示。通过图20可知,标定后的旋转编码器对于曲率的反馈精度明显提高,同时在较小气压下其误差较大的原因在于小气压下线绳长度变化量小导致系统误差对计算结果造成较大影响,随着气压增大,线绳长度变化量也随之增大,系统误差对于计算结果造成的影响也随之不断降低。
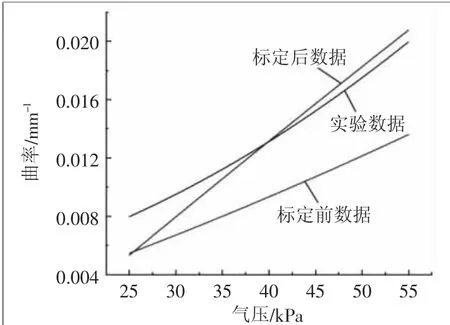
图20 线-编码器模块标定后对驱动器弯曲曲率的预测效果
3.2 驱动器末端点反馈实验
将单根的驱动器悬挂在弯曲传感器标定平台上,采用高精度调压阀体控制驱动器的输入气压。首先,实验时由于驱动器充气变形后导致贯穿驱动器网格气室上端的线绳长度发生变化,线绳又带动旋转编码器转轴转动,从而可以通过Arduino UNO开发板读取旋转编码器相应的脉冲变化量;其次,驱动器弯曲变形后其底部嵌入的弯曲传感器被动弯曲,从而导致其电阻值发生相应的变化,通过万用表测量得到相应的电阻值;最后,在驱动器正前方架设高清摄像机,采集不同气压下驱动器的弯曲变形图像,结果如图21所示。通过图像处理提取驱动器底面的弯曲曲率,然后将弯曲传感器反馈的变形弧线及旋转编码反馈的变形弧线同实验测试结果进行对比,结果如图22所示。

图21 不同气压驱动下驱动器实际弯曲效果
由图22可知,弯曲传感器反馈信号得出的驱动器弯曲弧线与实验获得的实际弯曲弧线基本重合,旋转编码器反馈信号得出的驱动器弯曲弧线与实验获得的实际弯曲弧线存在一定偏差。通过对图23(b)分析可知,其末端位置反馈的误差随着气压值的增大而减小,其原因在于随着气压增大,驱动器的弯曲变形也随之增大,不同的绕线情况对于总体线长变化影响也随之变小。
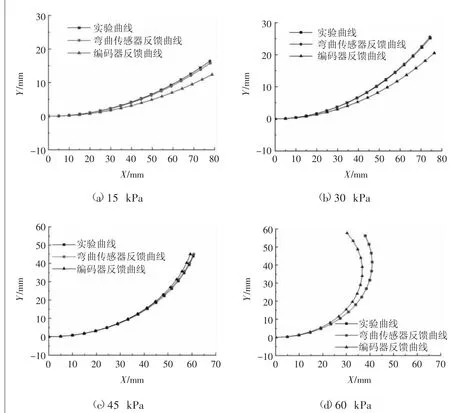
图22 实际弯曲变形曲线与反馈信号计算得出的弯曲变形曲线对比图

图23 传感器反馈末端点误差
4 结论
本文分析了软体驱动器的弯曲变形原理,并基于常曲率假设和驱动器弯曲变形后的几何特点,结合传感器反馈信号建立了驱动器弯曲曲率的数学模型,借由有限元程序仿真验证了该模型的有效性,同时指出有限元仿真没有考虑到设计参数同制作参数存在一定的误差,因此运用仿真结果拟合的映射关系对驱动器末端位置进行预测是不够准确的。继而,通过对传感器的标定获得更准确的传感器信号与弯曲曲率之间的映射关系,借由建立的驱动器弯曲曲率数学模型计算得出不同气压下驱动下驱动器末端位置,并通过实验验证其有效性和准确性。
