桩底溶洞探测中瞬时相位差强度计算方法的优化及应用*

2021-11-25石振明王登一杨沛权

工程地质学报 2021年5期

关键词：声呐端点溶洞

石振明沈健刘鎏彭铭王登一杨沛权何枭

(①同济大学地下建筑与工程系，上海 200092，中国)

(②同济大学岩土及地下工程教育部重点实验室，上海 200092，中国)

(③中国科学院武汉岩土力学研究所，岩土力学与工程国家重点实验室，武汉 430071，中国)

(④广东建科交通工程质量检测中心有限公司，广东 650506，中国)

0 引言

岩溶地貌在全球分布广泛，而我国是世界上岩溶地质发育最广泛的国家之一，总面积达344.3万平方千米(刘鎏， 2021)，约占国土面积的1/3(陈学军等， 2019)。在岩溶地貌区开展地下工程建设通常充满风险。因为时常存在无规则岩溶分布与填充情况(姚邦杰等， 2019)，不充分的桩底溶洞勘探可能导致护壁泥浆泄漏、钻孔坍塌、周围建筑开裂甚至周围建筑结构倒塌等严重工程事故(石振明等， 2016)。

传统的探测方法提供了许多桩底溶洞勘探方法，但这些方法受灌注桩桩孔内高压泥浆环境影响，无法被应用于桩底溶洞探测。而弹性波CT法(朱文仲等， 2008)和管波测试法(李学文等， 2005)虽能被用于灌注桩桩底溶洞探测，但受限于其探测精度不足以及钻孔布置繁琐，并不常被用于实际工程的桩底溶洞探测。基于这一现状，相关研究团队提出了一种钻孔灌注桩桩底溶洞声呐探测方法(刘鎏， 2021)，将桩孔中的泥浆作为声波传播和耦合的介质，利用广义S变换进行了声波信号分析，揭示了桩底声呐信号物理意义，实现了桩底溶洞的快速无损探测。但该分析方法是基于传统Fourier变换提出的，在面对桩孔内不规则多次反射面波的干扰时分析能力不足，对溶洞位置准确揭示能力受到影响。

相位是信号本质特征之一，能够表征信号任意时刻的状态，是信号分析过程中重要的考察对象。传统的信号分析方法包括相位反正切、DACM算法以及线性解调算法等。但这些方法只适用于单一分量信号，受噪声影响较大，均无法应用于桩底声呐探测的复杂信号分析。而希尔伯特-黄变换(Hilbert-Huang Transform， HHT)能够将复杂信号中的噪声滤去，从而获得信号准确的相位信息。如图1a展示了经HHT分析后得到两个不同偏移距的桩底溶洞探测信号瞬时相位信息，从图中不难发现信号相位均在-π到π间变化。图1b则展示了两信号间的瞬时相位差，可以看到瞬时相位差在2 ms及4 ms处接近于0，但这一特点仍无法直接清晰、定量地识别出来。

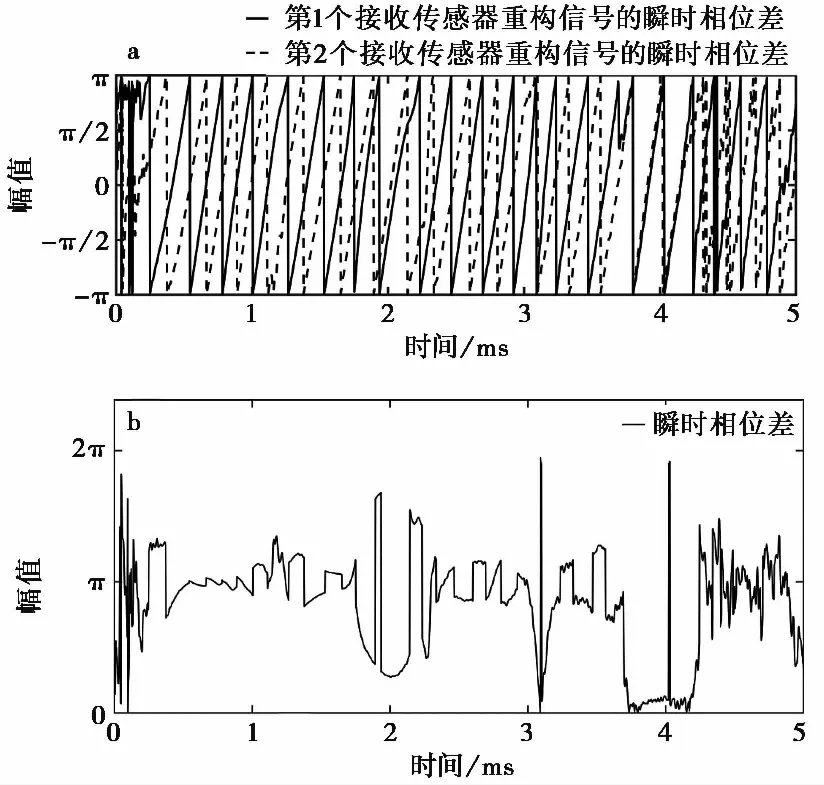
图1 瞬时相位及瞬时相位差(Liu et al.， 2021)

基于瞬时相位信息特征，学者提出了一种双通道桩底溶洞声呐探测方法(Liu et al.， 2021)。该探测方法通过在桩底布置“一发双收”(双通道即指双接收器)的声呐接发换能器，获取两道声呐应力波信号记录，运用HHT分析方法从中获得相应瞬时相位信息，并以定量指标-瞬时相位差强度(Instantaneous Phase Difference Intensity， IPDI)来衡量两道信号间的相位差异，将溶洞顶底板的有效体波反射信号从桩孔壁以及桩孔底多次反射面波信号中提取出来，从而实现溶洞顶底板的识别。

但在计算信号IPDI值时，HHT方法中各个关键参数因影响规律不清而随意选取以及IPDI图像两端可能出现的端点效应将会导致溶洞顶底板位置识别不够精准，亟待优化处理。

本文根据数值仿真模拟信号测试结果，探究了双通道桩底溶洞探测方法中IPDI分析过程的关键参数影响规律和端点效应抑制方法，提出优化建议，并结合工程现场实测信号验证了优化方法的有效性，提升了溶洞顶底板位置识别的精准度。

1 溶洞声呐探测方法及数值仿真

1.1 双通道桩底溶洞声呐探测系统

双通道桩底溶洞声呐探测系统示意图如图2所示。图中O点位于桩孔底中心处，代表了声呐应力波发射换能器。而A、B两点分别代表了两个相隔一定距离的接收换能器，接收沿桩孔壁及桩孔底传播的多次反射面波和溶洞顶底板的微弱体波反射信号。C、D点分别代表溶洞顶板和底板。图中OA、AB间距离(即发射器至接收器距离以及两接收器间距离)都是人为可调的。当根据面波波速以及接收信号主频设置AB间的距离为半面波波长时，信号记录中面波的相位差近似为±π。同时当溶洞离开桩孔底距离较远时，两接收换能器中P波反射信号的相位差就应当接近于0。反射体波相位差与多次反射面波相位差的明显不同为从信号记录中提取出所需的微弱反射体波信号并由此计算溶洞顶底板位置提供了可能。

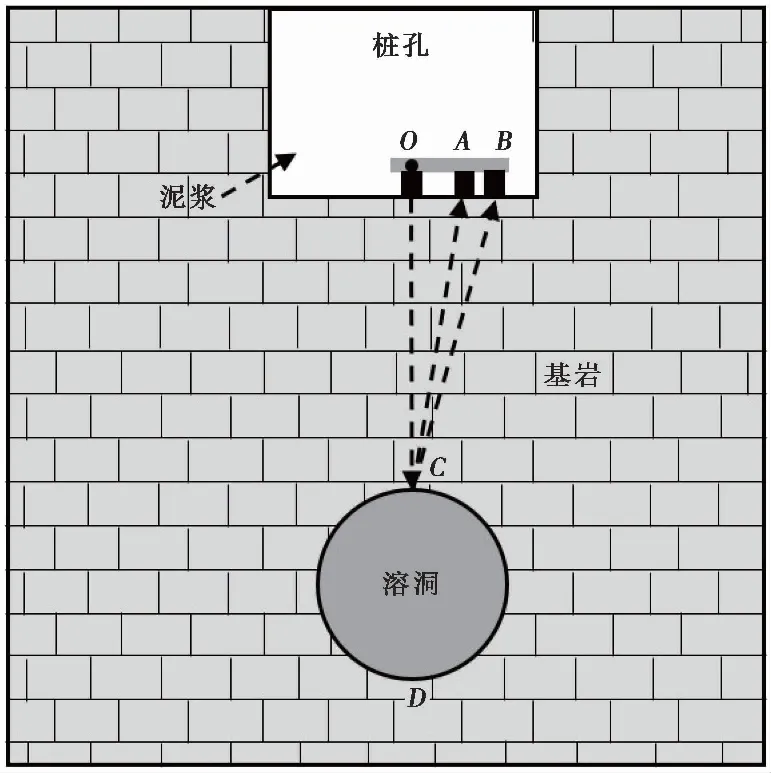
图2 双通道桩底溶洞声呐探测系统示意图

1.2 数值仿真

为进行数值模拟测试，首先建立了二维桩底溶洞声呐探测的数值模型，利用二维的黏弹性波方程(式(1)～式(3)，式中变量均以二阶张量形式表示)和交叉网格时域有限差分(Ke et al.，2016)获取数值模拟结果。

(1)

(2)

(3)

式中：vi为速度分量；τij为应力分量；ρ为介质密度；λ和G是拉梅常量；εL和εT分别为纵波阻尼系数和横波阻尼系数。

分析探测波场和波剖面包括了桩孔、基岩和桩底溶洞(图3)。模拟计算区域的大小为8m×8m，桩孔模型位于计算区域的上部中心，其直径Dp为1.6m，深度为2m。溶洞顶板距离桩孔底距离为Hc，其为直径Dc。且通过设置不同波速、密度以及阻尼系数可以模拟不同溶洞填充物情况。竖直方向的入射波将在桩底孔的中心向下发射，该点即为发射换能器，其坐标(0， 0)。同时在计算边界外加入了完美匹配边界(Perfectly matched layer， PML)(Berenger， 1994)来吸收并压制在计算边界上产生的反射以模拟波场实际传播过程。图3中PML边界厚度为2m，分布于模型四周边界。其中红色区域(见电子版文章)表示边界重合处。

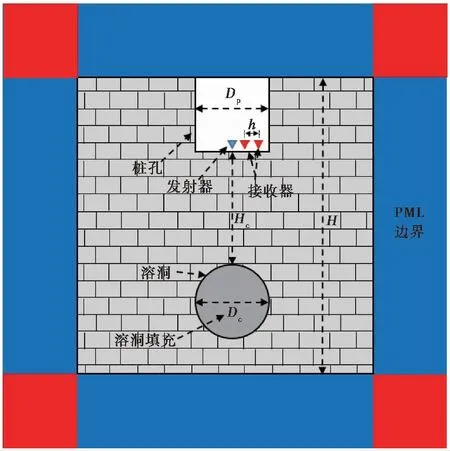
图3 桩底溶洞声呐探测数值模拟模型

数值模拟中不同介质的材料模拟参数设定见表1，其具体过程如下：

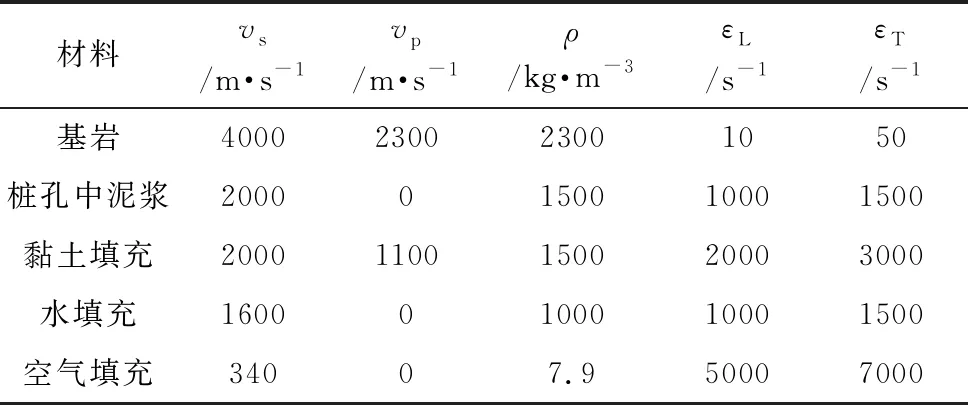
表1 数值模拟的材料参数

(1)根据桩孔和桩底溶洞的地质结构建立交叉网格时域有限差分模型，在考虑计算精度和计算成本后，选取合适空间和时间精度。此处选取空间10阶，时间2阶的差分形式。

(2)设置所有参数，包括不同材料介质物性参数以及发射、接收装置位置坐标。这里设置两接收器间距离为半面波波长。

(3)设置PML边界条件，输入PML边界参数。

(4)进行时域有限差分，求解黏弹性波动方程。

(5)记录模拟信号并使用IPDI方法对其进行分析。

1.3 IPDI计算方法

瞬时相位差强度(IPDI)其计算流程如图4所示，可以简单概括为：(1)布置探测系统，并使两个接收器之间的距离为半面波波长；(2)运用EEMD将原始信号分解为一系列固有经验模态函数(IMF)；(3)选择合适的IMF组合成为重构信号；(4)对重构信号作用希尔伯特变换得到瞬时相位，并计算瞬时相位差；(5)计算瞬时相位差强度(IPDI)，其具体定义如式(4)：

图4 瞬时相位差强度计算流程图

(4)

式中：t为任意时刻；T为信号周期，数值上等于信号主频的倒数。当t为反射波到达时刻后一个周期的中点时刻t0，I(t)达到最大值，在IPDI图像中表现为峰值。因此，反射波到达时刻ta可以定义为：

(5)

此过程中的总体平均经验模态分解(Ensemble Empirical Mode Decomposition， EEMD)过程意义在于将接受到的信号中多余噪声滤去而尽可能保留真实相位信息。其具体计算步骤如下：

(1)给待处理的信号x(t)加上一组高斯白噪声w(t)，得到新的总体信号X(t)

X1(t)=x(t)+w1(t)

(6)

(2)对X1(t)进行EMD处理，得到其分解结果

(7)

式中：c1k为分解所得的各IMF分量；r1n为分解所得残差。

(3)再给原信号x(t)添加N-1组不同的白噪声，重复EMD过程

Xi(t)=x(t)+wi(t)，i=2，3，…，N

(8)

(9)

(4)取相应的IMF均值为最终的IMF

(10)

从以上步骤可以看到，EEMD关键在于加入了N组一定幅值的白噪声来消除可能出现的模态混叠现象，而所加入白噪声的具体组数以及其相应幅值是人为决定的。这将可能影响提取出来相位信息的真实程度。关于这一方面的讨论将会在下一节详细展开。

2 溶洞探测精度影响因素分析及优化

这一部分将结合桩底溶洞声呐探测仿真信号测试采样率、EEMD中总体平均次数以及标准差对IPDI分析结果的影响规律，并尝试就这些参数取值以及端点效应的抑制给出优化意见。

2.1 采样率分析及参数优化

现实生活中我们很难记录下连续信号，因此只能通过一定的采样率将连续信号时间序列离散化(Flandrin et al.，2004)。采样率越高，越能使记录下的离散信号逼近原始的连续信号。而EEMD分解通过对信号的极值点进行插值计算来形成上下包络线，并以上下包络线的均值作为各阶IMF，因此过小的采样率可能导致信号极值点的位置和取值发生误差，最终使获得的IMF不够准确，降低了IPDI值对信号异常相位信息的提取能力(Liu et al.，2021)。

图5a展示了在采样频率分别为0.5MHz、1MHz和2MHz时计算所得的IPDI值。该算例模拟了溶洞直径为2m、溶洞顶板距桩孔底距离3m、填充物为黏土的情况。图中2 ms处和4 ms处附近的峰值分别代表了溶洞顶板以及底板的反射信号。而3 ms处的峰值代表了溶洞顶板反射PS波的垂直分量。从图中可以看到，采样率为0.5MHz和1MHz时，IPDI峰值重合，其所对应的时刻分别为：C-1.904 ms， D-3.924 ms。结合基岩波速、黏土填充波速以及式(2)可以算得溶洞顶板距桩孔距离2.928m，溶洞直径2.02m，误差均小于5%。但当采样率为2MHz时，其计算所得溶洞顶底板位置精度为未得到明显提升但运算所需时间大幅增长。

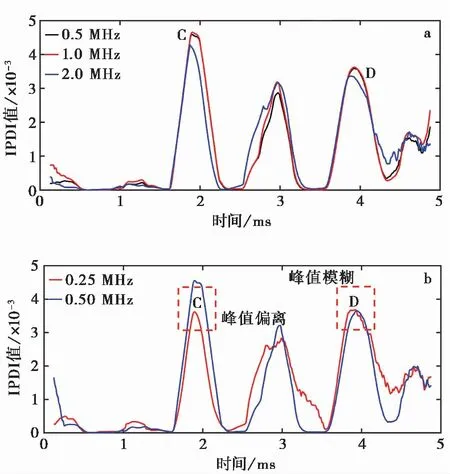
图5 信号采样率对IPDI计算结果影响

图5b展示了在采样率分别为0.25MHz和0.5MHz时计算所得的IPDI值。从图中可以发现，当采样率为0.25MHz时， 2 ms处IPDI峰值发生了偏离，其对应的时刻为1.896 ms，由此计算所得的距离偏小。并且4 ms处的峰值所对应的具体时刻辨认困难，为溶洞直径的计算制造了困难。

综合以上两例，当进行IPDI计算时，为保证计算结果的精确，采样率不宜过小，数值模拟结果表明采样率通常取0.5～1MHz能够使误差足够小。

2.2 总体平均次数以及标准差参数分析及优化

虽然EEMD是一种自适应的信号时频分析方法，但在其分解过程中仍需人为选定两个参数：总体平均次数N以及加入白噪声的标准差ε。其中：总体平均次数决定了加入白噪声的组数，而标准差则决定了白噪声幅值与原信号幅值之比。通常总体平均参数取100～200，而标准差大致取0.2能够取得比较理想的分解结果(Wu et al.，2009)。现就采样率为0.25MHz时探索这两个参数的何种取值方式能够使IPDI计算结果得到提升。

图6a展示了当标准差ε分别选取0.05、0.1、0.4时计算所得IPDI曲线。标准差为0.4及0.1时，溶洞顶板反射信号在IPDI曲线中对应的时刻均为1.896 ms；标准差为0.05时，溶洞顶板反射信号在IPDI曲线中对应的时刻为1.88 ms，其计算所得溶洞顶板距桩孔底距离(2.88 ms)误差最大。标准差为0.05及0.1时，溶洞顶板反射信号在IPDI曲线中对应的时刻均为3.896 ms；标准差为0.4时，溶洞顶板反射信号在IPDI曲线中对应的时刻为3.948ms。综合来看，当标准差取0.1时，其计算结果最准确(溶洞直径2m，溶洞顶板距桩孔底距离2.912m)。

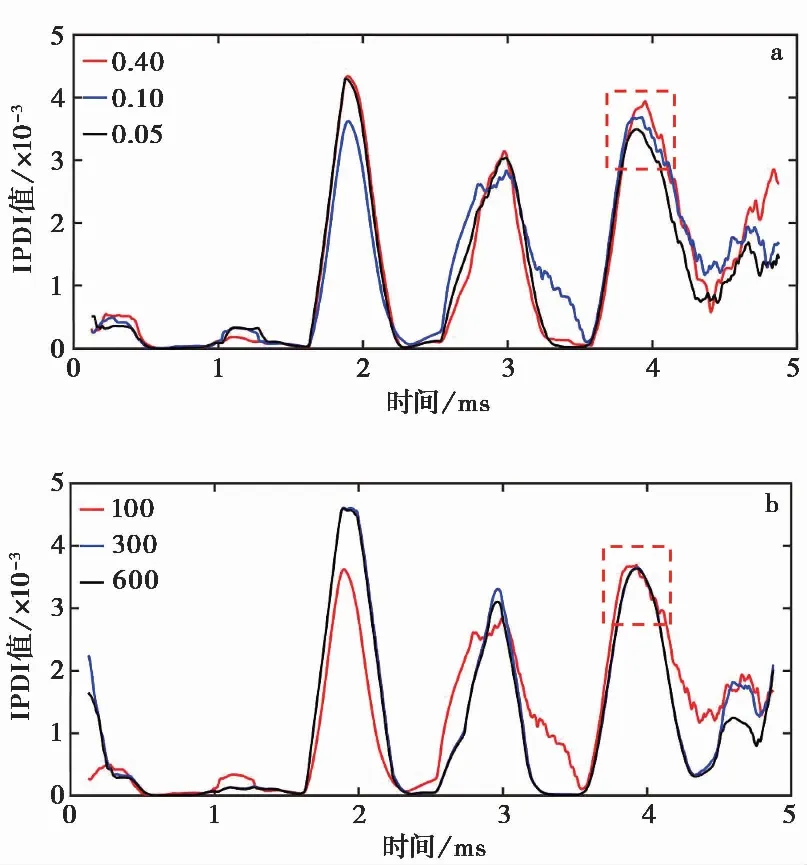
图6 EEMD参数取值对IPDI计算结果影响

图6b展示了当总体平均次数N分别选取100、300和600时计算所得IPDI曲线。溶洞顶板反射信号在IPDI曲线中对于3个总体平均次数取值均为1.896 ms；而当总体平均次数取300和600时， 4 ms处溶洞底板反射信号峰值更清晰，更容易判断其对应时刻。

综合以上分析，在进行EEMD过程中，标准差取0.1且总体平均次数取较大值如300～600能够提升最终溶洞识别准确度。这一建议与式(11)(Wu et al.，2009)相吻合。

(11)

式中：ε代表白噪声标准差；N代表总体平均次数；εn代表最终误差的标准差，即输入信号与相应IMF间的误差。

2.3 基于灰色预测模型的端点效应抑制

端点效应指溶洞声呐探测方法所计算得到IPDI图像中，其两端出现异常“飞逸”现象，如图7左右两端。端点效应作为HHT公开的七大理论问题(Rilling et al.，2009)，已经引起了学者们的广泛关注。相关理论研究表明，端点效应可能同时存在于EMD以及HT两个过程中。前者主要由左右端点插值精度差导致，后者发生的原因由傅里叶变换中“Gibbs现象”引起的频率泄露导致。

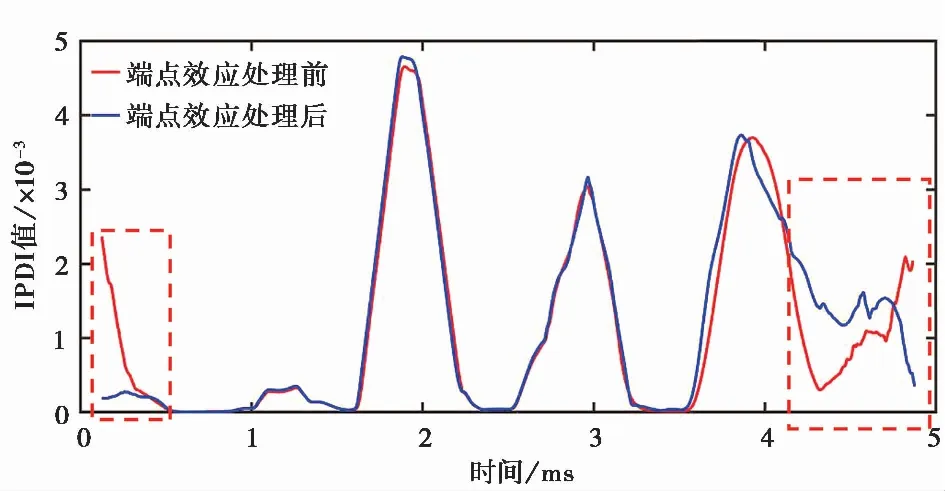
图7 端点效应抑制

为解决这一问题，本节选择了灰色模型预测模型(贺智， 2011)来进行端点效应的处理。灰色预测模型是基于灰色系统理论发展的(Kayacan et al.，2010； Li et al.，2010)，其本质在于通过运用信号端点少量数据来对信号进行延拓，包括EMD过程中根据端点极值的延拓以及HT变换前对IMF的延拓，其具体原理如下：

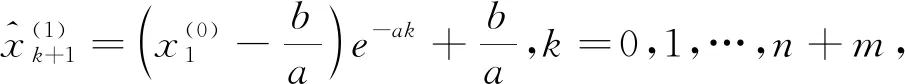
本节尝试在构造完成的重构信号基础上，在其数据两端分别拾取3m、3n个数据点，建立灰色预测模型，再各自向两端外预测m以及n个数据点，得到新的重构信号，经HT变换后再选择与原始信号相同时间段的重构信号数据点，最终计算得到IPDI值。如图7，可以看到经灰色预测模型延拓原信号数据点后，其IPDI曲线末端的“飞逸”得到明显改善，证明了此方法对改善端点效应的有效性。但同时可以发现经端点效应优化处理后其峰值位置出现了一定偏移，可能影响最终溶洞顶底板位置的判定。

3 IPDI优化方法应用

本节尝试就1个数值模拟工况以及1个现场实际工程所得信号以测试上文所述的IPDI值优化方法，并证明其有效性。下面介绍这些工况和其相应优化结果。

3.1 数值模拟工况

该工况下溶洞直径Dc设置为2m，溶洞顶板距桩孔底距离Hc设置为3m均未改变，只通过设置不同的波速、密度以及阻尼系数(表1)来模拟桩孔下部溶洞被3种不同材质的填充材料填充——水、空气以及黏土(图8)。图9a为未作优化处理的该工况下IPDI值图像， 2 ms左右处的峰值反映了溶洞顶板的反射波信号， 4 ms左右处的峰值则反映了溶洞底板的反射波信号。可以看到，只有黏土填充和水填充的IPDI图像上在4 ms处能看到明显峰值，而由于波在空气中传播速度慢导致其反射信号未在采样时窗内被捕获。为优化该工况下的IPDI值图像，采用了提高采样率至1MHz以及端点效应优化的方法(图9b)。从优化结果中可以看到，黏土填充溶洞底板反射信号IPDI峰值更明显，其对应时刻更容易判断，为3.954 ms(对应可算得溶洞直径1.938m)。而且，水填充溶洞顶板反射信号IPDI峰值对应时刻由1.898 ms变为1.961 ms，计算所得溶洞顶板距桩孔底距离的相对误差由2.8%改进为1.4%。此外，本文所采取的端点效应优化方法一定程度上压制了信号两端的“飞逸”现象。

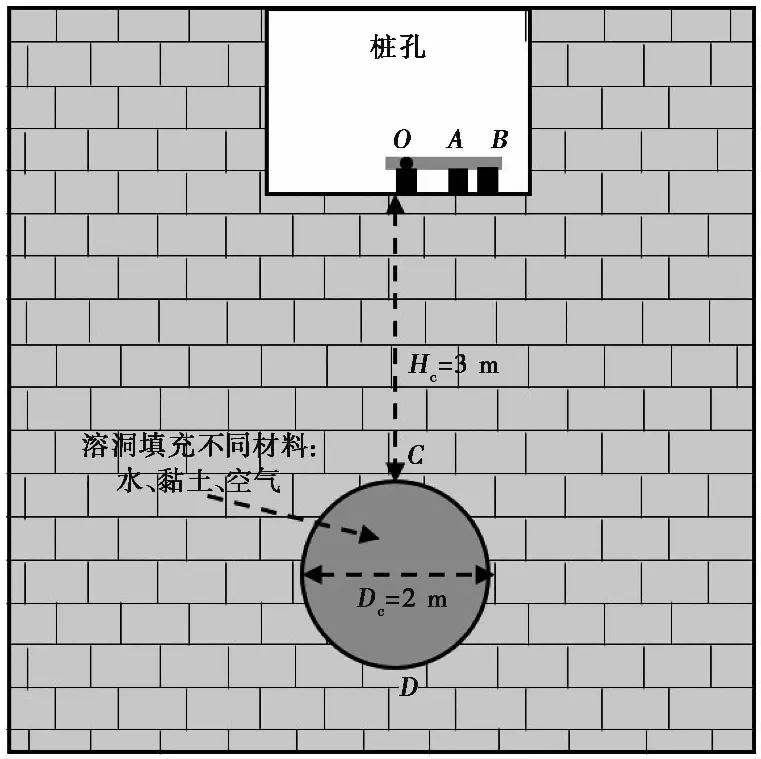
图8 数值模拟工况示意图

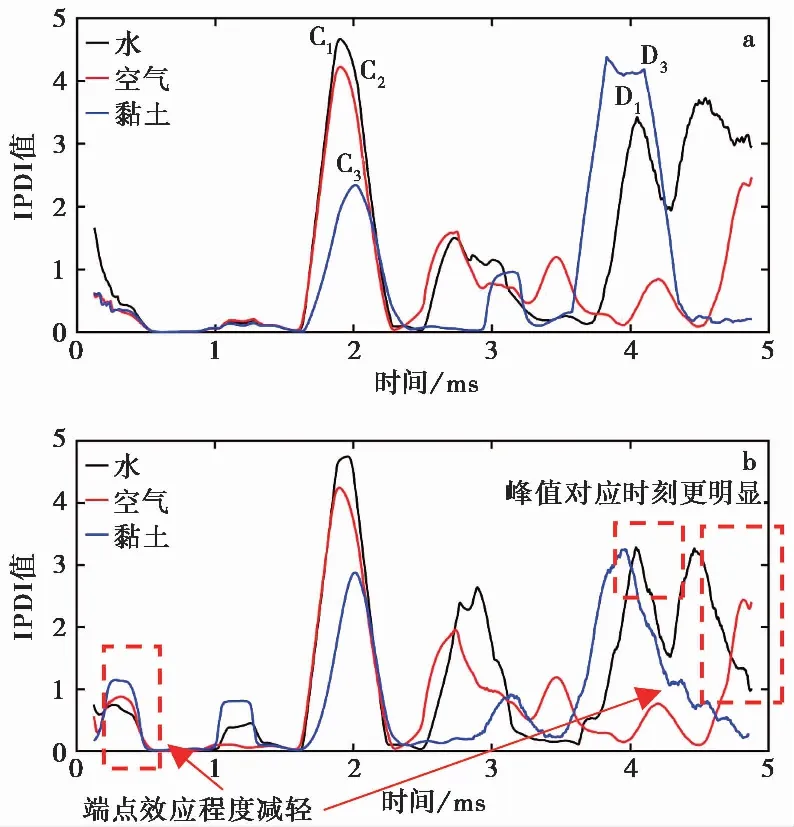
图9 数值模拟工况信号IPDI值优化结果

3.2 现场实际信号

该信号取自广清高速改扩建工程的一桩基建设场地。该工程沿线有29km的岩溶区，主要为下石炭统的浅海相夹含煤碎屑岩，由深灰、灰黑色灰岩、白云质灰岩、泥灰岩和硅质灰岩组成。旧路勘察资料、施工记录及新路初勘资料表明，岩溶区岩溶分布密度大，见洞率高，岩溶发育深度正处在路基、桥基的影响深度。为保证工程安全进行，有必要在桩基施工阶段对桩底溶洞进行详细勘察。

在桩基施工之前，该场地利用3个钻孔 Y63-1、Y64-2和 Y65-3进行了两次跨孔地震波CT成像(图10)。其反演的纵波速度剖面与钻孔柱状图基本吻合，共同表明了该场地岩溶发育且分布不均，灰岩与上覆第四纪沉积物不整合接触。仅就钻孔Y64-2，其在钻进过程中遇到串珠状溶洞，溶洞发育于32.9～34.9m、38.4～41.6m以及41.6～44.4m等多个深度处。

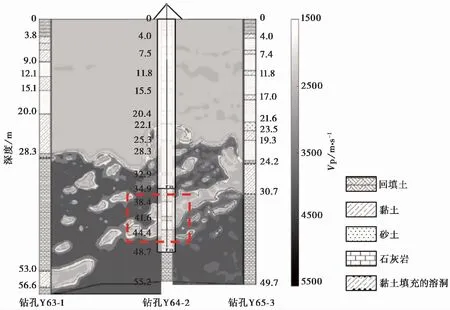
图10 跨孔地震波CT成像(Liu， 2021)

图11a为该工况下的IPDI值图像，从图中34.9m处进行的溶洞探测表示的IPDI曲线在2.42 ms处的峰值可以计算得到溶洞顶板距桩孔底3.7m，即位于38.6m深度处，这与图10中所揭示的结果相近。而48.7m所代表的曲线没有明显峰值，表明48.7m下为完整基岩。虽然34.9m处进行的溶洞探测能够揭示溶洞顶板，但其溶洞底板无法直接从探测结果曲线中读出。

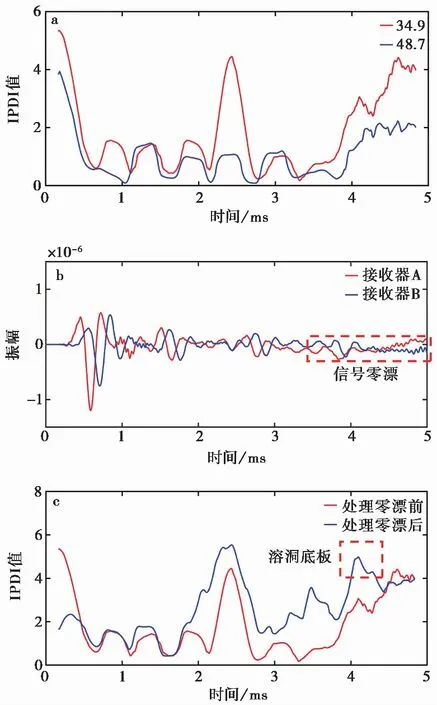
图11 实测信号IPDI优化

当我们仔细观察信号记录，不难发现在信号记录尾端发生了零漂现象，即一段时间的信号记录不再关于时间轴对称(图11b)。鉴于这一现象的存在，尝试对经过EEMD得到的重构信号进行处理，即使重构信号减去EEMD所得的最后一个残余趋势项，并再运用上文所述的灰色预测模型信号延拓方法，最终得到的结果如图11c。可以看到不仅左端端点的“飞逸”得到了抑制，而且右端原先表现为端点效应的4.09 ms处呈现了一个新的IPDI峰值。结合黏土填充的纵波波速进行计算，该峰值极可能对应图10中41.6m处的溶洞底板。

通过这一实际工程的溶洞顶底板位置探测结果优化分析，我们可以看到，当溶洞底板所对应的反射信号处于采样时窗末端时，其可能被IPDI计算过程以及采集仪器导致的零漂现象端点效应所掩盖。此时，将EEMD后得到的重构信号减去分解过程中自然得到的残余趋势项(趋势项表达了信号零漂的具体趋势)，再运用灰色预测模型进行端点效应处理，能够有效将被掩盖的溶洞底板反射信号提取出来，从而揭示出溶洞底板位置。