三峡库区典型堆积层滑坡变形滞后时间效应研究*
2021-11-25高晨曦刘艺梁易庆林陈健翔
高晨曦 刘艺梁 薛 欣 易庆林 陈健翔
(①三峡大学防灾减灾湖北省重点实验室, 宜昌 443002, 中国)
(②三峡大学三峡库区地质灾害教育部重点实验室, 宜昌 443002, 中国)
(③三峡大学湖北长江三峡滑坡国家野外科学观测研究站, 宜昌 443002, 中国)
0 引 言
我国是个深受滑坡灾害困扰的国家,每年由滑坡造成的经济损失异常惨重(许强等, 2004)。其中:堆积层滑坡是三峡水库运行过程中的重要地质灾害,其变形演化往往滞后于库水位的变化,表现出时间滞后效应,这给滑坡灾害精准预测和灾害警情准确发布造成极大困扰。堆积层滑坡变形滞后时间的研究对实现这类滑坡灾害准确预报有重要作用,同时对降低滑坡灾害造成的经济损失及人员伤亡具有重要意义(亓星等, 2020)。缪海波等(2014)以三峡库区滑坡为研究对象,通过滑体变形与滑体内部孔隙水压力变化间相关性的分析,揭示了滑体内部超孔隙水压力变化的外界因素触发机制,探讨了降雨和库水位变化作为外界因素对水压力变化的影响,该机制的揭示为解决滑坡位移预测模型考虑滞后效应提供了有益参考。杨巧佳等(2015)运用统计学方法,建立了滑坡变形滞后与库水位及降雨的回归模型,认为库水位降速对变形滞后期的影响占主导作用。石爱红等(2013)选取月降雨量与库水响应滞后影响下的库水位月平均变化量为诱发因子,采用时间序列分析方法进行分析,研究表明诱发因子对滑坡的位移变化具有重要的影响。张建等(2018)对雨水入渗规律进行分析,研究土体渗透参数与土体强度参数及迟滞现象的关联性。陈亮青等(2018)以树坪滑坡为例,研究了诱发因素对于滑坡位移变形的滞后影响。前人对研究库水位与滑坡变形滞后响应之间关系做了大量研究,对于定性分析该方面问题的述评不够全面,不能很好地阐述清楚当前研究中的不足。因此,本文在前人的基础上,以三峡库区典型堆积层滑坡——树坪滑坡为例,以实时监测数据为依据,采用集对分析法并结合层次分析法,构建滑坡加权位移向量计算模型,在滑坡加权位移演化与库水位波动相互关系定性分析的基础上,寻找滑坡加权位移与库水位下降速率相关性达到最大时的平移步数,计算出滑坡变形滞后具体时间,实现对三峡库区树坪滑坡变形滞后时间效应定量研究。研究成果可以为树坪滑坡的监测预警防治工作提供参考,对重大水利工程涉水滑坡监测预警具有一定借鉴意义。
1 基于集对分析的时间滞后模型
1.1 集对分析法基本原理
集对分析法是赵克勤于1989年提出的一种解决确定-不确定问题的新方法,能较好地实现不确定信息的整体处理(赵克勤, 2000)。刘晓等(2009)将集对分析法引入岩土变形监测分析领域,开展了滑坡变形对水库蓄水过程滞后响应的定量研究。
集对分析在一定的问题背景下,讨论的两个集合所具有的特征,进行同、异、反分析并加以定量刻画,得出这两个集合的同、异、反联系度表达式(刘晓等, 2009; 桂蕾等, 2012):
μ=a+bi+cj
(1)
式中:μ为联系度;a为同一度;b为差异度;c为对立度;i为差异度系数;j为对立度系数。
1.2 构建滑坡加权位移向量计算模型
设有Z1、Z2、Z3、…、Zm共m个监测点,第k个监测点t时刻的位移记为xt, k(t=1, 2,…,n;k=1, 2…,m),构成多点位移时序矩阵X:
(2)
考虑到每个滑坡位移监测点所处空间位置不同,在滑坡整体位移变形中所占权重大小不同,因此设监测点的权重向量W为:
(3)
则滑坡加权位移向量可表示为:
S=XWT
(4)
1.3 考虑库水位下降速率的滑坡变形滞后时间计算模型
由于三峡库区库水位的不断变化,使得库区滑坡演化受控于库水位的涨落过程。
为考察相邻监测时段滑坡加权位移演化,引入某时间段内滑坡加权位移平均变化速率阈值q(单位为mm·d-1),将滑坡加权位移变化按照“波动q1~q2内”、“大于q2”和“小于q1”,划分为“平稳增长”、“加速增长”和“减速增长”3种状态。考察库水位下降期间的波动情况,引入某时间段内库水位平均下降速率阈值p(单位为m·d-1),将相邻时段内库水位的下降速率按照“波动p1~p2内”、“大于p2”和“小于p1”,划分为“平稳下降”、“加速下降”和“减速下降”3种状态。确定阈值q和p的波动范围是进行相关性分析的关键。
通过定性分析滑坡加权位移变化与库水位下降速率相互关系,建立同异反关系判别表,如表1 所示。

表1 滑坡加权位移变化与库水位下降速率同异反关系判别
选取2012年、2013年、2014年汛雨期地表位移与库水位下降速率的监测数据,构建滑坡加权位移S={St}(t=1, 2, 3,…,n){Xt}与库水位波动L={Lt}(t=1, 2,…,n)时序,从t=2开始,可根据表1 进行n-1次判别,设其中取同、异、反的个数分别为na、nb、nc,其按式(1)联系度μ的系数为:
(5)
联系度μ刻画了某段时间滑坡加权位移和库水位下降速率的相关性,其a值越大,说明所构成的集对相关性越好。设平移步数为step,对滑坡加权位移进行等步长Δt平移,即考察t→t+1区间滑坡加权位移和库水位下降速率的相关性。取step=0, 1, 2…,搜索不同step下a的值,当a达到最大时,其对应的step与Δt的乘积即为滑坡变形滞后时间T:
T=step·Δt
(6)
2 典型滑坡分析
2.1 树坪滑坡概况
树坪滑坡地处三峡库区长江南岸,距三峡大坝约47km。树坪滑坡属于古崩滑堆积体,呈南北向展布,向北倾斜,发育于沙镇溪背斜南翼,其岩层产状为120°~173°∠9°~38°,滑坡体平均坡度为22°,属逆向坡。岩性主要为泥岩、粉砂岩夹泥灰岩。树坪滑坡总体呈圈椅状,后缘高程380~400m,前缘高程约60m,南北长约800m,东西宽约700m,面积约55×104m2,厚约30~70m,平均厚约50m,总体积约2750×104m3(卢书强等, 2014)。
2012年6月,建设了实时相对位移自动专业监测点。根据树坪滑坡多年变形特征,将其划分为主滑区和影响区,主滑区滑体上现有6个位移监测点分别为SP-2、SP-6、ZG85、ZG86、ZG87和ZG88,变形影响区有2个位移监测点为ZG89和ZG90,监测点布置如图1 所示。因监测点所处滑坡体的位置、高程和监测数据变化量等因素不同,本文选取ZG85、ZG86、ZG88和SP-2这4个监测点的滑坡变形数据作为数据来源,选取监测点的变形量如表2 所示。

表2 树坪滑坡专业监测点变形分析
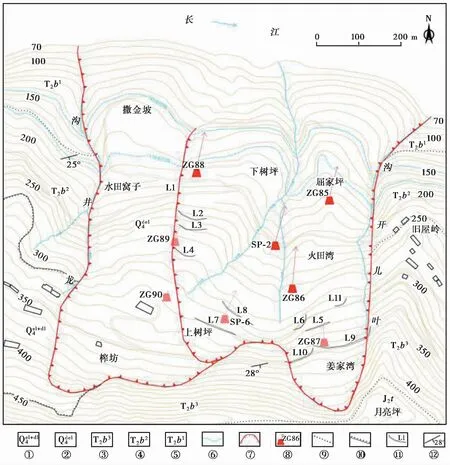
图1 树坪滑坡监测点平面布置图
2.2 库水位变化对树坪滑坡变形的影响
由于三峡库区库水位不断变化,使得库区滑坡演化受控于库水位涨落过程。从图2 可知,自三峡库区蓄水以来,当库水位下降或低水位运行期(每年4月至9月),滑坡累计位移曲线会出现一个明显的变形增长阶坎,此时各监测点位移变化幅度增大。而在库水位上升或高水位运行阶期(每年10月至次年3月),滑坡累计位移曲线相对趋于平稳,即各监测点位移变化幅度减小。因此,库水位下降与树坪滑坡变形之间具有较强的相关性。

图2 树坪滑坡地表累积位移-库水位-降雨量-时间关系
树坪滑坡地表位移变形速率与库水位升降速率间的相互关系图中(图3) 显示,从2012年到2014年,当库水位平均下降速度达到最大,而在此期间滑坡平均位移速率也达到了最大。这说明库水位下降对树坪滑坡变形影响较大,且库水位下降速率越快,造成的滑坡变形越大(肖捷夫等, 2020)。
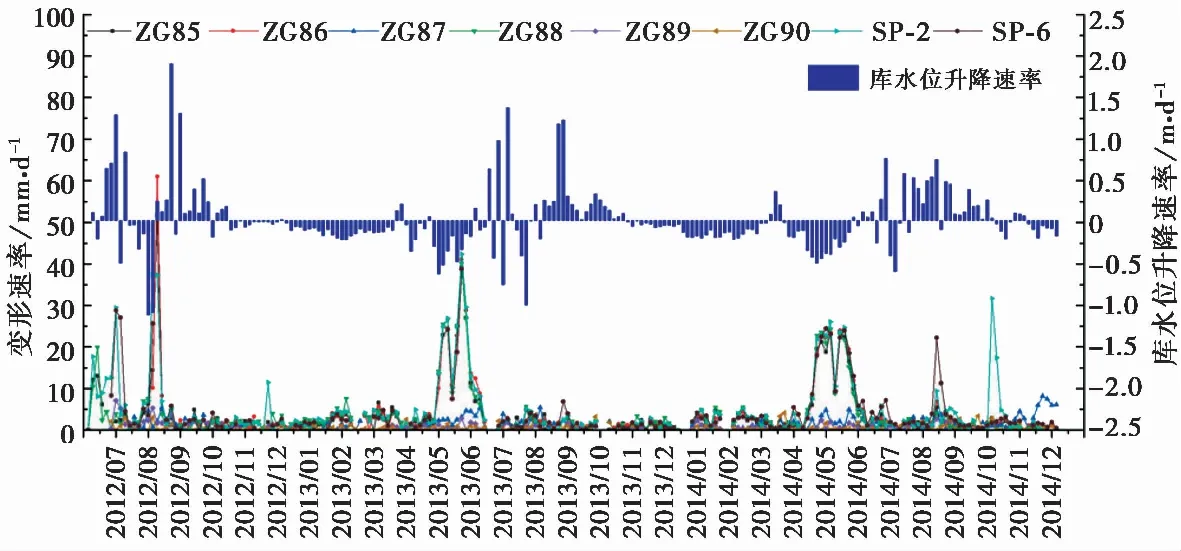
图3 树坪滑坡地表位移变形速率-库水位升降速率-时间关系
3 典型滑坡变形滞后时间分析
3.1 树坪滑坡变形滞后效应整体分析
由于各位移监测点所处于滑坡体空间位置不同,在滑坡整体位移变形中所占权重大小不同。因此,利用层次分析法,对ZG85、ZG86、ZG88和SP-2共4个监测点进行两两重要程度分析,并进行赋值,得到判别矩阵A为:

(7)
求解矩阵A的特征值,由此可知判别矩阵A的最大特征值为λmax=4.1256,λmax>n,为保证判定矩阵A准确性,为此需要检验其是否达到“满意一致”的程度(邓雪等, 2012)。
一致性指标CI:
(8)
一致性率CR:
(9)
式中:RI为随机一致性指标,可按表3选取(邓雪等, 2012)。

表3 随机一致性指标RI
计算得CR=0.047<0.1,于是判别矩阵A通过了一致性检验。再采用几何平均数估计各因素权重。
(10)
经计算可得权重向量为:
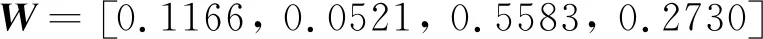
(11)
随着三峡水库蓄水过程的逐渐完成,树坪滑坡体的安全储备逐渐降低,并于2014年8月开始应急治理, 2015年6月全面竣工完成。为了计算结果更加直观明显,故选取治理之前的监测数据。因选取的3个时间段内总降雨量分别为10.1mm、141.4mm和64.2mm,降雨量较小,所以本文不考虑降雨这一影响因素。利用集对分析方法分别计算出仅在库水位下降的情况下滑坡变形滞后时间,具体步骤如下:
(1)对树坪滑坡2012年监测数据进行观察分析,在8月1日至8月21日库水位与滑坡位移相互关系较明显,库水位由160.25m下降至146.12m,平均下降速率为0.7m·d-1,即库水位平均下降速率阈值p=0.7m·d-1,规定波动范围为±0.1 m·d-1。因此,库水位下降速率在0.6~0.8m·d-1之间为平稳下降; 库水位下降速率大于0.8m·d-1为加速下降; 库水位下降速率小于0.6m·d-1为减速下降。
为考察滑坡位移滞后响应,位移数据选取2012年8月1日至8月31日数据,步长为1d等间距位移时序共计31组数据,该时间段内滑坡位移变形平均速率为3mm·d-1,即平均变化速率阈值q=3mm·d-1,规定滑坡位移变形速率在2~4mm·d-1之间为平稳上涨; 滑坡位移变形速率大于4mm·d-1为加速上涨; 滑坡位移变形速率小于2mm·d-1为减速上涨。
按照表1 判别同异反关系,并搜索不同平移步数下的同一度a。将绘制出的同一度与平移步数关系曲线进行二次多项式拟合,如图4 所示。以此判断当step为2步时,同一度a达到最大值,此时滑坡位移与库水位相关性达到最大。

图4 2012年同一度与平移步数关系
根据库水位下降对滑坡变形滞后时间公式T=step·Δt,计算滞后时间为2d。
(2)对树坪滑坡2013年监测数据进行观察分析,在5月10日至6月11日库水位与滑坡位移相互关系较明显,库水位由160.17m下降至146.26m,平均下降速率0.43m·d-1,即库水位平均下降速率阈值p=0.43m·d-1,规定波动范围为±0.1m·d-1。因此,库水位下降速率在0.33~0.53m·d-1之间为平稳下降; 库水位下降速率大于0.53m·d-1为加速下降; 库水位下降速率小于0.33m·d-1为减速下降。为考察滑坡位移滞后响应,位移数据选取2014年5月10日至6月20日数据,步长为1d的等间距位移时序共计42组数据,该时间段内滑坡位移变形平均速率为4.4mm·d-1,即平均变化速率阈值q=4.4mm·d-1,规定滑坡位移变形速率在3.4~5.4mm·d-1之间为平稳上涨; 滑坡位移变形速率大于5.4mm·d-1为加速上涨; 滑坡位移变形速率小于3.4mm·d-1为减速上涨。
按照表1 判别同异反关系,并搜索不同平移步数下的同一度a。将绘制出的同一度与平移步数关系曲线进行二次多项式拟合,如图5 所示。以此判断当step为5步时,同一度a达到最大值,此时滑坡位移与库水位的相关性达到最大。

图5 2013年同一度与平移步数关系
根据库水位下降对滑坡变形滞后时间公式T=step·Δt,计算滞后时间为5d。
(3)对树坪滑坡2014年监测数据进行观察分析,在5月6日至6月4日库水位与滑坡位移相互关系较明显,库水位由160.03m下降至147.34m,平均下降速率0.44m·d-1,即库水位平均下降速率阈值p=0.44m·d-1,规定波动范围为±0.1m·d-1。因此,库水位下降速率在0.34~0.54m·d-1之间为平稳下降; 库水位下降速率大于0.54m·d-1为加速下降; 库水位下降速率小于0.34m·d-1为减速下降。为考察滑坡位移滞后响应,位移数据选取2014年5月6日至6月14日数据,步长为1d的等间距位移时序共计42组数据,该时间段内滑坡位移变形平均速率为4.2mm·d-1,即平均变化速率阈值q=4.2mm·d-1,规定滑坡位移变形速率在3.2~5.2mm·d-1之间为平稳上涨; 滑坡位移变形速率大于5.2mm·d-1为加速上涨; 滑坡位移变形速率小于3.2mm·d-1为减速上涨。
按照表1 判别同异反关系,并搜索不同平移步数下的同一度a。将绘制出的同一度与平移步数关系曲线进行二次多项式拟合,如图6 所示。由图像可发现,同一度拟合曲线出现两个峰值,由此判断,在该时间段内出现了两次变形滞后响应,故需要分段考虑。又因第一次滞后响应受前面数据的影响,所以本文只考虑第二次滞后响应。因此,当同一度a第二次达到最大值时,相对平移步数为4,此时滑坡位移与库水位的相关性达到最大。
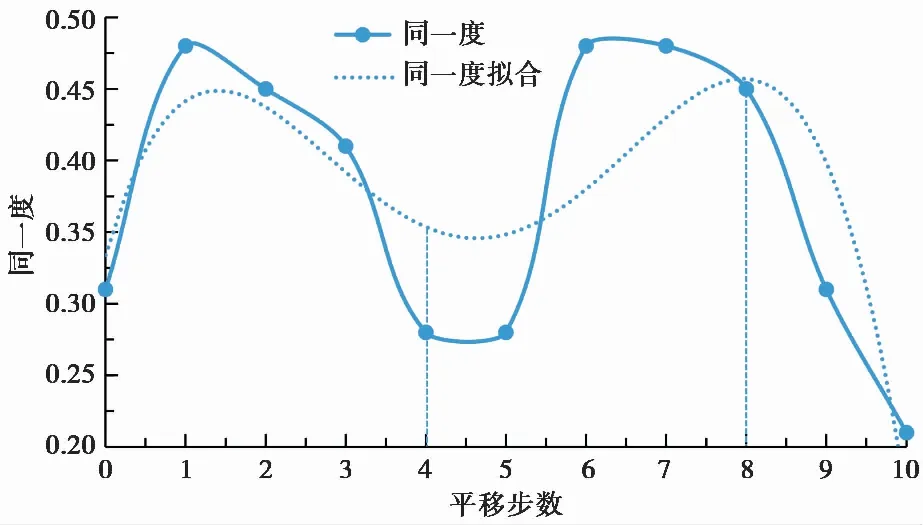
图6 2014年同一度与平移步数关系
根据库水位下降对滑坡变形滞后时间公式T=step·Δt,计算滞后时间为4d。
将2012年、2013年、2014年计算得到的滑坡变形滞后时间与相应时期库水位平均下降速率绘制成图表(表4、图7)。仅对树坪滑坡,当库水位下降速率小于等于0.43m·d-1时,滑坡变形滞后时间大于等于5d; 当库水位下降速率在0.43m·d-1到0.7m·d-1之间时,滑坡变形滞后时间在2d到5d之间; 当库水位下降速率大于等于0.7m·d-1时,滑坡变形滞后时间小于等于2d。因此,随着库水位下降速率不断增大,滑坡变形滞后时间不断缩短。造成这种现象的原因是:当库水位下降,产生向外的渗流,由于坡体渗透性较差,地下水排出缓慢,导致坡体内孔隙水压力增加,有效应力减小,降低了滑坡的稳定性(尚敏等, 2019; 汤明高等, 2019)。这与向玲等(2014)研究的结论“树坪滑坡库水位下降速率越快,地下水位上凸现象越明显,稳定性系数减小越明显”相符。因此随着库水位下降速率越大,滑坡变形滞后时间越短。
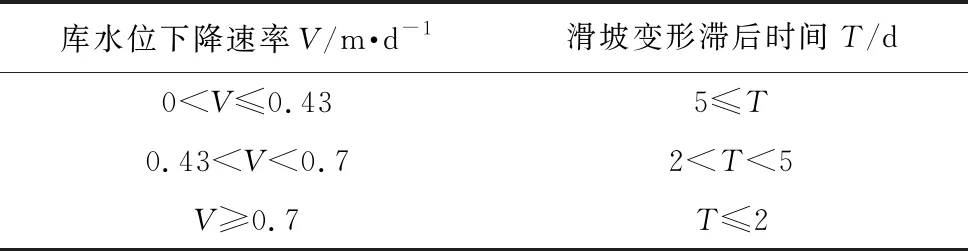
表4 库水位下降速率与滑坡变形滞后时间对应关系
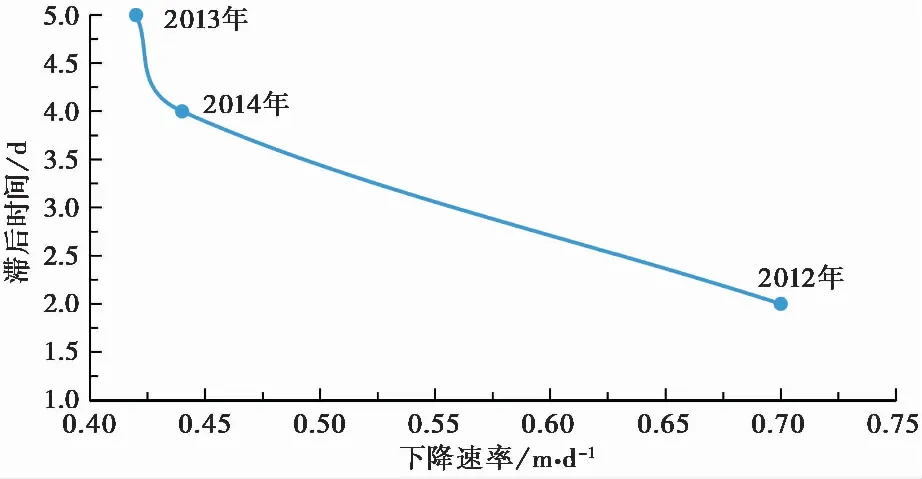
图7 库水位下降速率与滑坡变形滞后时间关系
为进一步验证,基于集对分析法计算出的滑坡变形滞后时间结果的实用性和准确性,现将理论分析结果与实际监测结果进行对比分析。
选取2013年5月10日至6月20日树坪滑坡自动监测点(ZG85、ZG86、ZG88和SP-2)的实际累积位移与库水位数据,绘制滑坡自动监测点累积位移-库水位-时间关系曲线如图8 所示。分析图像可知, 2013年5月13日至6月9日库水位快速下降,而累积位移在5月17日到6月14日之间急剧增大。因此,滑坡变形滞后于库水位的下降,本次滞后时间为5d左右,且与前文2013年相对应时间段内计算出的滑坡变形滞后时间基本吻合。
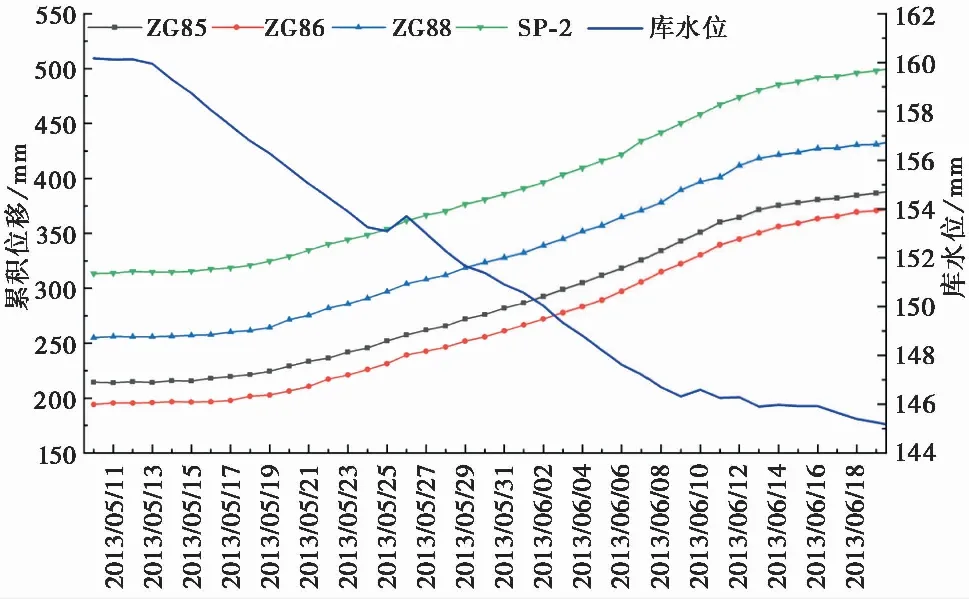
图8 滑坡自动监测点累积位移-库水位-时间关系
同样选取2014年5月6日至6月15日树坪滑坡自动监测点(ZG85、ZG86、ZG88和SP-2)的实际累积位移与库水位数据,绘制滑坡自动监测点累积位移-库水位-时间关系曲线如图9 所示。分析图像可知, 2014年5月6日至6月7日库水位快速下降,而累积位移曲线在5月10日之后陡然上升,滑坡变形加剧,到6月11日之后滑坡变形监测曲线趋于平稳。本次滑坡变形滞后于库水位下降的时间为4d左右,且与前文2014年相对应时间段内计算出的滑坡变形滞后时间基本吻合。
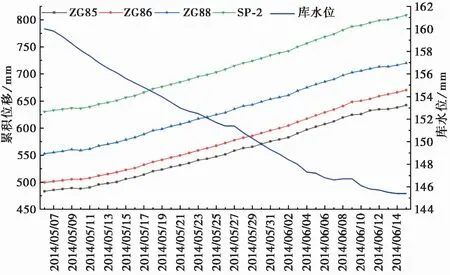
图9 滑坡自动监测点累积位移-库水位-时间关系
通过集对分析法计算滞后时间与监测数据图像分析的滞后时间相互验证,理论分析结果与实际监测结果吻合较好。若通过监测数据图像分析滑坡的变形滞后时间,需选取出大量数据绘制曲线图,才可观察出整体变化趋势,从而确定滑坡变形滞后时间。而集对分析法适用于短期滑坡变形滞后时间的计算,相对监测数据图像分析更方便简单。因此,运用集对分析法进行滑坡变形滞后时间的定量研究是可行的思路。
3.2 树坪滑坡不同空间位置的滞后时间分析
为考察在同一滑坡体中,库水位下降过程对滑坡体空间位置上变形滞后时间长短的影响,根据表5 选取4个监测点,分为主滑区中部监测点SP-2、ZG86和前缘监测点ZG88、ZG85。

表5 树坪滑坡专业监测点所处位置
利用上述数据运用相同的方法,按照滑坡加权位移-库水位同异反关系判别表,搜索不同平移步数下的同一度a。绘制同一度与平移步数关系曲线,并根据二次多项式进行拟合得到同一度拟合曲线。
由图10 可知,库水位以0.7m·d-1的速率下降,滑坡体前缘的变形滞后时间为2.4d,滑坡体中部的变形滞后时间为3.4d; 库水位以0.43m·d-1的速率下降,滑坡体前缘的变形滞后时间为5.4d,滑坡体中部的变形滞后时间为5.6d; 库水位以0.44m·d-1的速率下降,滑坡体前缘的变形滞后时间为4d,滑坡体中部的变形滞后时间为5.4d。
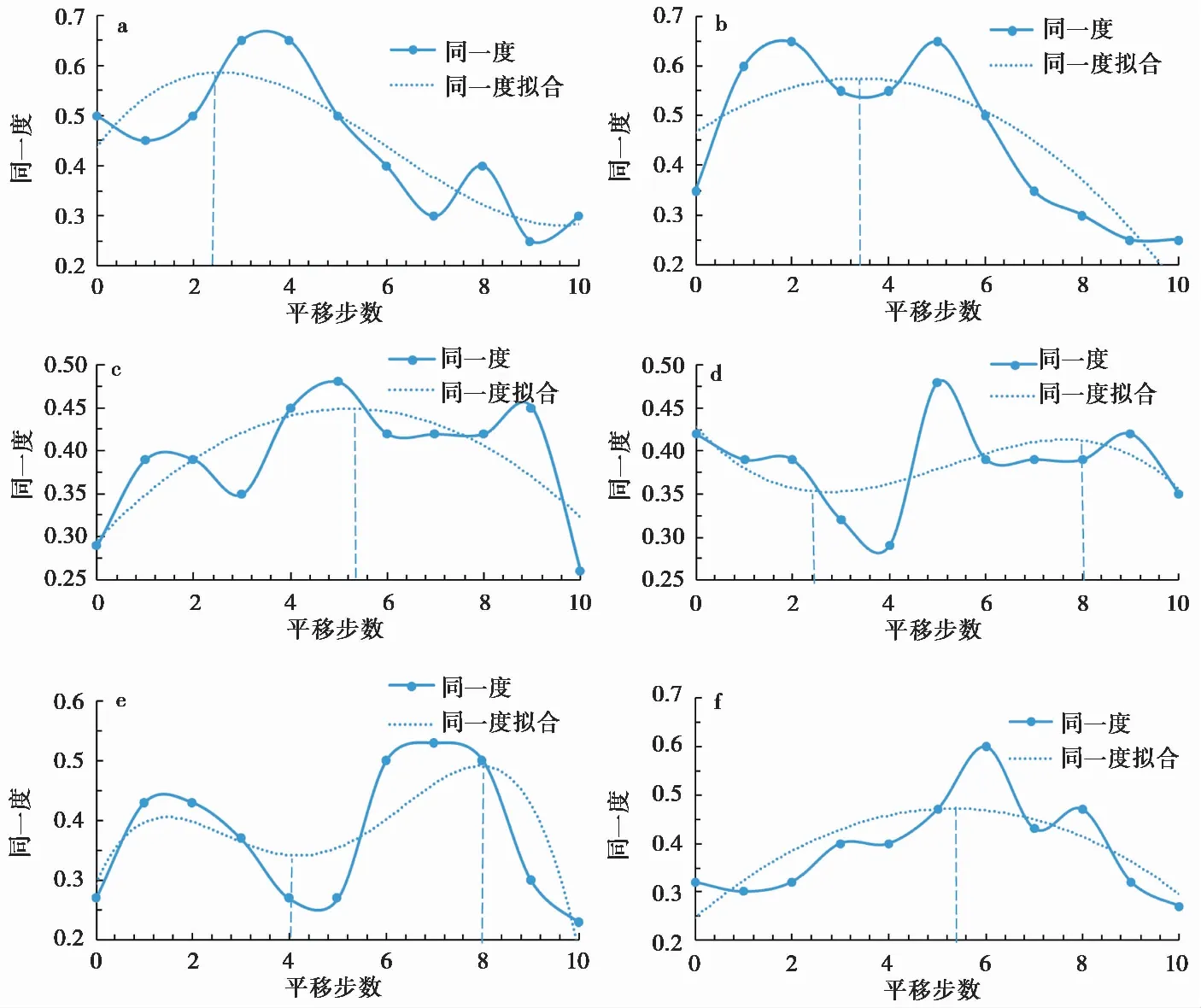
图10 不同空间位置同一度与平移步数关系曲线
综上可知,仅对树坪滑坡而言,如图11 所示,不同库水位下降速率对滑坡体空间位置上变形滞后时间影响特点为:越靠近滑坡体前缘变形滞后时间越短,当库水位下降速率在0.43m·d-1到0.7m·d-1之间时,滑坡前缘和中部的变形滞后时间差在0.2d到1.4d之间。
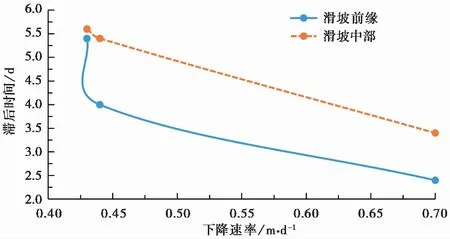
图11 不同空间位置上库水位下降速率与变形滞后时间关系
4 结 论
(1)通过滑坡加权位移的演化与库水位波动相互关系定性分析的基础上,寻找滑坡加权位移与库水位下降速率相关性达到最大时的平移步数,从而计算出滑坡变形滞后时间,且结果与实际情况相符。
(2)当库水位下降速率小于等于0.43m·d-1时,树坪滑坡变形滞后时间大于等于5d; 当库水位下降速率在0.43m·d-1到0.7m·d-1之间时,树坪滑坡变形滞后时间在2d到5d之间; 当库水位下降速率大于等于0.7m·d-1时,树坪滑坡变形滞后时间小于等于2d。
(3)以树坪滑坡为例,库水位下降过程对滑坡体空间位置上变形滞后时间影响特点为:越靠近滑坡体前缘变形滞后时间越短,当库水位下降速率在0.43m·d-1到0.7m·d-1之间时,滑坡前缘和中部的变形滞后时间差在0.2d到1.4d之间。
(4)本文没有考虑降雨因素对滑坡变形响应的滞后性,当降雨与库水位共同作用时需考虑降雨影响所占权重的大小,因此如何考虑降雨对滑坡变形滞后响应的影响还需进一步研究。
