一种非侵入式电梯运行状态智能监测方法

杨 昱，王千山，李雪鹏，许 增，李海芳

(太原理工大学 信息与计算机学院，山西 晋中 030600)

为了加强电梯质量安全工作，当前电梯行业正在大力推进按需维保。推进按需维保，首先要解决的问题是对电梯运行状态的监测。在实现状态监测的基础上才能进一步对电梯的健康状态进行估计与预测。

目前电梯行业中只有业内领先的少数电梯生产厂商如日立、奥的斯对自己生产的电梯有相应配套的电梯状态监测系统。它们采用的方式都是采集控制主板信号对电梯状态进行监测。目前对于电梯状态监测和故障诊断的研究中，采用侵入式方法的有：通过采集门控信号[1-2]对电梯门系统的故障进行监测与预测；通过监测马达电压[3]，挖掘其与电梯运行故障的关系；通过采集电梯控制芯片信号[4]进行远程监控；通过采集主板信号[5]使用数据挖掘分析多部故障电梯的故障信息与相关因素；采集电机编码信号以及调节器信号[6]，估计ISO 18738-1:2012标准描述的电梯关键性能指标。采用侵入式的方法需要考虑电梯的品牌，无法保证电梯的实际运行不受影响，并且需要专业技术人员安装，缺乏普适性。

当前研究中采用非侵入式方法的有：通过采集电梯的主要部件(轿厢、轴承、曳引机等)的振动信号[7-11]，进行故障的实时监测、分类与预警；陈志平等[12]结合了非监督学习与监督学习方法，通过提取电梯检验大数据中的振动数据进行故障的诊断与预测。SKOG et al[13]提出了一种易于安装的非接触式的电梯智能传感节点，通过对加速度的分析，跟踪电梯轿厢的位置，监测异常停止；郝真鸣等[14]在测量加速度信号的基础上增加了轿厢实时气压的测量，以监测电梯的运行位置与状态。

由于市场上电梯品牌繁多、运行时长、运行环境等客观因素的不同，每个电梯都有自己的正常运行模式，为了与所有电梯互操作而不用考虑其自身的传感器和控制系统，本文采用了非侵入式的方法。而目前的相关研究大部分实时性不能满足实际需求，需要安装信标才能解决长时误差积累问题。为此本文通过对加速度信号的分解、电梯加速度与速度的估计、传感器自动矫正、基于无迹卡尔曼滤波的信息融合，设计了一种不用安装信标、易于部署移动、普适性强且不影响电梯工作状态的实时状态监测方法。

1 方法总体概述

本文设计方法的主要部分如图1所示，通过加速度传感器和气压传感器采集数据。首先对两个传感器进行初始化，更新重力加速度和气压传感器的初始海拔。由于采集的加速度是三轴数据，通过Weiszfeld算法求中位中心进行重力加速度g的更新。在此基础上，通过更新的g将采集到的电梯轿厢加速度分解为重力方向和水平方向。重力方向的加速度即为轿厢运动方向的加速度，通过卡尔曼滤波结合电梯的运动特征，得到电梯加速度、速度的估计，同时根据水平方向的加速度信号进行振动分析，计算与基线的偏移以检测异常振动。同时使用融合SLAM的无迹卡尔曼滤波算法耦合加速度和气压传感器信息，对电梯的运行位置进行跟踪。最后将实时监测的信息通过Socket方式发送到赛尔网络IPv6云服务平台。云平台收到信息后，进行分析统计，并及时向电梯维保人员推送警报和维护策略，维保人员工作完成后向云平台进行反馈。

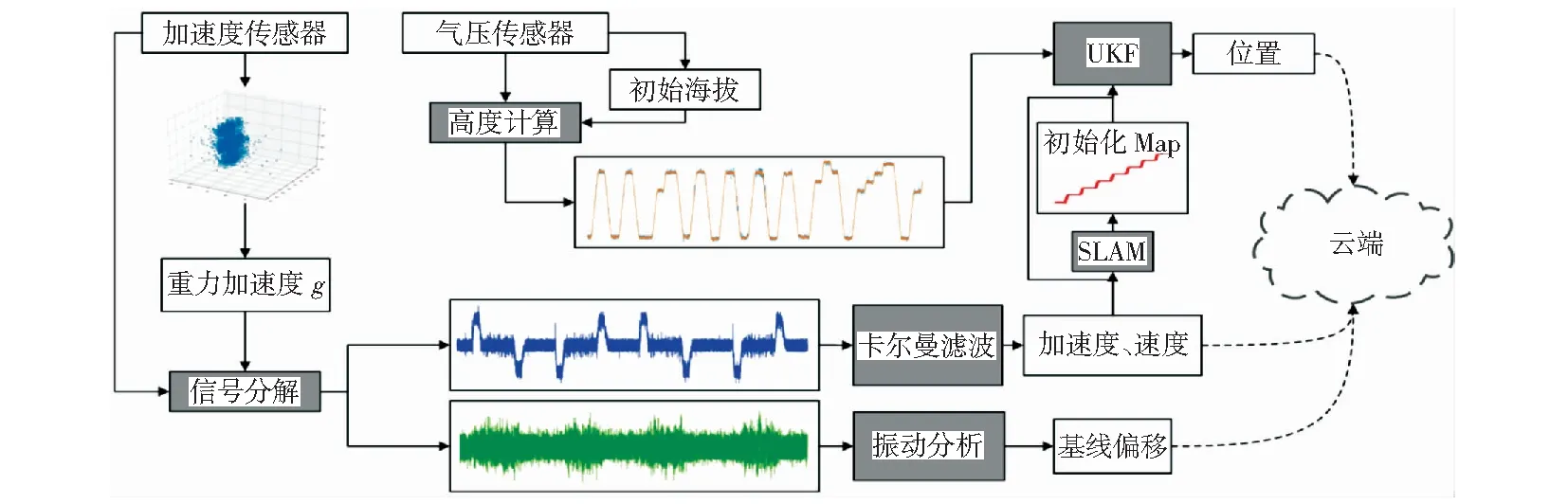
图1 方法概览Fig.1 Overview of the method

2 特征提取与预处理

2.1 传感器自动矫正

传感器的自动矫正包括初始化加速度传感器测得的重力加速度向量和气压传感器的初始海拔，以及根据电梯运行状态对二者进行自动更新。

2.1.1加速度传感器自动矫正

当系统刚开始运行(需要电梯处于静止状态)或运行中检测到电梯处于静止阶段时，采用滑动窗口(宽度为2 s，步长为0.5 s)处理所采集的三轴加速度数据序列，并根据所采集加速度向量的模过滤异常值；然后通过Weiszfeld算法求得所采集的三轴加速度数据的中位中心，即过滤后的所有加速度向量欧氏距离之和最小的点，以此作为初始化或更新后系统所使用的重力加速度向量。本文使用的Weiszfeld算法计算公式如下：

(1)

(2)

(3)

di(x,y,z)=‖(ai,bi,ci)-(x,y,z)‖ .

(4)

式中：m表示过滤后加速度向量的个数，(ai,bi,ci)表示过滤后的第i个加速度向量，(xk,yk,zk)表示Weiszfeld算法第k次迭代后求得的中位中心。将所有过滤后的加速度向量在各坐标轴上的均值作为初始点输入可以加快算法的收敛速度。

2.1.2气压传感器自动矫正

地球表面固定区域内的大气压在一定时间内随着海拔的不同而连续变化，通过测量气压计算高度变化的公式如下：

(5)

h=kALT-kALT0.

(6)

式中：kALT、p、p0分别为当前海拔、当前传感器测量气压、海平面气压，kALT0为基准位置的海拔。当系统刚开始运行(需电梯静止且位于基准位置)或在运行中检测到电梯处于静止阶段,通过气压传感器用滑动窗口的方式记录电梯当前的海拔序列，直到检测到电梯开始运动，使用的滑动窗口宽度为2 s，步长为1 s.3σ原则过滤记录海拔序列的异常值后，求平均值作为初始化或更新后的气压传感器的初始海拔。

2.2 加速度信号分解

将采集到的加速度向量减去重力加速度向量，通过内积运算将残差量分解到重力方向以及与重力垂直的方向。分解到重力方向的加速度信号即为电梯沿竖直方向(电梯实际运动方向)运动的加速度与噪音之和；分解到与重力垂直方向的加速度信号即为电梯在水平方向上的振动信号。加速度信号分解过程的计算公式如下：

Iresidual=I-g.

(7)

avertical=(Iresidual·g)/|g| .

(8)

Ivertical=avertical×g.

(9)

Ihorizontal=Iresidual-Ivertical.

(10)

式中：g表示重力加速度向量，I表示采集的三轴加速度，Iresidual为去除重力加速度后的残差量，avertical为重力方向的加速度分量的模，Ivetical为重力方向的加速度分量，Ihorizontal表示水平方向的加速度分量。图2为信号分解示例，图2(a)为源数据；图2(b)为分解后的数据，其中的竖线即为分解到重力方向的加速度分量。通过对加速度信号的分解与结合传感器的自动矫正，综合应用了加速度传感器测得的三轴数据，使用安装时不必关心加速度传感器Z轴的方向，可以增强系统的鲁棒性。

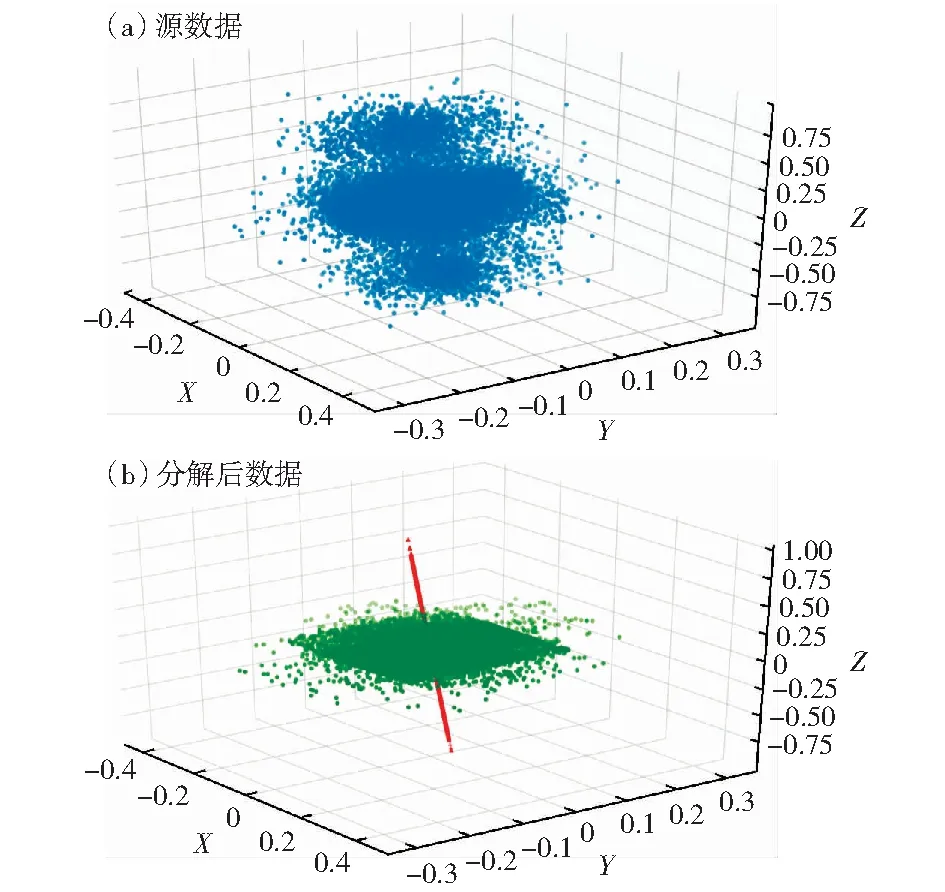
图2 信号分解示意图Fig.2 Signal decomposition diagram

3 电梯动力学特征估计

电梯的运动过程可以分为：静止阶段、加速阶段、匀速以及减速阶段。电梯运行过程中的加速度、速度特征如图3所示，理想状态下电梯在加速阶段与减速阶段，加速度的变化可近似划分为匀速增大、保持、匀速减小三个子阶段[6]。

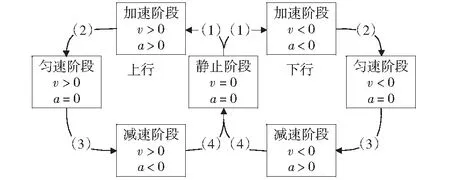
图3 电梯理想运动特征Fig.3 Ideal motion characteristics of elevator

由此可见，理想状态下，除阶段之间的过度点外，加速度的导数都维持常值。据此提出电梯理想运动的假设：

ak=ak-l.

(11)

通过公式(11)假设当前时间步的加速度的导数等于上一时间步的加速度的导数，简化电梯运动模型，则电梯的动力学特征可以用以下的状态空间模型来描述：

xk=Fxk-l+wk.

(12)

其中，

式中：x为系统状态向量，从上到下的元素依次表示速度、加速度、急动度；F为状态转移函数；dt为采样时间间隔；wk为零过程噪音向量，假设为零均值协方差Q的高斯噪音，Q与采样时间有关，状态向量xk的每个状态被假定为电梯运行过程中的平均值。

本文使用卡尔曼滤波，以加速度传感器实时的测量值通过信号分解得到的重力方向分量和时间戳作为输入，以系统状态向量x作为输出，通过预测步和更新步建立输入与输出之间的联系进行最优化估计，主要步骤如下：

1) 计算采样时间间隔dt，根据dt调整状态转移函数F和过程噪音协方差Qk，根据系统状态模型(12)预测下一时间步的状态，并估计系统协方差。

(13)

2) 估计系统协方差计算卡尔曼增益K，H为测量函数H=(0,0,1,0)T，R为测量噪音协方差。

(14)

3) 输入计算信息，即预测值与测量值的残差。

(15)

4) 用信息修正前状态预测值和协方差：

(16)

(17)

由图3可见，理想状态下，当电梯处于静止或匀速阶段时，加速度为零，考虑到传感器噪音与电梯运行中的过程噪音，为系统输入的重力方向分量设定观测窗口w=[averticalk-n+1,averticalk-n+2……averticalk]和阈值，averticalk表示当前的加速度，n为观测窗口宽度，当窗口内的所有的值都小于阈值时，将加速度矫正为0.当加速度为零时，电梯处于静止或匀速阶段。因此当加速度为零，速度的大小小于设定阈值时，可将速度矫正为零，同时可确定电梯处于静止状态，进行加速度传感器的自动矫正。

采用上述方法所监测到的加速度与速度特征示例如图4，从图中可以清晰看到电梯运行的4个阶段。

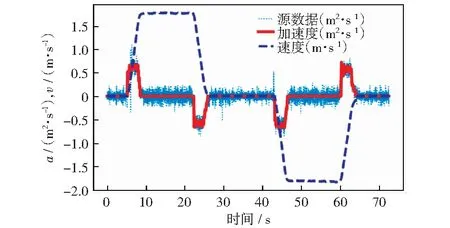
图4 加速度、速度估计示例Fig.4 Example of acceleration velocity estimation

4 电梯运行位置估计

4.1 状态转移函数

加速度传感器的短时精度高，但由于两次积分所产生的累积误差，对位移的估计误差会随时间不断累积，短期精度较高，但长期误差会增大到不可接受。而气压传感器对位移的估计误差累积相对较慢，可以将二者融合提高对电梯运行位置估计的精度。根据牛顿公式，k时刻电梯相对于参考层的运行位置hk可以表示为：

hk=hk-1+Bkuk+wk.

(18)

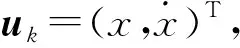
由于电梯特殊的运行机制，当电梯处于静止阶段时，轿厢相对于参考点的高度是一组固定的离散值。用列表Map进行描述Map@(h1,…,hi,hn)，其中hi指第i层相对于参考点的高度，n为电梯所能到达的楼层数。系统的状态转移函数可以表示为：

(19)

式中，δhi表示先验的测量误差。

4.2 Map初始化

利用加速度传感器短时精度高的特点，使用SLAM算法学习电梯的楼层位置[13]，对Map进行初始化，得到Map的先验信息。电梯需要顺序地跑完所有楼层(逐层停止)，通过卡尔曼滤波并结合电梯的运动特征，可以较为精准地估计两次停车间的距离，通过逐层扫描就可得到楼层间距与楼层高度。图5为实验场所一次Map的初始化过程(一层为参考层)，由图可见每两次相邻的停车之间，加速度和速度的变化都遵循相同的模式。楼层信息的初始化结果如表1，表中最后一列是在相邻楼梯间测得的实际楼层间距。楼层间距最大误差为0.03 m，平均误差为0.023 m.可见，通过SLAM算法能够较为准确地获得各楼层位置初始化信息，而整个过程实现了与电梯品牌以及安装场所的无关性。

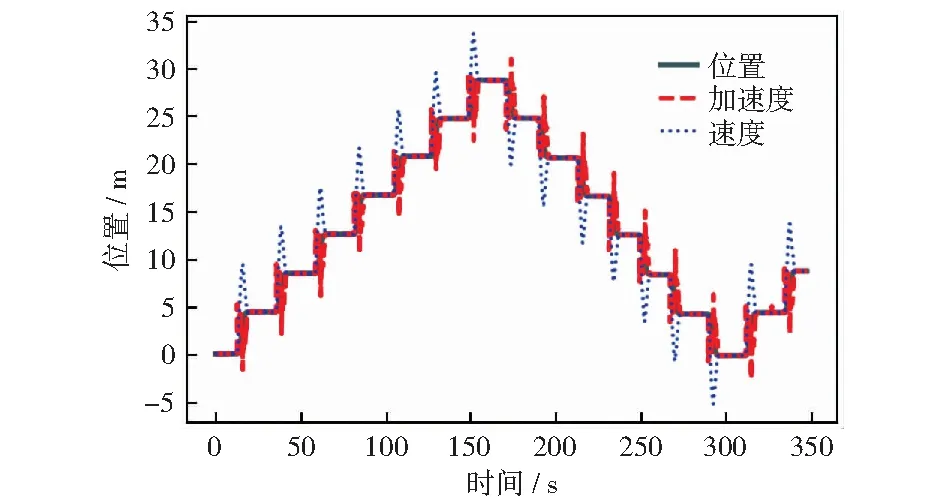
图5 Map初始化Fig.5 Map initialization

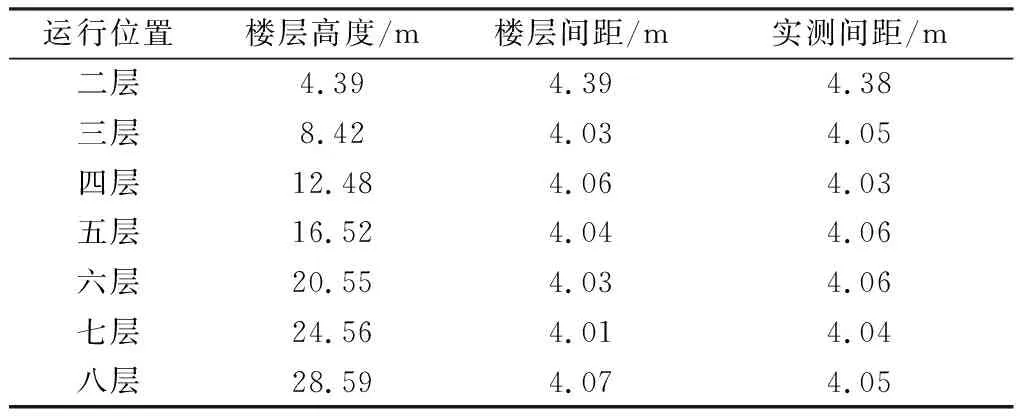
表1 楼层信息的初始化结果Table 1 Initialization results of floor information

4.3 无迹卡尔曼滤波

无迹卡尔曼滤波(UKF)计算量与扩展卡尔曼滤波同阶，至少可以达到二阶精度[15]。相较于扩展卡尔曼滤波，无迹卡尔曼滤波不需要知道状态转移函数和测量函数的具体表达形式，对函数的可导性不作要求。因此本文采用无迹卡尔曼滤波对电梯的位置进行估计。无迹卡尔曼滤波的核心是无迹变换[16](Unscented Transform)，通过确定性采样进行非线性变化来逼近非线性分布，无迹变换之后采用卡尔曼滤波计算框架进行状态更新。本文使用的UKF具体计算框架如图6所示。

由于系统的输入与输出含义相同且都为一维向量，本文采用简化的UKF计算公式。

首先采用对称采样策略，得到2n+1个采样点和对应的权重；将所有的采样点代入状态转移函数，将结果根据UT变换加权得到状态预测值和预测协方差。

系统的输入输出相同，所以不需要进行量测步的无迹变换，获得测量信息后根据测量值和测量噪音协方差计算信息和卡尔曼增益，然后进行状态估计值和对应协方差的更新。

本文采用了基于新息和过程噪音的自适应方法，设σ为P的平方根，当新息大于2σ，即预测值与观测值距离过远时，说明预测函数与噪声统计特性在这个时间步上与实际运动不适配，所以为Q增大一个固定值s，以增大卡尔曼滤波中测量值的比重。否则将Q减小s直到还原到初始值。之后判断当前电梯的运动状态，若电梯静止，根据Map检测当前位置所距最近的楼层hi，若hk∈U(hi,δh)则进行Map的更新并执行传感器自动矫正程序，否则表明电梯可能出现异常位置停车，发送异常停止警报。

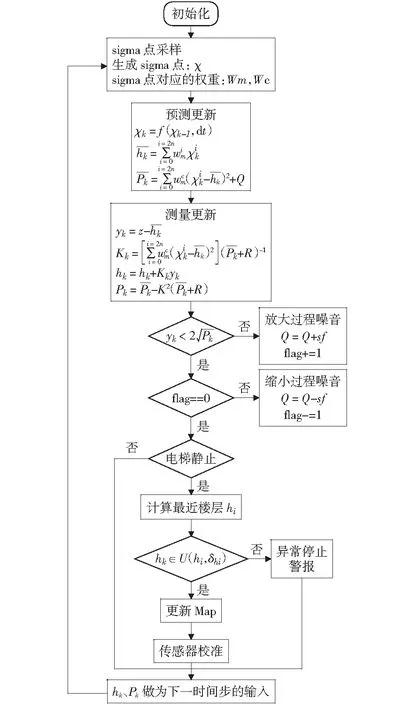
图6 UKF计算流程Fig.6 UKF calculation process

5 电梯振动分析

将电梯运行过程中轿厢的振动作为非侵入的监测电梯运行状态的重要特征进行提取。由于竖直方向的振动信号在加速和减速阶段包含了电梯运动的加速度，所以使用水平方向加速度信号检测异常振动。通过水平方向振动的能量确定代表电梯健康状况的基线；然后观察实时采集到的数据是否偏离基线。如果偏离，则表明电梯可能发生异常。本文所使用的基线生成的方法如下：

选取移动平均数(MA)为收敛的指标，n为已采集的信号数。

(20)

计算移动平均误差(EMA)，将相距m-1个点的斜率k做为中长期收敛指标。停止准则为k≈0.当满足停止准则时完成收敛，如未收敛则继续采集数据计算k值。

EMAj=|MAj-MAj-1|/MAj-1×100 .

(21)

k=atan((EMAn-EMAn-m)/(xn-xn-m)) .

(22)

完成收敛后，将所记录的水平振动能量的均值μ作为基线，并计算标准差σ.根据统计学原理，将μ+3σ划为警戒线，建立判别模型，进行在线监测。将采集的新数据输入判别模型，进行状态检测。

6 实验结果与分析

本文搭建了树莓派3B+搭载GMP180(气压传感器)与MPU6050(加速度传感器)的硬件平台，传感器BMP180采用超高线性模式，采样频率为39.2 Hz.MPU6050选取测量范围为±2g，采样频率为200 Hz.两个传感器分别绑定了树莓派CPU的一个内核，采用多进程运行方式保证其数据采集的并行执行。选取信计学院北楼电梯作为本文的实验环境(楼层信息见表1)，对本文方法的性能进行了验证。

图7为试运行中对试验电梯的加速度特征和速度特征的估计结果，结合加速度特征与速度特征对电梯运行方向与所处运动阶段(图3所述)的检测，正确率可达百分之百。其中图7(a)、图7(b)显示了根据《电梯技术条件(GB/T 10058-2009)》计算的质量参数：试验电梯每次运行的最大加速度、最大减速度、以及a95(95%采样数据的加减速度)。其中，速度的运行区间为[-1.91,1.80]，最大加减速度均小于1.5 m/s2，加减速度a95均大于0.5 m/s2，符合国家标准。根据《电梯技术条件(GB/T 10058-2009)》计算的质量参数能够反映电梯系统的健康状态，也可用作电梯预测性维护的数据特征。

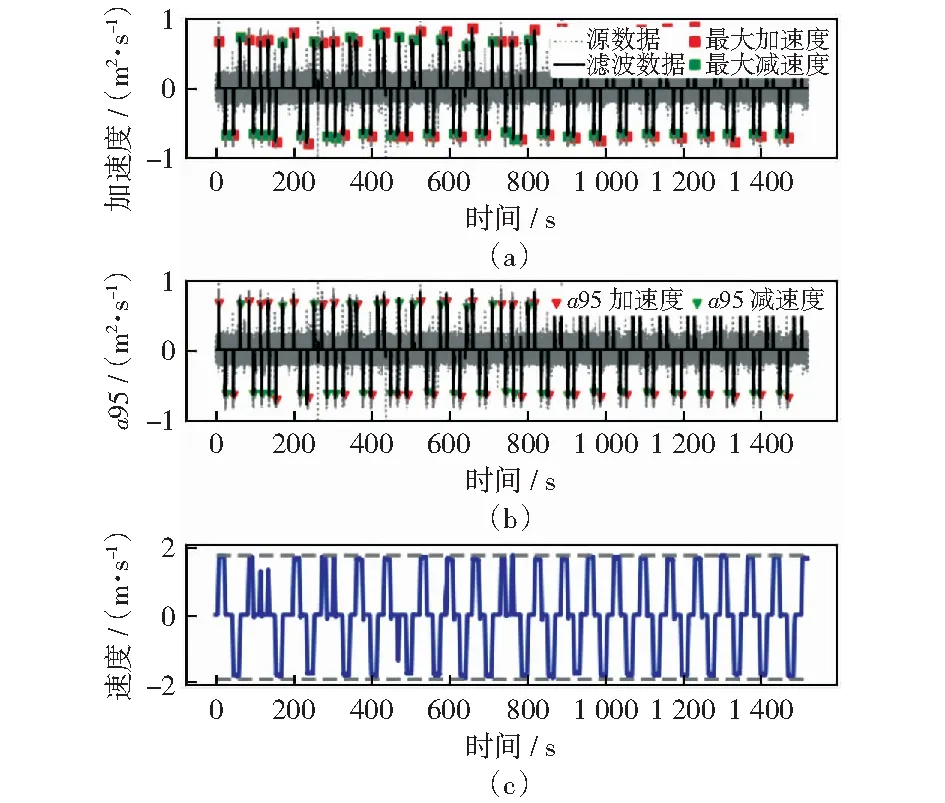
图7 电梯运动特征估计结果Fig.7 Estimation results of elevator motion characteristics

通过无迹卡尔曼滤波将两种传感器的信息进行融合对电梯运行位置的跟踪示例如图8所示。

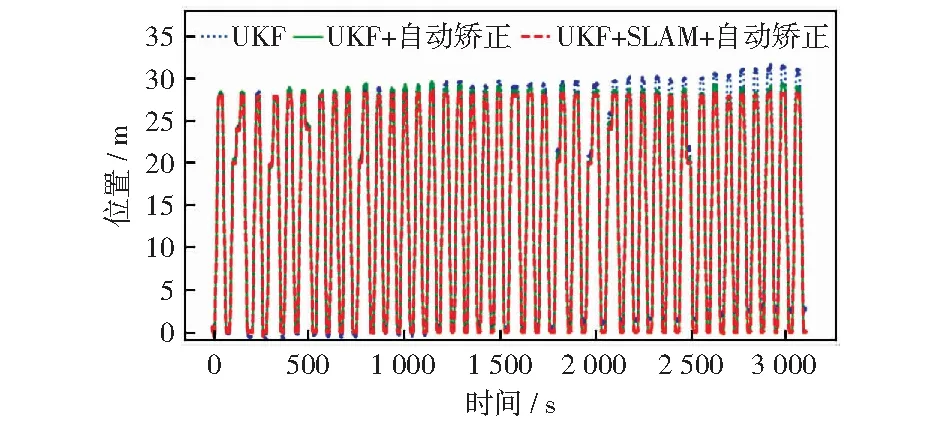
图8 电梯位置跟踪示例Fig.8 Example of elevator position tracking results

由图8可见，由于UKF算法不能及时矫正由测量所积累的误差，导致误差累积越来越大，随着运行时间的增长，UKF算法的状态估计明显偏离真实状态。在UKF算法中，引入传感器自动矫正机制后，累积误差得到了很好的控制，长时状态估计性能提升明显。而结合SLAM算法对状态转移函数进行优化后，对电梯的运行位置进行了进一步矫正，更好地减小了UKF状态估计的误差。

实验中位置跟踪的具体误差分析可见图9：由误差累积概率分布图可知，融合自动校准和SLAM的UKF算法能够有效控制误差的积累，位置的平均误差为0.098 m，均方根误差为0.143 m，(如表2所示)，收敛更快，有更高的滤波精度。本文设计的方法基本解决了位置误差的累积问题，能够更好地估计电梯的运行位置。

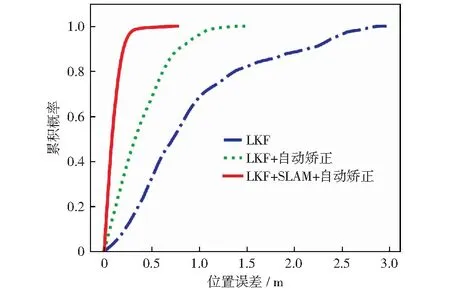
图9 位置误差累积概率分布图Fig.9 CDF of position error

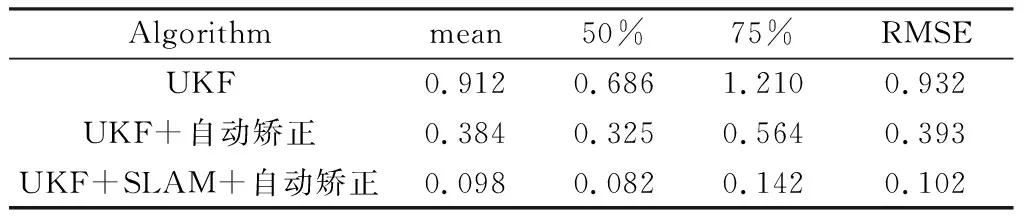
表2 电梯位置误差Table 2 Elevator position error m

当电梯的曳引系统出现问题以及导轨的错位和变形会导致振动能量的异常增大，获得电梯实时加速度和位置的基础上，可以建立电梯振动能量位置谱图，以反映电梯的工作状态。为了排除电梯加速减速阶段，轿厢自身加速度的干扰，采用水平方向的加速度信号建立振动能量位置谱。通过在电梯运行过程中进行大幅度的跳跃来模拟电梯曳引系统或导轨系统出现问题的情况[14]。分别在电梯运行的上行加速阶段、上行匀速阶段、上行减速阶段、下行加速阶段、下行匀速阶段、下行减速阶段进行了大幅跳跃，结果如图10.图中竖轴为电梯运行位置，横轴为对应位置的振动能量，虚线为采用基线生成算法训练生成的警戒线(0.150 m4/s2).谱图中的尖峰即为模拟产生的异常振动，可见在电梯运行各个阶段均可清晰检测出模拟故障的发生，并可定位故障发生时轿厢所在位置，为电梯系统的维修保养以及被困人员的解救提供重要信息。

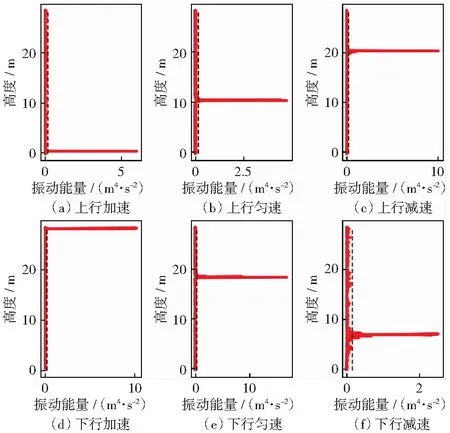
图10 振动能量位置谱Fig.10 Vibration power versus position spectra

通过以上对电梯运行加速度、速度、位置、振动实时精准的监测，可以有效地检测电梯曳引系统异常、平层故障、导向系统故障并准确定位导轨错位变形位置，还能预防电梯冲顶和墩底事故的发生。

7 结束语

本文实现了对电梯运行状态和位置的实时监测，通过加速度信号的分解、传感器的自动矫正并结合电梯的运动特征使用卡尔曼估计了电梯的动力学特征，并计算了《电梯技术条件(GB/T 10058-2009)》的相关质量参数。使用融合SLAM算法的无迹卡尔曼滤波器进行了位置跟踪，解决了位置误差累积的问题。在实际的电梯运行环境下进行了测试，在不安装信标的情况下平均定位误差为0.098 m.本文对电梯的加速度水平分量进行振动分析，建立电梯运行的基线与振动能量位置谱，并通过模拟故障进行了验证。本文设计的非侵入式电梯状态监测系统成本低廉、安装移动简单方便、即插即用、普适性强，和电梯自身的控制系统完全脱耦，不会影响电梯的控制和使用。未来的工作中，本文计划研究电梯门系统的检测功能，在已知故障的电梯中进行实验并进一步进行故障分析。