基于改进引导滤波和双梯度信息的多聚焦图像融合
2021-11-24刘梦瑶
刘梦瑶,周 诠
(西安空间无线电技术研究所 空间微波技术国家级重点实验室,西安 710100)
0 引言
多聚焦图像是由不同的聚焦区域,在相同的场景下拍摄的一系列图片,具有冗余和互补的特性。由于硬件设备和成像条件的局限性,采集到的图像信息可能无法满足分辨率、信息量等方面的需求,而多聚焦图像融合能够把从不同空间或时间上获得的多个来源的信息进行合并或集成,以得到有关实体、关系或事件的更完整、更精确、更可靠的信息或推论。
目前,多聚焦图像融合算法主要分为三种类型:基于空域的方法[1-3]、基于变换域的方法[4-7]和基于深度学习的卷积神经网络方法[8]。基于空域的融合算法可以直观地通过局域像素关系来确定聚焦区域,主要是通过对图像的纹理特征进行定义,在精确提取出纹理特征后,计算边缘特征的空间、频率、能量、梯度等参数,作为聚焦区域的判定标准。因此,图像纹理、边缘的准确提取和聚焦区域判定的标准是基于空域的多聚焦图像融合算法的关键。
引导滤波作为一种自适应线性滤波的方法,能够准确地提取图像边缘信息,因此,有部分学者使用引导滤波作为图像特征提取方法,应用于图像融合算法中[9-10]。自2013年Li[11]首次使用引导滤波的方法进行多聚焦图像融合后,部分学者提出了多种改进的引导滤波方法:Kou[12]通过局部方差加权来设定线性平滑的权值,可以得到更加清晰的物体边缘。谢伟[13]通过联合梯度信息对平滑系数进行加权,能够在一定程度上减弱平滑后的光晕现象。郭剑桥等[14]在引导滤波中加入了内容感知因子,但图像的细节处理效果有待提高。李健等[15]为提高多聚焦图像的融合性,加入了高频自带系数,使图像信息更丰富。
基于能量、梯度和方差的聚焦区域判定标准广泛应用于基于空域的融合算法和基于变换域的融合算法中。三种判定指标各有利弊:区域能量可以很好地反应图像信息的丰富程度。但是细致纹理区域的能量值可能低于平坦区域,导致聚焦与离焦区域判定错误;方差考查图像块的像素波动情况,虽然能够标定像素值波动的区域,但是边缘的损耗较大;梯度对边缘的变化程度敏感,是判定聚焦与否的重要参数。但是,梯度算法只考虑到系数的变化程度,容易造成图像低频有用信息的缺失。其中,梯度信息由于能够更精确地判定物体边缘,广泛应用于多聚焦图像的融合算法中。
有部分学者对基于梯度的判定准则进行了优化。姚权等[16]将梯度、方差和能量信息进行结合,对图像的高低频Haar小波变换系数分别进行处理,融合效果优于单一判断标准的融合算法。杨桄等[17]针对各层曲波系数的特点,采用基于像素和基于区域特征加权的融合算法得到高频系数,并将梯度特征自适应加权方法得到图像的低频系数,融合效果优于平均的融合方法。方帅等[18]使用梯度加权对每层图像系数进行融合,并使用图像的自相似性来补充高频细节,避免各层融合比例差距较大导致失真。
从之前的研究可以看出,引导滤波是优秀的保边滤波方法,但是需要优化参数来提升物体边缘提取的质量;梯度信息作为聚焦区域的判定标准,常应用于基于变换域的图像融合方法,但是常需要辅助其他信息共同判定。针对上述融合算法的局限性,本文提出一种基于改进引导滤波和双梯度信息的多聚焦图像融合算法,能够有效提取聚焦区域中的平坦区域的边缘特征,抑制离焦区域的边缘细节,提高部分聚焦图像的纹理提取效果,同时优化聚焦区域的判定结果,从而提升多聚焦图像的融合质量。
1 相关研究
1.1 基于引导滤波的图像融合
引导滤波是根据图像局部的相关性,使用自适应的滤波核进行滤波的具有良好保边性能的滤波模型[11]。该模型假设,对于图像的某个邻域中的每个像素来说,其滤波输出的结果和该像素相关的局部引导图像是线性关系,其中的线性系数则由输入图像和引导图像共同决定。
对于输入图像I来说,输出的滤波图像O是引导图像P在以像素位置p为中心的局部窗口w中图像的线性变换。即
Ow=apPw+bp
(1)
式中,线性变换系数ap和bp由最小二乘法根据输入图像Ii和引导图像Pi得到,其代价函数为:
(2)
则对应的ap和bp分别为:
(3)
(4)
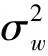
基于引导滤波的初始分割图生成流程由图1所示:使用不同的引导图像来进行二次引导滤波,这两次滤波结果的差值用来提取源图像的细节特征并生成初始分割图。首先使用原始源图像作为一次引导滤波的引导图像,得到的滤波结果作为二次引导滤波的引导图像,最终得到源图像的边缘特征图Ae为:
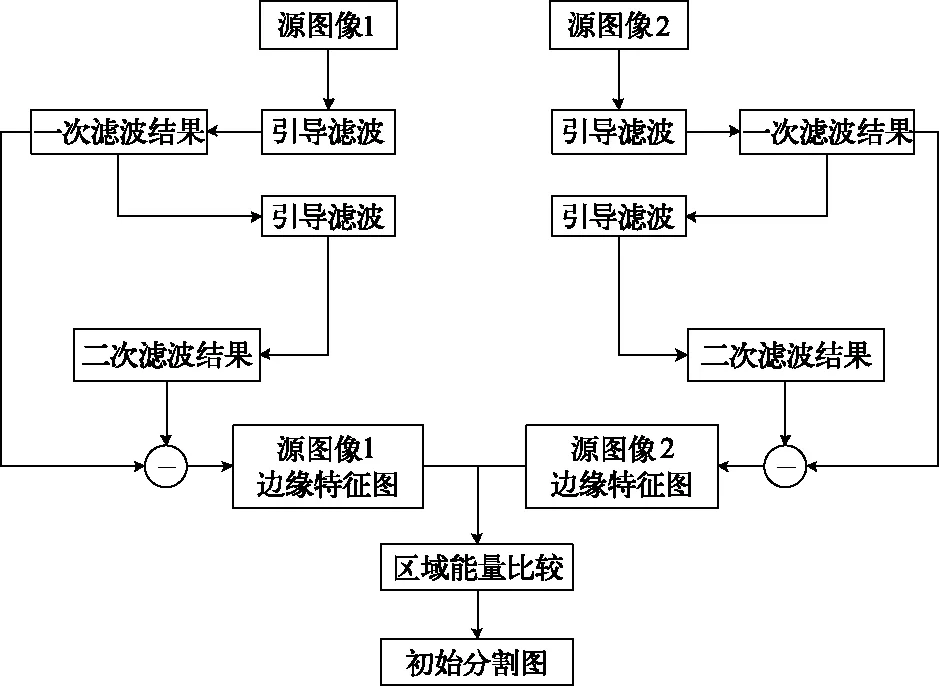
图1 传统基于引导滤波的初始分割图生成
Ae=fg(A,A)-fg(A,fg(A,A))
(5)
式中,fg(A,A)表示以A为输入图像,且以A为引导图像的引导滤波的结果;fg(A,fg(A,A))表示以A为输入图像,以fg(A,A)为引导图像的引导滤波结果。
图2为传统的引导滤波提取图像特征值的仿真结果,可以看出在使用不同引导图像时,引导滤波可以对边缘信息进行不同程度的平滑,由此来提取图像的纹理部分。但是,聚焦区域的平坦部分在经过两次滤波前后改变不够大,不能够被提取出来,有可能会导致分类错误,例如下图中的红色框部分。而且对于某些纹理较复杂的图像块,即使处于离焦区域,在经过两次滤波后,改变也是非常大的,所以也可能会被错认为是聚焦区域,例如下图中的黄色框部分。

图2 二次引导滤波结果及滤波差值结果
引导滤波之所以能够有效地提取出聚焦区域的边缘,抑制离焦区域的边缘,是来自于不同程度的滤波结果之差。但是,将图像进行了平滑操作后,会进一步缩小聚焦区域和离焦区域的像素差异,导致聚焦与离焦区域不易区分。然而,不同程度的平滑图像之间的差值必然小于聚焦区域和离焦区域之间的差值,基于这个思想,本文提出了一种结合高斯滤波的改进引导滤波算法,通过增加聚焦区域像素灰度值与离焦区域像素灰度值之间的差异来提高聚焦区域的定位精度。
1.2 基于梯度信息的图像融合
图像的梯度信息可以描述像素灰度值的变化剧烈程度,是多聚焦图像融合中判定物体边缘强弱的常用参数标准。融合算法可以通过参考不同尺度下图像变换域系数的梯度信息来判定聚焦区域。对于图像块w来说,假设其以(x,y)为中心,尺寸为m×n,则该像素点(x,y)的平均梯度[16]为:
G(x,y)
(6)
式中,I(x,y)是像素点的小波变换系数。图3为以Haar小波为小波基,分解2层的小波系数在计算梯度信息后的仿真结果。

图3 小波系数维度的梯度信息
以往的算法通常将基于梯度的聚焦区域判定准则应用于小波、剪切波等变换域系数[16],可以看出由于系数方向的不完整性,系数梯度无法准确描述物体边缘。因此,本文对基于空域的梯度信息进行分析。
图4和图5为像素灰度值维度下的梯度信息示例。可以看出,相比较于变换域系数维度下的梯度信息来说,像素灰度值作为梯度测量维度时,聚焦区域的图像边缘和纹理处对局部梯度信息有极大响应,可以更清晰地描述物体的边缘和纹理。

图4 像素维度的梯度信息
由图4(c)、(d)可以看出,物体边缘周边的细小纹理处,两张源图像的梯度有明显差别,聚焦区域的梯度信息可以更细致地描述整个聚焦物体的边缘和内部纹理。但是,由图5可以看出,虽然两幅图像块的梯度信息极大值是相同的,为64。但是均为花盆中明暗交界明显的物体边缘,也就是说,物体的关键边缘无法通过两幅源图像的梯度值区别来进行判定,需要辅助其他的信息,否则很难将聚焦区域判定准确。
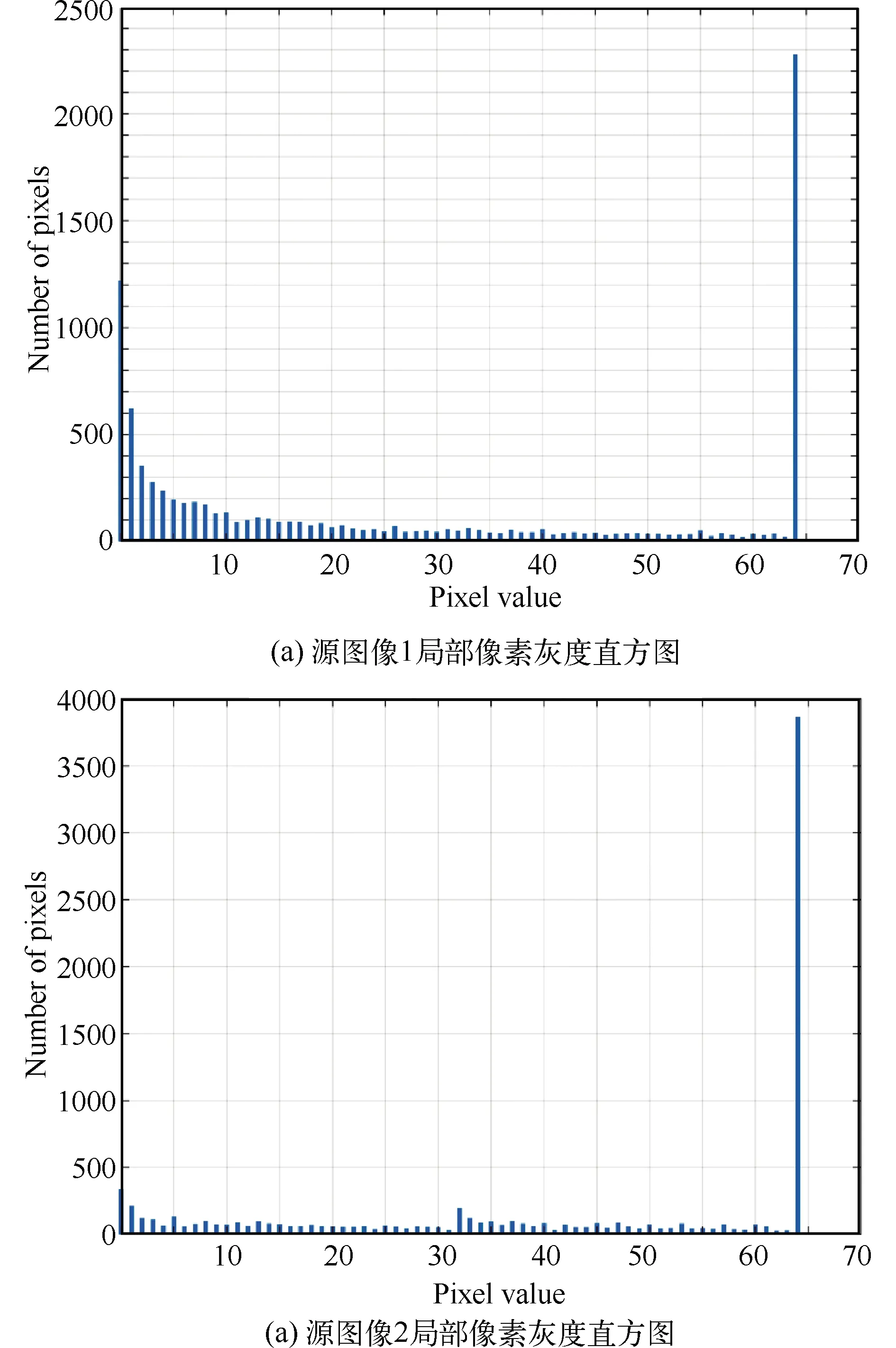
图5 源图像局部的像素个数直方图
由此,为了能削弱模糊边缘对梯度信息造成的干扰,我们可以同时借助图像的边缘特征作为梯度的另一个测量维度,因为边缘特征已经将较平滑区域进行了筛选,去除了相关干扰,因此可以使得聚焦物体边缘更容易被提取出来。基于上述两节的分析,我们提出了结合双梯度信息的改进引导滤波图像融合算法。
2 算法流程
针对引导滤波提取图像边缘信息流程上的固有缺陷,和梯度信息无法有效区分离焦与聚焦区域的物体边缘的特性,我们提出了基于改进引导滤波和双梯度信息的多聚焦融合算法。该算法打破了传统的滤波结果相差分的流程,增强了图像的边缘特征,对聚焦区域的平坦部分也能够极好地保留下来,同时结合源图像与边缘特征图的梯度信息,优化聚焦区域的特征边缘,能够生成分区精确的区域分割图,根据分割图即可对多聚焦源图像进行融合。结合双梯度信息的改进引导滤波多聚焦融合算法的具体流程如图6所示。本节将对算法的每个步骤进行详细说明。
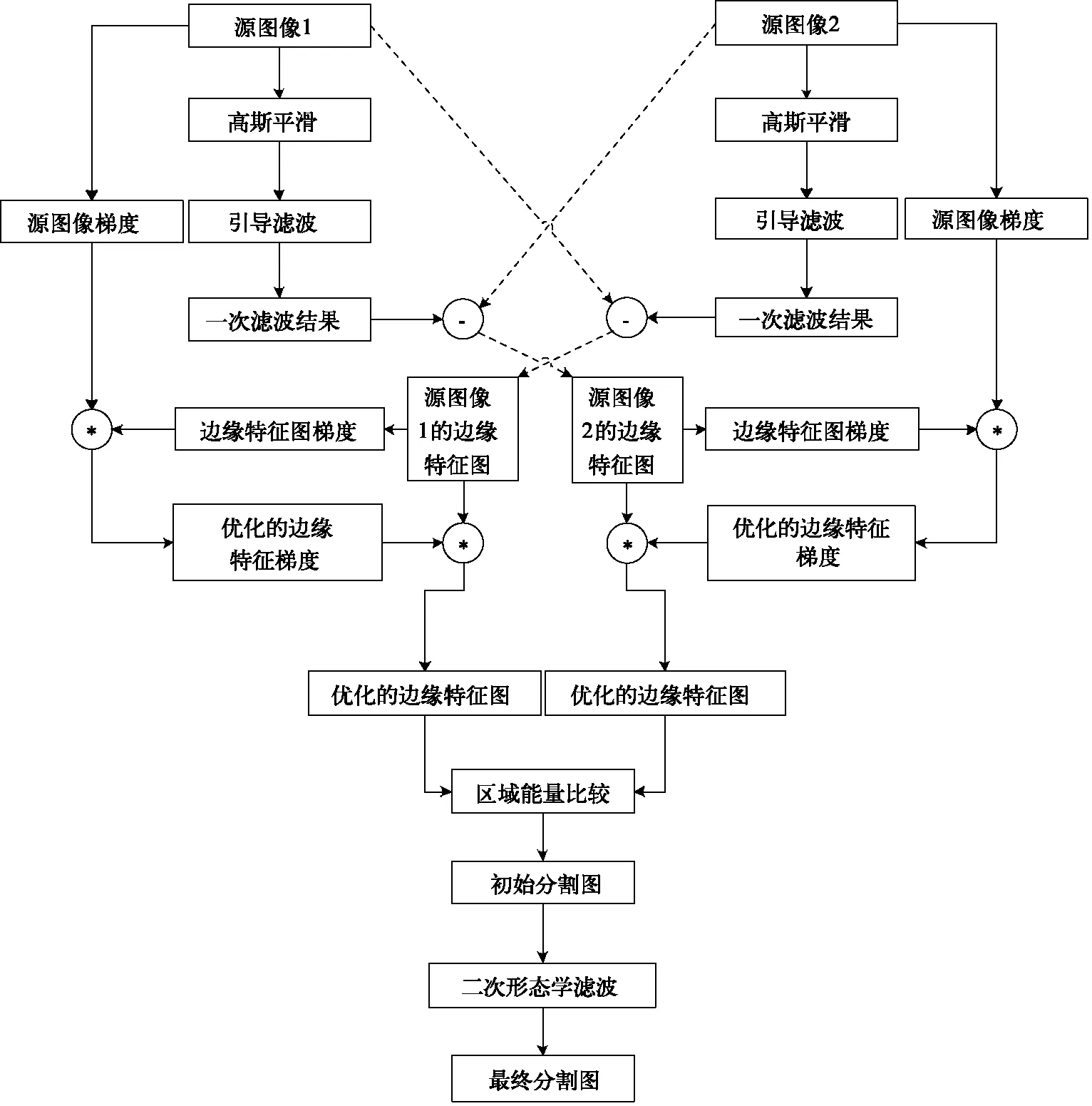
图6 结合双梯度信息的改进引导滤波融合算法流程图
2.1 结合高斯滤波的改进引导滤波
由1.1节分析结果可知,物体边缘的差值会因为引导滤波的平滑操作而减小。所以我们需要尽可能地增强离焦与聚焦区域关于物体边缘的差异,尽可能减小结构清晰物体对区域分割的影响。基于这种思想,我们提出了使用源图像代替引导图像进行差分提取特征的改进引导滤波算法。
部分聚焦的源图像1在引导滤波操作后,离焦区域变得更加平滑,我们使用另一幅部分聚焦的源图像2与其做差,从而保留了源图像2更显著的物体边缘特征。由于源图像1的离焦区域几乎是源图像2的聚焦区域,因此源图像1的离焦区域在平滑后,和源图像2的聚焦区域差距更大,特征提取更加明显;同时,源图像1的聚焦区域在平滑后,和源图像2的离焦区域差异变小,因此可以抑制进一步这部分像素的干扰。如此得到的结果优于同一张源图像进行2次引导滤波并差分之后的结果。
为了进一步增加离焦区域和聚焦区域的差异,我们对部分聚焦图像进行高斯模糊,再进行引导滤波,这样对离焦区域可以进一步平滑,对聚焦区域进一步抑制,能够更加突出图像的聚焦区域特征。可以看出,高斯平滑且引导滤波的源图像1可以看做是源图像2的结构部分,源图像2通过对结构部分进行差分,得到聚焦区域的纹理特征图,源图像1的纹理特征图同理可得。由此,多聚焦图像的纹理特征图分别为:
M1=A1-f(g(A2),g(A2))
(7)
M2=A2-f(g(A1),g(A1))
(8)
式(7)中的f(g(A2),g(A2))为以g(A2)为输入图像和引导图像的引导滤波结果;式(8)中的f(g(A1),g(A1))为以g(A1)为输入图像和引导图像的引导滤波结果;g(A1)、g(A2)分别为A1、A2高斯滤波的结果。M1为源图像1的边缘特征图,M2为源图像2的边缘特征图。
图7(c)、(f)为基于改进引导滤波的边缘特征图结果,可以看出,本算法不仅可以有效地提取出小字母和条纹图像块,桌面倒影的部分也能够提取出来;并且可以有效地提取出前景的物体,桌面边缘这种较平滑的聚焦区域也能够正确判定。

图7 改进引导滤波的图像边缘特征图
2.2 结合双梯度信息的初始分割图生成
在得到源图像的边缘特征图之后,我们需要准确地划分源图像的聚焦区域。从1.2节分析可得,图像特征维度下的梯度信息是常用的聚焦区域判定参数,而像素值维度下的梯度信息也可以对聚焦区域的判定提供一定的参考。基于此,我们提出结合像素灰度值和边缘特征值的双梯度分割图生成算法。
由图8(a)、(b)可以看出,源图像聚焦区域的物体边缘相对于离焦区域来说,线条更清晰且和周边像素对比度更明显。图8(c)、(d)为源图像的边缘特征图,可以看出,物体形状明显的离焦区域会被提取出来,但是特征边缘是模糊的,同时,聚焦区域的特征边缘是清晰的,且较为连续。

图8 源图像与其边缘特征图
接下来我们分别对图像灰度值和边缘特征图进行局部梯度信息的计算。局部范围w均为3×3,公式如式(6)所示。
图9为两幅源图像边缘特征图的梯度,可以看出,在不连续的离焦特征边缘处,梯度信息是不连续的,因为它的边缘特征值是由光晕产生的,光晕本身是模糊且不连续的,导致其梯度也是模糊不连续的。而对于聚焦区域,图像边缘特征图的梯度可以准确地判定物体边缘形状,是由于聚焦区域的边缘特征值梯度由清晰的物体边缘提取。

图9 源图像边缘特征图的梯度
计算源图像的梯度信息如图10所示。可以看出,对于聚焦区域来说,源图像的梯度可以指示物体边缘范围,因为清晰边缘和纹理对梯度的响应是很大的。对于离焦区域来说,源图像的梯度只在物体的最显著的边缘处响应较大,其他细致纹理等区域响应均极小,由此可以清晰地区分源图像的离焦区域与聚焦区域。

图10 源图像的梯度
因此将源图像边缘特征图梯度和源图像的梯度进行结合,可以作为初始分割图的辅助判定依据。
由此,我们通过源图像的梯度来确定边缘特征图的梯度范围,再根据优化后的边缘特征图梯度来生成初始分割图。
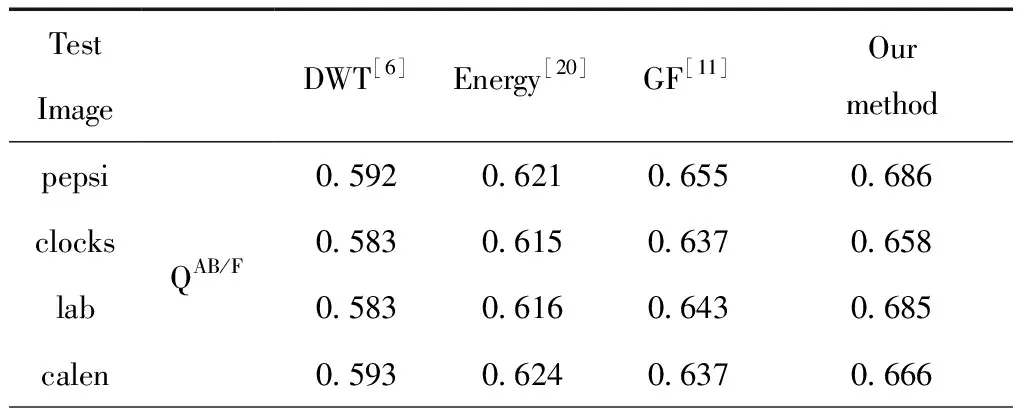
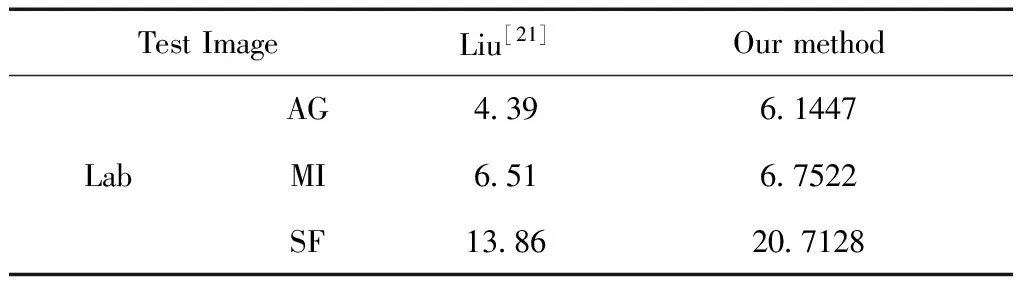
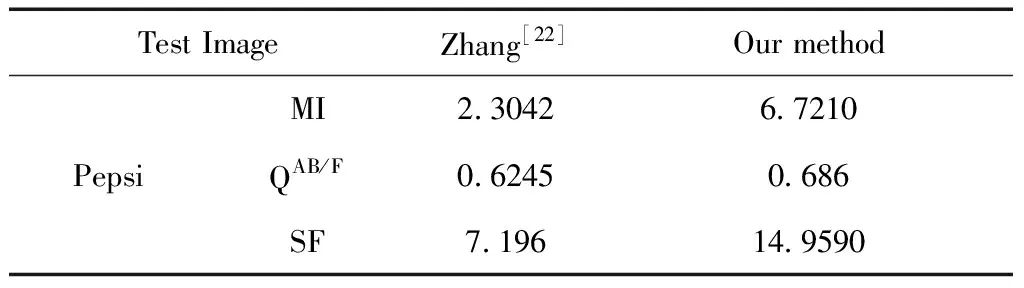
令U1和U2分别为两幅源图像的梯度图,W1和W2分别为两幅源图像边缘特征图的梯度图。若U1(i,j)>U2(i,j),则W1(i,j)保留,令W2(i,j)=0;若U1(i,j) 图11 优化后的边缘特征图梯度T1、T2 再将梯度差异图与各自的边缘特征图进行点积,得到优化后的边缘特征图H1、H2,然后使用基于能量的区域判定准则来确定初始分割图。 初步分割后,我们通过闭运算来消除分割图中的孔洞,并平滑分界线。但是初始分割图中的部分孔洞较大,如果使用更大的结构元素进行操作,可能破坏部分边缘特性,所以将膨胀和腐蚀分别进行两次,这样可以有效地消除物体形状内部的孔洞,并且保持物体的图像边缘,从而得到最终分割特征图。 为了验证本文所提算法的可行性与有效性,本节选用4组多聚焦灰度图像组作为测试图像,从主客观两方面进行评价。测试图片均来自标准多聚焦融合图像集Lytro Multi-focus Dataset[19],测试图像均已经经过精确配准。 对比算法中,我们选择经典的基于小波变换的融合算法[6]、基于引导滤波的多聚焦融合算法[11]、基于区域能量的加权融合算法[20]作为对比算法。这三种算法为现在多聚焦融合图像算法[21-25]中优先采用的对比算法。因此,本节我们选取这3种经典多聚焦融合算法进行对比研究,并对本文算法的性能进行主观和客观分析。 我们选用Pepsi、Clocks、Lab、Calendar这4组多聚焦灰度图像组作为测试图像,下面分别对每组图像在不同算法下的融合结果进行主观层面的分析。 (a)、(b)组分别为源图像。 (c)组为基于小波变换的融合方法,可以看出重构的融合图像边缘会存在部分伪影,导致整个融合图像的物体边缘都不清晰。视觉效果不佳。 (d)组为基于区域能量的加权融合算法,可以看出,对比度较大的物体边缘和平坦又模糊的边缘,都会出现分区错误的现象。 (e)组为基于引导滤波的融合算法,存在由于像素灰度扩散导致的分区错误的问题。 (f)为本文算法结果,可以看出,本文算法在保持了引导滤波融合算法优势的同时,能够正确地提取出光线不足、纹理灰度对比度较小的区域特征,并进行正确分区。融合效果优于其他的3种算法。 从以上测试图像组的结果可以看出,虽然引导滤波对比传统的基于空域、变换域的融合算法,能够更准确地划分多聚焦图像的聚焦与离焦区域,但是对于平坦区域和对比度较低的纹理区域,无法通过滤波结果差值来有效提取特征。本文算法通过增大弱纹理的对比度差异,使得引导滤波差值能够更好地提取物体边缘特征,同时结合梯度信息消除边缘特征图中的光晕,能够有效提升引导滤波算法的融合质量。 本文选取边缘梯度算子QAB/F、互信息MI、结构相似度SSIM、空间频率SF作为算法评价指标。边缘梯度算子通过度量融合结果包含的图像边缘信息量来评估融合的性能,值越大表明融合图像保留源图像的边缘信息越多,融合效果越好;互信息量表明了源图像和已融合图像之间的信息传递情况,值越大表明有越多信息量从源图像传递至融合图像;结构相似度表明2幅源图像与已融合图像的结构相似之和,值越大说明融合效果越好;空间频率表明图像灰度的变化率,空间频率越大表示图像越梯度越大,边缘越清晰。表1为几种算法的评价指标结果。 表1 4组测试图像的客观评价指标对比 从边缘梯度算子这个指标项中可以看出,本文算法可以更加精确地选择像素边缘对比度高的区域作为融合结果,因此本文算法的效果更加优于其他算法的融合效果。 从互信息这个指标项中可以看出,基于小波的融合算法由于影响了高频系数的相关性,部分像素灰度值有所变化,融合图像中保留的来自源图像的信息量是最少的;基于区域能量加权算法需要加权的部分较少,因此信息量保留较多;基于引导滤波的算法区域划分也较为准确,因此指标优于基于能量加权的算法;本文算法可以更好地保留源图像的信息量,指标优于其他三种对比算法。 从结构相似度这个指标项中可以看出,本文算法略优于其他三种对比算法。说明更能够保持源图像和已融合图像的灰度分布的一致性。 空间频率属于评价图像空间水平和垂直梯度的指标。clocks组的基于区域能量加权的空间频率最高,是因为基于区域能量加权的融合结果中有部分纹理融合错误,导致边缘线条增多,梯度较大。本文算法保留的聚焦区域纹理较多,因此空间频率指标高于其他三种对比算法。 为了更加客观地分析本文算法的融合结果,我们对数据集Lytro Multi-focus Dataset中的全部27组图像进行对比测试。这27组图像包含了纹理较多的图像、不规则结构较多的图像、平坦区域占比较大的图像等等,且其中聚焦区域和离焦区域的模糊程度差异多样,涵盖了多聚焦图像组的各种情况。对比算法采用经典的基于小波变换、区域能量加权、引导滤波的融合算法,评价指标采用边缘梯度算子QAB/F、互信息MI、结构相似度SSIM、空间频率SF。测试结果如图12所示。图中,x轴代表测试图像序号。 图12 各算法对4组测试图像的结果 从图13可以看出,本文算法的融合效果比较稳定,对于所有的测试图像,本文算法均有一定程度优于传统算法。本文的平均边缘检测算子指标为0.6725,平均高出小波变换算法0.1164,高出区域能量算法0.0572,高出引导滤波算法0.0276,说明本文算法对物体结构边缘的提取和融合有较好的效果;结构相似度的平均值为2.3216,高出小波变换算法0.5322,高出能量加权算法0.2569,高出引导滤波0.1393,说明本文算法和引导滤波均能够较好地保持图像边缘和结构,而本文算法对于不明晰的结构边缘仍旧有极好的提取效果;空间频率优势不明确,因为基于能量加权的算法可能会因为梯度反转而融合出错误边缘,从而增加空间频率;从互信息量指标来看,本文算法的平均互信息量为4.9276,本文算法的互信息量平均高出小波变换2.1357,高出能量加权0.7692,高出引导滤波0.3524,说明本文算法可以有效地保留源图像信息量。 图13 数据集所有图像的客观指标对比结果 从上面实验分析结果可以看出,本文算法对于纹理较多的图像、不规则结构较多的图像、平坦区域占比较大的图像均能较好地提取物体边缘,更精确地划分出聚焦区域与离焦区域,有较好的融合结果。 为了进一步说明本文算法的融合效果,本文选择与近年发表的改进多聚焦融合算法[21-22]进行部分客观指标的对比。本文与文献[21]共同使用了Lab图像进行算法融合效果测试,且共同使用互信息量MI、空间频率SF作为客观指标,为了更全面地对比客观指标上的差异,本文另计算了测试图像的平均梯度AG进行指标比对。表2列出了两种算法针对测试图像Lab共同使用的客观指标对比,可以看出,本文算法能够更好地保留源图像的信息量,对于细致纹理保留效果更好,因此互信息量和平均梯度的指标较高。 表2 Lab测试图像的客观评价指标对比 本文与文献[22]共同使用了Pepsi图像进行算法融合效果测试,并且都使用互信息量MI、边缘检测算子QAB/F、空间频率SF作为客观评价指标。表3列出了两种算法针对测试图像Pepsi共同使用的3类客观指标对比。可以看出,本文算法能够更好地保留源图像的信息量,边缘信息保留的更加完整,保留细节更多,空间频率更高。 表3 Pepsi测试图像的客观评价指标对比 本文提出一种结合双梯度信息的基于引导滤波的多聚焦图像融合算法。本算法采用改进的引导滤波提取源图像边缘特征,可以在提升聚焦与离焦图像边缘特征差异后,使得边缘纹理效果更加明显,从而更精确地提取出图像的各种纹理信息;其次,根据源图像和边缘特征图的梯度的不同特性,可以削弱高对比度大面积的离焦区域图像对分割区域准确度造成的影响,从而进一步精确确定边缘特征图中聚焦区域的范围。实验方面,现有文献中大都只用了Lytro Multi-focus Dataset数据集中的4组数据,统计意义不足,而本文使用了该数据集中全部27组数据,研究结果更有普遍性和统计意义。因此,从实验结果可以看出,本文算法融合效果的主客观评价明显优于其他算法。
2.3 二次形态学滤波
3 实验结果与分析
3.1 算法测试结果的主观分析
3.2 算法测试结果的客观分析


4 结论
