气垫船动力学ACVSIM模型的初步验证（二）

W. Milewski, B. Connell, B. PetersenD. Kring

气垫船动力学ACVSIM模型的初步验证（二）

W. Milewski, B. Connell, B. Petersen1
D. Kring2

（1Applied Physical Sciences Corporation，2Flight Safety Technologies, Inc.）

孙新 编译

人们对改进气垫载具的耐波性动力学预测能力重新产生了兴趣。这导致了第一原理数值模拟模型ACVSIM (Milewski等人，2007)的发展，该模型集成了气垫和裙摆动力学模型与基于高阶样条的流体动力学边界元模型。本文概述了ACVSIM最近的改进，以及使用2007年秋季获得的基线深裙作为模型尺度的LCAC进行初始验证研究的结果。该仿真工具提供了研究设计修改的影响的能力，以及模型载具缩放问题与多耦合物理系统的问题。

表1总结了这两种自由度模型在没有阻尼的情况下预测的固有频率。还列出了气垫和自由表面刚度的估算值。在本例中，我们选择了1/12的缩放比例，以与NSWCCD模型测试的缩放比例一致。从此分析中有几个关键的观察结果。首先，对于两种配置，造波和气垫模式的频率基本上是不耦合的，因为它们相差一个数量级。气垫在模型规模上比自由表面要硬一些，因为两种情况下的气压都相同。其次，气室固有频率在模型尺度上极高，并且不太可能被入射波激发或在载具刚体运动中观察到。在全尺寸下，入射波有可能激发腔模，因为其工作弗劳德数(Froude number)相对较高，因此波遇到的频率相对较高。最后，造波模的固有频率标度为标度比的平方根的倒数，与弗劳德标度一致，而空腔固有频率标度近似为标度比的倒数。

表1 使用两个DOF集总参数模型预测的1/12th尺寸和全尺寸ACV的无阻尼固有频率

阻尼的适当值很难用第一流体原理来确定，因为物理通常是非线性的，或者需要用高保真模型进行昂贵的计算。

对于在自由表面上工作的ACV，阻尼系数的估计可以从模型试验数据确定。例如，与裙边和缓冲供气系统相关的阻尼可以从刚性表面上的自由衰减实验中得到。类似的，在自由表面上工作的ACV的自由衰减试验提供了波阻尼的估算。波浪阻尼也可以通过使用势流模型的自由衰减试验的数值模拟来确定。

3 ACVSIM的气垫模型

ACV缓冲层内的气压产生了支撑载具的力，它是运动动力学中的一个主导项，与流体动力自由表面响应、结构变形以及裙袋和手指的接触力一起产生作用。两个因素会影响载具上的气垫力：1）空间和时间的气压变化，2）气垫的几何形状定义了有效的压力中心，并提供了在侧倾和俯仰时的恢复力(Milewski等，2007年)。压力还直接取决于几何体积和流动间隙。

在本节中，将介绍适用于各种运行条件的几种不同模型的气体定律和流量连续性条件。几何形状的非线性处理，裙部变形的细节以及ACV运动方程的解，提供了裙部与波浪之间的几何形状，体积和间隙区域，以及解决气压所需的波动。

除了可以分成多个隔间的气垫外，还考虑了其他隔间。这些腔室可包括例如在提升风扇和袋室下游的气室，其孔口模型限定了腔室之间的压降。提升风扇的特性也包括在内，以消除不稳定的风扇影响，例如流动惯性和体积容积。静态提升风扇特性曲线将压头与风扇流量相关联。额外的非稳态处理可实现更逼真的风扇效果，例如迟滞现象。

第一个气垫模型是符合密封垫体积的基本绝热气体定律，而不考虑风扇的流入和裙边的流出。与更先进的气垫模型一起使用时，该模型可用于隔离气垫的首次共振，并隔离孔口和提升风扇的效果。

接下来的两种方法，从静态模型开始，增加了对连续性条件，节流孔和对提升风扇特性的影响。静态公式仅对稳态平衡问题严格有效。但是，它也已被实现为时域ACV动力学的准静态模拟（Yun和Bliault，2000年）。可以看出，与包括孔口阻尼和不稳定风扇特性的更完整的动态公式相比，这种特殊的准静态方法往往会错过一些重要的惯性和阻尼特性。

第三种方法实现了用于流动连续性的非稳态动态公式，以将随时间变化的压力，体积和ACV运动与节流孔阻尼和非稳态风扇效应相结合。这种方法紧跟开发用于设计和分析气垫着陆系统的方法（Captain等，1975）。

第四种方法基于三维波动方程的解。尽管先前的三个公式将每个隔室中的压力建模为空间均匀，但此公式捕获了整个气垫中的空间和时间压力变化。使用沉浸边界方法（Immersed Boundary Method ，IBM）在固定的规则网格上以载具平均前进速度平移求解控制方程式（Milewski等，2007年）。IBM是ACV模拟的理想选择，特别是当几何被非线性处理并且可以自由移动和变形时。

基本的三维波动方程模型的一个局限性在于它不能说明空气流入或流出垫子的情况。在第五种建模方法中，通过将流动连续性模型与基本的三维波动方程模型相叠加，克服了这一限制。

已采用这五种方法来研究关于模型实验和全面操作经验的不同近似水平的物理有效性。简单的模型可能适用于广泛的工作条件。但是，它们不太可能完全捕获升沉，俯仰和横摇之间的耦合，也不大可能对ACV的大振幅波和运动有效。使用IBM解决三维波动方程的高级模型是对气垫动力学的一种新颖处理。这种方法可以捕获先前工作中尚未分析的耦合流体动力和高阶缓冲模式。这些空间变化的压力效应可以帮助解释和解决诸如“鹅卵石”共振效应之类的问题。

3.1 捕获气泡绝热模型

最简单的模型基于理想气体定律和绝热假设。该用于多方压力-密度关系的控制方程式本身是准静态的，并且假设系统内的较小温度变化不会改变热容比γ。密闭腔室（空气的俘获体积）中的压力P和体积V的绝热定律表示为：

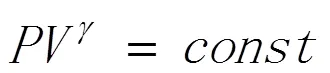
在使用该模型的仿真中，将初始状态选择为参考状态，以便在任何时候对于缓冲体积Vc的缓冲表压Pc的状态方程为：

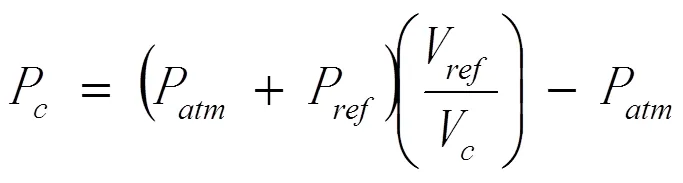
参考压力通常基于支撑ACV重量所需的设计压力，尽管可以考虑其他静态或工作条件。

这种简单的绝热模型将垫子视为被空气被捕获的空气囊，不包括流过裙板和裙板下方的任何缝隙或来自提升风扇的气流。

在每个时间步长，该压力在与水面或地面相交时，会在ACV缓冲垫的瞬时表面上积分，以便确定施加的总力和力矩。然后，对ACV运动的各个动力学方程式进行求解，以确定模拟中每个前进步骤的新位置和缓冲体积。

该模型本身不包括阻力和裙边接触模型，其作用就像是一个简单的质量弹簧系统，除了由于水波辐射引起的阻尼之外，没有阻尼。给定起伏的初始扰动，载具的响应在缓冲体积的固有频率处显示出无阻尼的振动，如图6所示。由于附加的附加质量，自由表面上ACV的相同扰动具有不同的固有频率。以及水的静水恢复，并且由于能量被水波带走，还显示出一定程度的振动衰减。水的平均下沉是由于水在施加的垫层压力作用下的稳态位移所致。

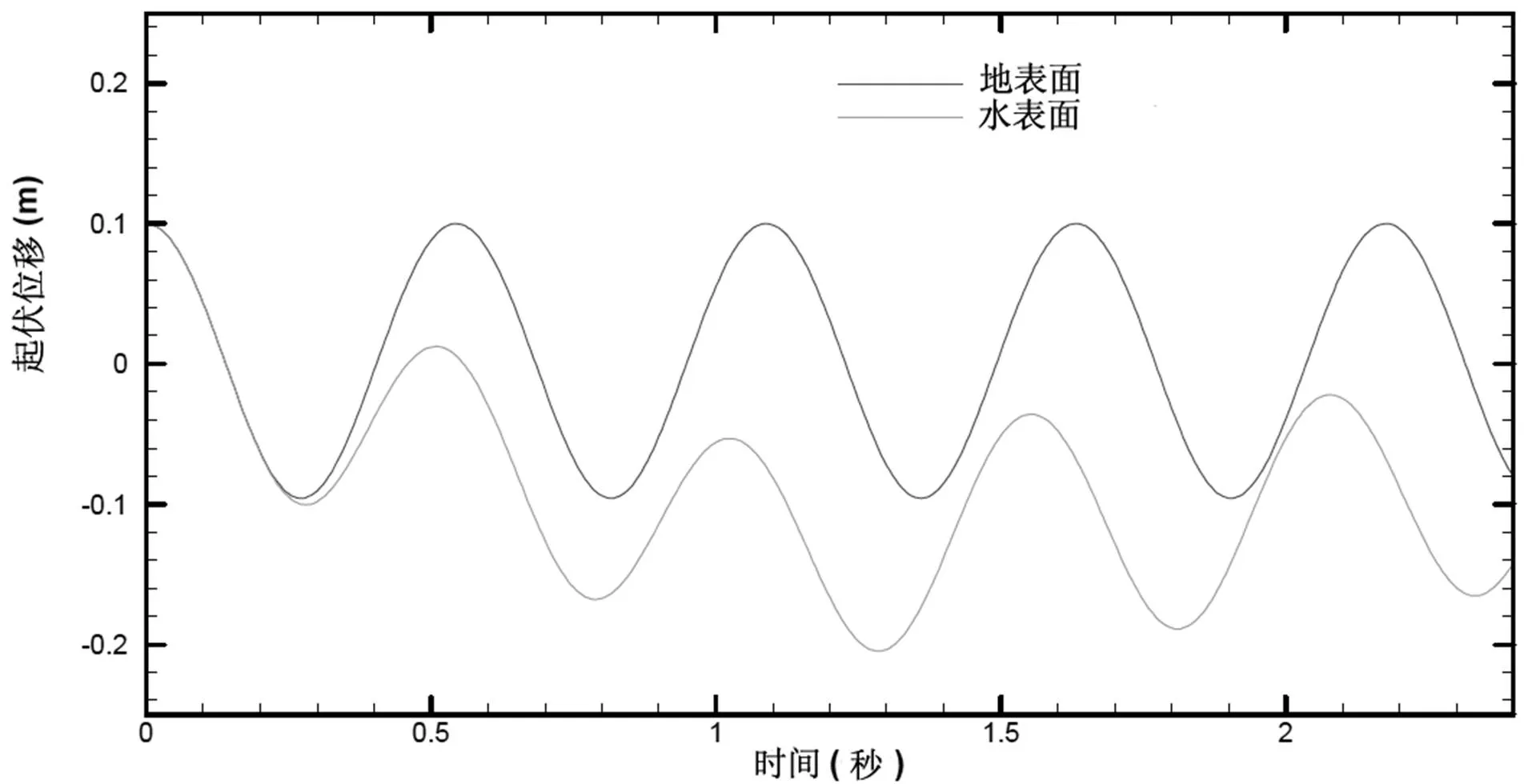
图6 使用俘获气泡模型在坚硬地面和无水表面上对全尺寸ACV初始位移的起伏响应。

3.2 流连续性模型

复杂的ACV气流系统的现实模型可能包括考虑起吊风扇，内部气囊腔和孔口流量以及裙部与地面或波浪表面之间以及通过裙部指部的出口流。

气流模型的准静态和动态版本已实现。在这两种情况下，ACV的每个腔室和缓冲垫内的压力密度关系的状态方程仍基于绝热假设。这样就可以为互连的风扇，气室，袋子和分段式气垫提供集总的参数公式。虽然绝热关系严格地是准静态的，但通过腔室之间的流动和提升风扇的特性，动态空气流动模型中包含了动态影响。

3.3 准静态模型

在纯准静态模型中，气流连续性平衡表示为：

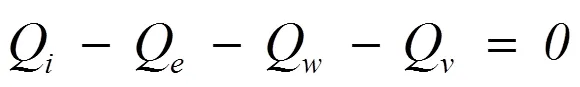
遵循在Yun和Bliault(2000)中发现的符号和公式。由升力风机供给到气垫的典型气流路径如图3所示。式7中的前两项分别表示流入和流出控制体积的流量，后两项表示由于载具和自由表面的相对运动而引起的控制体积容积的变化。

进口风机流量通过风机静态特性曲线与压头相关：

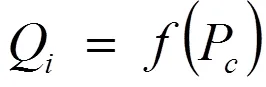
边缘间隙的流量基于边缘间隙的总面积Ae和孔口系数φ以及间隙上的表压：

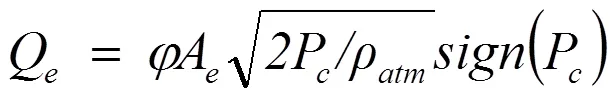
基于绝热关系，体积和压力的变化会产生通量：

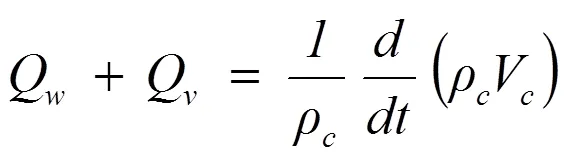
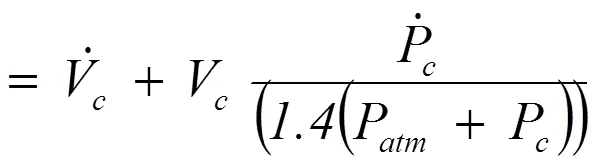
用牛顿-拉夫逊（Newton-Raphson）寻根法在每个时间步求解这个非线性方程，解析表达式定义了的每个分量。该方法已应用于单个ACV缓冲器和纵向分段缓冲器。

虽然在准静态公式中可以包含用于囊和提升风扇气室的单独腔室，但由于孔口阻力和不稳定的提升风扇特性在不稳定的模拟中很重要，因此这些扩展仅在动态模型中实现。

由于准静态方法在以前的研究中得到了广泛的应用，因此也包括了准静态方法。它提供了一个基准，可以与使用更先进的缓冲垫模型进行的仿真进行比较。

3.3 动态模型

为了包括与时间有关的节流孔阻尼和不稳定的提升风扇效应，采用了气流连续性方程的动态表示(Captain等，1978)。采用四阶龙格库塔（Fourth-order Runge Kutta）积分法求解稳定的数值解。这与ACV刚体运动分离方程的积分方法相同，使压力状态方程和体运动方程的局部精度具有可比性。

在集总参数方法中，每个腔室、升压风机静压室、袋段和单个或多个气垫分别平衡，并通过孔板流及其相关的压降及时明确地联系在一起。

气流连续性方程的动力学等效为：

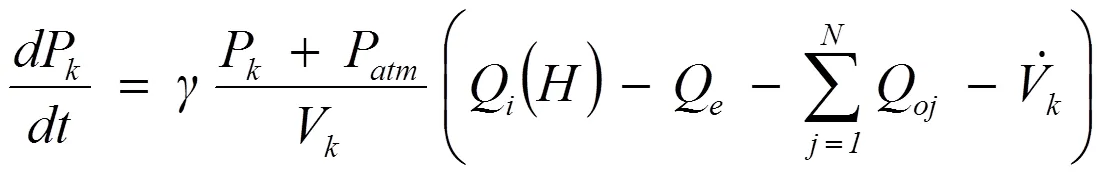
其中，Pk和Vk是每个腔室的表压和体积，Qi是作为压头函数的入口风扇流量，H，穿过入口风扇流量，Qe是上述的边缘间隙流量，Qo是每个相邻室的孔口的集合，如图中所示。例如，这将包括袋孔通过手指进入气垫的效果。这个压力方程的数值积分很敏感，因为它必须与运动方程具有相同的阶数和精度。此外，单独的体积导数也必须具有与压力积分相同的精度，以避免误差增加。

升力风扇的非稳态效应可以通过向气流添加惯性来使用动态方法进行建模。在气流连续性方程中加入一个辅助方程，形式如下：

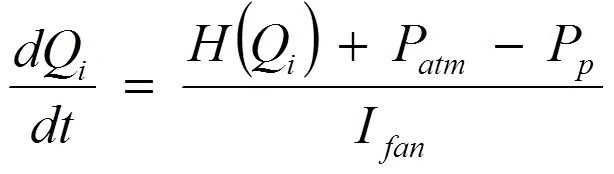
其中H是从静态特性曲线穿过风扇的静压上升，Pp是增压室中的压力，I是抵抗流量变化的惯性。

根据Captain等人进行的物理测试和分析(1975)，这种惯性的形式是风扇管道总几何形状的函数，并采用以下形式：

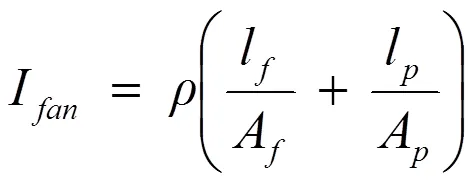
其中lf和lp是风扇和压力通风系统的长度，Af和Ap是它们各自的横截面积。

动态模型对不稳定气流建模的重要性如下图7所示。由于动态模型中增加的惯性和容积效应，谐振响应在幅度和频率方面的差异是明显的。由于这是一个弱非线性动力系统，因此对于相同的初始扰动，幅度有一定程度的不同。此外，所得平均值和裙边与地面之间的相关间隙也存在一些差异。

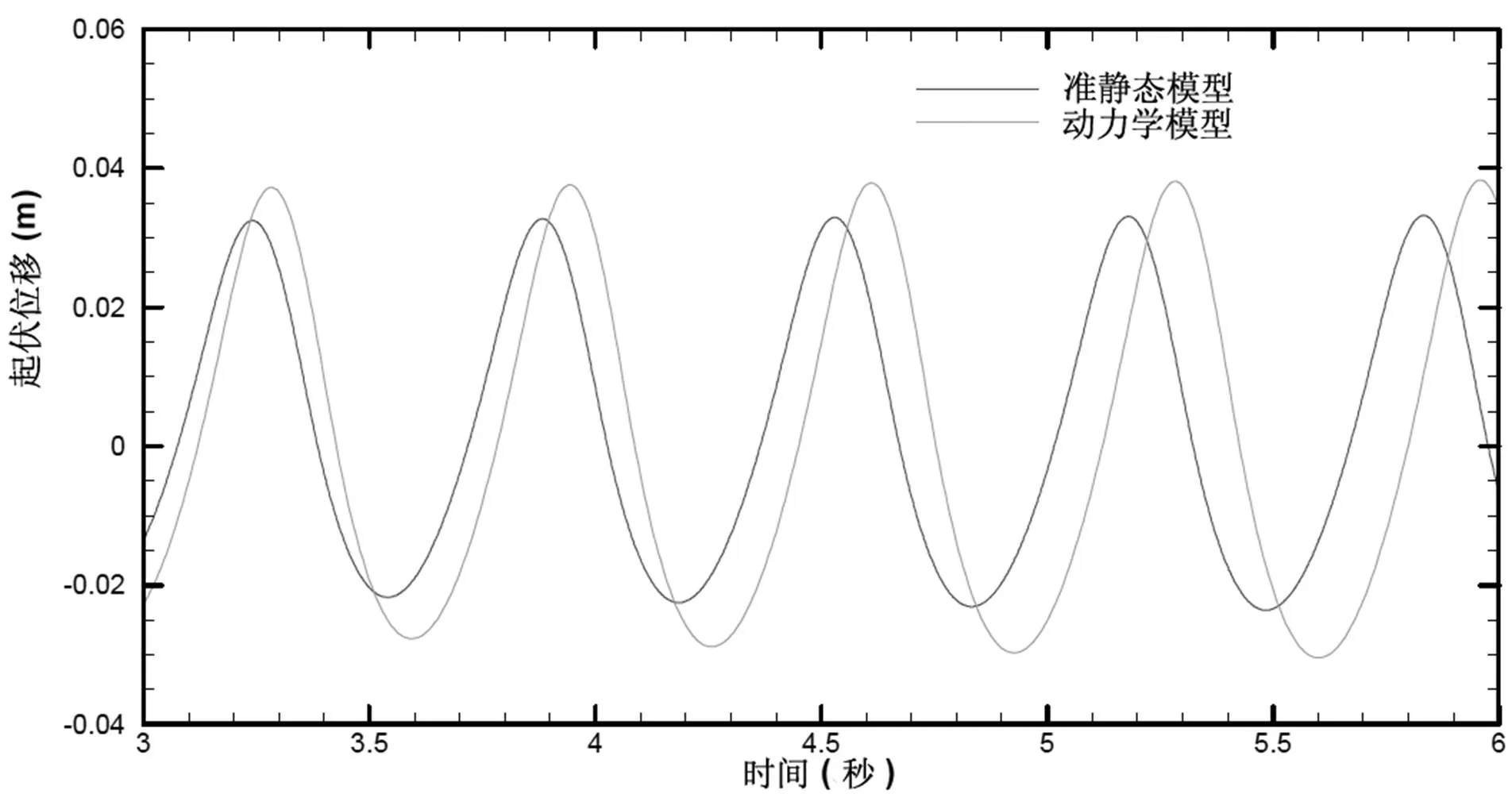
图7 硬表面上全尺寸ACV的准静态和动态模型之间的升沉响应比较

3.4 三维波方程模型

三维波动方程模型消除了气垫内部压力均匀性的假设，提供了捕获横摇-俯仰耦合的能力，在风浪的海洋中进行模拟，并有可能解决高阶气垫模式的共振行为。我们的实施方案(米利wski等人，2007)代表了表面效应船(Sorensen和Egeland, 1995)一维波动方程气垫模型的重要扩展，该模型使用模拟态解来获取气垫中的纵向压力变化，并且只适用于迎浪和具有大长梁比的结构。

通过求解三维波动方程，对密度为ρc和声速为c的缓冲空气进行动力学模拟。

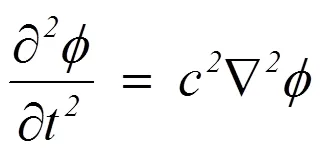
边界条件由边界速度的法向分量给出

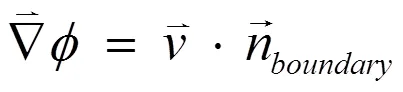
然后通过以下方式找到垫子中任何给定时间的压力

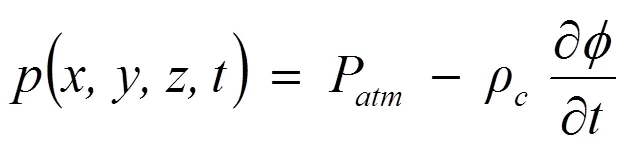
然后通过对边界上的压力进行积分来计算对载具、裙部和自由表面的力。

（未完待续）