APPROXIMATIONS OF THE IDENTITY ADAPTED TO CONTINUOUS ELLIPSOID COVER
2021-11-24YUAnkangLIBaode
YU An-kang,LI Bao-de
(School of Mathematics and System Sciences,Xinjiang University,Urumqi 830046,China)
Abstract:In this paper we develop some approximation of the identity results adapted to continuous multi-level ellipsoid cover.By using real-variable methods of harmonic analysis,we obtain two approximations of the identity results uniformly in some compact subset of Rnand in L1(Rn)norm,respectively.These results generalize the corresponding classical and anisotropic approximation of the identity results.
Keywords: approximation of the identity;ellipsoid cover;anisotropy
1 Introduction
As we all know,approximation of identity plays an important role in analysis,see[1-3].There are numerous approximations of identity results associated with the Euclidian balls in Rn.For example,let φ be an integrable function on Rnsuch thatRRnφ(x)dx=1,and for t>0 define φt(x)=t−nφ(t−1x).Then,if f ∈ L1(Rn),φt∗ f → f(t→ 0)in L1(Rn).
In 2010,the continuous multi-level ellipsoid cover Θ introduced by Dahmen,Dekel and Petrushev[4]consist of ellipsoids θx,t=Mx,t(Bn)+x,where Mx,tis an invertible matrix and Bnis the unit ball in Rn(see Definition 2.1).The flexible framework of continuous ellipsoid cover Θ introduced in this paper may have the ability to solve the following problems.For example,the formation of shocks results in jump discontinuities of solutions of hyperbolic conservation laws across lower dimensional manifolds.The case such jumps cause a serious obstruction to appropriate regularity theorems,since the available regularity scales are either inherently isotropic or coordinate biased or are subject to an uncontrollable restricted regularity range.For more development of continuous ellipsoid cover,see[5-7].
Inspired by the above work,for any θx,t=Mx,t(Rn)+x ∈ Θ,let φ be an integrable function on Rnsuch thatRRnφdx=1,we can define

And then a question arises:Is it possible to obtain some approximations of the identity results adapted to ellipsoid cover Θ such as f∗φx,t(x)→ f(x)(t→ ∞)in various senses?This article gives some affirmative answers for the question.It is worth pointing out that the approximation of the identity in this paper is done in Cc(Rn),which is a dense subset of L1(Rn),and the approximation of the identity in L1(Rn)is difficult for us,which is still open at the moment.
The organization of this article is as follows.In Section 2,we first present some notation and notions used in this article including continuous ellipsoid cover Θ and describe our main theorem.In Section 3,we show the proof details of the main theorem.
2 Preliminaries and Main Results
In this section we recall the properties of ellipsoid cover which was originally introduced by Dahmen,Dekel,and Petruschev[4].An ellipsoid ξ in Rnis an image of the Euclidean unit ball Bn:={x∈Rn:|x|<1}under an affine transform,i.e.,



3 Proof of Theorem 2.4
Proof(i)By f∈Cc(Rn),we know that there exists a positive constant N and M such that suppf⊂NBnand|f(x)|≤M for any x∈Rn,and f is a uniformly continuous function on Rn.By this,we obtain that,for any ε>0,there exists δ>0 such that,for all x∈Rn,y∈Rnwith|y|<δ,
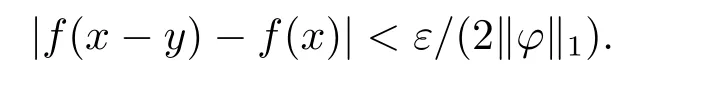


杂志排行
数学杂志的其它文章
- 分数阶拉普拉斯方程的一种新型有限差分方法
- 一类非线性随机微分方程的统计性质
- 阿贝尔方程的两个周期解的存在性
- AN OPTIMAL DIVIDEND STRATEGY IN THE DISCRETE MODEL WHEN PAYMENTS ARE SUBJECT TO BOTH TRANSACTION COSTS AND TAXES
- DIFFERENTIAL MIXED EQUILIBRIUM PROBLEMS IN BANACH SPACE
- THE REPRESENTATION CATEGORIES OF DIAGONAL CROSSED PRODUCTS OF INFINITE-DIMENSIONAL COFROBENIUS HOPF ALGEBRAS
