基于有限元法对宽板弯曲中性层内移规律的探讨*
2021-11-24胡一博刘能锋
胡一博,刘能锋
(哈尔滨工业大学(深圳)实验与创新实践教育中心,广东 深圳 518000)
折弯工艺作为板类零件最基础的加工工艺之一,在工业上有着极为广泛的应用。在板材弯曲过程中,外层受到拉应力作用,产生拉伸应变;内层受到压应力作用,产生压缩应变。在其断面上必然会有一层拉伸应变量与压缩应变量相等,该层叫作弯曲中性层[1]。国内外学者一直以来对板材弯曲现象进行了诸多的研究,经过长期的实验证明,板材在弯曲的过程中,弯曲中性层会出现向内偏移的现象。但是工业上对中性层内移程度往往依赖于经验数据,具有一定的局限性。本文通过数值分析[2]的相关方法,以有限元实验的实验数据作为基础,探究宽板在折弯过程中中性层内移程度的变化规律。
1 研究方法
1.1 有限元法
有限元法是将连续的宏观的求解域离散成许多微小的单元集合,根据各个微小单元与微小单元的相对关系和边界条件,求解出各个单元的未知变量,最后将每个微小单元的数据进行整合,将计算结果反馈到宏观问题,得到宏观问题的解的一种研究方法。这种求解方法随着计算机技术得到发展,越来越多地得到普及。大量实验证明,有限元法求解的结果较为可靠[3]。有限元法相比起实物实验,有着较多的优点,特别是针对实物实验中难以观测的数据,比如应力、应变、载荷和摩擦条件等数据,都可以通过有限元实验进行精准的设定与测量,为后期数据采集与分析工作带来极大的便利。有限元分析中最常用的通用有限元软件有Ansys、Abaqus 等,它们虽然适用性广、兼容性高,但是这些软件在前处理的设置(如约束,加载,接触,摩擦条件等)过程中过于繁琐[4],在对塑性成形过程仿真的使用上有诸多不便。本次实验选用专门针对塑性成形工艺开发设计的Deform 有限元软件进行实验。
1.2 宽板折弯有限元仿真模型
宽板折弯问题一直以来有诸多的研究,宽板折弯的时候,工件宽度方向上的尺寸远远大于厚度方向上的尺寸,所以学者们普遍认为,宽板折弯过程中工件宽度方向的变形量甚微,宽度方向可以近似看作为无变形。宽板折弯的有限元仿真模型可以从三维模型简化为平面模型进行求解与计算[5],极大地降低了建模难度、提高了计算效率。本次实验中,采用平面模型作为研究模型,追踪宽板折弯过程中中性层内移程度的变化规律。Deform 软件中有单独为研究平面塑性问题开发的有限元仿真模块Deform-2D,利用该模块下的建模工具,建立宽板折弯的平面模型如图1 所示。

图1 Deform-2D 中的二维模型
2 宽板折弯有限元仿真
2.1 材料选择
在研究宽板弯曲过程中结合中性层内移程度变化规律,为了使本次实验结果更接近实际情况,在材料选择上选取工业上较为常见的10 号冷轧钢板作为实验材料。10 号钢塑性、韧性很好,是冷加工工艺里最常用的材料之一[6],经常用作冷轧、冷冲、冷弯等工艺成形。工业上对10 号钢力学指标有准确的测定,采用已有的力学指标进行计算分析能够降低数据处理难度。部分力学参数如表1 所示。

表1 10 号钢的部分力学参数
2.2 应力应变模型
在常温下,10 号钢进行宽板折弯工艺过程中,不存在剧烈变形行为,无需考虑微观变形机制,只需考虑宏观参数对流动应力和应变的影响,所以流动应力-应变模型为其中为流动应力、为等效应变、T 为变形温度。本次实验过程中,变形温度T 保持不变。Deform 软件的材料库里有10 号钢的力学参数和流动应力应变关系,本次实验所用的流动应力-应变关系曲线如图2 所示。

图2 10 号钢流动应力-应变曲线
2.3 工艺参数设定
在实验模型已定的情况下,折弯工艺相关的实验参数有模具下压速度、凸模圆角半径、凹模圆角半径、摩擦因子和环境温度等。为确保结果的可靠性,参数选取上以更贴近实际情况为准,具体参数设置如表2 所示。模具与被折弯板材间的摩擦边界条件按照常剪切因子摩擦模型施加,尽量减小因为参数选择不当而造成的误差。

表2 工艺参数设定
2.4 有限元网格划分
进行有限元实验之前,需要对分析对象进行网格划分。本次实验将对被折弯板材进行网格划分,在Deform 软件中,网格的类型有两种:一种是三角形网格,三角形网格的分布杂乱无章,很难通过三个节点的“点”信息追踪中性层变化的“线”信息。另外一种是四边形网格,四边形网格呈矩形规则排列,如图3 所示。把宽板划分的四边形网格进行分层,由内层到外层依次为第1 层到第15 层。根据四边形网格四个节点的“点”信息,可以实时追踪各个层的长度变化,从而追踪中性层向内偏移的程度。

图3 宽板网格划分示意图
通常使用中性层内移系数λ 来描述中性层内移程度的大小。应变中性层内移系数λ 是中性层与最内层距离T 与板厚t 的比值,即λ=T/t,其中T 为中性层与最内层距离,t 为板材厚度。由此可知,应变中性层内移系数λ 值越小,应变中性层内移程度越大。我们选取板材中部60mm 长度的节点群作为研究对象,在板材弯曲变形时候,记录各个四边形网格四个节点处的应变数据,追踪各层的长度变化。图4 是在不同步数下,部分节点坐标示意图。就第1 层(最外层)而言,在第1 步的时候(弯曲变形尚未开始),第1 层的长度可以表示为该层上所有相邻两个节点距离之和。在第300 步的时候,由于网格划分的足够小,所以第1 层的长度可以近似的表示为该层上所有相邻两个节点距离之和,即:

图4 不同步数下的节点坐标

其中,(xn,yn)代表该层上的编号为n 的节点坐标。所以只要有每一层上所有的节点坐标数据,我们就可以计算出该层的长度L,从而追踪中性层的内移程度。
2.5 其他参数设定
为了使有限元实验结果更加趋近于实际情况,根据文献资料分析整合并对模拟参数进行详细调整,力求达到较为精确的数值模拟结果。
(1)板材厚度取2mm。
(2)选用不同的摩擦系数(0.04、0.08、0.12)来对结果进行分析。
(3)选择Newton-Raphson 式的迭代计算方法。
(4)毛坯类型设置为塑性体,且考虑后期的加工硬化现象。模具类型设置为刚体。
(5)凸模采用等速给进的方式,给进速度设置为1mm/s。
(6)在恒温下进行有限元实验,环境温度设置为20℃,实验中仅使用应力应变模块,不使用热传导模块。
(7)给进的步数根据弯曲程度而定,细化弯曲成形末期的步数,以便更准确地分析结果。
(8)储存间隔步数设置为1 步。
3 实验数据分析
3.1 实验结果
宽板弯曲有限元实验结束后实验结果如图5 所示,被折弯件已发生塑性变形,折弯效果良好。本次实验共记录了562 步的节点数据,每一步均有所有节点的应变数据供分析使用。

图5 折弯末期应变示意图
3.2 中性层内移系数与相对弯曲半径的关系
在折弯工艺中,常常用相对弯曲半径来描述板材的折弯程度,相对弯曲半径r/t 是折弯区的圆角半径r与板厚t 的比值。由此可知,相对弯曲半径r/t 越大,板材弯曲程度越小;相对弯曲半径r/t 越小,板材弯曲程度越大。
在折弯初期,折弯应变量较小,所以每一步凸模下压量较大。折弯中期,折弯区域有较为明显的应变,所以将第99 步后的单步凸模下压量进行细化,每一步下压量有所减小,读取每一步下的节点应变数据,将每一步的节点数据进行处理,得到中性层内移系数λ 与相对弯曲半径r/t 的数据。表3 是初始板厚为2mm 时,不同步数下,相对弯曲半径与中性层内移系数的数据,由于数据总量较多,该表仅列出部分数据。

表3 内移系数与相对弯曲半径变化数据
根据表3 数据可绘制出图6 所示的曲线,其中横坐标为相对弯曲半径,纵坐标对应的是中性层内移系数。由图可以看出,折弯初期,相对弯曲半径r/t>8 的时候,中性层位置基本不发生移动。随着折弯过程的进行,相对弯曲半径r/t<8 的时候,中性层位置发生了明显的内移,内移系数也开始发生明显的变化。折弯程度越大,内移系数越小,中性层内移程度越大。

图6 内移系数与相对弯曲半径的关系
3.3 数值分析
为了能够更好地描述内移系数与相对弯曲半径之间的关系,往往需要寻求一个数值模型来描述两个变量的数学关系。由内移系数与相对弯曲半径关系曲线观察可知,该曲线前半段斜率较小,后半段斜率较大。因此,尝试采用指数模型:λ=aebx+cedx对该曲线进行拟合,其中,λ 表示中性层内移系数,x 表示相对弯曲半径。用拟合工具进行拟合处理后,拟合结果如下:

内移系数与相对弯曲半径的拟合曲线误差平方和(SSE)为1.127×10-4,复相关系数(R-square)为0.9986,说明该拟合结果可信度高。原始数据与拟合结果的对比如图7 所示。
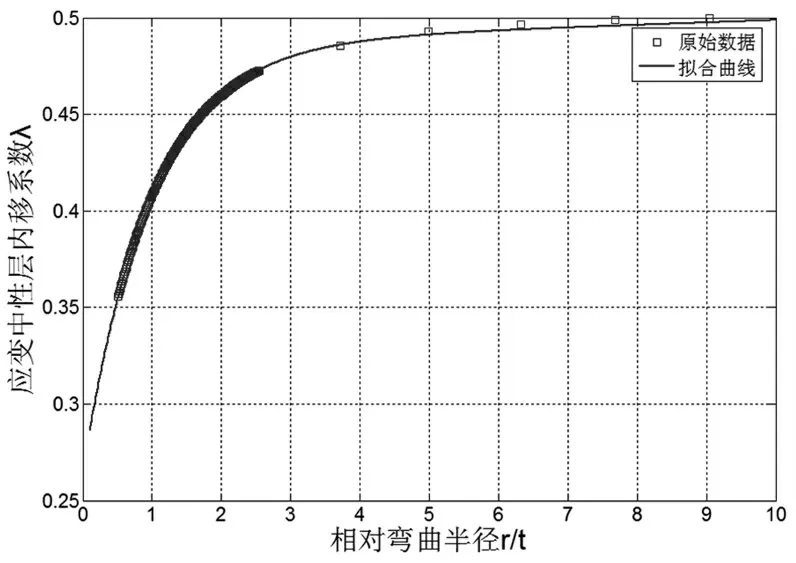
图7 拟合曲线与原始数据对比图
摩擦力的存在影响着金属的流动,所以摩擦力也会对中性层的位置产生一些影响,探讨摩擦力对内移系数λ 的影响,在不改变其他参数的情况下,仅仅改变摩擦系数μ,分别做两组对比实验,来探讨不同的摩擦系数μ 对内移系数λ 的影响。拟合结果如表4 所示。

表4 不同摩擦系数μ 下变薄内移系数的拟合结果
图8 是不同摩擦因子下,模拟结果的对比图。从图中可以看出,在弯曲前期(相对弯曲半径r/t>8),不同摩擦系数μ 下的内移系数λ 均接近于0.5,说明从弯曲开始到相对弯曲半径r/t=8 时,在不同摩擦系数μ下,应变中性层内移程度很小,基本不发生内移。在弯曲中期(相对弯曲半径4 图8 不同摩擦系数μ 下变薄系数的拟合曲线对比图 (1)中性层内移系数与相对弯曲半径关系的曲线呈现为幂指数的变化关系,即λ=aebx+cedx。其中λ 是中性层内移系数,x 是相对弯曲半径。a、b、c、d 为待定系数,取值与弯曲工艺参数有关。 (2)从有限元实验来看,板材在折弯程度相同的情况下,随着板材与模具的摩擦力越大,中性层内移程度也越大。
4 结论
