关于魏尔斯特拉斯在数学分析中的两个重要贡献
2021-11-24高义
高 义
(北方民族大学数学与信息科学学院,宁夏银川 750021)
0 引言
魏尔斯特拉斯(Weierstrass,1815-1897)是世界上著名的领军数学家之一,由于在柯西(Cauchy,1789-1857)、阿贝尔(Abel,1802—1829)等开创的数学分析的严格化潮流中,以ε-δ语言系统建立了实分析和复分析的基础,被誉为“现代分析之父”[1].他在幂级数理论、实分析、复变函数、阿贝尔函数、无穷乘积、变分学、双线型与二次型、整函数、椭圆函数论等诸多领域中做出了伟大的贡献.在大学《数学分析》教材中,魏尔斯特拉斯的名字多次出现,令人印象深刻,如魏尔斯特拉斯致密性定理,即有界数列必有收敛子列;关于函数一致收敛的魏尔斯特拉斯判别方法;闭区间上连续函数的最值定理;处处连续但处处不可导函数的例子;魏尔斯特拉斯第一和第二逼近定理等.魏尔斯特拉斯值得世人无比敬仰的另一个原因是他的锲而不舍的精神,他40岁之前无人知晓,从大学毕业就在乡村中学教书,只是一个默默无闻的中学老师,尽管教学任务多么繁重,条件多么艰苦,他从没有放弃对数学的研究,其数学成果终于在他40岁之后获得世人的瞩目[2].魏尔斯特拉斯不仅在数学研究上做出了影响深远的工作,而且在教学上也成绩斐然,并培养了大批的著名数学家,如耳熟能详的柯瓦列夫斯卡娅(Kovalevskaya,1850-1891)、闵可夫斯基(Minkowski,1864-1909)、斯托尔茨(Stolz,1842-1905)、施瓦茨(Schwarz,1843-1921)、赫尔德(Hölder,1859-1937)、米塔-列夫勒(Mittag-Leffler,1846-1927)等[1-3].
魏尔斯特拉斯构造的处处连续处处不可导的函数[3,4]无疑颠覆了人们对函数的认识观,直到现在对于很多不从事大学数学教学和研究的人也感到不可思议.魏尔斯特拉斯第一和第二逼近定理[5,6]更是奠定了逼近论的基础,其意义超越了连续函数可以由多项式函数逼近的这一重要发现的本身,使人们进一步认识到可以通过简单的可计算函数逼近或表征复杂的函数.然而,对于这两个非常重要的工作,由于证明稍有难度和教材篇幅的限制,国内鲜有教材在大学本科阶段对其进行详尽的介绍和证明.若不稍加引导的话,学生对这两个工作往往不能够引起足够的重视.事实上,这两个工作对于具有一定数学分析基础的同学是不难理解的.本文主要介绍魏尔斯特拉斯在数学分析中的这两个重要工作.首先,对魏尔斯特拉斯构造的第一个处处连续处处不可导的函数给出了文献[4]中的证明方法;其次介绍魏尔斯特拉斯第一和第二逼近定理,给出魏尔斯特拉斯第二逼近定理的一种构造性证明方法,进而借助文献[6]的方法阐明了魏尔斯特拉斯第一和第二逼近定理的等价关系.论文对了解魏尔斯特拉斯在分析学上的贡献有一定借鉴意义,同时对逼近论初学者有一定参考价值.
1 处处连续处处不可导的函数
在微积分诞生初期乃至诞生后的两个世纪里,人们曾直观地认为连续函数在其定义域中不可导的点至多是可数集,很难想象处处连续处处不可导函数的存在性.然而,直到1872年,魏尔斯特拉斯构造出了一个处处连续处处不可导的函数,才彻底改变了人们对连续函数的认识,引起了数学界的极大震动[3,4].此后,大量的处处连续处处不可导的函数被构造出来,称之为魏尔斯特拉斯函数.进一步,人们从集合的观点分析,魏尔斯特拉斯函数所构成的集合是第二纲集[7-9],这意味着这样的函数不仅存在而且有很多,远远多于我们常见的初等函数,对这些函数的性质特别是几何意义的研究也直接推动了分形几何的创立[10-12].另外,魏尔斯特拉斯函数也广泛应用于随机过程的研究,如对布朗运动轨迹的刻画.本节主要介绍历史上第一个被发表的魏尔斯特拉斯函数,并给出文献[4]中对该函数处处连续处处不可导的证明方法.
1.1 魏尔斯特拉斯函数
1872年,魏尔斯特拉斯构造出如下的函数[3,4,7,13]:
(1)
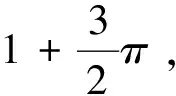
1.2 魏尔斯特拉斯函数性质的证明
定理1.1函数(1.1)在实轴上处处连续处处不可导.
证明:这里的证明主要基于文献[4]的方法.由于
|bncosanπx|≤bn
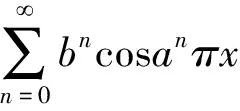
固定x∈(-∞,+∞),对每个正整数m,令αm是一个最接近amx的整数,并且令
xm=amx-αm
(2)
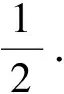
(3)

(4)
因此,有
ym 考虑 (5) 首先估计第一项I,对于n=0,1,…,m-1,利用微分中值定理,得 (6) 其次,估计第二项J.因为a是一个正奇整数,αm是一个整数,则有 cos(an+mymπ)=cos(anπ(αm-1))=(-1)αm-1 (7) (-1)αmcos(amxπ)+1=(-1)αmcos((xm+αm)π)+1=cos(xmπ)+1≥1. 这样, (8) 因此 (9) 即 |I|<|J| (10) 结合式(6)和(9),则有 其中β>0.因此 由x∈(-∞,+∞)的任意性,知f(x)在(-∞,+∞)处处不可导. 注1.1 最新的文献[14]给出了上面类似的证明. 注1.2 文献[3,15-17]讨论的是关于荷兰数学家Van der Waerden于1930年给出的处处连续处处不可导函数的例子的证明,该函数写为: (11) 设C[a,b]表示闭区间[a,b]上连续函数全体,C2π表示以2π为周期的连续函数全体.1885年,魏尔斯特拉斯首先指出用多项式逼近连续函数是可能的,后人称之为Weierstrass逼近定理. 定理2.1[6]若f(x)∈C[a,b],则对于任意给定的正数ε,都存在代数多项式p(x),使得对于一切x∈[a,b],满足不等式 |f(x)-p(x)|<ε (12) 定理2.2[6]若f(x)∈C2π,则对于任意给定的正数ε,都存在三角多项式t(x),使得对于一切x∈(-∞,+∞),满足不等式 |f(x)-t(x)|<ε (13) 定理2.1被称为魏尔斯特拉斯第一逼近定理,定理2.2被称为魏尔斯特拉斯第二逼近定理,这两个定理在数学分析中具有非常重要的地位,著名逼近论专家A.F.Timan对魏尔斯特拉斯逼近定理曾这样评价[4]: The basis of the theory of approximation of functions of a real variable is a theorem discovered by Weierstrass which is of great importance in the development of the whole of mathematical analysis. 关于定理2.1和定理2.2的证明有很多文献专门讨论过,一般利用分析法和构造法去证明,经典的构造法如借助伯恩斯坦(Bernstein)多项式证明定理2.1,借助费耶(Fejér)和证明定理2.2,我们将结果写作如下. 定义2.1[5]若f(x)∈C[0,1],称多项式 (14) 为f(x)的n次Bernstein多项式或Bernstein算子. 定理2.3[5]若f(x)∈C[0,1],则Bernstein算子Bn(f;x)在[0,1]上一致收敛于f(x). 关于定理2.2的证明,有如下的构造方法. 定义2.2[19]若f(x)∈C2π,称积分 (15) 为Fejér和或Fejér算子. 定理2.4[19]若f(x)∈C2π,则Fejér算子σn(f;x)在全实轴上一致收敛于f(x). 本节主要在已有文献的基础上,借助瓦勒·布然(Vallée Poussin)算子对定理2.2给出另一种构造性证明.同时,讨论了定理2.1和定理2.2之间的等价性. 首先,我们引进Vallée Poussin算子. 定义2.3[5,6]若f(x)∈C2π,称积分 (16) 为Vallée Poussin算子. 显然,该算子为C2π到其自身的正线性算子,关于正线性算子的定义参见文献[6].利用变量代换,算子Vn(f;x)亦可写为: (17) 注意到 (18) 则不难得到关于Vn(f;x)的如下性质. 引理2.1 设Vn(f;x)为Vallée Poussin算子,则 (1)Vn(1;x)=1; (19) (20) (21) 为证明定理2.2,还需要引进柯罗夫金(Korovkin)定理. 定理2.5[20]设Ln(f;x)是C2π上的正线性算子序列,下列三条件满足: Ln(1;x)=1+αn(x),Ln(cost;x)=cosx+βn(x),Ln(sint;x)=sinx+γn(x), 其中αn(x),βn(x),γn(x)在全实轴上一致收敛于零,那么对于任一f(x)∈C2π,Ln(f;x)在全实轴上也一致收敛于f(x). 定理2.6 若f(x)∈C2π,则Vallée Poussin算子Vn(f;x)在全实轴上一致收敛于f(x). 证明:由引理2.1知,Vn(1;x),Vn(cost;x),Vn(sint;x)在全实轴上分别一致收敛于1,cosx,sinx,于是由Korovkin定理知Vn(f;x)在全实轴上也一致收敛于f(x). 注2.1Vallée Poussin算子可以充当定理2.2所要求的三角多项式. 一个自然的问题是,定理2.1和定理2.2有什么本质的联系?事实上,二者是等价的,等价性的证明参见文献[5,6]. 定理2.7 魏尔斯特拉斯第一和第二逼近定理是等价的. 证明:这里的证明主要基于文献[6]的方法.首先说明由定理2.1可以推出定理2.2.设f(x)∈C2π是个偶函数,则g(t)=f(arccost)是[-1,1]上的连续函数,此处arccost取主值.对任意给定的ε>0,由定理2.1,存在多项式p(t)满足 |g(t)-p(t)|<ε,t∈[-1,1] 于是 |f(x)-p(cosx)|<ε,x∈[0,π] 由于f(x)与p(cosx)都是周期为2π的偶函数,所以上式在整个实轴上成立,而且p(cosx)是一个三角多项式,这说明定理2.2对偶函数成立. 对于一般的情形,令 h1(x)=f(x)+f(-x),h2(x)=(f(x)-f(-x))sinx (22) 容易看出h1(x)与h2(x)都是周期为2π的偶函数.根据已经证明的部分,对任意给定的ε>0,有三角多项式t1(x)与t2(x),使得对于一切x∈(-∞,+∞),适合 |hi(x)-ti(x)|<ε,i=1,2 所以 |h1(x)sin2x-t1(x)sin2x|<ε (23) |h2(x)sinx-t2(x)sinx|<ε (24) 于是,有 |2f(x)sin2x-t3(x)|<2ε (25) (26) 因为上式是在全实轴上成立,所以 (27) 结合式(25)和(27),有 (28) |f(x)-t(x)|<ε 成立. 其次,证明由定理2.2可以推出定理2.1.设f∈C[-1,1],则f(cost)是周期为2π的连续函数,由定理2.2,存在三角多项式T(x)使得 |f(cost)-T(t)|<ε, -∞ 以-t代换变量t,有 |f(cost)-T(-t)|<ε 于是有 (29) 于是 (30) 即有 (31) 最后,说明在一般的闭区间[a,b]上定理2.1也成立.这里,只要利用一个变换即可: 这样,若f(t)∈C[-1,1],则f(x)∈C[a,b]. 本文主要讨论了魏尔斯特拉斯在数学分析中的两个伟大贡献,一个是关于处处连续但处处不可导函数的构造,另一个是魏尔斯特拉斯基本逼近定理.论文对逼近论初学者有一定参考价值.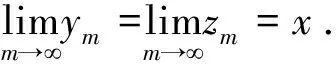
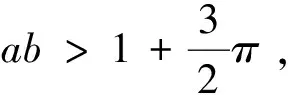
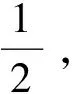
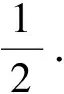
2 魏尔斯特拉斯第一和第二逼近定理
2.1 定理2.2的证明
2.2 定理2.1和定理2.2的等价性
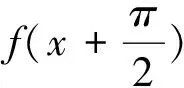
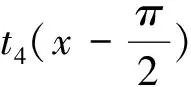
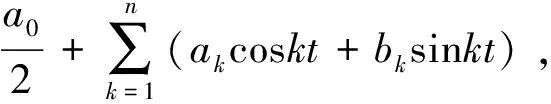
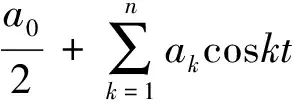
3 结论
