双层正交的光纤布拉格光栅柔性形状传感技术
2021-11-23郭永兴杨跃辉
郭永兴,杨跃辉,熊 丽
(1.武汉科技大学 冶金装备及其控制教育部重点实验室,湖北 武汉430081;2.武汉科技大学 机械传动与制造工程湖北省重点实验室,湖北 武汉430081)
1 引 言
软体机器人是近年来的研究热点。相比于传统采用电机驱动的刚性机器人,软体机器人采用具有良好柔韧性和适应性[1-2]的柔软材料制成,能在各种非结构化环境内改变自身的方向和形态[3-4]。因此,软体机器人技术在柔性仿生机器人、可穿戴柔性产品等领域体现出巨大的应用前景。与此同时,基于软体机器人柔性驱体自身的灵活和柔韧特性,在受到受外载荷、自身重力以及环境接触物的作用时它易发生不规则形变。因此,搭载形状传感器准确反馈柔性驱体的形状信息,是实现软体机器人精准控制的重要环节。
然而,传统的基于电磁原理的应变传感器[5-6],存在体积大、刚度大、零点温度漂移、弱电信号易受干扰及生物相容性差[7-8]等缺点,与软体机器人融合时难以满足柔性机器人的形状测量要求。光纤布拉格光栅(Fiber Bragg Grating,FBG)具备良好的柔韧性和弹性[9],加之易于植入集成[10-11]、耦合性好和串接稳定性高[12-13]等优势,使得FBG成为柔性机器人形状测量的首选传感元件。
基于FBG的独特优势,众多学者对FBG软体机器人形状测量技术进行了研究。Li等人[14]提出了一种基于平行双FBG阵列的不规则截面的柔性机械臂分布式曲率传感和形状重构方法。Wang等人[15]将FBG嵌入硅橡胶中,提出了一种基于FBG的形状传感算法和传感网络。Yi等人[16]介绍了一种正交曲率FBG传感器阵列,用于监测杆、龙骨等柔性结构的变形和振动。张润玺等人[17]提出一种针对仿章鱼软体机器人的形状控制算法。Wei等人[18]提出了一种新颖的单光纤螺旋结构加多FBG传感器来测量柔性机器人的形状。He等人[19]提出了一种嵌入式FBG的软手术执行器三维形状感知算法。当然,也有不少学者为测量物体表面曲率,对基于FBG的曲率传感器进行了研究。郑狄等人[20]设计了一种多芯FBG曲率传感器,并采用匹配滤波技术实现曲率解调。Zhang等人[21]将FBG嵌入硅橡胶中,提出了一种基于FBG的软曲率传感器。何彦霖等人[22]提岀并设计了基于聚氯乙烯(Polyvi⁃nyl Chloride,PVC)和硅胶复合基底的FBG柔性曲率传感器。Ge等人[23]将FBG偏心植入到凝胶中研制了一个双向曲率传感器。许西宁等人[24]利用光纤在不同弯曲曲率下的不同形变,提出并验证了一种基于七芯光纤和少模光纤的新型光纤曲率传感器。Sun等人[25]将FBG融入软硅-聚氯乙烯混合基底,提出了一种软曲率传感器。以上这些探索工作推动了软体机器人的发展,并为软体机器人的形状测量提供了参考。但是,大多数基于FBG的软体机器人形状传感器研究均是沿着纤维方向的线状形状重建,只能实现多点曲线形状传感,不能实现多点曲面形状传感。其次,大多数报道只实现了单方向纯弯曲形状测量,并没有实现复杂曲面的形状测量。此外,相关研究多数采用PVC、聚酰亚胺等刚性材料作为应变传感基体,并没有完全以柔性材料作为应变传感基体。
为解决上述问题,本文选取聚二甲基硅氧烷为实验基体,植入FBG阵列,研究了基于双层正交FBG的可实现三维形状重建的柔性形状传感器,并开展了实验测试,传感器可有效测量三维形状。
2 柔性形状传感器结构
FBG柔性传感器以聚二甲基硅氧烷(Polydimethylsiloxane,PDMS)作为衬底。PD⁃MS具备良好的光学性能和重复性,在清晰展现内部阵列FBG的同时,能在弹性变形内发生多次重复变形而不影响其力学性能。前期研究表明[26],过高的PDMS配比使得制作的软体基体硬度过高、脆性过大,测量时重复性低;过低的PD⁃MS配比使得制作的软体基体表面有黏稠感,不利于开展测试。因此,本文选取了测量响应较好,固化剂和液态PDMS配比为1∶5(应变传递率为0.64)的PDMS作为承载FBG的基体,并将FBG植入软体基体中。
图1所示为FBG柔性形状传感器的三维模型。传感器的尺寸为80 mm(长)×80 mm(宽)×3 mm(厚)。其中,所选用的FBG带宽均为0.2 nm,反射率均为90%。此外,上层和下层均阵列植入4根光纤,相邻光纤之间的距离为20 mm,每根光纤上等间距设置有4个FBG,相邻FBG之间的距离均为20 mm。上层光纤纤芯距离柔性基体中性层的距离为1.125 mm,下层光纤纤芯距离柔性基体中性层的距离为0.625 mm。上、下层阵列植入的光纤编号以及FBG中心波长的初始值如表1所示。
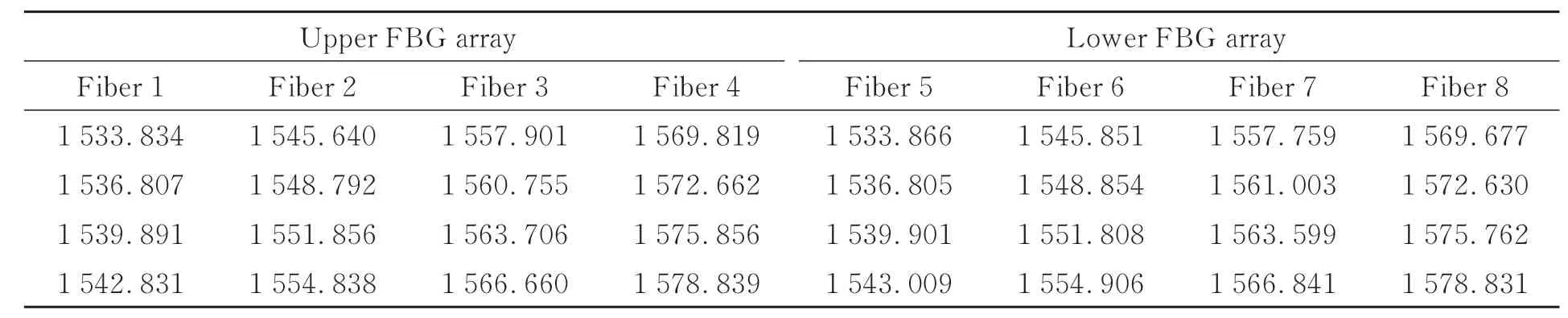
表1 上、下层阵列植入的光纤编号以及FBG中心波长初始值Tab.1 Numbers of fiber implanted in upper and lower arrays and initial value of FBG center wavelength (mm)
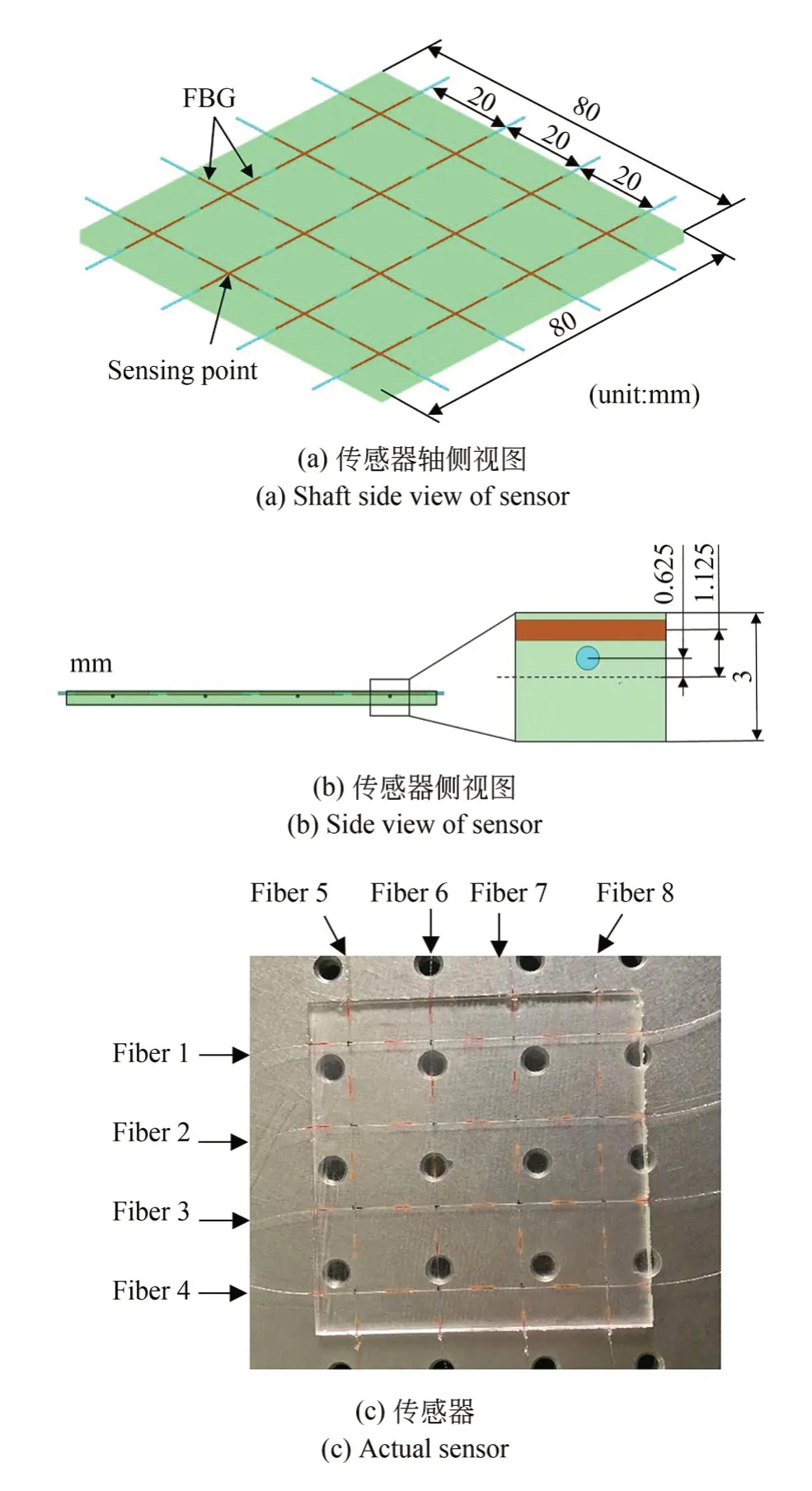
图1 基于光纤光栅的柔性机器人的形状传感器及其三维模型Fig.1 Shape sensor and 3D model of flexible robot based on FBG
3 测量原理
3.1 FBG的传感原理
图2为FBG结构和敏感原理示意图。FBG是由于光纤的光敏性产生折射率的改动,将光敏光纤暴露在紫外光束互相干涉带来的光波条纹里,形成折射率调制分布。根据光纤光栅的耦合模理论,FBG的光栅方程为:
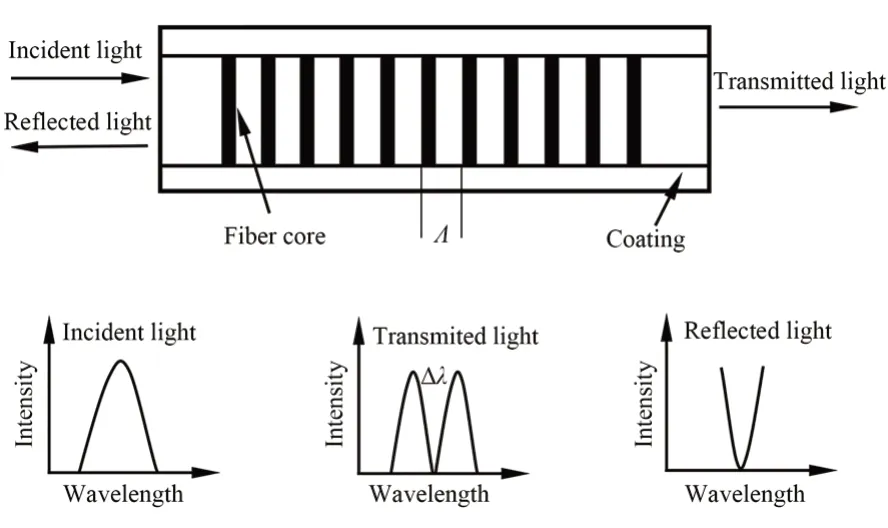
图2 光纤光栅结构及其敏感原理示意图Fig.2 Schematic diagram of structure and sensing princi⁃ple for FBG

式中:λB为FBG的中心波长,neff为光纤的有效折射率,Λ为栅格周期。
轴向应变和温度是影响FBG波长漂移的最直接因素。因此,FBG波长变化量与温度和应变的关系可以表示为:
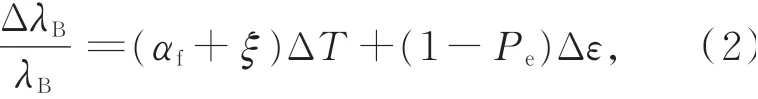
式中:λB为FBG的初始波长,ΔλB为波长变化量,αf为光纤的热膨胀系数,ξ为光纤材料的热光系数,Pe为光纤的弹光系数(常温时约等于0.22)。
3.2 变形曲率测量理论
曲率测量是基于柔性基体自身产生弯曲形变时基体内部的FBG被动地发生弯曲变形,引起FBG波长变化,从而得到弯曲应变。变形曲率测量原理是基于纯弯曲模型,每一个单独的FBG可视为一个曲率传感器。图3所示为FBG在传感器中的布置示意图。
当传感器处于自然状态时,如图3(a)所示,FBG受到的应变为0。当传感器处于弯曲状态时,如图3(b)所示,根据材料力学可知,中性层下方被拉伸,中性层上方被压缩,而中性层无应变。传感器处于自由状态时,中性层长度与FBG的有效测量长度相等,设传感器的中性层长度ab为L,传感器弯曲状态时FBG的有效长度为L cd,FBG距离中性层的距离bd为h,中性层的曲率半径ob为ρ,传感部位对应的圆心角为θc,可得:
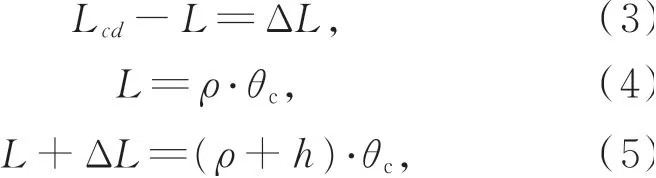
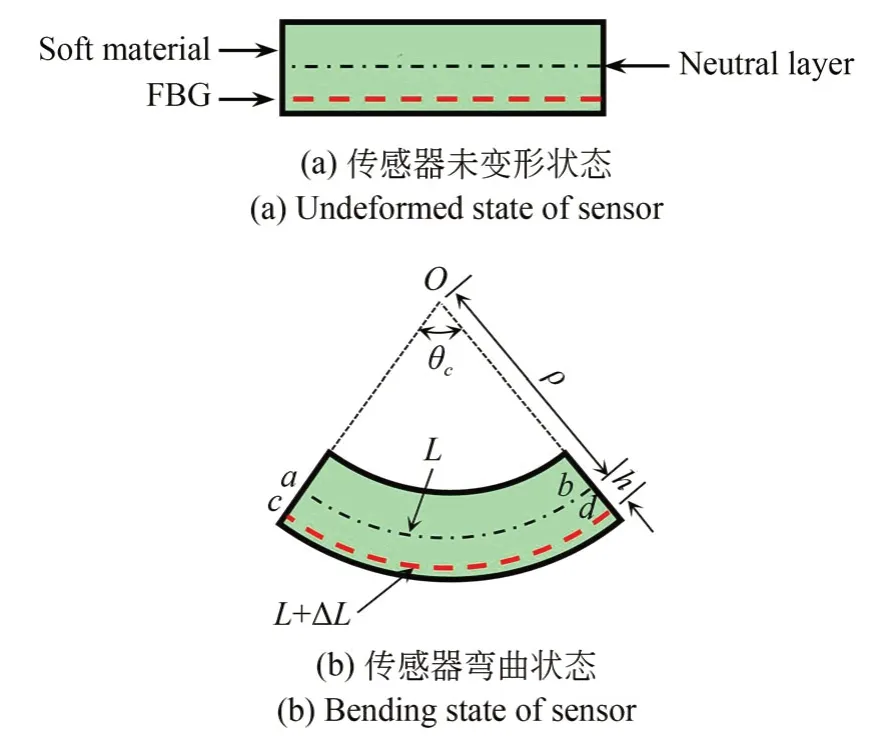
图3 传感器中FBG的布置示意图Fig.3 Schematic diagram of FBG arrangement in the sensor
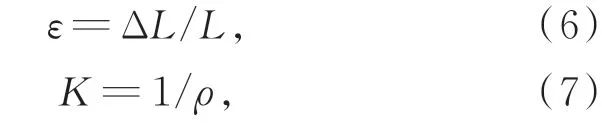
式中:ε为传感部位的轴向应变,K为曲率。由式(3)~式(7)可得:

在恒定温度条件下,结合式(2)和式(8)可得曲率K与FBG波长变化量ΔλB的关系式为:
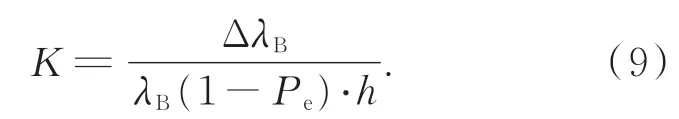
由式(9)可知,当FBG确定的情况下,λB,Pe以及h均为常数,曲率K与FBG波长变化量ΔλB呈线性关系。
3.3 三维形状重建理论
曲面重建原则为基于空间离散点的曲面重构。通过对波长漂移信息进行曲率反演,融合多个光栅测点的曲率信息,得到各个测量点的空间坐标,再用MATLAB对空间离散点的插值拟合来重建三维形状。
圆心角θ和弧长L的关系式为:
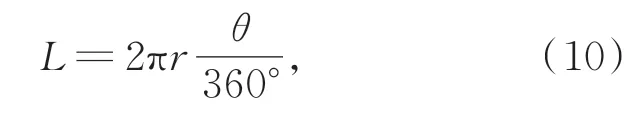
式中r为曲率半径,值为1/K。
将r=1/K代入式(10)可得圆心角θ与曲率K的关系式为:

以一根光纤为例来求解单根光纤上4个FBG传感点的空间坐标。为符合传感器中光纤多种弯曲形式,建立坐标系以及光纤模拟弯曲曲线如图4所示。图4中所有变量命名如表2所示。

表2 图4中所有变量命名Tab.2 Definition of all variables in Figure 4
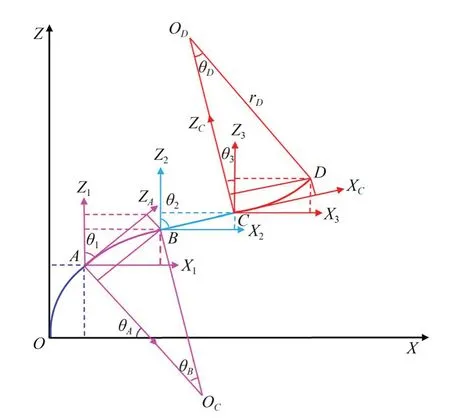
图4 光纤模拟弯曲曲线示意图Fig.4 Schematic diagram of optical fiber simulated bend⁃ing curve
假设每个FBG在长度范围内发生等曲率弯曲变化。当光纤发生弯曲变形时,可认为弧OA为FBG1测量长度;弧AB为FBG2测量长度;弧BC为FBG3测量长度;弧CD为FBG4测量长度。为 方 便 计 算,FBG1,FBG2,FBG3以 及FBG4的传感点分别定义为A,B,C和D,易知OA与AB,AB与BC,BC与CD均相切,所以曲率半径在该点均在同一直线上。根据数学函数关系分别求出A在坐标系XOZ中的坐标、B在坐标系X AAZA中的坐标、C在坐标系XBBZB中的坐标以及D在坐标系X CCZC中的坐标。再通过坐标系的平移和旋转,求出A,B,C,D在坐标系XOZ中的坐标。
经计算得A点坐标:
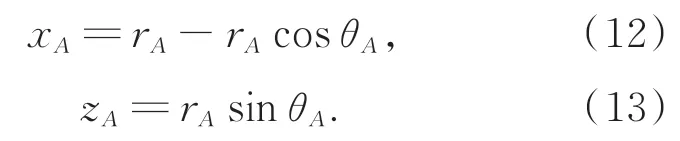
B点坐标:C点坐标:
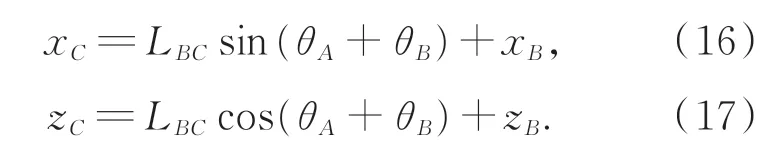
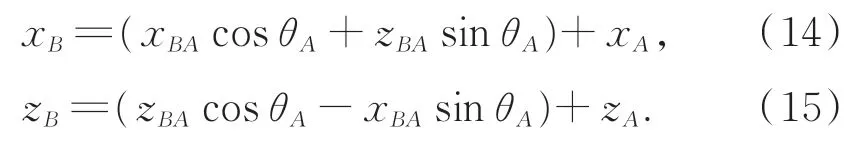
D点坐标:
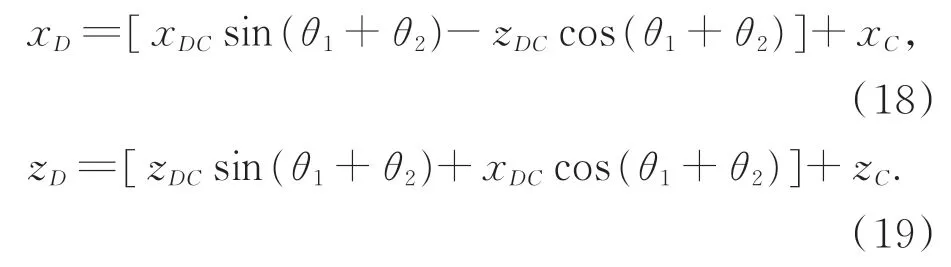
其余7根光纤的曲线情况可由相似的数学函数关系推导,所有测量点的空间坐标可以被获得并用MATLAB对空间离散点的插值拟合来重建三维形状。
4 结果与讨论
4.1 曲率标定试验
图5所示为柔性形状传感器及曲率标定实验设备。其中FBG波长解调器为自主研发,带宽为1 525~1 605 nm,波长解调精度为3 pm,用于实时记录测试时传感器中FBG的波长变化情况。测试时,为剔除环境温度变化对弯曲测试中FBG波长漂移带来的交叉耦合影响,实验室温度恒定在25℃。

图5 柔性形状传感器及曲率标定实验设备Fig.5 Flexible shape sensor and curvature calibration ex⁃perimental equipment
将柔性传感器平整无弯曲置于实验台上,并连接FBG解调仪来实时记录波长数据。对曲率分别为14.29,15.38,16.67,18.18,20,22.22和25 m-17个纯弯曲模型进行正弯曲标定测试。在对每个标定模型进行弯曲测试时,传感器应保持30 min左右,待FBG波长稳定后记录变化量,再将柔性传感器平整还原放置在实验台上,停止保存数据。待到FBG波长稳定到初始值时,对下一个标定模型进行标定测试。
通过读取FBG波长漂移量稳定后的值,得到柔性形状传感器对不同曲率的应变响应情况,如图6所示。可以得到,柔性形状传感器在进行曲率测试时,随着曲率的增大,柔性传感器植入的32个FBG的波长漂移量均呈线性递增趋势;而且,在测量同一个标准弯曲曲率标定块时,上层FBG阵列和下层FBG阵列的波长漂移量均保持良好的一致性,说明同杨氏模量下应变传递的稳定性。
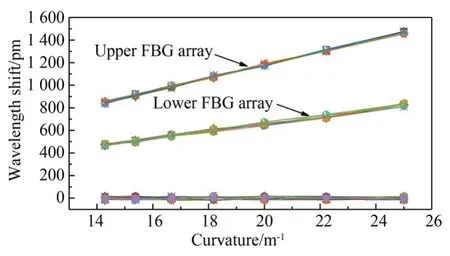
图6 柔性形状传感器对不同曲率的应变响应Fig.6 Strain response of flexible shape sensor to different curvatures
为了更直观反应柔性形状传感器对弯曲曲率的灵敏度响应,对上层FBG阵列和下层FBG阵列的波长漂移量进行算术平均,然后进行线性拟合,即可得到柔性形状传感器对弯曲曲率的灵敏度响应,如图7所示。由拟合函数可得,上层FBG阵列的灵敏度约为57.641 pm/m-1,下层FBG阵列的灵敏度约为32.250 pm/m-1,柔性形状传感器耦合稳定后的波长漂移量均表现为良好的线性度。由图7中线性拟合后的局部放大视图可知,在对上层FBG阵列进行正弯曲的曲率标定时,下层FBG阵列的波长变化量基本为0;在对下层FBG阵列行正弯曲的曲率标定时,上层FBG阵列的波长变化量基本为0,说明了FBG传感器在不受温度影响的前提下,只对轴向应变敏感,对纵向应变不敏感。
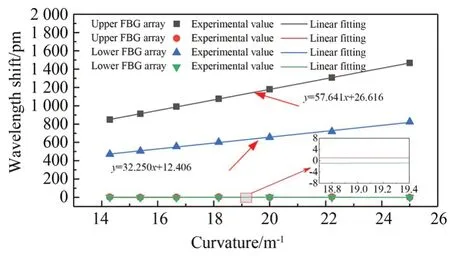
图7 柔性形状传感器对弯曲曲率的灵敏度响应Fig.7 Sensitivity response of flexible shape sensor to bending curvatures
4.2 三维形状测量与重建
为更加全面地研究柔性形状传感器对三维曲面的应变响应情况,采用Solid Works设计并3D打印了3个不同形状的测试基体,表面形状分别为等曲率曲面、波浪状曲面以及鼠标状曲面,在温度为25℃条件下进行测试。先将柔性传感器平整无弯曲变形置于实验台上,并接入FBG解调仪,实时保存波长数据。再将柔性传感器置于测试基体表面,紧接着用与测试基体相同尺寸的模型缓慢置于传感器上方以确保传感器与测试基体表面完整贴合。根据前期测试经验,保持30 min以上,待FBG波长完全稳定之后读取每个感测点的波长漂移值。将得到的32个FBG测点的波长漂移值代入理论推导公式转化为各测点的曲率信息,将曲率信息转化为各个测量点的空间坐标,再用MATLAB对空间离散坐标点的插值拟合来重建测试基体的表面形状。对其他两个测试基体同样采用上述步骤,测量结果如图8所示。由图可知,实验得到的图形与测试基体的表面形状基本保持一致,说明该柔性传感器能够感知被测物体表面的三维形状。
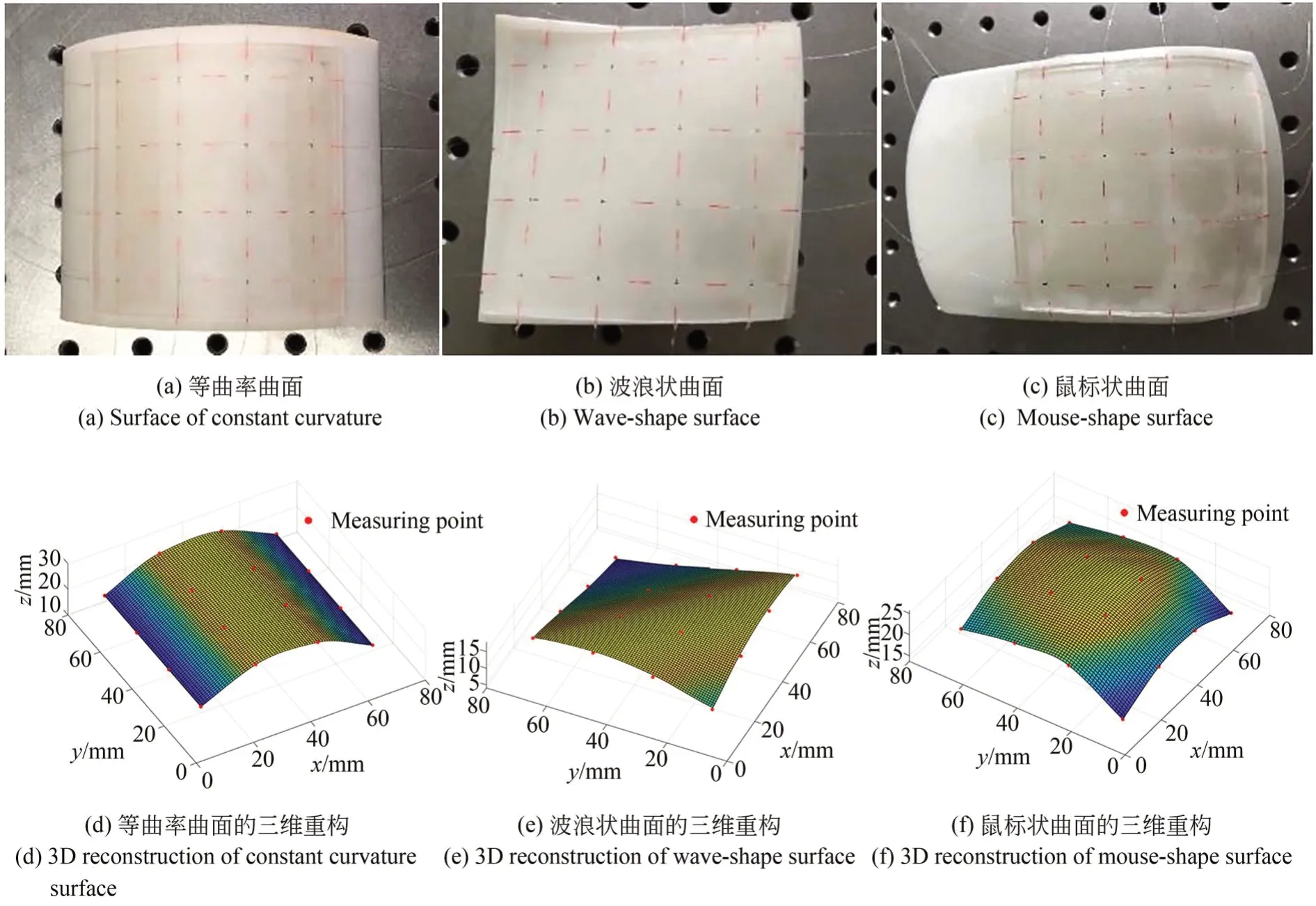
图8 测试曲面及三维重构图形等曲率曲面的三维重构Fig.8 Test surfaces and 3D reconstruction graphics of constant curvature surfaces
为得到柔性传感器的测量精度,将32个FBG测点的曲率代入误差计算公式ε=其中Pa为测试基体表面的实际曲率,Pe为柔性传感器实验测得的曲率。最大曲率的测量误差为4.5%,最小曲率的测量误差为2.8%,由此说明了该柔性传感器在进行形状测量时对测量点曲率感知的高精度性。
由图8中重构后的曲面可以看出,除了测量点之外,重建曲面的其他部分相对于被测基体仍然有不平整的部位,说明该方法只能还原被测基体表面的大致轮廓,并不能高精度地还原出被测基体的三维形状。分析认为误差来源主要有如下三个方面:
(1)重建算法误差。在本文推导的三维重建算法中,将植入的单个FBG当作是一个传感点,理论认为在有效的FBG检测区域内发生等曲率弯曲变形,而实际的FBG具有一定长度,实际情况中很难时刻满足FBG在检测区域内发生等曲率弯曲变形,必定会带来误差。该误差是系统误差,只能减小,不能消除;
(2)温度交叉敏感误差。虽然在室温恒定条件下进行测试,但传感器实验操作中,难免受到人手的触碰而带来局部温度变化;
(3)FBG布设误差。多个FBG双层阵列的布置中难免会存在工艺误差。
5 结 论
本文提出了一种基于双层正交FBG的可实现三维形状测量的柔性传感器。该传感器以PDMS为基体,上层和下层分别植入16个FBG阵列,构成32个FBG传感监测点。在室温下对该柔性传感器进行了曲率标定测试,得到了光纤光栅波长漂移量与曲率之间的线性递增关系。接着对柔性传感器进行了三维形状重建测试,将测量点光纤光栅波长漂移值转化为曲率值,再将曲率值转化为三维空间坐标值,最后通过对空间离散点的插值拟合,可视化地重建了测试基体表面的三维形状。结果表明:该柔性形状传感器可以实现对复杂曲面的三维形状感知,最大曲率测量误差为4.5%,可为软体机器人形状测量提供技术支持。后期将继续优化重建算法、结构以及FBG布设方式,探索软体机器人高精度形状测量的可行技术。
