后置分光瞳激光差动共焦曲率半径测量
2021-11-23李彦宏赵维谦邱丽荣
李彦宏,杨 帅,唐 顺,赵维谦,邱丽荣
(北京理工大学 光电学院 精密光电测试仪器及技术北京市重点实验室,北京100081)
1 引 言
在光学测量领域,球面光学元件作为光刻机、惯性约束核聚变装置等大型光学系统中应用十分广泛的光学器件,其曲率半径的检测精度会决定元件本身是否合格以及系统整体性能的优劣。随着技术的不断发展,球面光学元件曲率半径的检测除了保证较高的精度(10-5量级)之外,还必须简便、高效、低成本,因此以较低的成本实现球面光学元件曲率半径的高精度检测具有重要意义。
曲率半径测量方法分为接触式和非接触式两大类。接触式测量方法包括球径仪法[1-2]、三坐标法[3]和轮廓仪法[4-5]等,这些方法的精度相对较低、测量速度较慢,而且会对元件表面造成损伤,导致元件废品率上升。非接触式测量方法可分为干涉法和非干涉法。非干涉法由于受衍射极限的制约,测量精度仅能达到10-4,如刀口法和自准直仪法等[6]。相比之下,干涉法具有更高的测量精度,是目前应用最广泛的方法。随着研究的深入,基于牛顿干涉法[7]、F-P干涉法[8-9]、泰伯-莫尔条纹干涉法[10]以及菲索干涉法[11-12]的曲率半径测量方法被提出。
目前,最为常用且成熟的曲率半径测量仪器是ZYGO公司的菲索干涉仪,它利用机械移相分别对被测球面的猫眼位置和共焦位置进行定焦,进而得到待测曲率半径。共焦法[13]基于菲索干涉光路,其测量的相对标准差为2×10-5,然而衍射极限限制了共焦法的测量精度。本课题组于2010年提出了非干涉的激光差动共焦曲率半径测量方法[14],该方法基于差动共焦法研究出针对凹、凸曲率半径[15-16]以及特殊光学元件[17-19]的测量方法。然而,传统差动共焦法使用两路离焦量大小相等、方向相反的针孔和探测器,同时两个探测器的响应特性必须保持一致,测量误差较大,既增加了系统的造价成本,也增加了系统装调、校准的难度和时间。
本文提出后置分光瞳激光差动共焦曲率半径测量方法(Detecting Divided Aperture Laser Differential Confocal Radius Measurement,DDALDCRM),借助D型光阑将轴向双路离焦探测转化为焦平面上的单路离轴探测,通过算法实现虚拟针孔位置的选取,实现元件曲率半径的差动测量。与传统差动共焦法相比,该方法在保证测量精度的前提下减少一路探测系统,大大简化了光路结构,同时避免了复杂且耗时的系统装调过程,降低了系统成本。
2 测量原理
后置分光瞳差动共焦测量原理如图1所示。点光源S出射的光经过分光镜PBS和λ/4波片后被准直镜Lc准直为平行光,平行光束入射汇聚镜Ls后形成会聚的测量光束,当测量光束聚焦在被测透镜的猫眼位置和共焦位置时,其反射光束依次经过汇聚镜、准直镜和λ/4波片后被分光镜反射,形成探测光束。探测光束被D型光阑(D-type Aperture,DA)遮挡一半,透过的一半测量光束会聚在显微物镜(Microscope Objective,MO)的物平面上,并被显微物镜以放大率β放大成像在CCD探测面上。在探测器平面上设置两个圆形探测区域vph1和vph2,对称地设置在坐标原点的两侧,探测到焦前、焦后位置的轴向光强响应并进行差动处理。差动共焦响应曲线的零点精确对应被测球面元件的猫眼位置和共焦位置,利用激光干涉仪精确测得被测镜表面猫眼点和共焦点的轴向坐标ZA和ZB,这二者的间距d=zA-zB即为曲率半径R。
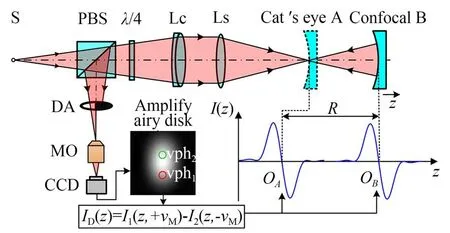
图1 后置分光瞳曲率半径测量原理Fig.1 Detecting divided aperture laser differential confo⁃cal radius measuring principle
在CCD探测平面上设置两个关于光轴对称的圆形区域vph1,vph2,其差动光强响应函数为:
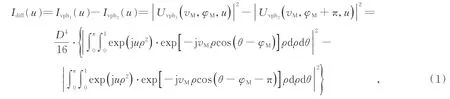
其中:u为归一化轴向坐标,v为归一化极径坐标,ρ0为归一化光瞳半径,D/fS′为汇聚镜Ls的相对孔径,fC′为准直镜Lc焦距,积分区域为半圆。
离轴探测原理为:光斑在焦平面上横向离轴,即焦前和焦后的探测位置与焦点探测位置不重合,如图2所示,显微物镜将D型光阑遮挡的一半测量光束放大成像于焦平面的探测CCD上,当被测镜在猫眼点或共焦点附近进行轴向扫描时,即归一化轴向坐标u从-2到2变化时,虚拟针孔vph1首先探测到焦前位置的光强信号,随后vph2探测到焦后位置的光强信号,便可使用一路探测光路实现对焦前、焦后位置的探测。将虚拟针孔vph1和vph2的轴向响应信号相减可以得到差动共焦曲线,利用曲线零点附近存在的线性区域进行直线拟合,计算得到绝对零点的位置坐标,实现高精度、高灵敏差动共焦定焦。
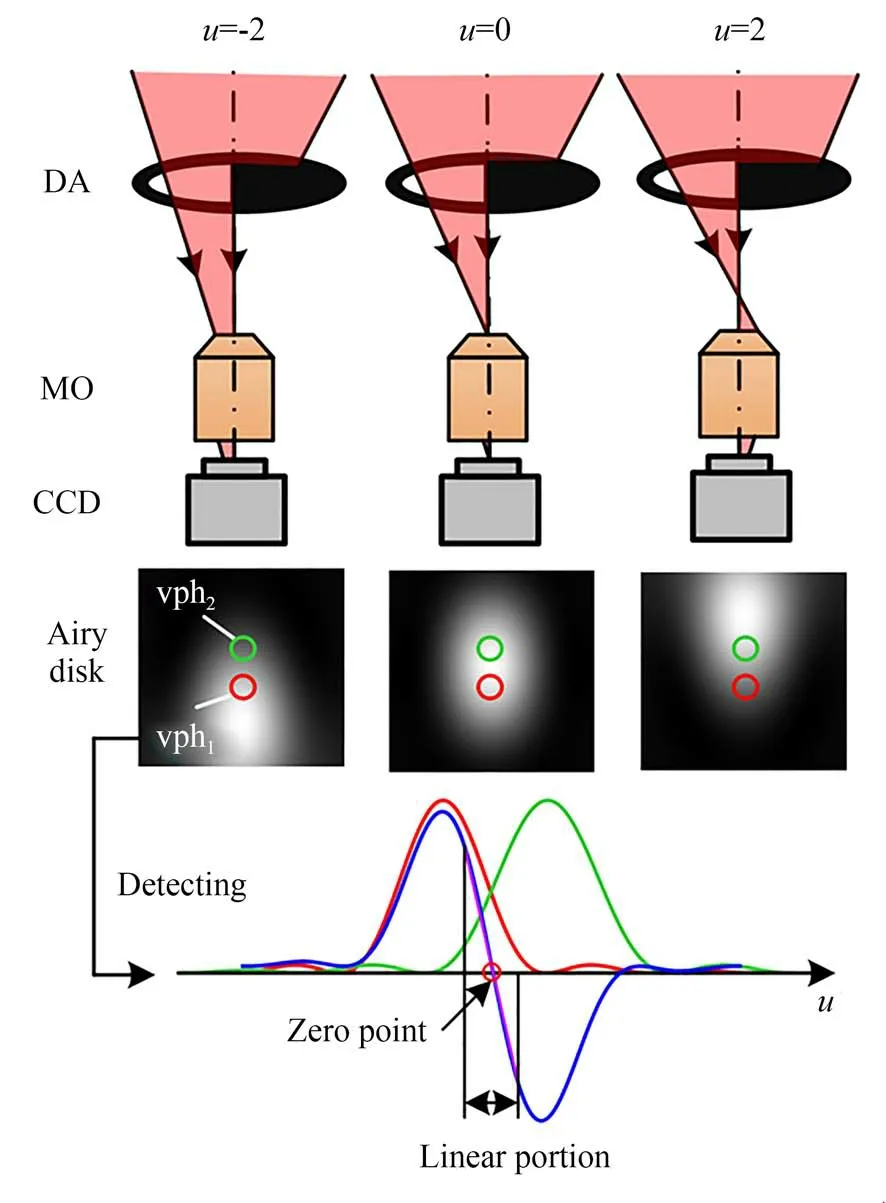
图2 D型光阑离轴差动探测原理Fig.2 Principle for off-axis differential detection using Dtype aperture
与传统差动共焦曲率半径测量方法相比,本方法采用位于焦平面的CCD探测,通过软件设置虚拟针孔实现对焦前、焦后位置的光强探测,可通过算法计算出CCD像面的像素位置坐标,使得虚拟针孔位置选取更加方便快捷,而且避免了物理针孔尺寸对定焦灵敏度的影响;利用D型光阑将轴向离焦探测转换为横向离轴探测,简化了测量光路,进一步降低了差动共焦曲率半径测量的装调难度和成本。
3 虚拟针孔定位算法
利用算法实现CCD虚拟针孔检测,对序列光斑图像计算质心坐标并拟合质心运动轨迹直线,然后确定虚拟针孔的对称中心以及离轴量大小和偏转角度,即可实现虚拟针孔vph1和vph2的定位,虚拟针孔定位算法流程和定位示意图如图3所示。
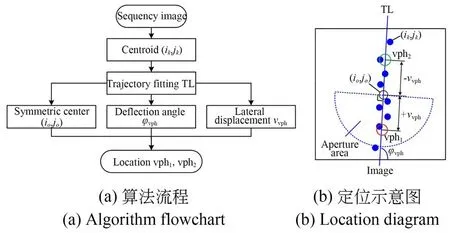
图3 虚拟针孔定位算法Fig.3 Virtual pinhole location algorithm
3.1 光斑质心计算
外界环境存在的杂散光被采集CCD所接收,采集光斑图像存在较多噪声,会影响光斑的质心计算,降低图像的信噪比。因此在计算质心坐标之前,对序列光斑图像进行预处理,得到信噪比较好的光斑图像。然后进行二值化处理,由于图像只有中间有光斑的部分的灰度值较大,四周的灰度值很低,可采用最大类间方差法(Otsu)实现对全局光斑图像的二值化处理。其主要思想为设置阈值将图像分割为目标部分和背景部分,当两部分的类间方差最大时,目标和背景的差别最大,二值化效果最好,由此计算出最佳阈值,得到光斑边缘轮廓。最后,利用重心法求得每幅光斑图像的质心坐标(ik,jk),其计算公式为:
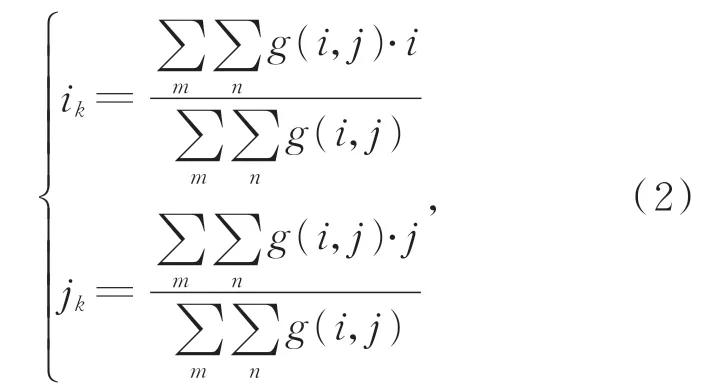
其中m,n分别为光斑图像横向和纵向的像素点数目。
3.2 质心运动轨迹拟合
在得到序列光斑的质心坐标之后,可以发现光斑的质心是沿某一方向运动,其运动方向与D型光阑的弦边垂直,即拟合的光斑质心坐标运动轨迹与D型光阑弦边的中垂线重合。考虑到实际应用时无法准确测得D型光阑的摆放角度,因此需要对采集到的光斑图像的质心运动轨迹进行拟合,间接求出质心的运动方向。利用最小二乘法对序列图像的质心坐标(ik,jk)的运动轨迹进行线性拟合,序列质心的横坐标记为I=(i1,i2,…,ik)T,纵坐标记为J=(j1,j2,…,jk)T,假设回归方程的矩阵表达式为:
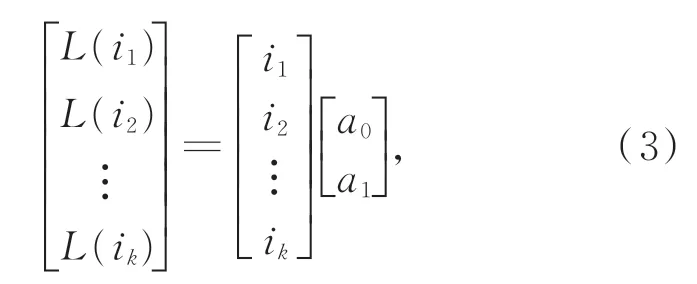
即L=AI,其中A=(a0,a1)T,则观测值J与拟合值L的偏差ε为:

最终求得序列光斑质心的运动轨迹直线TL。
3.3 确定对称中心和离轴量
理想虚拟针孔的对称中心应当是其焦点位置,在实际测量时并不知道焦点位置位于CCD像面的何处,因此将质心坐标灰度值g0(io,jo)最大时可近似看作其焦点位置,该质心坐标(io,jo)设为虚拟探针的对称中心。
对轴向响应曲线Idiff(u)求偏导得到差动共焦离轴量。当离轴量不断增加时,差动共焦曲线的定焦灵敏度随离轴量的变化曲线如图4所示,可以看出差动共焦曲线零点位置的归一化定焦灵敏度S(vM)在vM=4.2时最大,Smax(4.2)=0.517,此时差动共焦曲线具有最高的定焦灵敏度。此外,离轴量的大小与显微物镜的放大倍数和CCD的像元尺寸有关,虚拟针孔在CCD探测面上的最佳离轴量为:
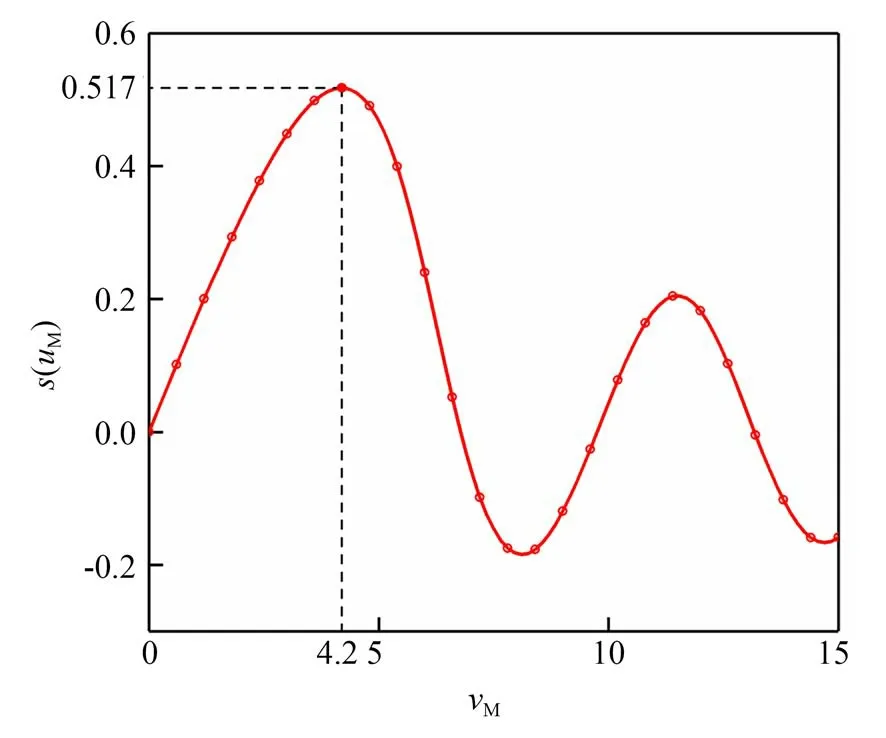
图4 定焦灵敏度随v M的变化Fig.4 Fixed focus sensitivity changes with v M
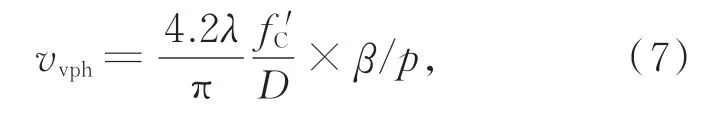
其中:fC′为汇聚镜Lc的焦距,D为汇聚镜Lc的通光口径,β为显微物镜的放大倍数,p为CCD的像元尺寸。
运动轨迹拟合直线TL与水平方向的夹角即为虚拟针孔的离轴量偏转角,即有:
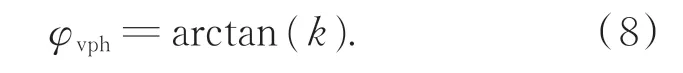
后置分光瞳差动共焦法主要通过程序设置对称中心、离焦量和偏转角这3个参数,由此可共同确定CCD探测面上虚拟针孔位置,进而实现单路离轴的差动共焦定焦测量。
3.4 虚拟针孔尺寸确定
假设探测器针孔的归一化半径为rp,实际点探测器得到的圆域内的光强响应可以看作是光强响应函数在以rp为半径的圆域的积分,则探测器探测到的平均光强响应信号为:
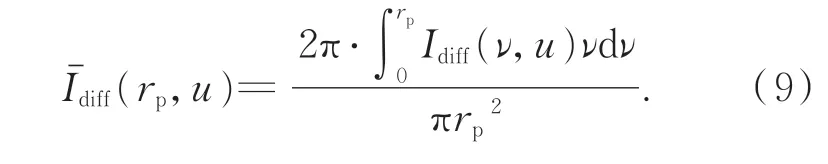
随着积分区域的变化,得到的平均光强也会有所不同。图5为定焦灵敏度S(vM)随归一化针孔半径rp的变化曲线。随着针孔半径的增大,定焦灵敏度下降。
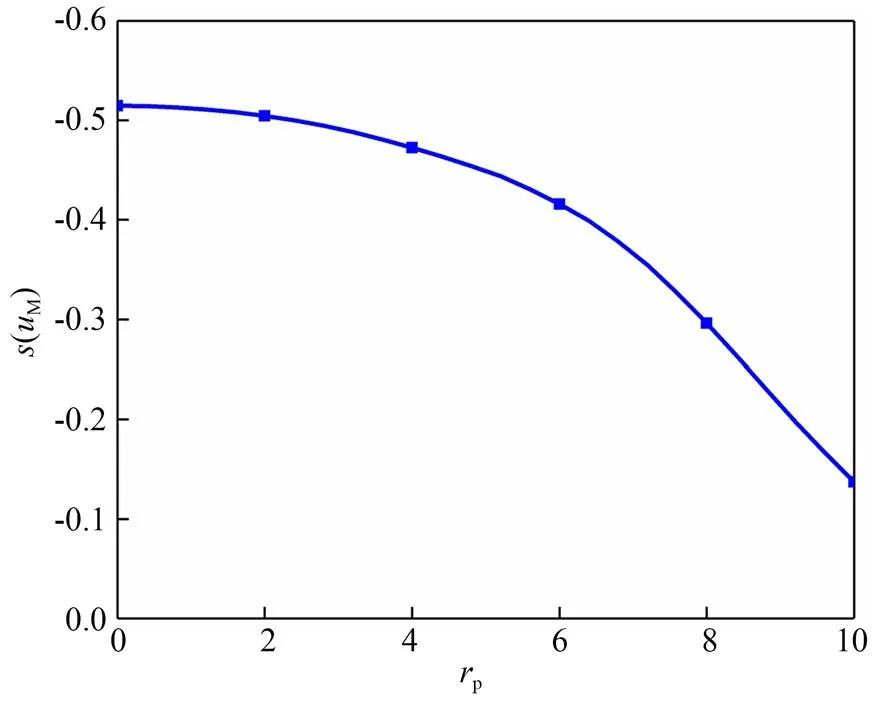
图5 定焦灵敏度随针孔尺寸的变化Fig.5 Variation of fixed focus sensitivity with pinhole′s radius
因此虚拟针孔的尺寸半径rvph也应很小,一方面需保证可采集到足够强的光强信号,另一方面以该区域的平均光强来描述虚拟针孔中心的光强信号,保证光强信号的准确性。选取以定位好的虚拟针孔的中心坐标为圆心,以rvph为半径的圆形区域,计算该圆形区域内的平均灰度值作为虚拟针孔的探测光强响应。在CCD探测面上的半径rvph与显微物镜的放大倍数β和CCD的像元尺寸p有关,此时的虚拟针孔半径rvph为:
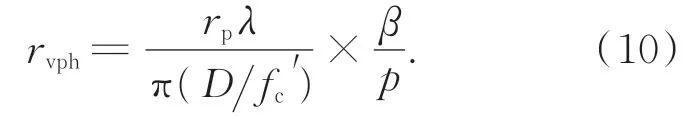
综合考虑,在保证零点的定焦灵敏度S(vM)不低于0.5时,虚拟针孔的尺寸半径越小越好。一般情况下,CCD探测面上的虚拟针孔半径rvph为3个像素为宜,此时对应的物理针孔半径rp约为1μm,既能使探测区域有足够的光强,也能使针孔尺寸足够小,保证了差动共焦的高定焦灵敏度。
4 测量实验与结果
为了验证本文方法的正确性及可行性,搭建后置分光瞳差动共焦测量仪器如图6所示。测量仪器主要由测量主机、直线导轨、五维调整架和测长干涉仪4部分组成。测量主机的光轴、气浮导轨运动轴以及测长干涉仪光轴严格同轴,将被测镜装卡与五维自动工作台上,通过气浮导轨在猫眼位置和共焦位置移动,测长干涉仪实时监测工作台的运动位置,整个实验装置放置于隔振平台上,隔绝环境振动对测量的干扰。实验在室温为(20.0±0.5)℃、湿度为42%±4%的环境下进行,被测件选用ZYGO F1.5的标准物镜,其外表面的曲率半径为-121.21 mm。

图6 后置分光瞳差动共焦曲率半径测量仪器Fig.6 Detecting divided aperture laser differential confo⁃cal radius measurement instrument
4.1 单点定焦及曲率半径重复性实验
首先对猫眼位置进行单点定焦实验,对测得的猫眼点的光斑图像进行虚拟针孔定位。选取CCD像面上坐标为(276,232)作为中心点,虚拟针孔vph1,vph2的中心坐标为(285,205)和(267,259),得到虚拟针孔vph1,vph2的光强响应曲线并进行差动相减处理,其虚拟针孔vph1,vph2以及差动共焦光强响应曲线如图7所示。利用猫眼位置差动曲线零点附近的约9.5μm(-0.001 7 mm,0.007 8 mm)的线性测量范围进行直线拟合,得到:
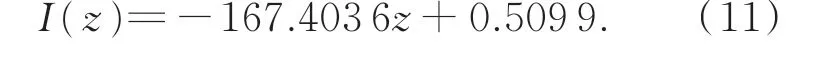
计算得到零点的位置坐标为0.003 0 mm,虚拟针孔vph1,vph2探测响应曲线的半高宽(Full Width Half Maximum,FWHM)约为15μm。与差动共焦法相比,此时的定焦灵敏度已达最高且无需额外调整硬件。
然后进行曲率半径的重复性测量实验。将被测镜移动到猫眼位置,测量此时的绝对位置zA,再次移动到共焦位置,测量此时的绝对位置zB,则曲率半径R=zA-zB,其中一次测量的猫眼和共焦位置的差动共焦曲线图7所示。
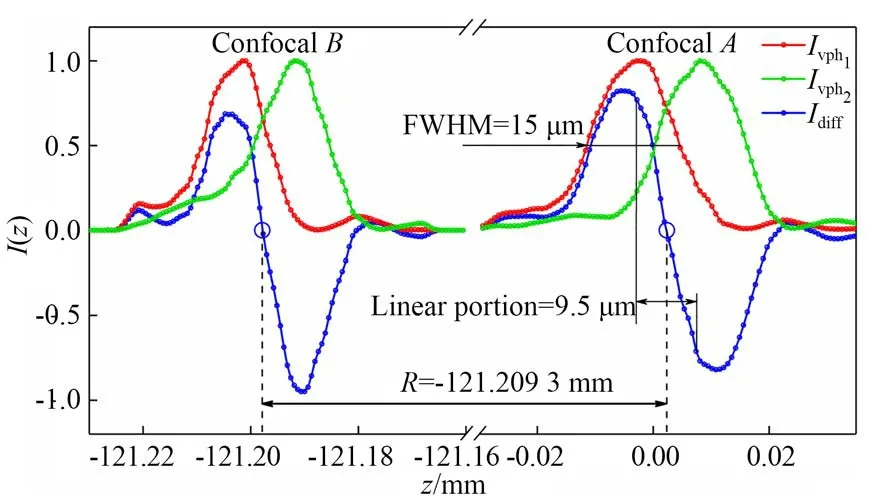
图7 猫眼点和共焦点的差动共焦曲线Fig.7 Differential confocal curves of cat′s eye point and confocal points
将后置分光瞳差动共焦的测量结果与差动共焦法的测量结果进行对比,两种方法重复测量10次的结果如表1所示。后置分光瞳差动共焦法的曲率半径测量结果的平均值为-121.209 4 mm,标准差为0.53μm;差动共焦法的曲率半径测量结果的平均值为-121.209 7 mm,标准差为0.39 μm,二者的测量结果相差0.3μm。
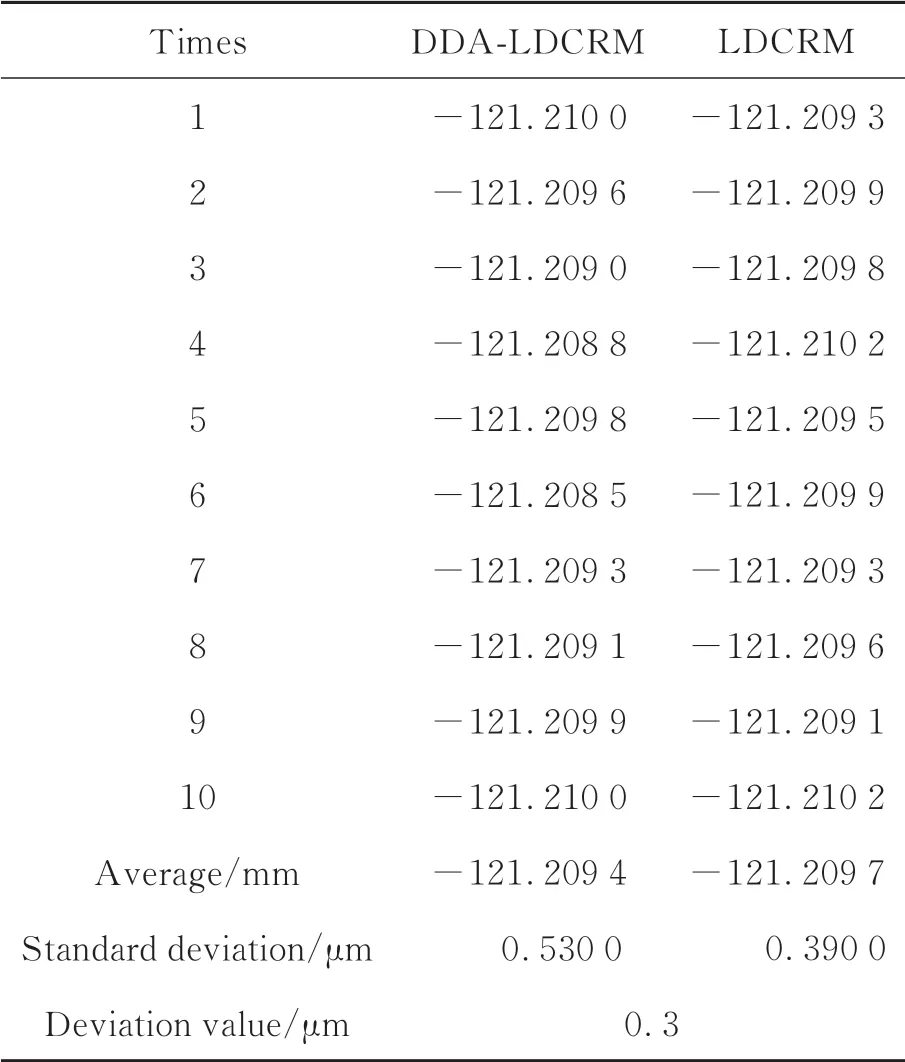
表1 曲率半径重复测量结果对比Tab.1 Comparison of repeated measurement results of radius of curvature
4.2 不确定度分析
与传统的差动共焦法相比,本方法采用一路探测光路实现差动共焦测量,避免了传统差动共焦由于两个探测器的离焦量不一致引入的测量不确定度。此外,除了激光干涉仪测长误差、测长激光光轴与系统光轴不同轴、面形误差、运动误差以及重复测量误差会引入不确定度,由于在探测光路中加入D型光阑,光阑偏心也会影响其定焦结果。
4.2.1 光阑偏心引入的不确定度
光阑偏心影响定焦灵敏度,由此带来了定焦误差,引入的不确定度为:
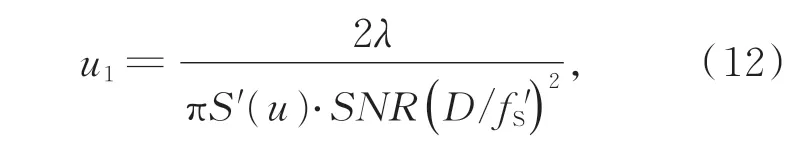
其中:SNR是数字显微镜探测器的信噪比,S′(u)为某一偏心量下的定焦灵敏度补偿值。此外根据公式还可以看出标准汇聚透镜Ls的相对口径D/fS′同样引入不确定度,物镜的相对口径越大,定焦精度越高,因此在测量过程中应选取相对口径合适的标准物镜来保证定焦精度。
4.2.2 测长误差引入的不确定度
进行位置监测的测长干涉仪采用了测量不确 定 度 高 达 ±0.5×10-6(k=2)的REN⁃ISHAW XL-80双频激光干涉仪,测长误差引入的不确定度为:
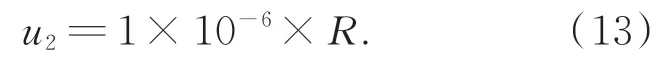
4.2.3 光轴不重合引入的不确定度
实际测量时,系统光轴和测长干涉仪测量轴线之间存在一定夹角γ,由此带来曲率半径测量误差。在CCD辅助下,γ角的调整精度可达4′,其不确定度为:
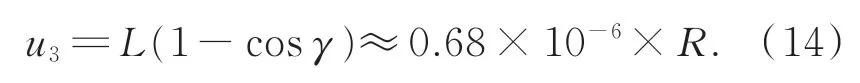
4.2.4 面形误差引入的不确定度
测量猫眼位置时激光汇聚于被测镜表面一微小区域,该区域与最佳参考球面不重合,会引入波长量级的误差,可用标准参考镜面形PV值测量来补偿误差,补偿后对被测镜曲率半径测量的不确定度为:
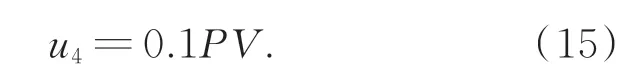
4.2.5 运动误差引入的不确定度
在实际测量时,由于导轨的直线度偏差,被测件在沿运动轴运动过程中相对测量轴发生径向平移,系统采用高精度气浮导轨,行程为1.5 m,运动径向平移精度可达3μm,径向平移误差引入的不确定度为:
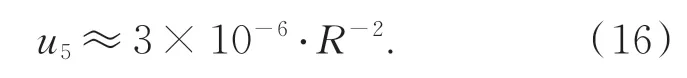
4.2.6 重复测量引入的不确定度
环境振动、气流、温度等因素也会造成测量误差,重复测量误差带来的不确定度为:
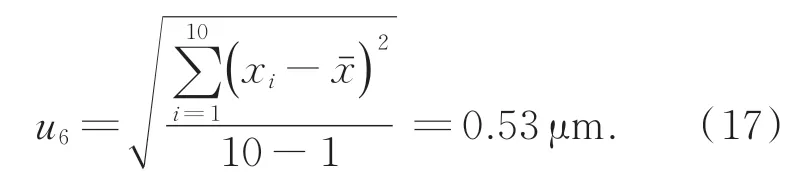
4.2.7 合成不确定度
上述不确定度分量相互独立,最终合成的不确定度为:
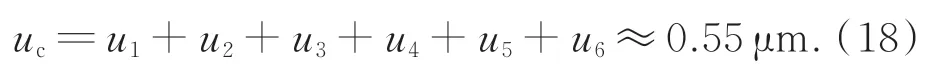
该标准球曲率半径测量结果的相对扩展不确定度为:
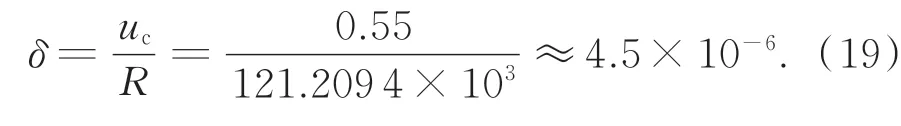
5 结 论
本文提出了DDA-LDCRM方法,阐述了基于虚拟针孔技术的后置分光瞳差动共焦定焦原理,研究出虚拟针孔定位算法实现单路离轴探测,然后构建DDA-LDCRM仪器,对仪器性能进行了实验验证。实验结果表明:10次测量曲率半径的平均值为-121.209 4 mm,重复性优于5×10-6。在满足曲率半径高精度测量需求之外,该方法舍去双路离焦探测装置,改为单路焦面探测,而且虚拟针孔的位置可以根据算法轻松调整,避免了传统物理针孔调整困难的缺点,极大地降低了系统装调的难度和成本,为高精度曲率半径测量提供了一条简便易行且成本低廉的途径。
