基于网络图拓扑结构的MILP模型求解智能制造系统中的工艺规划问题

刘齐浩，李新宇*，高亮

State Key Laboratory of Digital Manufacturing Equipment and Technology, School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China

1. 引言

智能制造包含智能制造技术和智能制造系统[1-3]。智能工艺规划（process planning, PP）属于重要的智能制造技术，在智能制造系统中扮演着重要的角色[4,5]。PP能够有效地缩短生产周期，提高产品质量，并进一步降低资源和能源的消耗[6]。因此，PP在工业应用与研究中获得了较多的关注。然而，因为PP问题内部存在着大量的柔性，导致在实际生产场景中很难得到最优的工艺规划路线[7]。

解决传统的PP问题通常需要三个步骤：工艺选择、资源分配和工序排序[5]。通过第一步的工艺选择来确定不同加工特征所需要的工艺及工序，并基本确定工艺路线的总长度。然后，通过分配机器、刀具等资源，来确定各工序的加工资源分配，预获取相关加工参数，例如加工时间等。最关键的工序排序一般是最后执行，且排序过程必须遵循该工件工艺网络图中的优先关系约束[8]。例如，粗铣工序和粗磨工序必须安排在精铣工序和精磨工序之前执行，镗孔工序必须排在钻工工序后[9]。

PP问题已经被证明是非确定性多项式时间困难（nondeterministic polynomial-time-hard, NP-hard）问题[6,10]，这也意味着仅仅依靠传统的梯度下降法、图论法和仿真方法很难实现PP问题的求解。因此，多数研究者试图引入元启发式算法来求解PP问题[11]。当前主要的求解方法包括遗传算法（genetic algorithm, GA）[7,12]、禁忌搜索算法（tabu search, TS）[13]、粒子群优化算法（particle swarm optimization, PSO）[8]、蚁群优化算法（ant colony optimization, ACO）[14]和蜜蜂配合优化算法（honey-bees mating optimization, HBMO）[10]。这些算法能够在较短时间内获得近优解，更侧重算法的求解效率而不是解的最优性。

在此研究背景下，大部分公开PP问题的最优解至今还未找到[8,15]。其中一个重要的原因是当前研究更多关注的是如何提高智能算法的性能，而不是去研究问题的数学模型，尤其是混合整数线性规划（mixed- integer linear programming, MILP）模型[14]。有效的MILP模型能够通过数学规划求解器求解，如CPLEX、Gurobi等，并在一定条件下稳定地获得最优解。但是，模型的求解效率与问题的规模相关，随着问题规模的逐渐增大，模型的求解效率会迅速降低，甚至在相当长的计算时间内无法获得可行解[16]。这也是当前PP的研究重点不在模型上的重要原因。此外，当前PP的MILP研究还处于一种“妥协”状态，即当前模型都是基于工艺特征建立的[8,14,17]。这种类型的模型通过将原始工艺图转换成工艺特征表来简化表达，但是这种转化会改变工艺网络图的原始信息，甚至改变原问题的解空间结构而导致最优解的丢失（该部分的讨论将在第3.3节展开）。当然，也有一些建模方法能够规避上述情况的发生，但它需要复杂的前序处理操作[18]，而当工件的工艺网络图较为复杂时，这种前序处理操作会非常繁琐费时。

为了添补当前研究工作的空白，本文提出了一个全新的基于PP网络图拓扑结构的MILP数学模型，本文的主要贡献如下：

（1）与现有研究中的模型相比，本文所提的基于网络图OR节点的MILP模型不需要任何工艺特征转换或前序处理操作。

（2）工序的优先关系在本文中进行了详细的讨论，并提出了三种优先关系模型来分析论述工序的优先关系约束。

（3）通过通用代数建模系统（general algebraic mode- ling system, GAMS）调用CPLEX求解器对所提模型进行求解，成功得到了现有文献中大部分开放问题的最优解[8,15,16]。

本文的后续部分组织如下：第2节介绍相关的研究；第3节介绍所提的模型细节和上文所提的相关分析；第4节是验证实验部分，验证所提模型的优越性；第5节则进行了总结和对未来工作的展望。

2. 相关理论与研究介绍

关于PP问题的研究主要可以分为两类：算法相关的研究与模型相关的研究。Xu等[6]和Leo Kumar [4]在PP问题上已经做了很全面的综述工作。智能算法，如GA、模拟退火（simulated annealing, SA）算法、TS算法和PSO算法已经在解决PP问题上展现出了足够的优势，并且已经广泛地应用到该问题的求解中。为了求解复杂棱柱形零件的PP问题，Li等[19]提出了一种由GA和SA组成的混合算法。通过基于Hamming距离的解搜索和选择策略，该混合算法的局部搜索能力得到了有效的加强。Hua等[20]基于GA提出了一种合成算法来搜索PP问题的最优或近优解。Li等[15]提出了一种有效的基因编程（genetic programming, GP）算法，来操作工艺网络图中的OR节点支路。考虑刀具和进给速度等制造资源的选择，Shin等[21]提出了一种共生进化算法来优化三个目标，包括机器负载平衡、零件移动最小化和换刀次数最小化。Wang等[22]提出了一种包含两类局部搜索策略的PSO算法求解PP问题，也取得了不错的效果。后来，Li等[8]也提出了改进的PSO算法来求解考虑工件转运时间的PP问题。Liu等[14]将ACO算法与问题的约束矩阵和状态矩阵结合，并成功应用于求解两类柱状零件的PP问题。

虽然智能算法解决PP问题方面取得了一些成果，但由于元启发式算法不能保证解的最优性，所以在大多数现有PP实例中，解的质量还可以通过数学模型进一步提高甚至优化到最优。此外，数学模型作为一种问题的表述方法，能够帮助研究者进一步地理解和探索问题[23]。因此，进行PP问题的模型相关研究意义深远。Floudas和Lin [24]基于时间表示方法，分析研究了几种PP的混合整数规划（mixed-integer programming, MIP）模型，并提出了几种有效的优化方法来提高模型的计算效率。着眼于PP与调度的互补属性，Li等[25]建立了PP与调度集成的数学模型。Xia等[26]基于工艺特征的思路提出了可重构PP问题的数学模型。同样是基于工艺特征的方式，Jin和Zhang [16]建立了考虑机器间转运约束的PP问题的数学模型。

据目前调研所知，现有的PP问题数学模型都是基于工艺特征建立的[8,14,17]。虽然这种表示方法能够描述大部分类型工件的工艺，但是仍然不可避免地加入一些本来不存在的工序紧前关系约束[16]。与之相比，本文所提的基于网络图的表示法比基于特征的表示法更能表示原有的工艺信息，而不会添加额外信息。本文提出了一个直接基于工艺网络图拓扑结构的MILP模型，该模型能够描述所有类型的PP制造柔性，而不添加或遗漏任何约束。通过求解所提模型，成功获得了一些著名数据集的新最优解。

3. 工艺规划MILP数学模型

3.1. 问题描述

图1. 工艺网络图示例。OR1、OR2、JOIN1、JOIN2分别表示1号OR节点、2号OR节点、1号JOIN节点和2号JOIN节点。

PP问题中包含的柔性类型有工艺柔性、机器选择柔性和工序序列柔性，常用的表示方法有Petri网络[27]、工艺特征表[28]、AND/OR图和网络图等[29,30]。图1为某工件的制造柔性通过网络图表示的示例，网络图由5类节点构成：虚拟的开始节点和终止节点，表示加工的开始和结束；表示工序的中间节点；以及配合起来表示工艺约束的OR节点和JOIN节点[15]。中间节点包含工序序号、可选加工机器号以及对应的加工时间三种信息。例如，中间节点6表示的是工序6能够在序号为3、7和13的机器上加工，且对应的加工时间分别为44、48和49。这里的加工时间单位按照原始数据被省去。被箭头链接的两两工序之间有着优先关系约束[21]，如图1中节点2和3之间的箭头表示工序2必须在工序3之前加工。而没有箭头链接的工序之间不存在这种优先关系约束。此外，介于一对OR节点和JOIN节点的支路只能有一条被选择，包含在支路里面的工序配合其他工序组成一条可行的加工路线[29]。以图1为例，如果节点OR1和JOIN1之间选择支路2 → 3，节点OR2和JOIN2之间选择工序7，则其中一条可行的加工路线可以是：1 → 2 → 3 → 5 → 6 → 7 → 9 → 10。

3.2. 工序间的优先关系

根据模型中0-1二元变量的定义，PP问题的建模方式可以分为三种[31]：

变量θjt会引入比其他两种类型更多的派生变量和约束，因此现有的PP问题建模研究中鲜少提及。基于位置的变量ρjt描述的是工序在一条序列中的位置序号[16,32,33]，被较多地应用在现有的模型相关研究[24,34,35]中。作为对比，本文所提的MILP模型则是首个基于第三种类型变量qjj′建立的模型。

以图2中网络图表示的工件为例，其中一条可行的加工路线为：1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9。因为工序1在其他所有工序的前面加工，所以根据变量q1j′的定义可以得出：q1j′= 1，其中j′ = 2, …, 9。工序2在工序3到工序9前面加工，因此q2j′= 1，其中j′ = 3, …, 9。 以此类推，矩阵Q = [qjj′]中等于1的变量总数为(n - 1)n/2， 其中n表示工序总数，同样也等于该工序序列的总长度。图3展示了由工序序列生成Q矩阵的过程。

在一条已经确定加工顺序的序列中，任意两两工序之间都存在一个优先关系。因此，可以通过一个n × n矩阵来表示一条工序序列中包含的所有优先关系，即上述的矩阵Q。矩阵Q可以被看作是工序序列优先关系的完全表达矩阵（completely expressing matrix, CEM），因为它包含了一条序列中所有的优先关系。通过观察和分析发现，CEMQ的特征约束可以总结如下：

（1）CEMQ对角线上的元素都等于0。

（2）关于对角线对称的两元素之和等于1。

图2. 工艺网络图实例。

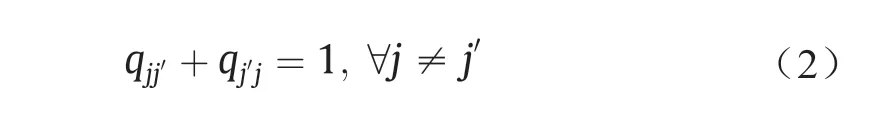
（3）任意两列元素之和互不相等。

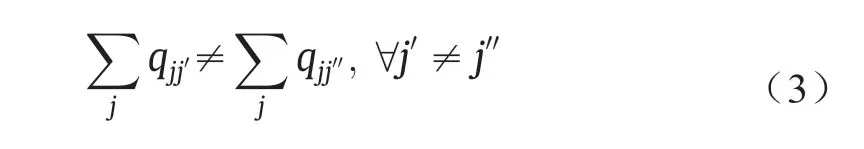
式（1）指代的是优先关系只存在于两个不同工序之间。式（2）指代的是两工序之间只能存在一种优先关系。CEMQ中的每列元素之和等于该列对应工序在序列中所处的位置序号，根据位置的唯一性推断出式（3）成立。CEMQ矩阵包含了一条序列的所有优先关系，可以根据序列的CEMQ来判断该序列是否满足网络图中的优先关系约束。

引入符号sjj′来表示图2中网络图的优先约束：

根据定义，对应的矩阵S= [sjj′]如图4所示，其中S矩阵中的“1”对应于网络图中的箭头，表示优先关系约束。如果一条工序序列满足工艺网络图中的优先约束，则其序列的CEMQ应该与矩阵S有如下关系：

矩阵S可以从网路图中生成，但是在序列未定前，CEMQ则是未知的。由此，式（4）是用来约束未知的CEMQ的。

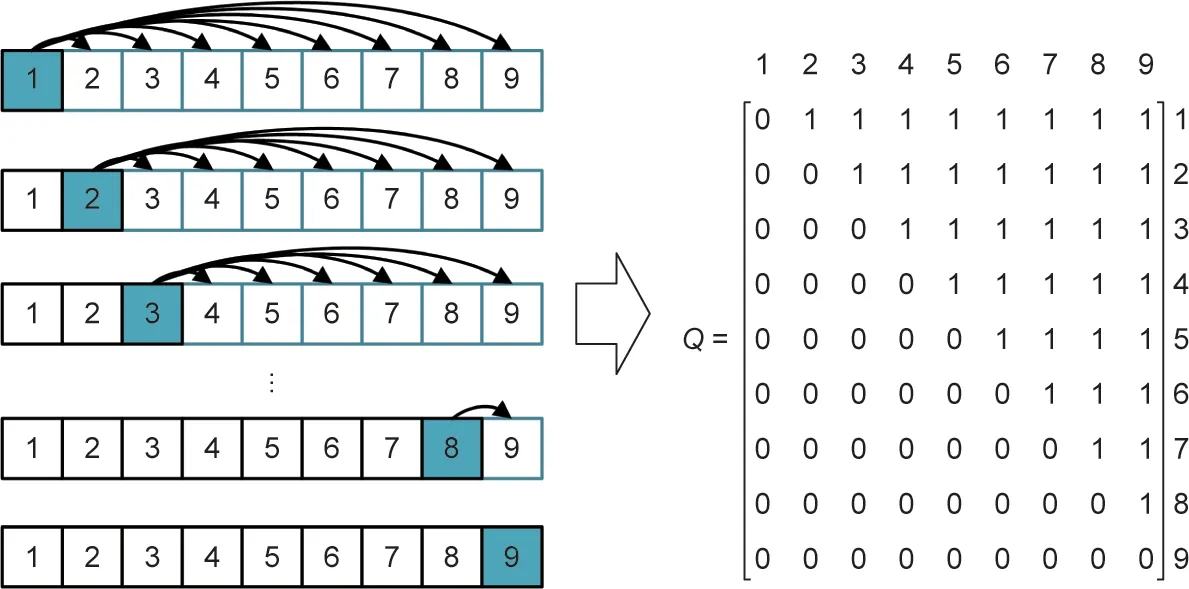
图3. 优先关系矩阵转换示例。

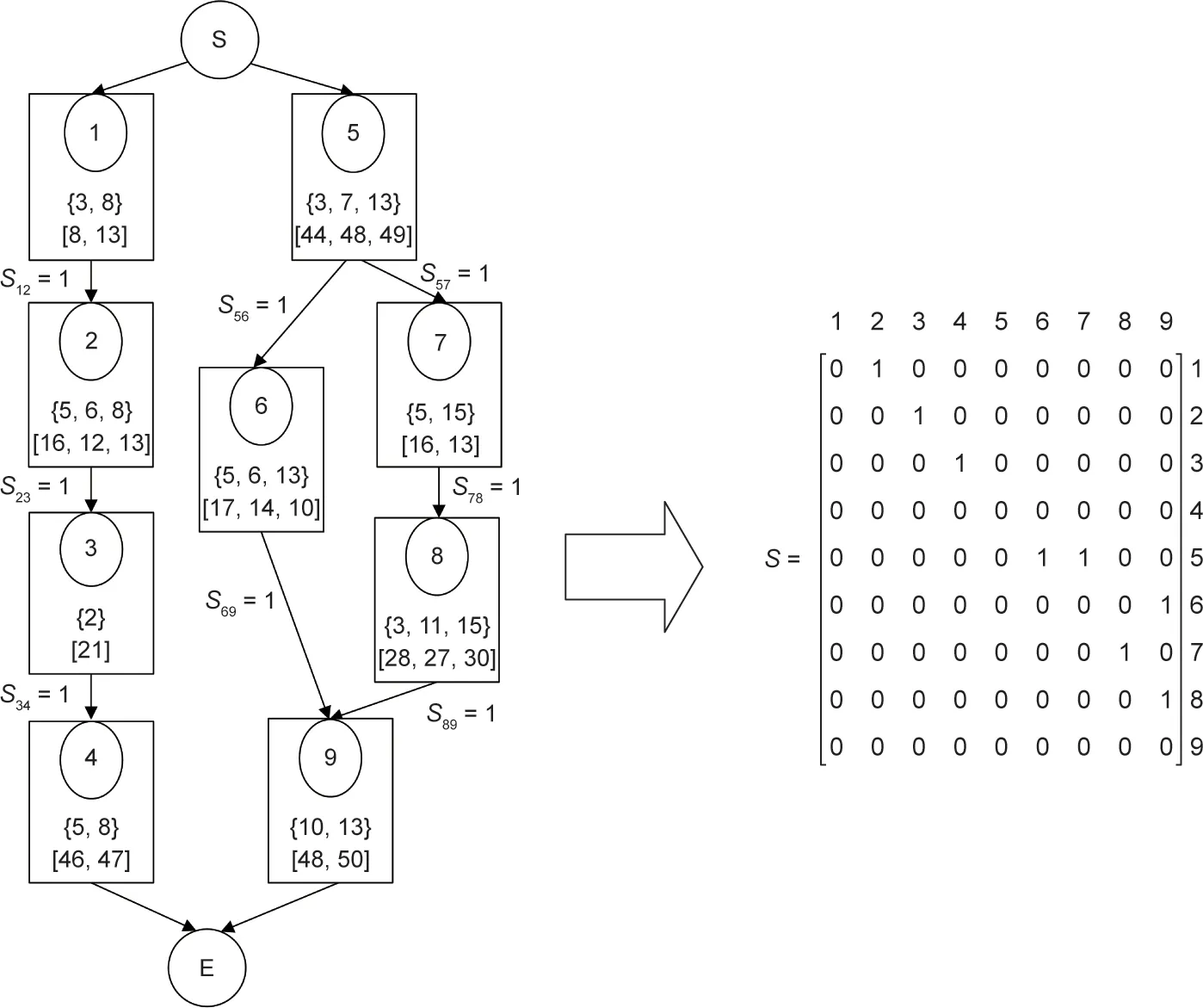
图4. 网络图中的优先约束和对应的矩阵S。

CEM中等于“1”的元素数量为(n- 1)n/2，但是并不意味着定义一条工序序列需要(n- 1)n/2个 “1”。实际上，定义一条序列所需的最小“1”总数为n- 1个。以序列1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9为例，只需要定义两两相邻的元素之间的优先关系，就可以确定该 序 列，即q12、q23、q34、q45、q56、q67、q78、q89等 于1即可。从这点出发，定义一个包含等于1的变量数最少的矩阵V = [vjj′]，有利于简化工序优先关系的研究。基于上述讨论，矩阵可看作是精确表达矩阵（exactly expressing matrix, EEM），包含定义一条工序序列所需要的最精确和最少的等于“1”的变量。上述工序序列的EEM V如图5所示。

因为EEM V包含所有紧邻工序之间的优先关系约束，所以EEM V同时也能被称作紧前关系矩阵。根据直接紧邻关系，可以较为容易地通过依次读取EEM V中等于1的元素来获得一条工艺路线，完成矩阵到序列的转化。EEM V的特征约束如下：

（1）EEM V中等于1的元素总数等于n - 1。

（2）EEM V的行和列中最多只能有1个元素等于1。

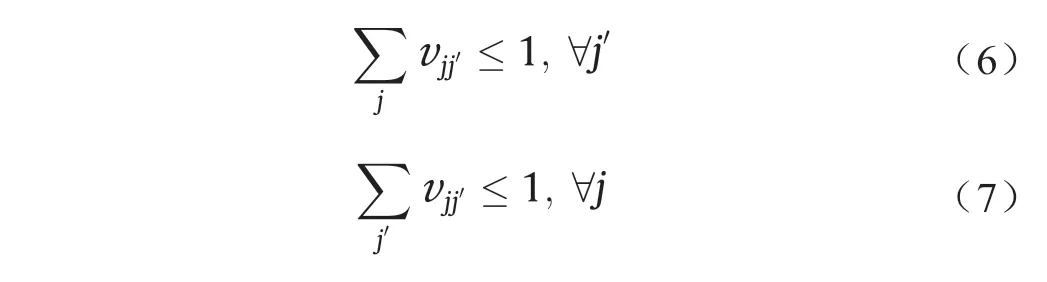
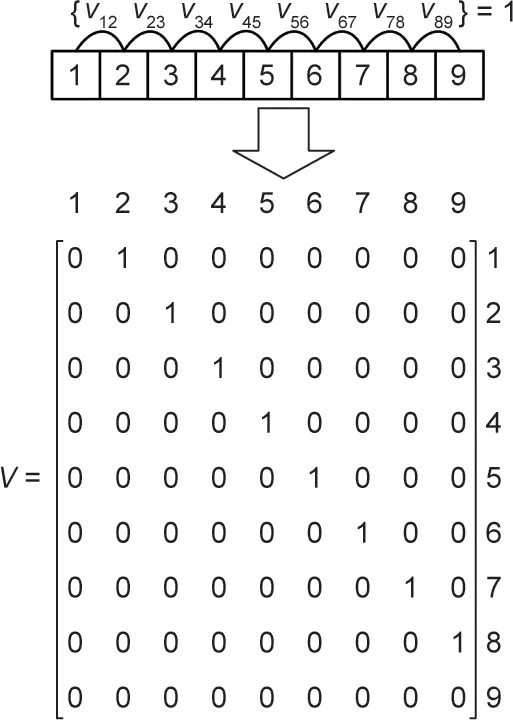
图5. 序列的精确表达矩阵。

（3）CEM Q与EEM V之间的关系如下。

EEM V是CEM Q的简化表达形式，并且二者都能够定义一条唯一的工序序列。由于矩阵S中对序列优先关系的不完整表示，使其不能定义一条唯一的工序序列。因此，在本文中矩阵S也可以被称作优先关系的部分表达矩阵（partly expressing matrix, PEM）。不难得出，一般情况下不止一条工序序列可以满足由PEM S表达的优先关系约束。CEM Q、EEM V、PEM S的对比如图6所示。

3.3. 关于工艺特征表示法与工艺网络图表示法的讨论

现有文献[8,16]中关于PP问题的模型都是基于工艺特征表示法建立的，如图7（a）中的以工艺特征表表示的算例。实际上，该算例是由文献[29]中的第18个算例通过转换得到的，如图7（b）所示。图7（a）、（b）表达的是同一件工件的工艺信息。

在特征表[8,16]中，工艺特征F2、F5和F9有着可选的加工工序或加工工序集合，分别与网络图中的三对OR及JOIN节点相对应。然而不同的是，特征表中同一工艺特征下的工序集合会被紧前关系约束，而这种约束在原始的网络图中却是不存在的。例如，如果工艺特征F2选择了通过工序集合O4～O5来实现，那么在生成的工序序列中O5必须在O4完成加工后立刻开始加工。但是，根据网络图图7（b）传达的工艺信息，是不存在这种立刻开始加工的必要的。这种多余的捆绑可能改变原始的解空间结构，导致失去找到最优解的可能；而实际上这个算例就是如此。表1分别展示了通过基于特征的模型和基于网络图的模型所求得的最优解工序序列，其中带数字下标的字母M表示的是工序的加工机器号。

观察表1，由基于工艺网路图模型得到的序列可知，工序O4和O5之间不存在紧前关系约束。此外，基于工艺网络图模型获得的最优解356优于基于工艺特征模型获得的最优解357。其实，因为受到了紧前关系的约束，通过工艺特征构建的问题解空间是原始网络图表示的解空间的子集。由此可知，直接根据工艺网络图建立问题的模型要好于基于工艺特征表的方式。

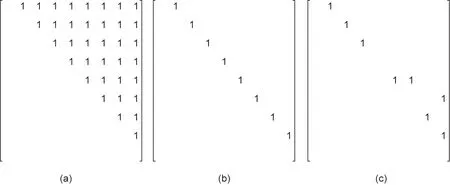
图6. 三类优先关系矩阵。（a）CEM Q；（b）EEM V；（c）PEM S。

图7. 同一算例的两种表现形式。（a）工艺特征表；（b）工艺网络图。

表1 工艺特征模型与工艺网络图模型求得的最优解

通过工艺特征表表示的PP问题的工艺柔性是通过同一加工特征下可选的工序和工序集合实现的，而工艺网络图表示的PP问题则是通过选择连接在OR节点上的支路实现。每条支路对应于工艺柔性的一种选择。如图8所示，OR节点与JOIN节点的序号是自上而下、自左而右的。如果选择了OR节点1的支路1，那么工序2、3和4则一定会被选择，此时无论OR节点2选择支路1还是2，工序5、6、7和8都不会被选择。这是因为，工序5、6、7和8不仅被OR节点2控制，还被OR节点1的支路2所控制，而OR节点1的支路2并没有被选择。OR节点支路选择有效的前提是该节点位于的支路被选择。

引入二进制参数wjrl来描述OR节点对工序节点的控制功能，参数wjrl定义如下：

以图8为例，对应的wjrl参数值如表2所示。

表2 参数wjrl值

综上，可将OR节点的控制功能归纳如下：当且仅当控制工序j的所有支路都被选择，工序j才会被选择；否则，只要当其中一条控制支路未被选择，工序j就不会被选择。引入0-1二元变量url来描述OR节点支路的选择状态，同时引入0-1二元变量xj来描述工序的选择状态。变量url和xj的定义如下：

第3.4节介绍的模型是基于上述两种变量url和xj以及参数wjrl展开的。

3.4. PP问题的数学模型

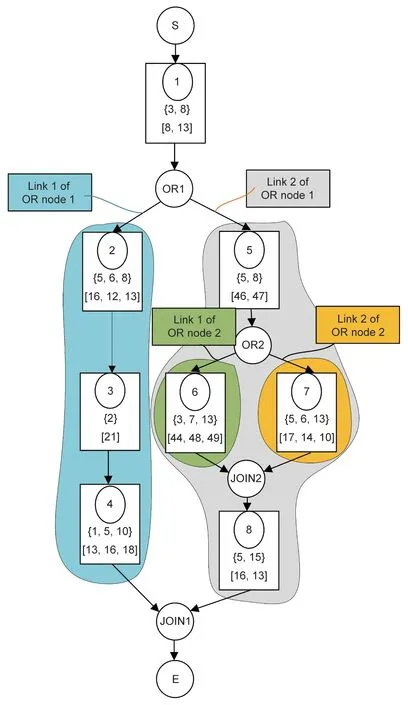
图8. OR节点控制功能的讨论示例。

本文中MILP模型是基于优先关系和网络图OR节点的。大部分的工艺优化目标都是时间相关[8]或者成本相关[14,18]的，本文的优化目标为最小化总生产时间，并且考虑工件在机器间的转运时间约束。模型的集合、下标、参数以及变量展示如表3所示。

表3 PP问题数学模型的集合、下标、参数以及变量定义

总生产时间为模型的目标函数：

式（9）右边的第一部分是工件的总转运时间，第

二部分是工件的总加工时间。模型的约束如下：（1）OR节点约束。

式（10）表示的是被OR节点控制的工序不被选择的前提条件：只要有一条控制工序j的支路未被选择，工序j就不会被选择。式（11）表示的则是工序被选择的前提条件：工序不被任何OR节点控制；或者，控制该工序的所有支路都被选择。式（12）表示的则是工艺柔性只能选择连接在一个OR节点上的所有支路中的一条。

（2）工序优先约束。

式（13）～（18）表示的是工序之前的优先约束。与式（1）～（4）不同的是，在这组约束里加入了工序被选择的前提。式（13）对应式（1），式（14）、（15）对应式（2），式（16）对应式（3）。式（17）表示如果工序j和j′未被选择，那么qjjʹ和qjʹj都被设置为0。式（18）则是确保被选中的工序遵循网络图中的优先关系约束。

（3）EEM V与CEM Q约束。

因为矩阵V只包含两相邻工序的优先关系，工件相邻工序的转运时间可以借此计算。式（19）～（22）描述的是矩阵V的自身属性，及矩阵V和Q之间的关系。

（4）机器选择约束。

式（23）表示的是被选工序只能选择一台机器执行加工，且未被选择的工序无须分配机器加工。

（5）转运时间约束。

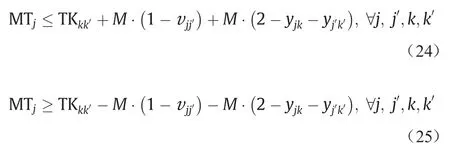
式（24）和（25）表述了工序j从当前处理机器到下一个机器的转运时间。

4. 实验与讨论

通过5组由著名数据集组成的数字实验来验证MILP模型，所得结果直接与文献报道的其他方法所得的结果比对。实验平台配置3.7 GHZ和16 GB 随机存取存储器（RAM）的个人计算机，模型通过GAMS编码并调用CPLEX进行求解。引入Gap值（%）来评价模型所求解的质量，该值表示所得解的相对偏差，定义为(BF - BP)/BP，其中BF为目标值的当前最好解，BP为当前下界。Gap值越小，表示当前解越接近理论下界，即质量越好。求解时间设置为3600 s，如果在该时间内未搜索到最优解，计算进程就会被中止，并且当前解会被输出。实验1、2、4和5中机器间的转运时间数据来自文献[8,18]，如表4所示。

表4 机器间的转运时间矩阵[8,18]

4.1. 实验1

实验1中的3个算例来自Jin和Zhang [16]，他们提出类似动态规划（DP）-like的启发式算法。本文中MILP模型获得的结果与DP-like启发式算法所得结果对比如表 5所示。第一个对比算例中MILP模型获得的解目标值为357，好于DP-like启发式算法获得的解目标值360。此外，MILP模型能够获得并证明全部3个算例的最优解。

表5 实验1的结果对比

4.2. 实验2

实验2的4个算例来自不同的文献：算例1来自Zhang和Lee [36]，算例2～4来自Li和McMahon [37]。算例的详细数据可见原文献。算例的对比结果为Li等[8]提出的改进PSO算法是当前求解此类组合优化问题最有效的算法之一。对比结果如表6所示，MILP模型能够获得目标值更好的解，并且以较短的计算时间（小于1 s）获得了算例2～4的最优解。

表6 实验2的结果对比

4.3. 实验3

本组实验的两个算例来自Li等[15]提出的GP算法，机器转运时间矩阵如表7所示。两个算例唯一的区别是算例2中的机器2被移除。实验对比结果如表8所示，GP算法和MILP算法都能找到两个算例的最优解。

表7 机器间的转运时间矩阵

表8 实验3的结果对比

4.4. 实验4

本组实验的17个算例来自著名的Kim数据集[29]，由18个工件组成，其对比的算法和结果来自文献[8]。由于文献[8]中工件4的算例数据有问题，因此在本组实验中不予展示。MILP模型与改进的PSO算法、GA和SA算法的对比结果如表9所示。在可接受计算时间内，MILP模型能够找到本组17个算例中的13个最优解。对于未找到最优解的算例，模型所得解的质量也好于对比算法解的质量，如算例3、6、12和15。

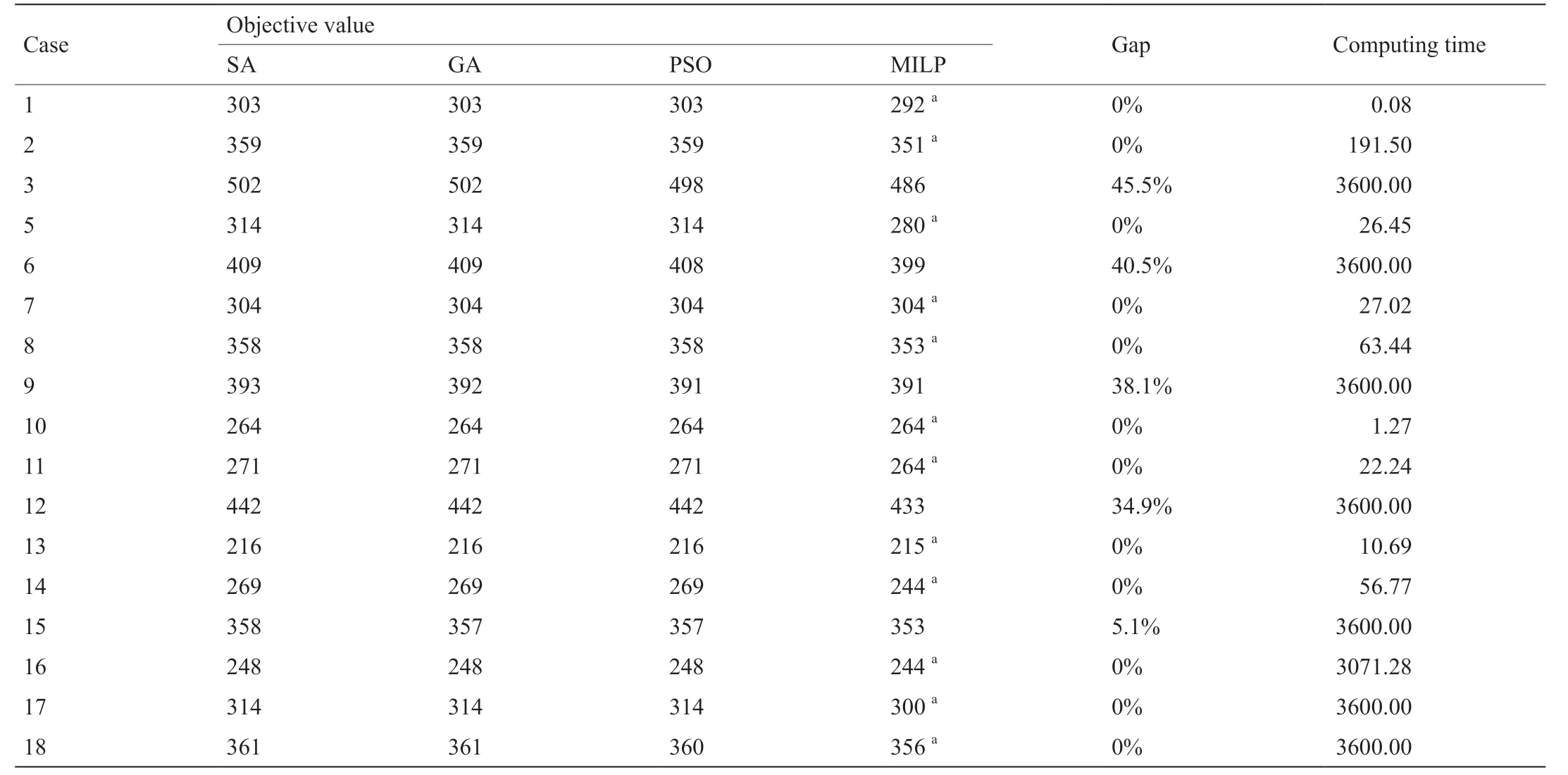
表9 实验4的结果对比

4.5. 实验5

实验5的11个算例来自另一组有名的Shin数据集[21]，其对比计算结果同样来自Li等[8]。因为同样的数据问题，略去了工件9、10、12、13、15、17和18的对比。MILP模型与改进的PSO算法、GA和SA算法的对比结果如表10所示。在可接受计算时间内，MILP模型能够找到本组11个算例中的9个最优解。对于未找到最优解的算例，模型所得解的质量也好于对比算法解的质量，如算例3。

4.6. 实验讨论与分析

通过本节实验发现，MILP模型能够在可接受计算时间内，求得总计37个算例中28个算例的最优解。与现有高性能的启发式[16]和元启发式算法[8,15]对比，所提模型能够获得质量更好的解。第4组和第5组实验是在广泛使用的著名数据集[21,29]上验证的，实验结果表明了所提模型的优越性。

如表11所示，所提模型包含了4种类型的下标，即工 序（operation）、机 器（machine）、OR节 点（OR node）和支路（link）；而文献[16]中的模型包含6种下标，即工艺特征（feature）、工序集合（operation set）、工序（operation）、机器（machine）、位序（position）和位置（place）。所提出的模型中较少的下标使得模型的求解比文献[16]中的模型更有效率。此外，基于OR节点的建模方法使得所提模型具有更强的通用性。这也解释了所提模型能够获得Kim [29]和Shin [21]数据集大部分最优解的原因。

表11 模型下标

5. 结论及未来工作展望

从工艺网络图的拓扑结构出发，本文为PP问题提出了一种基于OR节点的MILP数学模型。首先，提出了三种优先矩阵来讨论工序间的优先关系，然后引入了符号wjrl、url和xj来描述OR节点的选择机制以拓展模型的通用性，最后将模型编码并调用CPLEX求解器在公开数据集上进行验证。实验比较结果验证了所提模型的正确性和优越性。

本研究首次提出了基于OR节点的建模方法，为PP问题研究展示了新的思路。本文对三个优先矩阵的分析也揭示了工序排序子问题的本质，有利于进一步理解PP问题。然而，PP模型的相关研究仍存在一些局限性，即少数情况下无法找到最优解，且计算效率有时也不尽如人意。这意味着本文所提出的方法还可以进一步改进，模型的简化和加速方法是未来研究工作的重点之一。

致谢

本工作得到了国家自然科学基金（51825502、51775216）以及华中科技大学学术前沿青年团队计划（2017QYTD04）的支持。

Compliance with ethics guidelines

Qihao Liu, Xinyu Li, and Liang Gao declare that they have no conflict of interest or financial conflicts to disclose.