城市道路交叉口右转交通空间设计要素相关关系分析
2021-11-23吴昊江剑英谢林华
吴昊,江剑英,谢林华
(珠海市规划设计研究院,广东 珠海 519000)
长期以来,国内外学者对左转交通空间设计的研究非常重视,而忽视了右转。实际观察可见,在未设置右转专用相位情形下,信控交叉口右转车辆与行人和非机动车的冲突十分明显。其原因主要有:① 从相关法律法规来看,根据中国《道路交通管理条例》规定,右转车辆遇到红灯和黄灯时若不妨碍被放行车辆和行人的通行,可以通行。《道路交通安全法》规定,在获得通行权的相位里,人行横道上的行人其通行权高于机动车,但长期以来形成的“车不让人”的驾驶习惯很难在短时间内改变,可以预计右转机动车与行人之间的冲突仍将长期大量存在;② 右转交通的混合特征亦大大增加了交叉口右转机动车与非机动车交互的复杂性;③ 从右转车辆微观交通运行特征来看,右转车流在交叉口处于两种状态,一种是减速右转,另一种是启动右转,均会与分、汇流车流产生较大的速度差,显著增加车辆之间产生交通冲突的概率。
为此,该文通过分析右转车流与交叉口渠化、其他交通参与者之间的关系,及其对交叉口通行能力的影响和交通冲突产生机制进行归纳总结,并以实地调研的方式,使用描述性统计方法、方差分析以及多元回归分析法,对右转交通设计要素之间的耦合作用进行系统分析,探索交叉口右转弯车速与各影响因素之间的数量依存关系,为城市道路交叉口的规划、改造及精细化设计提供科学的依据。
1 右转交通运行状况影响因素
在城市规划设计体系中,交通设计承接和协调城市和交通规划,指导交通基础设施建设(图1)。宏观的城市交通规划侧重于根据城市发展需求从整体上把握交通设施网络的布局,精细化交通设计则是系统性地解决中微观层面交通问题的重要手段。精细化交通设计要求统筹交通环境各类设计要素,从交通的实际参与者角度出发,平等地考虑交通的各类参与者。
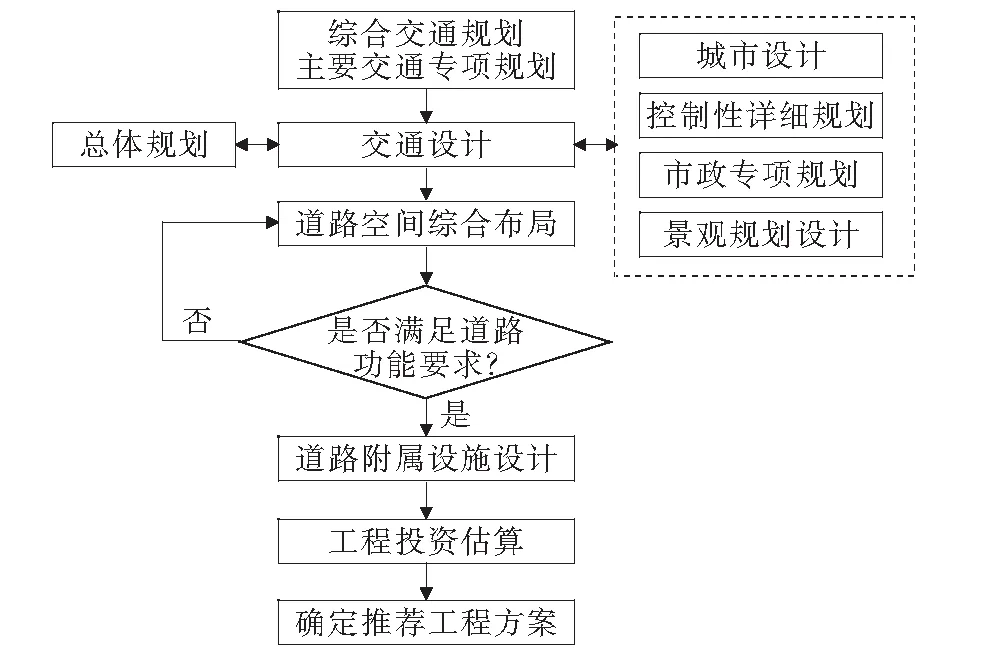
图1 城市道路系统规划设计流程简图
城市道路交叉口右转交通环境中各要素的交互具有较高的复杂性,而交通空间设计权衡的关键是通行能力和交通冲突,下文对右转交通空间设计与交叉口通行能力之间的耦合关系以及交通冲突的产生机制、影响因素等进行简要的归纳总结。
1.1 通行能力
美国通行能力手册(HCM)中将右转车对车道组饱和流率的影响以车道组基本饱和流率与右转车校正系数相乘的形式表达,加拿大《信号控制交叉口通行能力导则(第3版)》修正系数包括:左右转弯半径、停车、行人影响、绿灯时长、左右转专用车道等,其中转弯半径对饱和流量的影响直接用修正系数来表达,以转弯半径基准值为15 m,小于15 m时进行修正。
目前应用比较广泛的是CJJ 37—90《城市道路设计规范》给出的方法,该方法根据直行车道通行能力、有无右转车道以及转向车辆比例等确定交叉口通行能力;而停车线法中右转车道通行能力的计算考虑车型比例以及有无过街行人等因素的影响;冲突点法在计算交叉口通行能力的过程中加计右转专用车道的右转车实际到达数。有学者对右转弯半径与饱和流率之间的相关性进行分析,结果表明右转弯半径与饱和流率之间存在明显正相关。文献[7]探究右转弯速度与转弯半径之间的关系,结果表明二者存在正相关关系。
1.2 交通安全
不同流向交通流之间的相互干扰产生冲突,交通冲突未经妥善处理就会转化为交通事故,蒙纳斯大学事故研究中心、英国交通研究实验室以及部分学者对车速以及车速离散性与交通事故之间的关系进行了研究,结果表明平均车速与车速之间的差值越大,则交通流运行越不稳定,事故率越高。
文献[10]考虑交通流接受间隙以及车辆跟驰行为,并建立右转机动车穿越非机动车的微观行为模型,以揭示右转机动车与非机动车的干扰机理;文献[11]研究发现非机动车面对小型车进行“加速超车”的可能性是面对大型车时的2倍,由此可见,右转机动车的车型亦对冲突交通流的行为表现有影响,不同车型对右转弯线形提出不同要求,中国城市典型信号交叉口设计中,在有右转专用道的情况下通常存在两种渠化方式(图2),分别是划线渠化道和实体渠化道,两种渠化设计方式在机动车通行效率、行人过街安全以及土地利用等方面各有利弊,最大的不同在于对行人过街的处理。有研究表明:行人在结伴通行或者专用右转进口道且在行人绿灯初期过街等情形下发生冲突的可能性更大。

图2 两种常见的右转渠化方式及机非人冲突示意图
也有学者结合工效学的相关概念进行研究,结果表明:车速以及驾驶员盲区是导致交通冲突和事故的两个主要原因。影响车辆转弯轨迹的主要因素包括交叉口几何条件、车辆及驾驶员自身因素,以及其他交通参与者的干扰等。
由此可见,右转交通的运行状况不仅与交通参与者及其微观行为有关,而且受交叉口渠化方式、信控模式等因素的影响。从通行效率以及交通安全性两个角度出发,右转交通设计中往往需要仔细考量右转弯速度,以及右转弯速度与转弯半径、人非参与者等影响因素之间的关系。为实现交叉口交通系统高效率高安全性运行的目标,需要同时考虑的影响因素包括转弯空间以及参与主体,而转弯空间规划设计具有更强的可操作性,如转弯线形等。
2 右转弯线形确定方法综述
实际的右转交通规划设计工作的局限性在于未平等考虑右转交通环境中的各类参与者,且处于定性考量阶段而无可靠的定量依据作为支撑。该节以右转弯线形之转弯半径的确定方法为例对其存在的问题进行分析,并对右转弯线形国内外相关规范规定进行简要归纳。
2.1 路缘石转弯半径建模方法
CJJ 37—2012《城市道路工程设计规范》中要求道路交叉口设计应符合现行行业标准CJJ 152—2010《城市道路交叉口设计规程》的规定,CJJ 152—2010中规定了路缘石转弯半径的确定方法,计算公式为:R=V2/127(μ+i)。其中:R为路缘石转弯半径(m);V为道路设计速度(km/h);μ为横向力系数;i为路面横坡度。该模型的建立考虑的是转弯空间要素,忽略了车型以及道路等级适应性。
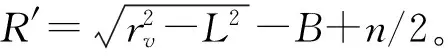
2.2 各国关于右转弯线形的规定
(1)美国:根据车辆车速≤15 km/h时的转弯轨迹确定最小转弯半径,提供了与不同转弯角度、车型等相对应的最小转弯半径,针对不同类型公路提出了推荐的转弯半径,曲线半径取9 m可满足小客车转弯要求。
(2)中国:JTG D20—2017《公路路线设计规范》中规定鞍式列车在不同转弯速度条件下的路面内缘最小半径,非渠化平面交叉口转弯空间设计主要考虑载重汽车,转弯路面内缘圆曲线半径可取15 m。
(3)德国:明确提出9类右转弯线形以及选取转弯线形时应考虑的因素,并对常规和受限条件下不同等级道路可选用的转弯曲线类型进行规定。
(4)日本:针对各类型设计车辆给出转弯半径范围。
(5)英国:规定转弯半径、渐变率以及渐变段长度,交叉口最小半径取10 m。
以城市道路交叉口的右转交通空间为研究对象,对右转交通环境各要素之间的相互影响进行归纳总结,具体体现为右转交通流对交叉口通行能力和交通安全性的影响,并归纳总结右转弯半径的确定方法以及各国对右转弯线形设计的相关规定,从而得出右转交通的主要影响因素类型包括转弯空间和参与主体。
3 右转交通空间设计要素相关关系分析
3.1 试验设计
右转交通环境各要素之间相互作用的逻辑可以表达为:各因素对右转机动车交通流的影响通过右转弯车速较为直观地体现出来,而车速又进一步影响交叉口通行能力和交通安全性。该文选取弯道几何特征、渠化特征、离开道路特征等作为右转弯车速的影响因素进行调查研究,具体如表1所示。

表1 右转车速影响因素

3.2 结果分析
3.2.1 数据基本特征分析
研究共计采集数据1 143条,首先利用SPSS24.0软件对采集的有效数据进行初步的描述性统计分析。变量中右转弯半径和右转弯车速均为计量资料,描述性统计值如表2所示,其中右转弯半径平均值为16.811 m,右转车速平均值为18.89 km/h。

表2 数据集描述性统计表
由图3可以较为直观地观察到右转弯速度大小的分布情况,进一步根据描述性统计结果中显示,右转弯速度记录数据偏度、峰度系数均小于1,且K-S检验结果中显著性水平P值大于0.05,可知右转弯速度记录数据呈近似正态分布。

图3 右转弯速度频数统计直方图
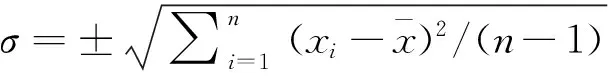
对原始数据剔除异常数据16条,采纳有效数据1 127条(表2)。
3.2.2 不同因素水平下右转弯车速差异对比
研究的观测变量为8个,各个观测变量有1 127个有效观测数据,具有多变量大样本之特点,因此需要进行因子分析以检验变量之间的关系假设,其基本原理为找出各观测变量均包含的共性因子。
利用SPSS24.0软件对所得数据集进行因子分析(图4),根据KMO统计量为0.471,小于0.5,以及碎石图(图4)中各因子之间特征值差异较大可得,各因子之间并无统计学意义上的显著相关性,即从本质上来讲各变量之间不存在潜在的共性因子,因此认为该文对于右转弯车速的影响因素分类较为合理。
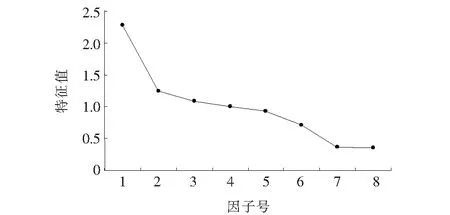
图4 因子特征值差异
在确保各因子之间相互独立的基础上,为了深入分析不同水平因素是否会对右转弯车速产生显著影响,即对比不同因素水平下的右转车速均值是否有显著差异,该文采用单因素方差分析法进行均值对比,单因素方差分析统计汇总如表3所示。
由表3可得:有无右转专用道两种情形下右转弯车速均值有显著差异,F统计值为104.935,显著性水平P小于0.05;进入道路有无路内停车两种情形下右转弯车速均值有显著差异,F统计值为79.815,显著性水平P小于0.05;离开道路有无路内停车两种情形下右转弯车速均值有显著差异,F统计值为35.657,显著性水平P小于0.05;车型在不同水平下右转弯车速均值有显著差异,F统计值为1.190,显著性水平P小于0.05;有无人行过街两种情形下右转弯车速均值有显著差异,F统计值为95.840,显著性水平P小于0.05。

表3 ANOVA统计汇总
由表3中显著性水平P值小于0.05可得,不同进入道路设计车速水平下的右转车速具有统计学意义上的差异。在进行事后检验的过程中,进入道路设计车速水平被分为5组,分别为[20,25]、[25,30]、[40,45,55]、[45,50,55]、[60],可见,并非进入道路设计车速各水平下两两右转车速均值之间均有显著差异。离开道路设计车速水平被分为4组,分别为[20]、[25,30]、[30,40,45,50]、[40,45,50,55,60],可见,并非离开道路设计车速各水平下两两右转车速均值之间均有显著差异。
3.2.3 右转弯车速影响因素多元线性回归分析
在对右转弯车速影响因素的各自作用进行一一剖析的基础上,为了构建右转弯车速及其影响因素之间的数量依存关系,该文在对调查数据进行描述性统计和不同因素水平下右转弯车速均值差异对比的基础上,进一步对因变量(右转弯车速)与自变量(右转弯半径、进入道路设计车速以及车型等)之间的关系进行多元线性回归分析。
由于在处理实际问题时,人们总是希望选择一些对因变量有显著影响的变量作为自变量,以便进行预测和分析,而步进法就是依据这一原则提出的回归分析方法。该文利用步进法对右转弯车速及其影响因素进行回归建模,表4为步进法对变量进行输入的过程中模型拟合程度指标值R的变化过程,表5为多元线性回归模型中各因素系数统计。
根据模型方差分析统计检验结果中显著性水平P值小于0.05表明,所构建的回归模型具有统计学意义。表4为各步模型汇总情况。从表4可以看出:多元线性步进回归分析模型的相关系数R为0.726<0.789<0.829<0.838<0.845<0.850,说明第6步的因变量与自变量之间的相关性最佳;结合德宾-沃森检验及前述因子分析结果,认为符合线性回归独立性条件,即忽略自变量个数对R2的影响;根据第6步调整后R2=0.721可得,右转弯半径、有无人行过街、进入道路设计车速、离开道路有无路内停车、车型、进入道路有无路内停车等变量对右转弯车速的解释率为72.1%;而右转弯半径、有无人行过街、进入道路设计车速对右转弯车速的解释率为68.4%。
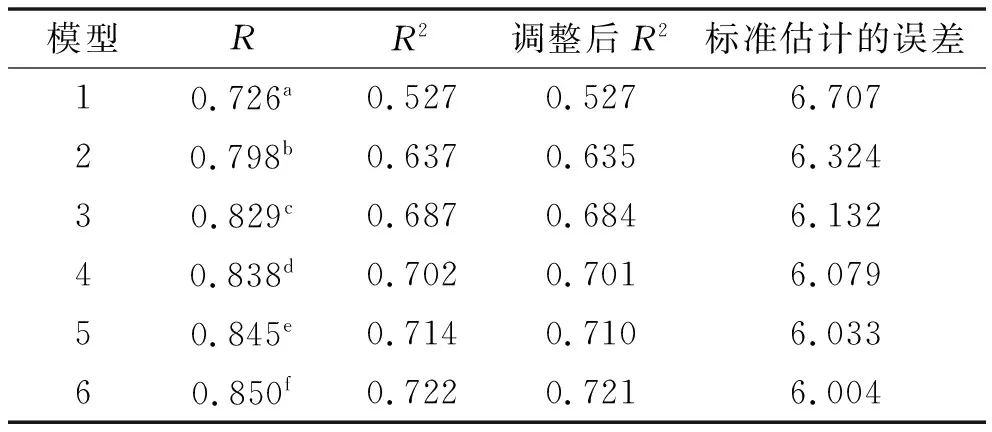
表4 步进法模型拟合程度指标值汇总
表5为第6步模型的多元线性回归系数。常数项(常量)系数b0=13.044,b1=0.274,b2=-9.358,b3=0.125,b4=-2.821,b5=-2.340,b6=-1.949。通过t检验,常量以及各个因子回归系数的相伴概率值均小于因子剔除标准值0.1,进一步证明模型具有统计学意义。而根据标准化系数的绝对值可以得出右转弯半径对右转弯车速的影响程度最大,有无人行过街对右转弯车速的影响程度次之,进入道路设计车速对右转弯车速的影响程度亦较高。
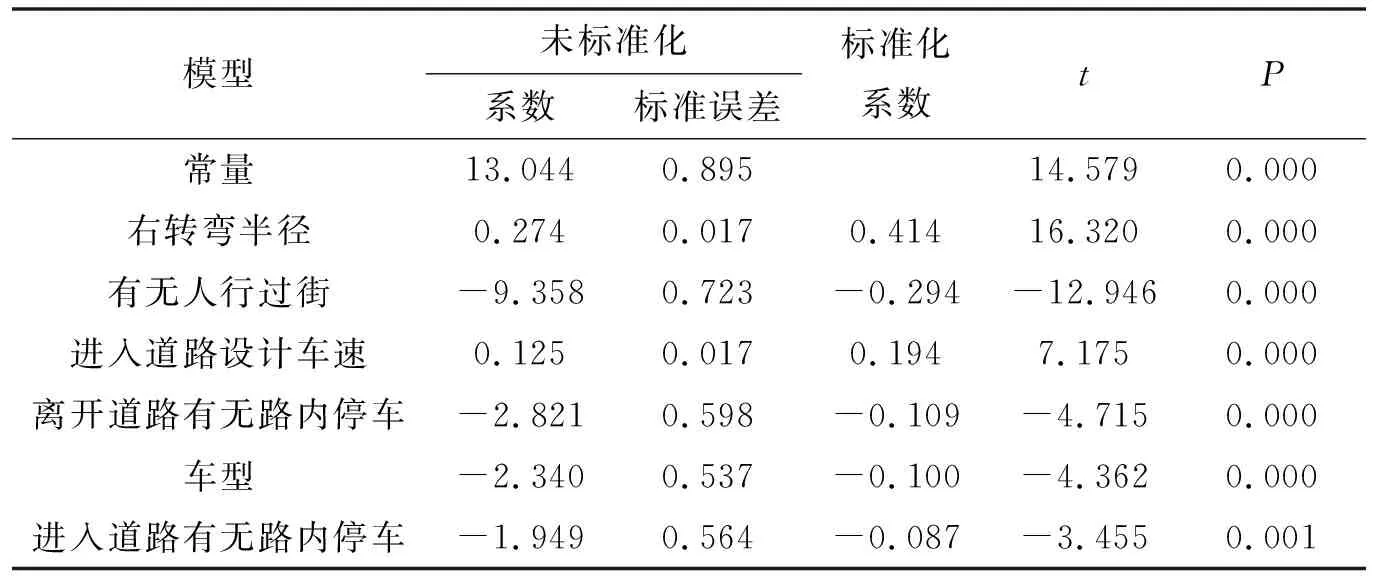
表5 多元线性回归系数
综上,转弯空间以及参与主体各因素均对右转车速产生显著影响;右转弯半径、有无人行过街、进入道路设计车速、离开道路有无路内停车、车型、进入道路有无路内停车等变量对右转弯车速的解释率为72.1%;而右转弯半径、有无人行过街、进入道路设计车速对右转弯车速的解释率为68.4%。
4 结论
城市道路平面交叉口设计中,右转弯空间设计主要结合道路的等级、功能定位、通行车辆类型进行灵活选取。无定量参考依据的情况下,设计人员无法验算工程实施后的实际通行效果,该文的研究成果实际上主要可以提供两点参考依据:
(1)根据“右转弯半径、有无人行过街、进入道路设计车速可以解释右转弯车速68.4%的变差”这一研究结论,可得右转交通空间设计应着重考虑右转弯半径、行人过街渠化以及进入道路的设计车速。
(2)在确定转弯空间各设计要素后,验算不同车型及有无人行过街情形下的右转交通实际通行效果。
