截面不均匀收缩对T梁腹板受力性能影响分析

2021-11-23周静雯何舒法王龙黄乐州

中外公路 2021年5期

周静雯，何舒法，王龙，黄乐州

(长安大学公路学院，陕西西安 710000)

混凝土收缩是混凝土材料自身特性之一，随着时间推移，混凝土收缩应变不断发展，混凝土收缩可使结构内部产生微裂缝，收缩发展速度较快，导致结构产生不均匀变形，甚至导致局部应力超限，使结构开裂；对于预应力结构，混凝土收缩将直接导致预应力损失；此外，混凝土收缩是导致结构内力重分布及长期变形的重要因素之一。

多年来国内外大量专家学者对混凝土收缩机理及预测展开了大量的研究，也取得大量研究成果，但混凝土材料自身的复杂性使得混凝土收缩的预测较为困难，现在常用的预测模型都为根据试验数据拟合的经验公式，每种预测模型的侧重点也不尽相同，各种混凝土收缩预测模型均需结合实际结构进行选取并加以验证。对于各种收缩预测模型，构件的理论厚度是描述混凝土收缩的一个重要参数，构件理论厚度对构件收缩应变发展速率有相当明显的影响。工程中一般认为结构只产生体积收缩变形来近似考虑收缩对结构的影响，根据文献[1]、[3]、[4]可知，由于构件各部位收缩变形发展不同步，构件产生较明显的截面非均匀收缩现象，导致结构构件不仅产生轴向收缩效应，同时产生挠曲变形。

预应力混凝土T梁桥是公路建设过程中常用桥型之一，通过T梁的预制、安装、整体化等过程成桥。近年来，随着T梁桥的大规模建设，部分该类结构典型病害也日益凸显。其中，T梁腹板竖向裂缝由于产生频繁，开裂机理不明确，重新引起大量学者的关注。大部分研究针对T梁桥施工原因分析，通过阐述潜在开裂因素，提出相应的处置对策，却并未量化各种因素对结构的影响，无法形成相应的理论体系指导实际开裂问题处治。根据裂缝的形态特征，以及裂缝产生的时间，部分学者对T梁桥的收缩、徐变性能进行了进一步的探讨，由于T梁截面厚度与配筋的变化，截面非均匀收缩、徐变对结构受力性能产生一定的影响，并提出相应的理论推导。但在计算过程中，对潜在影响因素考虑不尽充分。

该文针对预应力混凝土T梁桥考虑各部分理论厚度(或比表面积)不同、考虑桥面铺装的影响、考虑普通钢筋作用的影响下截面产生的不均匀收缩效应进行研究。通过选择合理收缩预测模型，计算相应各部位理论构件厚度，建立ADINA实体有限元模型对T梁不均匀收缩规律进行精细化分析。

1 混凝土收缩计算及截面不均匀收缩效应

1.1 混凝土收缩计算

目前，各混凝土收缩预测模型中，结构构件理论厚度(比表面积)是影响混凝土构件收缩应变发展的重要参数，通常对混凝土收缩效应，往往以杆系理论为基础进行计算，认为梁体为整个构件，通过计算整片梁板的理论厚度进行均匀收缩应变的考虑。常用的收缩预测模型有：

(1)CEB-FIP 1990

εs(t,ts)=εs0β(t-ts)

(1)

式中：εs(t,ts)为t时刻混凝土自收缩应变；εs0为收缩终极应变；β(t-ts)为随时间发展函数。

(2)ACI 209R-1992

(2)

式中：εs,∞为收缩终极应变；f为混凝土抗压强度。

(3)GL 2000

εs(t,ts)=εs,∞β(RH)β(t-ts)

(3)

式中：β(RH)为环境湿度影响系数。

3个预测模型函数形式相同，由于不同模型采用的数据、评判的标准、考虑的因素不同，对混凝土收缩预测的结果均有相当大的差异。国内外学者对混凝土收缩徐变模型做了大量的对比分析，一般认为：CEB-FIP 1990对混凝土收缩预测值偏低，ACI对混凝土收缩预测值与其他模型趋势存在较大差异。综合而言，GL 2000模型计算结果更适用，使用范围更广，且计算公式更为简单通用。

此外，对于早期混凝土，非线性湿度扩散理论也常用于混凝土收缩变形分析中，求解三维非线性对流扩散问题，是求解三维非线性对流扩散方程的初边值问题，可采用数值计算方法。由于计算过程中所需参数较多，该文取前者收缩预测理论。

实际结构在养护与使用过程中，不同部位与大气接触面积、厚度、配筋率等都不相同，加之施工过程中不可避免的质量问题，故梁体不同部位收缩发展规律存在一定的差异。该文以单梁自收缩、考虑桥面铺装自收缩、考虑普通钢筋自收缩3种不均匀收缩效应进行分析。

1.2 结构构件理论厚度(比表面积)

(1)一般截面构件理论厚度(比表面积)

由于T梁结构腹板与顶板两个维度尺寸远大于另一个维度尺寸，计算时以板特性进行考虑，认为其体表比接近构件厚度的一半，即V/S≈h/2，其余部位体表比以V/S进行考虑。T梁截面变化过程采用线性内插过度，构件理论厚度(比表面积)特性如图1、表1所示。图中：A-A为T梁支点截面，B-B为T梁变截面处，C-C为T梁跨中截面。

图1 不同 T梁截面体表比

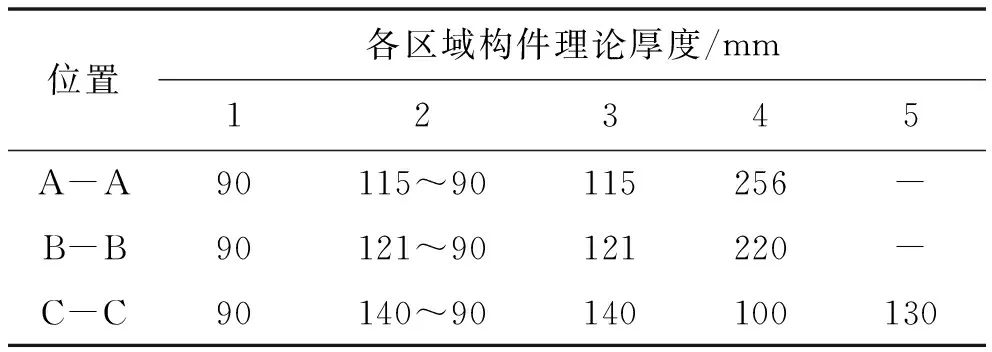
表1 不同位置理论厚度(比表面积值)

图2为T梁不同部位随时间产生的收缩应变。由图2可知：按截面不同部位考虑混凝土收缩特性在截面内部将产生相当大的收缩应变差，不同收缩模型所得结果存在一定差异。其中T梁腹板与上下部位不同预测模型最大应变差分别为：1.93×10-4(A-A截面)、1.68×10-4(B-B截面)、6.5×10-5(C-C截面)。

图2 收缩应变曲线

(2)考虑桥面铺装对结构的影响

T梁在预制架设过程中，不同梁体存梁时间存在差异，桥面铺装完成时间存在差异，均对桥梁内部产生一定量的应变差。实际桥梁在干燥环境中，应考虑桥面铺装的影响，桥面铺装由10 cmC50混凝土和10 cm沥青混凝土组成。

若考虑桥面铺装等效应影响，顶板比表面积相应增大，但桥面现浇混凝土较薄，收缩发展较快，桥面铺装对结构收缩效应的影响较难准确估计。在该文计算过程中，对于较不利工况的计算将计入10 cm现浇混凝土层对顶板厚度的影响。不考虑沥青混凝土对结构收缩性能的影响，假定现浇桥面板上侧与空气接触，假定区域1、2、3在浇筑桥面板后，比表面积(理论厚度)分别以最不利190～140、140 mm计入。

2 截面不均匀收缩效应分析

2.1 有限元模型建立

通过ADINA建立3D实体有限元模型，普通钢筋(包括结构纵向受力钢筋、架立钢筋、箍筋、防崩钢筋)采用Rebar方式进行考虑，对T梁收缩效应进行分析。计算过程中，取单片T梁进行分析，通过GL 2000收缩模型计算得到的收缩应变随时间变化曲线，以升、降温的方式考虑T梁结构收缩效应。根据式(4)可计算得出与混凝土收缩应变相对应的温度值。

(4)

式中：ε为收缩应变；T为收缩应变等效温度(℃)；α为混凝土热膨胀系数，取1×10-5(1/℃)。

2.2 截面不均匀收缩效应

根据结构各部位比表面积可知，不同部位收缩应变发展速率不同。以跨中截面为例，不考虑桥面铺装时，桥梁顶板与腹板比表面积接近，马蹄部位比表面积较大，腹板与顶板收缩速率高于马蹄部位；考虑桥面铺装时，腹板比表面积明显小于顶板和马蹄，则腹板收缩速率发展较快。

此外，普通钢筋与构造钢筋可有效分布混凝土收缩及温度产生的应力，对防止结构非结构性开裂，提高结构耐久性有着重要作用。普通钢筋对混凝土自收缩效应有着约束作用，会阻碍混凝土收缩的发展，根据30 mT梁上部构造通用图可知，顶板、腹板、马蹄配筋率分别为0.92%、0.28%、3.23%，不同的配筋率对各部位混凝土的收缩发展速率也将存在较明显的影响。

通过分析T梁自收缩效应，并引入桥面铺装及普通钢筋的影响。以数值计算方法，得出不均匀收缩对结构的影响。以考虑桥面铺装时T梁不均匀收缩正应力分布规律为例(图3、4)，其余各工况收缩效应与该工况收缩效应应力值有差异，但分布规律相似，不再列出。

图3 730 d梁体收缩正应力图(单位：MPa)

图4 C-C截面T梁非均匀收缩正应力(单位：MPa)

由图3、4可知：由于腹板比表面较小，收缩发展较快，腹板以拉应力为主，顶板与马蹄比表面积较大，收缩发展较慢，以受压为主。由于同类混凝土收缩应变终极值相同，T梁各部位间收缩应力差主要由于收缩速率不同而产生，总体呈先增长后减小的趋势。自收缩应力差峰值出现在2～5年，后期随着时间的推移，该应力差值逐渐减小。

该文中不考虑普通钢筋与混凝土之间的黏结滑移。由计算可得普通钢筋由于混凝土收缩产生的最大压应力位于T梁腹板箍筋处，在730 d左右时，普通钢筋压应力计算值达到60 MPa，随着时间的增长，钢筋应力不断增长，3 650 d时达到90 MPa。由于马蹄部位配筋率大于腹板及顶板，对截面刚度影响较大，对梁体收缩约束作用明显。计算时考虑钢筋作用，对T梁马蹄与腹板交接位置及腹板中部应力影响较大。

图5为不同工况T梁腹板自收缩应力差随时间的变化。

图5 不同工况T梁腹板自收缩应力差随时间的变化

由图5可知：各部位比表面积不同对腹板应力分布规律有较大的影响。当时间达2年左右时，腹板拉应力趋近于峰值。顶、腹板交接处应力峰值为0.6 MPa(裸梁自收缩)、1.0 MPa(考虑普通钢筋)、2.2 MPa(考虑桥面铺装)；马蹄、腹板交接处应力峰值为1.1 MPa(裸梁自收缩)、2.3 MPa(考虑普通钢筋)、1.2 MPa(考虑桥面铺装)。当同时考虑普通钢筋与桥面铺装作用时，T梁腹板平均拉应力达到2.3 MPa，收缩应力影响量值已不可忽视。