基于极限承载与局部破坏冗余度的桥梁优化设计

缪卫清，宋华，常军

(1.苏州科技大学 土木工程学院，江苏 苏州 215011；2.上海沪中建设工程造价咨询有限公司)

1 引言

冗余度是为避免结构体系连续倒塌而用多余构件将结构由静定结构变成超静定结构的设计。在判断结构体系的几何可变性时，超静定次数通常被视为其冗余度。在评估构件和结构的安全性时，极限承载能力大于所需承载能力要求的部分被视为冗余度。

尹德兰等通过分析几个破坏的桥梁在几种初始损伤发生后的反应引入了桥梁体系设计冗余度的概念；Yun,Hyojeong等采用数值模拟方法研究了钢结构多梁桥损伤后的冗余度，结果表明钢工字梁桥在降低材料强度和下翼缘数量后具有足够冗余度；叶华文等分析了魁北克大桥有限元模型的冗余度和失效模式，结果表明该桥是无冗余度的静定结构，部分构件因外力失效而导致结构整体失效。冗余度不仅可以用于评估结构整体性，还可用于寻找到结构中的关键构件或影响结构的重要因素。C.Tony Hunley等通过分析双筒形钢梁桥的冗余度，确定了不同桥梁构件在损伤梁向未损伤梁的荷载传递过程中的作用；Janghwan Kim等分析了某双钢箱梁桥一根梁因车辆活载突然断裂的现象，结果表明螺栓连接失效对钢箱梁桥的冗余度影响较大；Lin W等采用数值模拟方法分析了某三跨双工字梁桥的断裂冗余度及断裂后的承载能力，结果表明混凝土板是保证双梁钢-混凝土组合桥梁冗余度的重要构件；朱南海等以敏感性为冗余度指标分析了3个缩尺后的网壳模型，找到了破坏后对结构影响最大的关键构件；蒋淑慧等基于冗余度理论提出定量评估铰接杆系结构体系中各杆件重要性的方法。在定义了结构冗余度的分布系数后通过分析拆除不同杆件后剩余结构体系冗余度的分布系数量化各杆件在结构体系中的重要性；朱劲松等通过分析某中承式系杆拱桥的冗余度得到不同种类的局部破坏形式对桥梁体系承载能力以及正常运行的影响；夏建中等分析了某基坑拆除部分构件后剩余结构体系的冗余度，结果表明最下道支撑失效后对结构体系的影响很大，施工中应重视该构件并采取相关措施；郑刚等分析了不同平面布置的环梁水平支撑结构体系局部杆件破坏后的冗余度，找出重要构件并进行优化设计，同时在施工中重点监测、保护；吴星煌将大型网壳结构在局部构件破坏后的整体性能定义为其结构冗余度，反映了各构件在结构体系中的重要性。

冗余度还可用于量化损伤后结构的性能：Park YM等评估了某单跨两板梁桥在其中一根主梁严重破坏后的冗余度。结果表明横梁和混凝土桥面在一定程度上重新分配了作用于未开裂梁的荷载，侧向支撑体系在梁受损伤时对荷载的重新分配起着重要作用。Hun Cha等通过现场控制断裂试验评估了某全尺寸桁架桥结构的冗余度，对该桥的断裂后行为和冗余度进行了量化。

目前，由于多方面的原因导致车流量越来越大，超重车越来越多，进而导致桥梁局部破坏和超载运行。为了保证桥梁在超载运行和局部破坏情况下仍有一定的承载能力，需要对基于现行规范桥梁设计进行优化。该文通过采用极限承载冗余度和局部破坏冗余度对桥梁结构在超载及局部破坏时的承载能力进行量化，进而优化桥梁设计。

2 基本原理

定义结构的承载能力储备系数Ru和局部破坏储备系数Rd如下：

(1)

(2)

式中:LF1为完好结构发生第一个构件破坏的荷载系数；LFu为完好结构达到承载能力极限状态的荷载系数；LFd为已发生某一构件破坏的结构达到承载能力极限状态的荷载系数。

定义评估桥梁结构在超载运行时承载能力极限承载冗余度ru和在局部破坏后承载能力局部破坏冗余度rd如式(3)、(4)：

(3)

(4)

若ru≥1，则桥梁在超载时的承载能力有足够的冗余度，若桥梁中某个构件失效后剩余体系的rd≥1，则体系对该局部破坏有足够的冗余度。

3 算例分析

建立如图1所示的简易桁架桥模型，每跨长3 m，共6跨，桥梁高度3 m。构件编号见图1。工况荷载如图2所示。

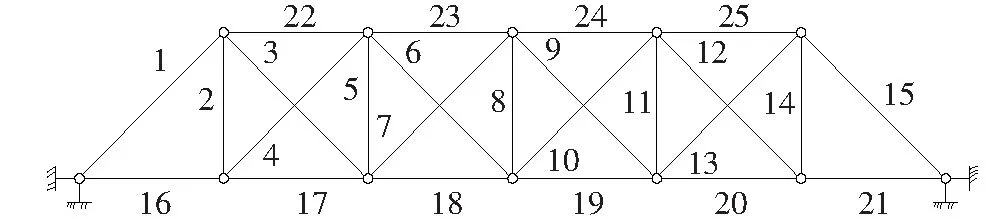
图1 桥梁模型及构件编号

杆件16～21号模拟桥梁上部结构桥面系统的主梁结构。1～15号杆件模拟剩余的上部结构杆件，在桥梁使用过程中易发生初始损伤，退出工作。桁架结构的设计使用荷载如图2所示。在桥梁的使用期间偶尔会有超载运行。

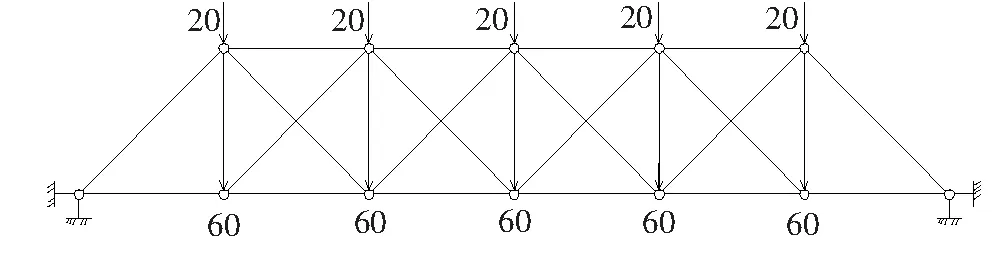
图2 桥梁作用的荷载(单位：kN)

根据既定荷载计算得出各杆件所受轴力如表1所示(由于结构对称，只列出一半构件，下同)。

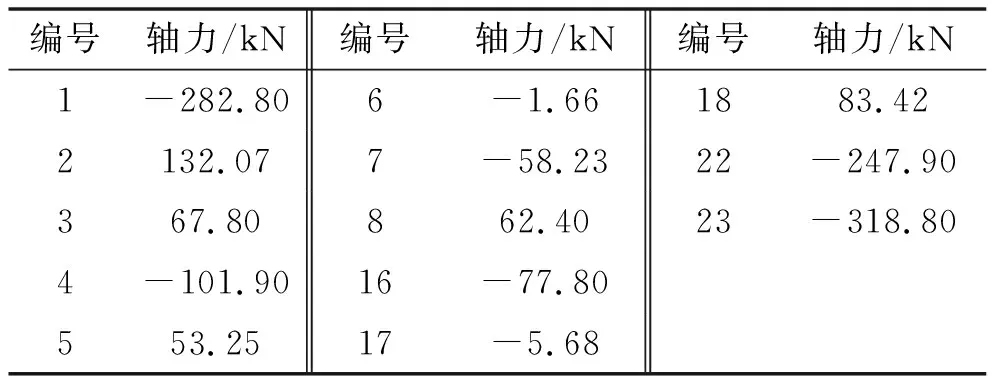
表1 各杆件所受轴力

桁架结构中的杆件在承载时只受轴力，当所受压力达到一定数值会发生弯曲变形，随后因失稳而破坏退出工作。因此，用稳定系数考虑各杆件因弯曲变形引起的破坏。由计算所得杆件轴力初步设计各杆件截面尺寸以及相关材料参数详见表2。

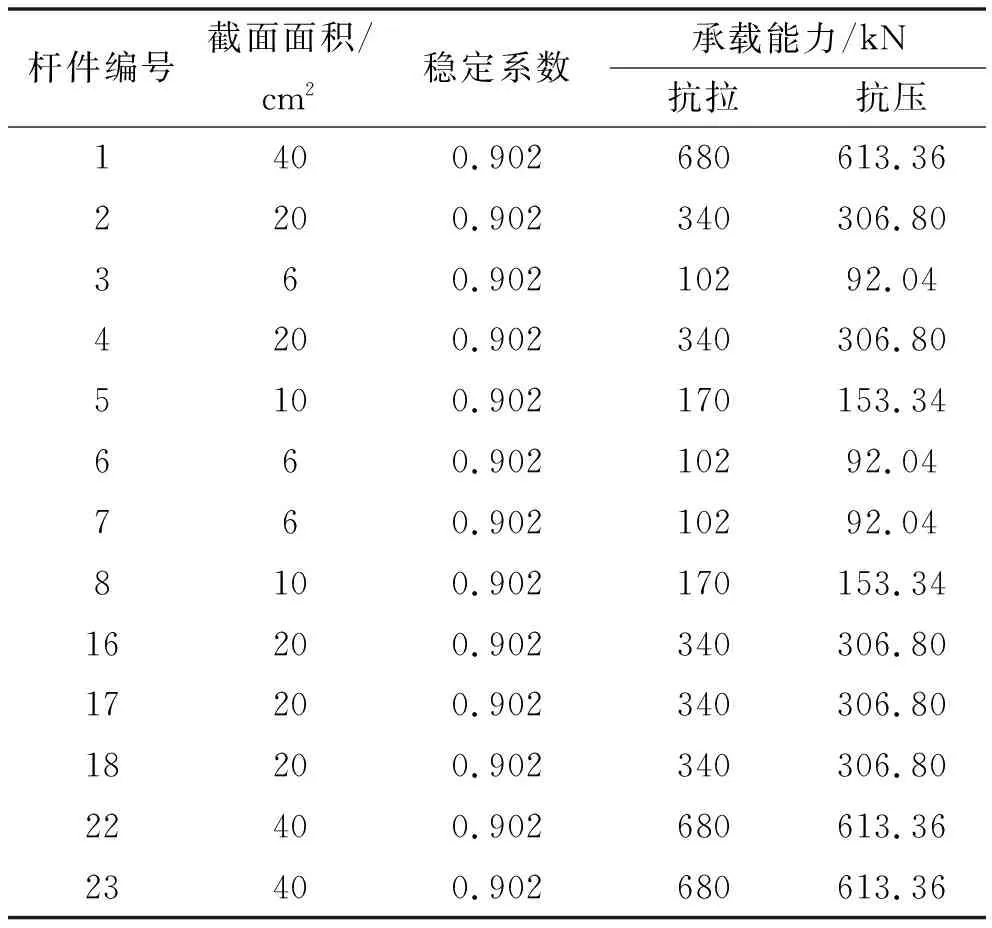
表2 设计截面尺寸及材料参数

分析初始设计下桁架结构的极限承载冗余度和8种局部破坏冗余度。定义荷载系数为工况荷载的倍数。先求LF1和LFu。当荷载系数为1.505时,3、13号杆件计算轴力达到102.010 6 kN，超过极限承载能力，杆件破坏退出工作。剩余结构体系受力如图3所示，荷载再分配如表3所示。

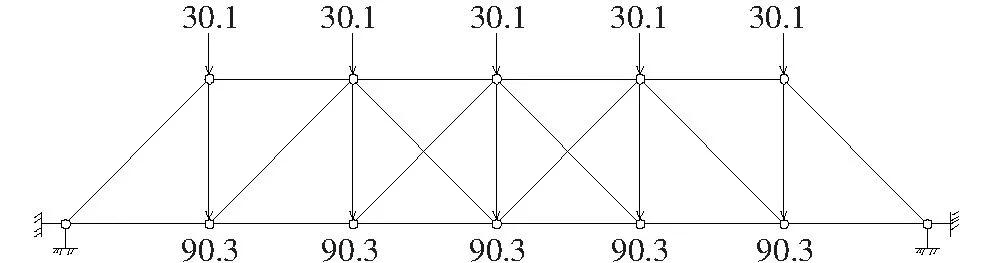
图3 3、13号杆件失效后剩余结构受力图(单位：kN)

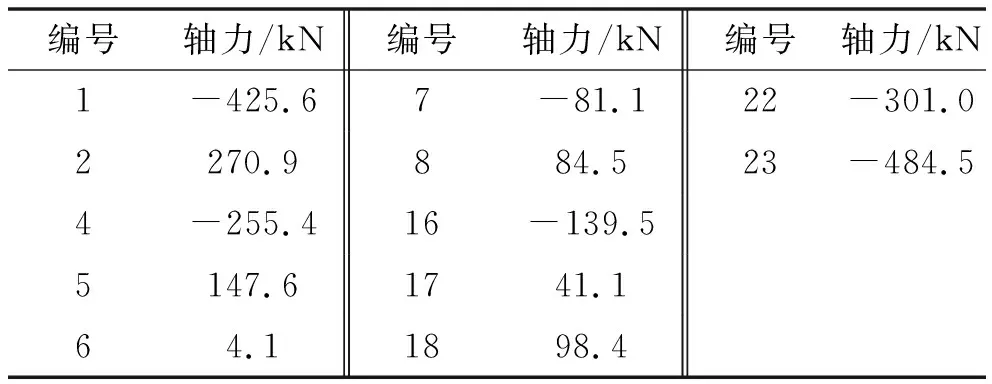
表3 3、13号杆件失效后荷载再分配

荷载再分配后7、9号杆件轴力达到-81.05 kN,已至承载极限的88%。当荷载系数为1.709 1时，7、9号杆件计算轴力达到-92.04 kN，超过极限承载能力，杆件破坏退出工作。7、9号杆件破坏退出工作后剩余杆件计算轴力如表4所示。

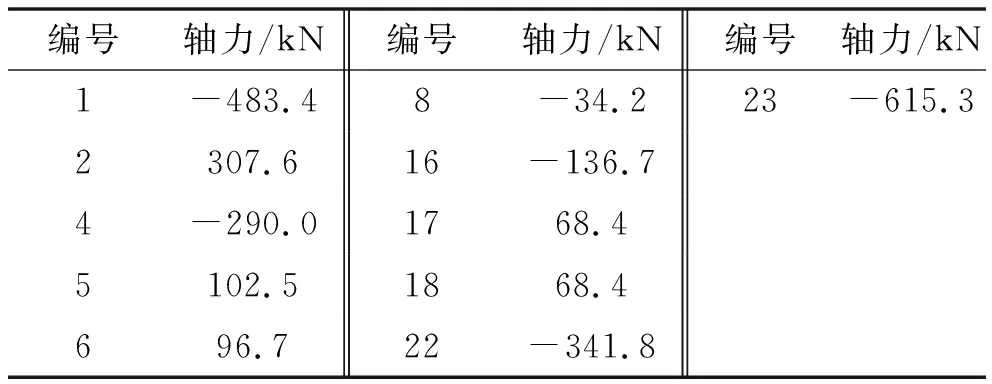
表4 3、13、7、9号杆件失效后各杆件计算轴力

7、9号杆件也失效后，23、24号杆件计算轴力都超过极限承载能力，结构体系整体破坏。因此初始设计时LFu=1.7091，LF1=1.505。由式(1)、(3)计算得到ru=0.87<1。

接着分析结构体系易发生的8种局部破坏，即1～8号杆件失效后继续承载的能力。9～15号杆件与1～8号杆件对称，局部破坏情况与1～8号杆件相同。

1号杆件失效后桁架称为瞬变体系，视为结构整体破坏。即LFd1=0，rd1=0。

2号杆件失效后剩余结构受力如图4所示，荷载再分配如表5所示。

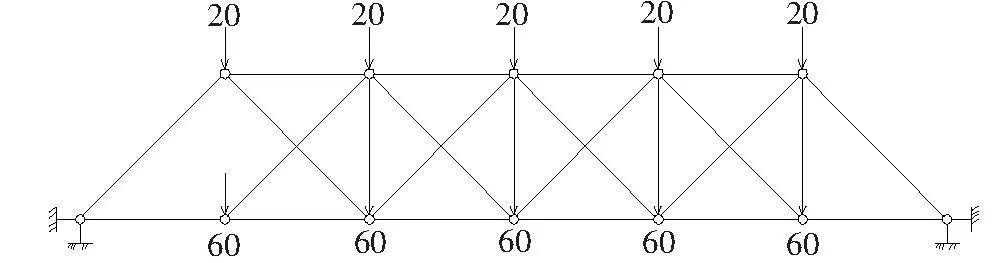
图4 2号杆件失效后剩余结构受力图(单位：kN)

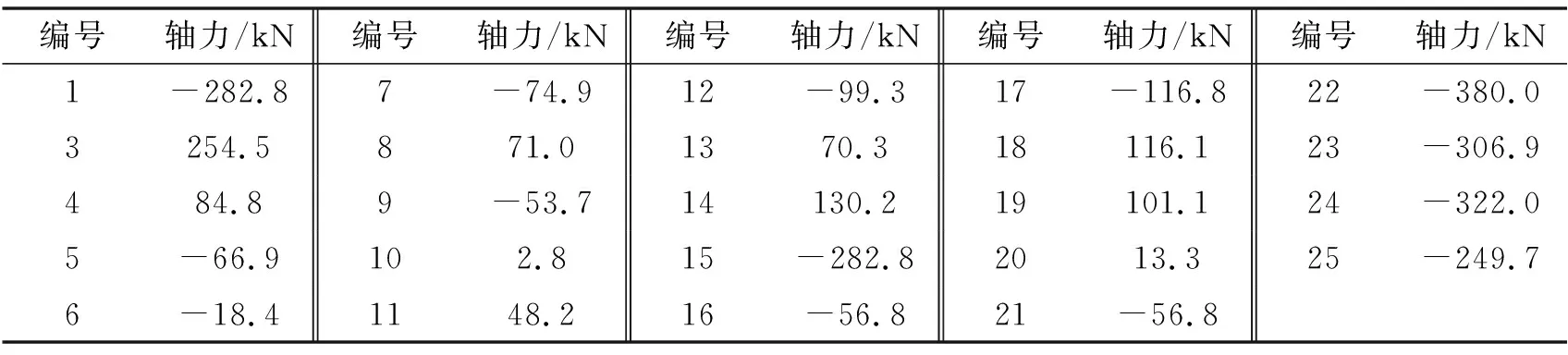
表5 2号杆件失效后各杆件计算轴力

3号杆件计算轴力达到254.5 kN，超过自身极限承载力。3号杆件也失效后结构体系成为瞬变体系，视为结构整体破坏。因此，LFd2=0，rd2=0。失效路径为杆件2→杆件3。

3号杆件失效后剩余结构荷载再分配见表6。

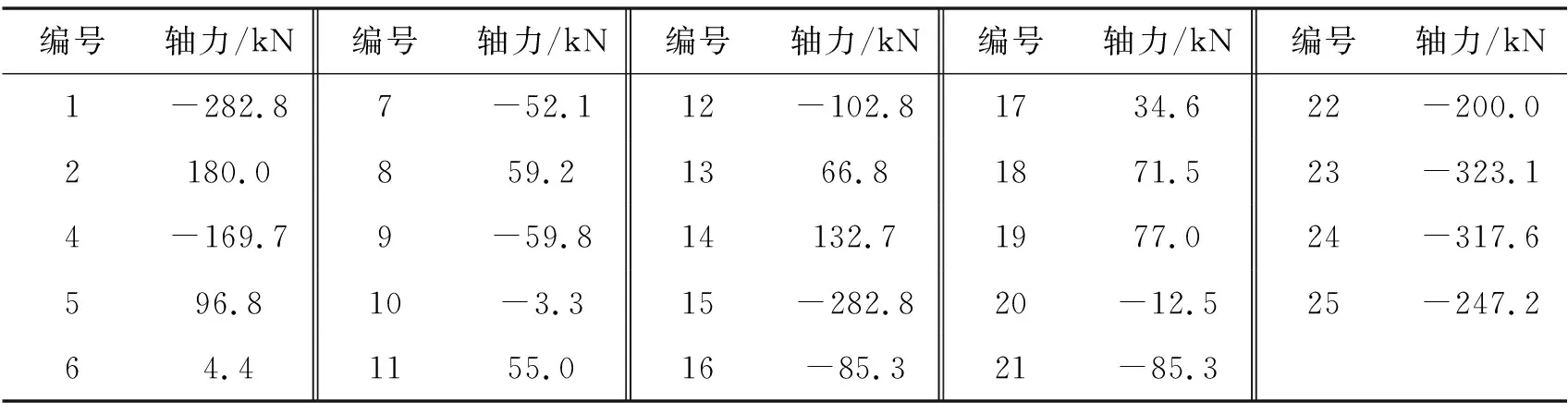
表6 3号杆件失效后各杆件计算轴力

当荷载系数为1.526时，13号杆件计算轴力超过自身极限承载力，杆件失效退出工作。荷载继续再分配，当荷载系数为1.709 1时，7、9号杆件同时失效。3、13、7、9号杆件都失效后，23、24号杆件计算轴力都超过自身极限承载力，结构体系整体破坏。因此LFd3=1.7091，rd3=2.27。失效路径为杆件3→13→(7,9)→(23,24)。

4号杆件失效后剩余结构荷载再分配见表7。

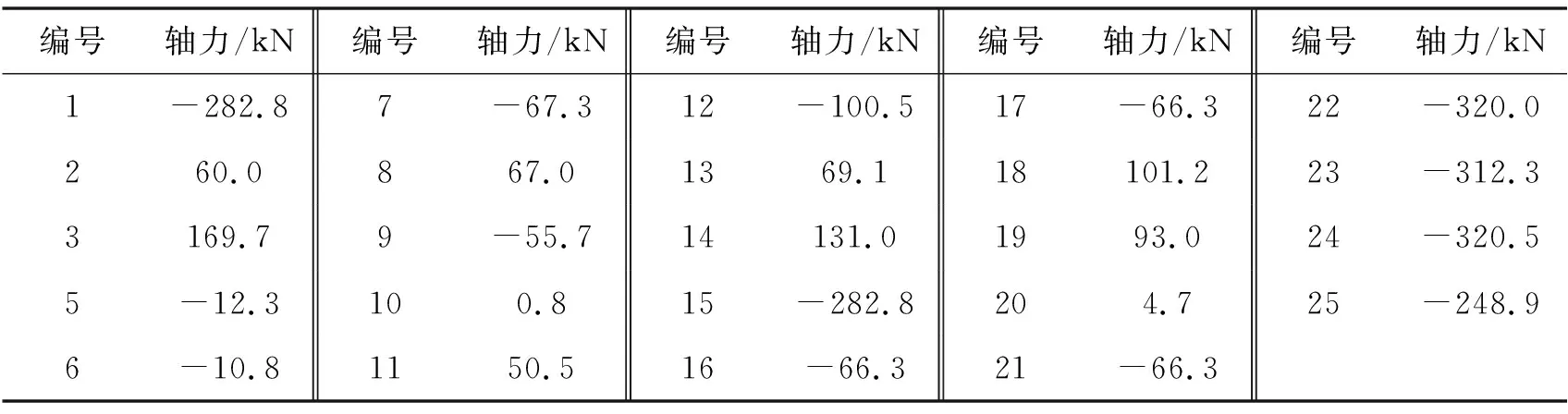
表7 4号杆件失效后各杆计算轴力

3号杆件计算轴力超过自身极限承载力。3号杆件也失效后结构体系成为可变体系，结构体系整体破坏。因此LFd4=0，rd4=0。失效路径为杆件4→3。

5号杆件失效后剩余结构荷载再分配见表8。

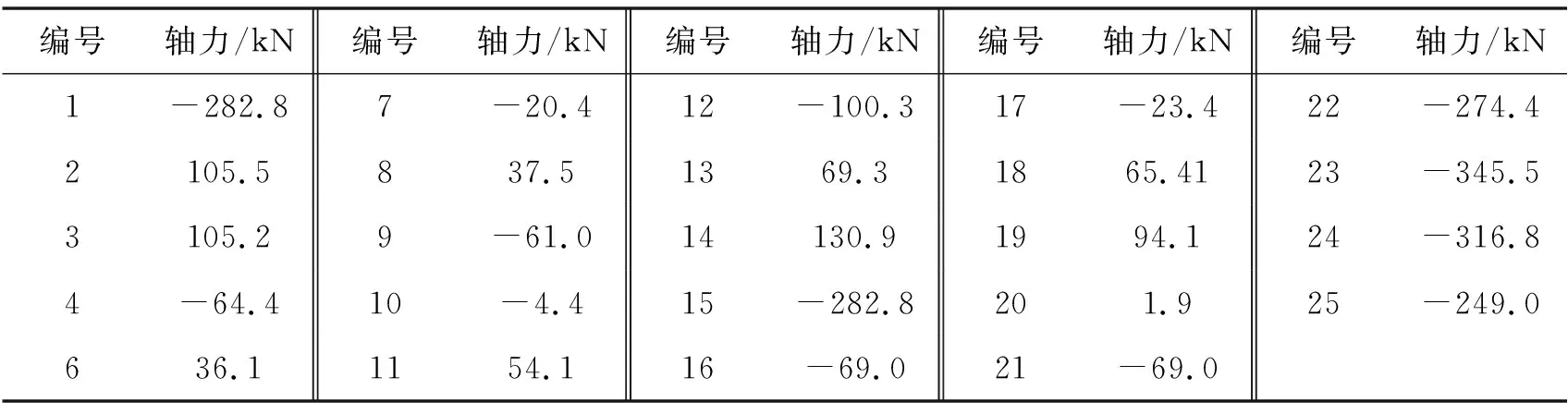
表8 5号杆件失效后各杆计算轴力

3号杆件计算轴力超过自身极限承载力。3号杆件也失效后6号杆件随之失效。结构体系在5、3、6号杆件失效后成为可变体系，结构体系整体破坏。因此LFd5=0，rd5=0。失效路径为杆件5→3→6。

6号杆件失效后剩余结构荷载再分配见表9。

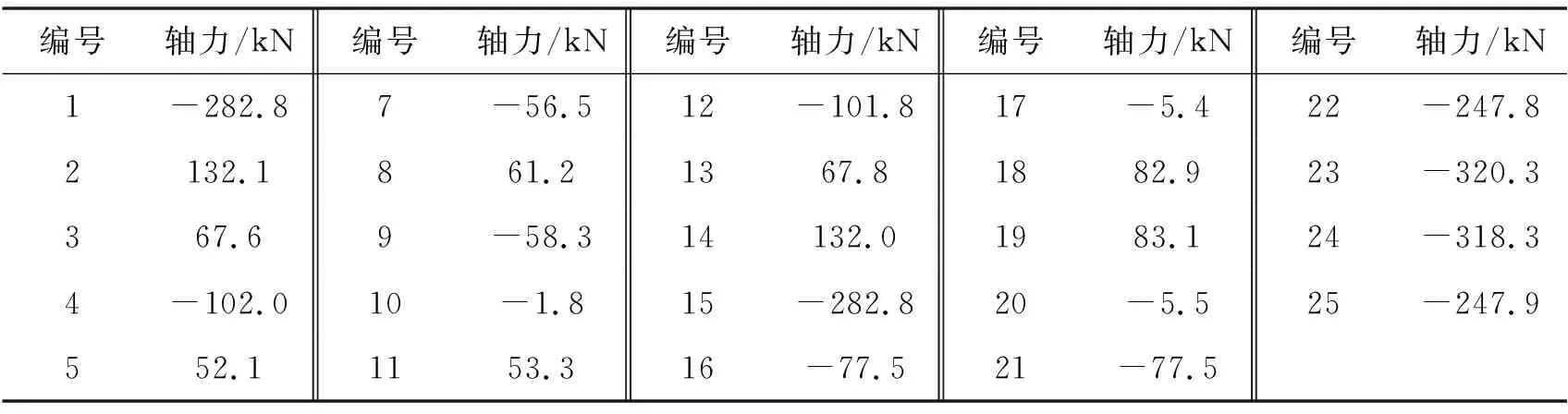
表9 6号杆件失效后各杆计算轴力

当荷载系数为1.504时，13号杆件计算轴力达到102.003 kN，超过自身极限承载力，杆件失效退出工作。6、13号杆件失效后，当荷载系数继续加大到1.627时，7号杆件计算轴力达到-92.044 1 kN,杆件失效退出工作。结构体系在6、13、7号杆件失效后成为可变体系。因此LFd6=1.627，rd6=1.081。失效路径为杆件6→13→7。

7号杆件失效后剩余结构荷载再分配见表10。

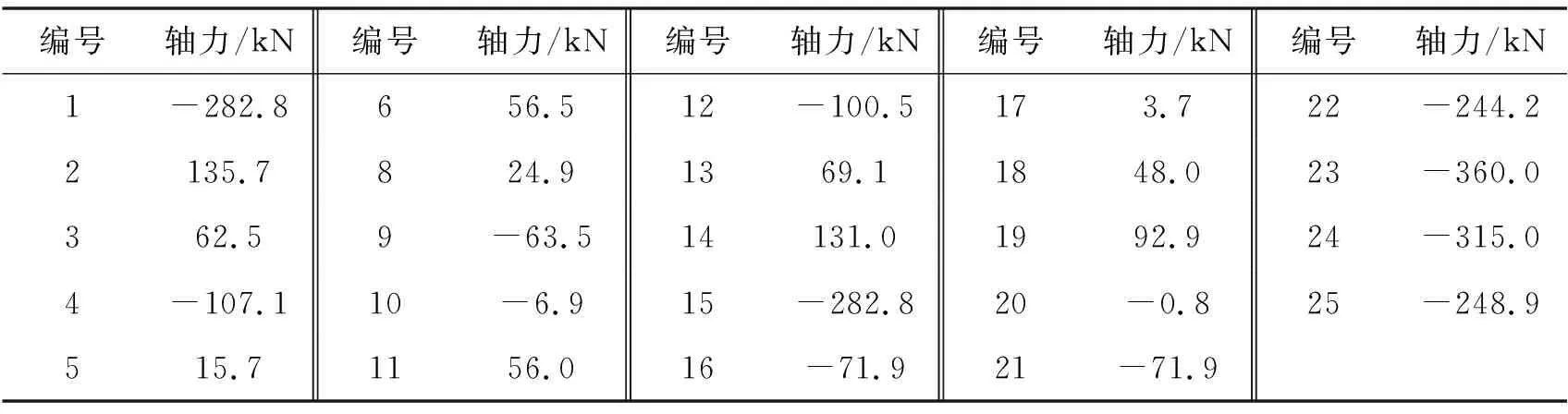
表10 7号杆件失效后各杆计算轴力

当荷载系数加大到1.449时，9号杆计算轴力达到-92.09 kN，超过自身极限承载力，杆件失效退出工作。7、9号杆件失效后，当荷载系数继续加大到1.604时，3、13号杆件计算轴力超过自身极限承载力，杆件失效退出工作。7、9、3、13号杆件都失效后，当荷载系数加大到1.704时，23、24号杆件轴力达到-613.45 kN，失效退出工作。结构体系在7、9、3、13、23、24号杆件失效后整体破坏。因此LFd7=1.704，rd7=2.26。失效路径为杆件7→9→(3,13)→(23,24)。

8号杆件失效后剩余结构荷载再分配见表11。

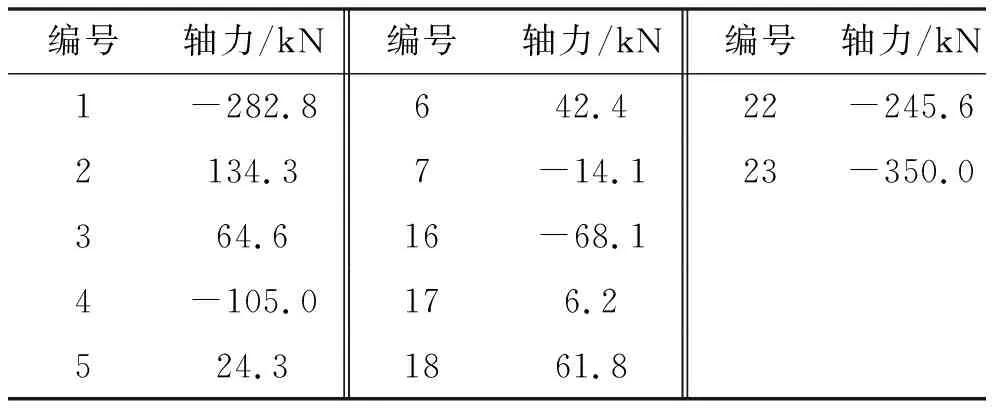
表11 8号杆件失效后各杆件计算轴力

荷载系数增加到1.579时，3、13号杆件计算轴力达到102.048 4 kN，杆件失效退出工作。8、3、13号杆件失效后，当荷载系数增加到1.753时，23、24号杆件计算轴力达到-613.55 kN，杆件失效退出工作。结构体系在8、3、13、23、24号杆件失效后成为瞬变体系。因此LFd8=1.753，rd8=2.33。失效路径为杆件8→(3,13)→(23,24)。

将初始设计时结构体系局部破坏冗余度结果汇总如表12所示(9～15号杆件与1～7号杆件对称，情况相同)。

由表12可以看出：1、2、4、5号杆件失效的局部破坏冗余度小于1，由式(3)、(4)可知初始设计的桁架体系在超载作用下系统的承载能力不足，若是1、2、4、5号杆发生失效，整个体系没有抵抗力。

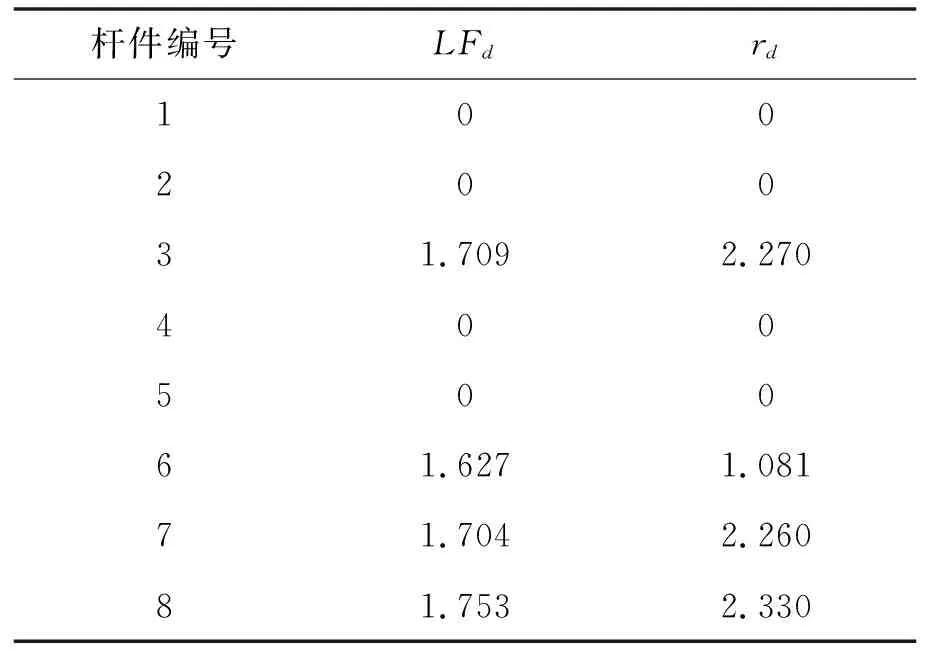
表12 初始设计下结构各种局部损伤冗余度

4 优化分析

1号杆件失效退出工作后结构体系立刻成为瞬变体系，没有其余的替代传力路径。因此1号杆件在结构体系中非常重要，在桥梁的使用过程中应做好保护措施。优化后的桁架体系应对2、4、5号杆件失效这几种局部破坏有足够的冗余度，同时应有足够的极限承载冗余度。

将3、13号杆件截面面积加大到16 cm2,6、10号杆件截面面积加大到7 cm2,23、24号杆件截面面积加大到50 cm2。优化后各杆件截面尺寸以及相关材料参数见表13。

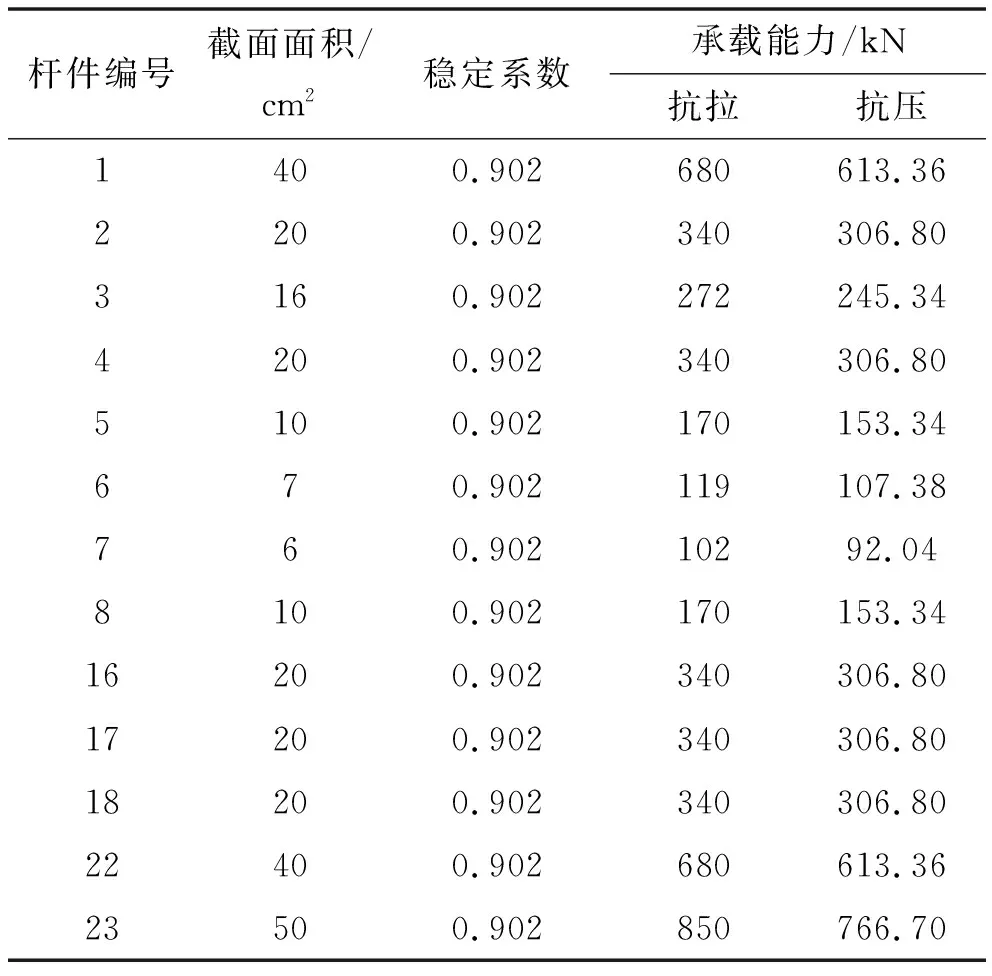
表13 优化设计后的杆件参数

分析优化设计后桁架体系的极限承载冗余度以及剩余7种可能发生局部破坏的冗余度。先求LF1和LFu。将荷载系数加大到1.581时，7、9号杆件的轴力达到-92.066 kN，杆件失效退出工作。荷载再分配后剩余结构体系继续承载，当荷载系数继续加大到2.104时，6、10号杆件的计算轴力达到119.020 2 kN，杆件失效退出工作。6、10、7、9号杆件都失效后桁架结构成为可变体系。因此优化设计后LFu=2.104，LF1=1.581。由式(1)、(2)计算得到ru=1.02。接着通过局部破坏冗余度分析结构体系可能发生的剩余7种局部破坏，即2～8号杆件失效后继续承载的能力。

2号杆件失效后，当荷载系数加大到1.069时，3号杆件计算轴力达到272.123 kN，杆件失效退出工作。桁架体系在2、3号杆件失效后成为瞬变体系。因此优化设计后LFd2=1.069，rd2=1.35。失效路径为杆件2→3。用同样的方法可以得到3～8号杆件失效后结构的局部损伤冗余度。

将优化设计后桁架体系易发生的7种初始损伤下的局部破坏冗余度汇总如表14所示(9～14号杆件与2～7号杆件对称，情况相同)。

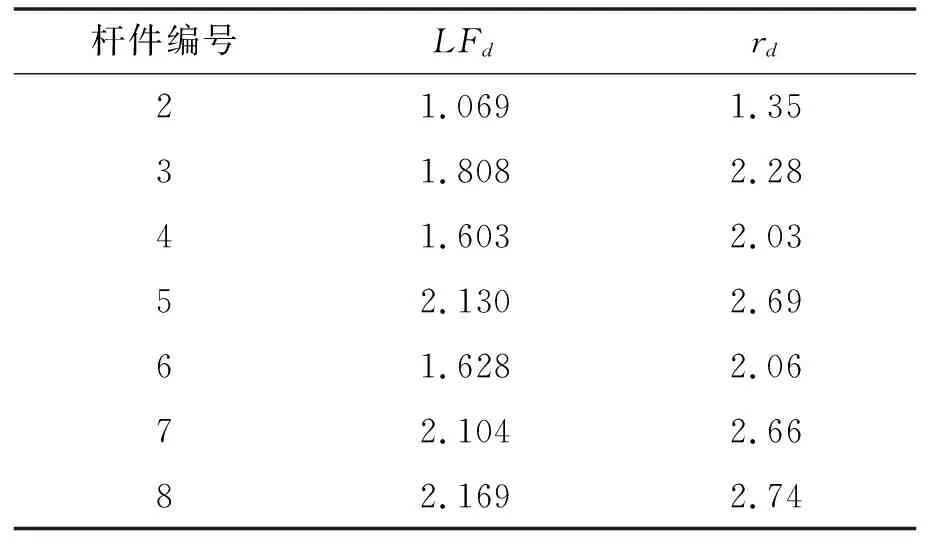
表14 优化后结构体系各种局部损伤冗余度

5 结论

为了使桥梁各构件充分发挥各自的能力，该文基于冗余度能够确定构件破坏顺序的优势，采用冗余度对桥梁体系进行优化设计。可得主要结论如下：

(1)冗余度方法可以有效确定结构体系的破坏先后顺序，所得破坏顺序即为体系的优化顺序。

(2)局部破坏冗余度和极限承载冗余度相结合可以量化桥梁结构在局部破坏发生后和超载情况下继续承载的能力，可为桥梁优化效果的评定提供理论支持。

(3)构件局部破坏冗余度是评定构件剩余承载力的主要标准，也是决定是否对构件进行加固，以及加固程度的主要标准。

(4)采用极限承载冗余度和局部破坏冗余度综合的分析结果可以确定构件及体系在超载或局部破坏下的承载能力，进而为桥梁优化提供支持。