深埋隧道底板锚杆支护关键参数研究——以松山隧道为例

冯劭博，肖克霖，于远祥，解智勋

(1.中交一公局第五工程有限公司，北京 100000；2.中交一公局集团有限公司， 北京 100024； 3.西安科技大学 建筑与土木工程学院，陕西 西安 710054)

随着我国公路交通事业的快速发展，一大批长大深埋隧道工程陆续开建，隧道施工普遍面临高地压、高孔隙水压及高地温现象的复杂工程地质环境[1]，极易出现底板隆起现象，严重影响正常施工和日后的行车安全.因此，如何合理确定隧道施工期间底板的支护方案及其参数成为有效控制底板变形的关键环节，大量专家也对隧道底板灾害进行了长期深入的研究.郑成果[2]提出隧道底鼓的防治包括预防和治理两方面，锚杆支护作为一种行之有效的隧道底鼓防治措施已被广泛应用于隧道等地下工程.贺建清等[3]运用弹性力学理论研究了桃树垭隧道底板的极限承载力及其塑性区发展区域，确定了底板锚杆的理论长度.田田等[4]确定了临海浅埋富水明挖隧道底板的合理支护参数.周栋梁等[5]以湘西某高速公路岩溶区分岔隧道为例，建立了不同破坏模式下岩溶区隧道底板的安全厚度预测公式.李晓俊[6]讨论了恒山隧道运营期间针对底板病害的换拱和注浆加固治理技术.腾俊洋等[7]通过数值模拟探讨了层状炭质页岩隧道的底鼓机理.程刚等[8]分析了金鸡峡岩溶隧道底板突水的处置措施.杨成永等[9]研究了地铁隧道底板结构隆起导致的轨道变形规律.

上述研究成果对正确认识特长深埋隧道底板破坏规律具有很好的借鉴意义.通常，隧道开挖后，围岩应力将发生重新分布，并在侧墙上方出现应力集中现象，在分析隧道底板变形及其支护参数时集中应力对的影响是不可忽视的.但现有关于隧道底板变形的研究并未考虑隧道侧墙上方集中应力的影响，隧道底板支护参数的设计具有很大的随意性和盲目性.本文在总结前人研究的基础上，通过建立松山右线隧道侧墙在集中应力作用下的受力模型，计算侧墙的极限平衡区；基于隧道底板的滑移线力学模型，确定底板的最大破坏深度及其位置，进而合理设计底板的初期锚杆支护参数.

1 工程概况

松山右线特长隧道(北京段)是延崇高速第9合同段的全线重点控制性工程.该隧道长4 700 m，最大埋深超过900 m.在里程K31+560～YK31+620III类段，隧道平均埋深为400 m，开挖断面如图1所示.该段隧道的地层岩性主要为燕山期兰角沟中粒似斑状二长花岗岩且细粒角闪花岗岩和兰角沟中粒似斑状二长花岗岩侵入接触.隧道地层断裂构造发育且为富水断层，断裂部位岩体比较破碎.该段隧道开挖初期，由于原初期在支护设计中忽略了对隧道底板进行锚杆加固，底板岩体在侧墙上方集中压力和衬砌结构压模效应的综合作用下向隧道内空发生挤压流动，其底鼓量达250～340 mm，如图1所示.

图1 松山右线隧道开挖断面示意图Fig.1 Schematic diagram of the excavation section of Songshan Right Line Tunnel

如何有效控制隧道开挖后底板隆起变形是本段隧道施工的重点和难点.从松山隧道底臌机理来看，施工现场地下水的水理作用加剧了底臌的发生和发展，但底板岩体在隧道侧墙集中压力作用下的挤压流动才是底臌形成的最本质原因，必须采取合理的锚杆支护措施才能有效控制该段隧道底臌的发生.

2 隧道侧墙及底板受力变形理论分析

2.1 隧道侧墙岩体变形受力分析

隧道开挖之前，岩层处于三维应力平衡状态.隧道开挖后，破坏了围岩原有的应力平衡状态，引起围岩应力重新分布，隧道周边围岩在径向卸载，而在切向侧墙上方形成应力集中区[10-11].侧墙岩体在其上方集中应力的作用下发生弹塑性变形，形成如图2所示的极限平衡区和弹性区.

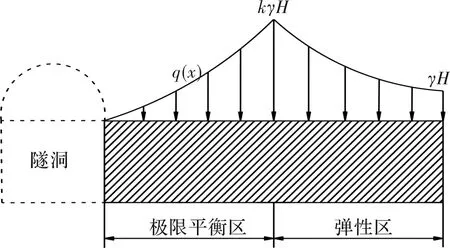
图2 侧墙集中压力计算模型Fig.2 Calculation model of concentrated pressure on side wall

由文献[12]可知，忽略侧墙岩体的体积力，极限平衡区内侧墙岩体与顶板之间界面上应力的基本方程为

(1)

由式(1)可得

解之得

(2)

式中：pi为侧墙支护阻力；h为侧墙高度；λ为侧压力系数；c0为粘聚力；φ0为摩擦角.

由图1可知侧墙岩体弹性界面x=x0处，有

σy=kγH

(3)

联立式(2)和(3)得

进而可得侧墙岩体极限平衡区宽度为

(4)

2.2 隧道底板变形受力及稳定性分析

2.2.1 隧道底板力学模型的建立

侧墙岩体将垂直集中荷载传递给隧道底板，当底板岩体应力状态达到或超过其屈服条件时，底板岩体将产生如图3所示的剪切滑动.

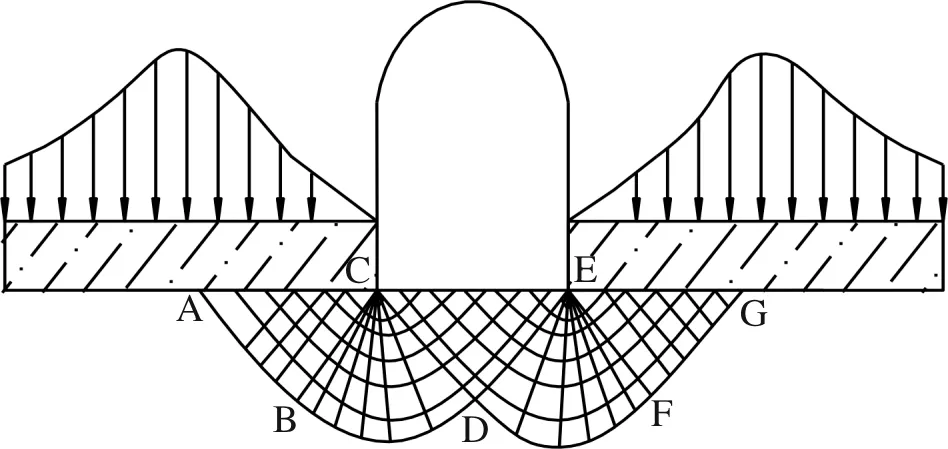
图3 隧道底板塑性破坏带分区Fig.3 The plastic failure zoning of the tunnel floor

当ABC和EFG区的岩体在垂直方向上受压缩而碎胀变形后，在水平方向上必然会挤压BCD和DEF的岩体，进而导致CDE区的岩体将向隧道空间内隆起而形成底臌.

2.2.2 底板破坏最大深度及其位置分析

由于对称性，选取图3的右半部分进行分析.建立底板力学模型如图4所示，其中EFG区和CED区的滑移线均为两组直线.而过渡区DHF的滑移线一组为对数螺线，另一组为以E为起点的放射线.

图4 隧道底板破坏深度计算模型Fig.4 The mechanical calculation model of the tunnel floor failure depth

设底板岩体的内摩擦角为φ1，对数螺线方程为

r=r0eθtanφ1

视△EFG为等腰三角形，其底EG即为侧墙岩体平衡区宽度x0，由三角关系可得

(5)

同理，在△OEH中，有

h=rsinα

(6)

对于△CEH仍可简化为等腰三角形，其中，

而在△EFG中，

由此得到

∠HEF=180°-∠CEH-∠GEF=90°.

进而有

所以

(7)

将式(7)代入式(5)即可得到

(8)

由dh/dθ=0，即可得底板最大破坏深度hmax.

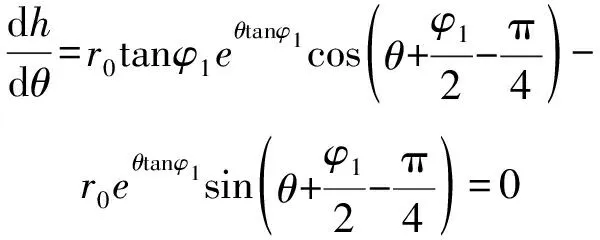
即有

从而得到

(9)

将式(5)和式(9)代入式(8)得隧道底板最大破坏深度为

(10)

在此基础上，由△OED可得最大破坏深度距侧墙表面的水平距离：

(11)

将式(7)和式(9)代入式(11)可得

l=hmaxtanφ1

(12)

2.2.3 隧道底板稳定性分析

由文献[13]可知，底板保持不发生底鼓的极限承载力为

(13)

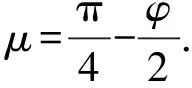
当松动围岩由两帮传递到底板的峰值应力大于底板极限承载力，底板将发生塑性流动，此时有

Δq=kγH-q≥0

(14)

当隧道底板在侧墙峰值集中应力达到或超过底板岩体的极限强度时，底板将发生剪切滑动，由式(13)和(14)可得

(15)

3 深埋隧道底板变形锚杆支护机理

3.1 有效阻止底板岩体剪切滑移

为阻止底板岩体的剪切滑动，通常需要在隧道底板及其两侧的墙角布设锚杆.基于隧道底板挤压变形破坏的力学机理，建立底板锚杆支护系统如图5所示.

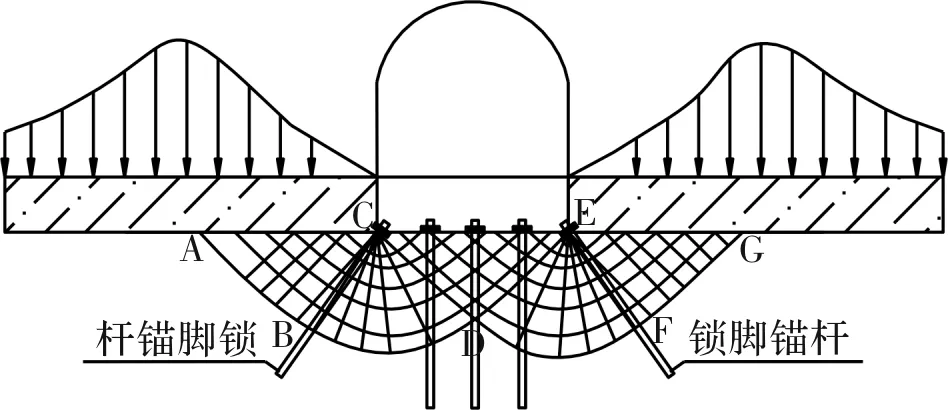
图5 底板锚杆系统布置示意图Fig.5 Schematic diagram of floor anchor system layout

隧道开挖后，侧墙在集中压力作用下，底板两墙角部位首先进入塑性状态，当底板岩体产生剪切滑移后，底板中间部位将向上隆起，同时隧道侧墙也随之下沉，进而影响到隧道拱部的稳定性.如果在两侧墙角部位施加锁脚锚杆，当杆体抗弯强度足够支撑底板岩体的剪切作用时，锁脚锚杆将抑制底板岩体的剪切滑动及隆起变形并阻止侧墙岩体的下沉，此时有[14-15]

(16)

qc=(ccotφ+ps)c1D

(17)

式中：pd为无支护时底板的极限承载力；qc为杆体阻力；c为底板围岩黏聚力；D为锚杆直径；φ为围岩内摩擦角；c1为与φ成正相关的阻力系数.

可以看出，当底板岩体施加锚杆后，其黏聚力c和内摩擦角φ均将有所增加，此时底板岩体的极限承载力也将得以提高.

3.2 有效削弱底板岩体挤压应力

将隧道侧墙挤压应力沿杆体轴向和垂直于杆体轴向进行分解，如图6所示.前者对锚杆产生拉应力，将部分挤压应力传递到底板深部；后者对锚杆产生弯剪作用，使锚杆绕底板基角旋转.在锚杆阻力作用下，降低锚杆上部岩体对下部岩体的挤压作用.

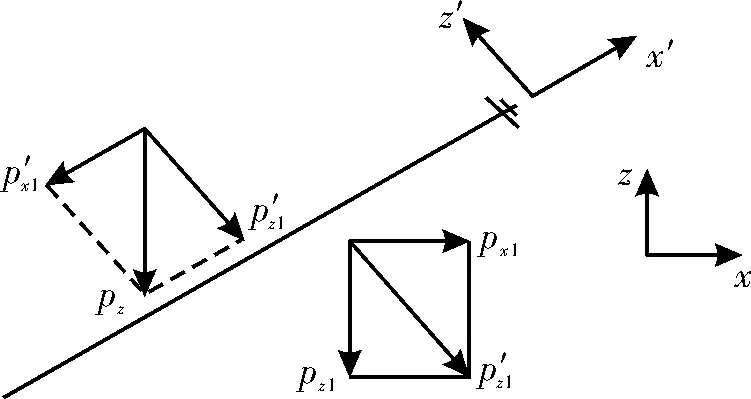
图6 底角锚杆分力效应示意图Fig.6 Schematic diagram of force component effect of bottom angle anchor

由图6可知

(18)

式中：pz为挤压应力；pz1为锚杆轴线方向和垂直于锚杆轴线方向分解的力.

可以看出，当α=45°时，Pz1值最小，锚杆支护效果最好.

隧道底板支护所用锚杆通常需穿过底板塑性区并锚入稳定岩层，当隧道底板中间部位的岩体向上隆起时必将对锚杆产生一个向上的拉拔力，而锚杆锚固段的周围岩体则对杆体产生向下的抗拔力，如图7所示[3].

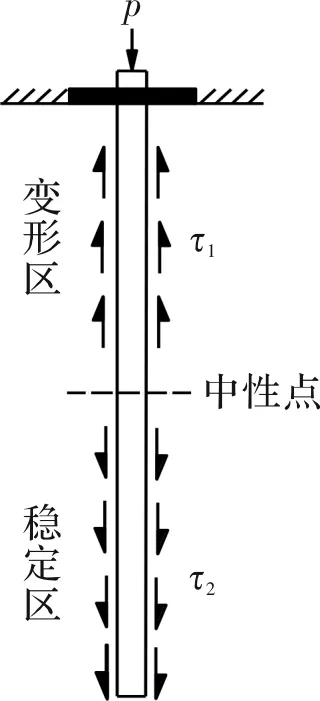
图7 底板锚杆受力模型Fig.7 Stress model of floor anchor

可以看出，底板锚杆的预紧力为向上拉拔力与向下拉拔力与的差值，其大小为

p=Δq×a×b

(19)

式中：a和b分别为底板锚杆的间排距.

3.3 底板锚杆选型分析

基于上述理论分析，为充分发挥底板锚杆对底鼓的控制作用，锚杆材料应尽量选用具有良好抗弯和抗剪性能的材质.此外，由式(15)和(16)也可看出，通过增加锚杆直径来提高锚杆强度，进而增加底板岩体剪切滑移所克服的杆体阻力，以增加底板岩体的稳定性.

4 松山隧道底板变形破坏力学分析

为验证上述理论在工程上的合理性，本文以松山右线隧道里程K31+560～YK31+620III类围岩段为工程实例，利用上述理论公式分析计算隧道两侧墙角及底板的锚杆关键参数.

4.1 松山隧道底板稳定性分析

经现场实测和试验可知，松山右线隧道里程K31+560～YK31+620III段底板岩体的力学参数如表1所示.隧道侧墙岩体力学参数如表2所示.

表1 隧道底板岩体力学参数Tab.1 Mechanical parameters of tunnel floor rock mass

表2 隧道侧墙岩体力学参数Tab.2 Mechanical parameters of tunnel sidewall rock mass

由公式(13)可知，底板保持不发生底鼓的极限承载力为

=10.21 MPa

(20)

而松山隧道侧墙峰值集中应力大小为

kγH=1.2×25×400=12 MPa

(21)

由(20)和(21)的计算结果可知，隧道底板将在侧墙上方集中应力的作用下发生剪切滑动，需对底板进行支护.

4.2 隧道底板最大破坏深度及其位置分析

将隧道侧墙设计高度h=4.6 m及表2中相关数据代入式(4)可得隧道侧墙的极限平衡区宽度为

(22)

将式(22)及表1的相关数据代入式(10)得隧道底板的最大破坏深度为

(22)

将式(22)代入式(10)得最大破坏深度距隧道侧墙壁的距离为

l=2.21×tan18°=0.72 m

(24)

5 松山隧道底板锚杆支护参数设计

5.1 隧道底板锚杆参数设计

5.1.1 隧道底板锚杆长度计算

考虑到理论计算和工程实际的误差，底板锚杆统一按最大破坏深度进行设计.当锚杆外露长度l1=0.15 m，锚入底板稳定岩层的长度l3=0.3 m，考虑安全系数K=1.2，则初期支护中底板锚杆长度为

L1=K×(l1+l2+l3)=1.2×(0.15+2.21+0.3)

=3.2 m

为便于施工，施工中底板锚杆可按3.5 m进行设计，其间排距根据工程实际设计均为600 mm，必要时可对隧道底板进行锚注联合支护.

5.1.2 隧道底板锚杆预紧力设计

由式(13)、(19)及(20)可得

Δq=12-10.21=1.79 MPa

(25)

取锚杆托盘尺寸为80 mm×80 mm×8 mm，由式(15)及(24)可得底板锚杆的预紧力大小为

p1=1.79×103×0.08×0.08=11.456 kN

5.2 底板锁脚锚杆参数设计

5.2.1 底板锁脚锚杆长度设计

由图4中可知，当锁脚锚杆的绕流阻力大于或等于隧道底板承载能力与侧墙集中压力的差值时，底板将处于稳定状态.由式(5)可得墙角锚杆有效长度为

当锚杆外露长度l1=0.15 m，锚入底板稳定岩层的长度l3=0.3 m，则隧道墙角锁脚锚杆的长度为

L2=K×(l1+l2+l3)=1.2×(0.15+1.61+0.3)

=2.47 m

为便于施工，施工中底板锁脚锚杆可按3 m进行设计.

5.2.2 底板锁脚锚杆预紧力设计

仍取锚杆托盘尺寸为80 mm×80 mm×8 mm，则底板锁脚锚杆预紧力为

基于上述理论计算结果，对松山隧道右线隧道里程K31+560～YK31+620III段底板岩体进行锚杆支护，如图6所示.

图8 松山隧道底板锚杆系统布置Fig.8 Layout of floor anchor system of Songshan Tunnel

采用上述方案对隧道底板采用锚杆支护后，底板变形在40 d后趋于稳定，如图9所示.松山隧道底板控制效果良好，为该隧道安全快速施工提供了有利条件.

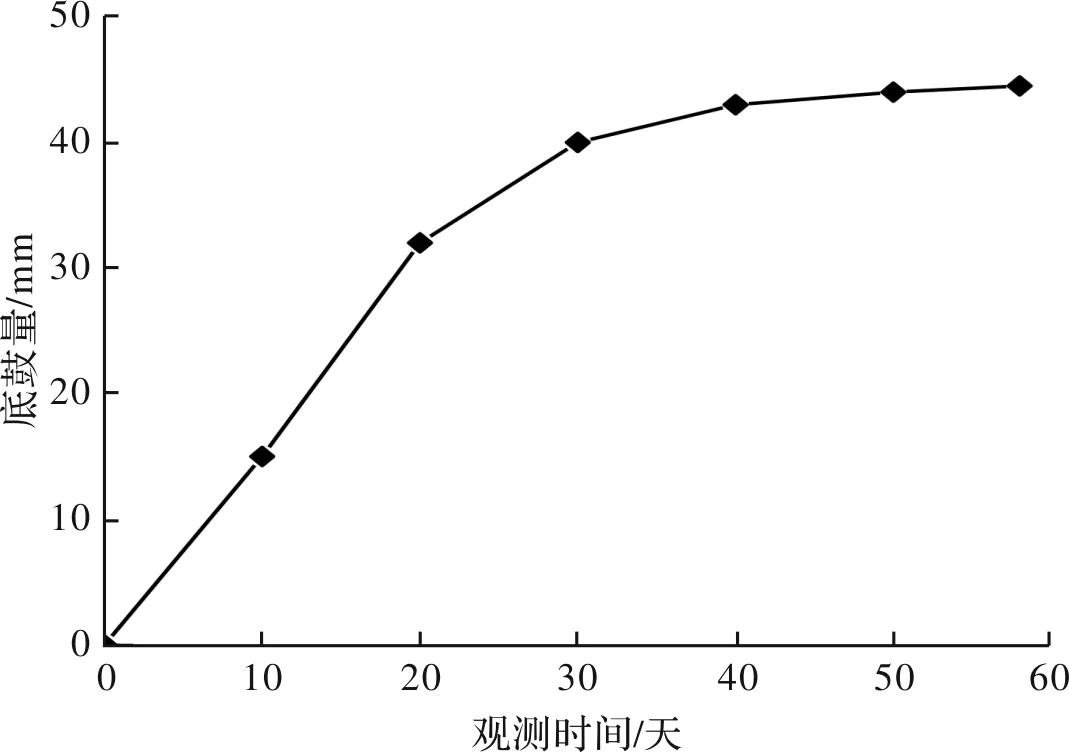
图9 隧道底鼓监测Fig.9 Tunnel bottom heave monitoring

6 结 论

(1)隧道开挖初期，由于围岩应力发生重新分布，隧道侧墙在上方集中应力的作用下将发生弹塑性变形并形成一定宽度的极限平衡区；

(2)当隧道侧墙上方的集中荷载超过底板的极限承载力时将出现剪切滑动，底板的最大破坏深度取决于侧墙岩体的极限平衡区宽度及底板岩体的内摩擦角；

(3)基于隧道侧墙的极限平衡区和底板滑移线场理论分析计算了松山隧道底板初期支护锚杆的长度、预紧力及间排距等关键参数，结果表明本文确定锚杆支护参数具有一定的科学性和合理性.