基于数字图像相关法在建筑结构变形场中的抗噪研究及应用

张 武，赵 亮,2，徐 琳，王 凡，卢 英

(1.西安建筑科技大学 信息与控制工程学院，陕西 西安 710055 ；2.西安建筑科技大学 土木工程学院，陕西 西安 710055)

混凝土结构性能随着服役时间的延长逐渐降低，因此，需要对结构进行检测.近些年来，对于混凝土结构检测的方法在不断地增加和完善，但是由于实验力学传统测量方法(光弹法、云纹法等)自身的局限性对混凝土的检测造成了影响，因此，数字图像相关方法(Digital Image Correlation，DIC)[1-3]因其非接触式、全场性测量、实验设备、测量环境要求低等优点被广泛地应用在实际测量中.

国内外众多学者都采用数字图像相关法对材料性能进行了研究，Castro等[4]利用数字图像相关装置测量变角度缠绕丝筒的几何缺陷；Shahmirzaloo等[5]采用数字图像相关方法绘制了Al2024搅拌摩擦焊接头不同焊接区域的局部应力-应变曲线来研究其局部本构特性；陈学文等[6]提出了一种连续高温损伤模型，利用数字图像相关技术捕捉X12合金钢试样的动态裂纹萌生和扩展的图像,并与裂纹位置与开裂顺序的模拟结果进行比较,定量评估了该模型在不同应力三轴度下的准确性.目前，在数字图像相关法的研究中，影响数字图像相关方法测量精度的主要因素(图像噪声[7-8]、散斑质量等[9-10])被深入讨论，其中噪声对精度的有很大的干扰.在实际测量中，由于采集系统和环境的影响，不可避免地会产生噪声.为了提高数字图像相关法的抗噪能力，Sutton等[11]提出了结合GCV(Generalized Cross Validation)和有限元的平滑算法减少噪声的影响；Pan等[7]提出一种选择合适子块大小的方法准则来确定子块的大小，进而减小噪声对算法的影响.以上研究虽然提高了数字图像相关法的抗噪能力，但在研究中存在各方面的问题.郑成林等[12]将Tikhonov正则化应用在图像灰度梯度的计算，取得了良好的抗噪效果.然而相比传统的Tikhonov正则化，Huber函数正则化[13]具有更好的稳定性和精度.

因此，本文提出一种新的数字图像相关法测量混凝土表面变形，采用Huber函数正则化灰度梯度的N-R法进行亚像素的配准来提高数字图像相关法的抗噪能力.通过新算法获得单轴压缩下混凝土的应变场，结合应变云图与应力应变曲线，分析混凝土破坏过程的各阶段，为研究荷载条件下混凝土开裂破坏过程提供可视化方法和新的试验手段.

1 基于Huber-N-R的数字图像相关法

(1)

式中，δ为误差(已知常数)，i=0,1,2….

为了求得灰度梯度y′(x)的近似值y*(x)，将数值微分转化为以下积分，即

(2)

式中：y*(t)为待求项；K(x,t)为核函数.

将式(2)构造为以下泛函数，即

(3)

式中：α为正则化参数且α>0；T(y*)为稳定泛函数.

Tikhonov正则化的泛函数T(y*)为

(4)

全变差正则化的泛函数T(y*)为

(5)

文献[13]将Huber函数引入泛函数φ(y*)作为稳定项T(y*)为

(6)

Φ(y*(t))为Huber函数，表达式如下，即

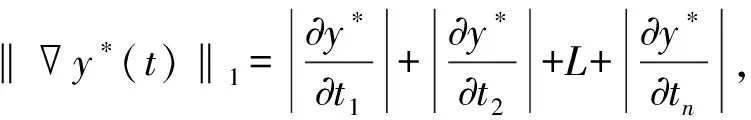
则本文的泛函数φ(y*)为

(7)

(8)

忽略误差，得

(9)

用有限差分法进行离散正则化项为

(10)

令t=ηh，带入式(10)，得

(11)

式(10)的离散型泛函数为

(12)

(13)

式中：A*是A的伴随算子；L(y*)=hD*D，E(y*)为对角矩阵，即

数字图像相关法进行混凝土结构的变形时，首先通过整像素搜索算法计算出变形的整像素位移，然后通过本文所提算法计算得出混凝土图像子区的灰度梯度后，与Newton-Raphson算法相结合，对混凝土表面的亚像素位移进行测量.

2 计算机模拟散斑可控变形验证

为了验证提出算法的正确性及准确性，采用计算机仿真可控散斑来模拟混凝土表面变形.仿真实验可根据需求对生成的散斑图像的尺寸、数目、光强及变形信息等进行精确地控制.计算机配置为Intel Core i9-11900K处理器，64.00 GB内存，MATLAB软件版本为2020b.采用zhou[14]等人提出的高斯散斑模拟物体表面变形过程：

(14)

式中：s为仿真实验中混凝土表面损伤特征点的数量；R为特征点点的半径；I0为特征点的最大光强(取值范围为0～255)；u0、v0为x、y方向上的位移，ux、uy、vx、vy分别为位移在各方向上的一阶导数.这里选取特征点颗粒数s为2 000，图像分辨率为512×512，最大光强I0=255，特征点颗粒半径r为2，其余参数为0.图1所示为基于MATLAB软件生成的数值模拟散斑图.

图1 模拟散斑图Fig.1 Simulated speckle pattern

为证本文算法的测量精度，采用计算机模拟散斑图对比实验对梯度法[15]、N-R法[16]、Tikhonov法和本文算法进行分析.选择特征点颗粒数s为1 200分辨率为256×256，散斑大小为4 pixel的模拟散斑图作为参考图像，将其沿x方向依次平移0.1,0.05,1,…,1.0 pixel，生成20幅散斑图作为变形后图像，不加入噪声，分别使用上述四种算法对其进行计算，实验结果如图2所示.

由图2(a)、(b)可看出四种算法的均值误差都在较小的范围内进行波动，但是梯度法的均值误差相较于其他三种算法来说波动较大，且标准差也一直高于其他三种算法；N-R法、Tikhonov方法和新算法的均值误差、标准差都基本相同.因此，在无噪声状态下，梯度法的测量精度误差较大，其他三种算法基本保持一致.

图2 各个算法的无噪计算误差比较Fig.2 Comparison of noise-free calculation errors of each algorithm

由上述实验可知，在进行亚像素配准计算时，梯度法的测量精度误差较大，不能应用在实际测量中，因此利用计算机模拟散斑实验对剩余三种算法的抗噪能力进行对比.选择特征点颗粒数s为1 500图像分辨率为256×256，散斑大小为4 pixel的模拟散斑图，将其沿x方向平移0.5 pixel作为参考图像，再加入均值为0、方差为10-6,10-5.5,…,10-2的一组高斯噪声，生成9幅变形后图像.分别使用上述四种算法对其进行计算，实验结果如图3所示.

由图3(a)、(b)可看出，三种算法的标准差和均值误差都随着噪声的增加而增加，N-R法的标准差和均值误差最大， Tikhonov法的标准差和均值误差增幅较小且远小于N-R法，新算法在三种算法中标准差和均值误差最小.因此，在有噪声的状态下，新算法在计算灰度梯度时产生的计算误差减小，提高了亚像素配准的精度和稳定性.

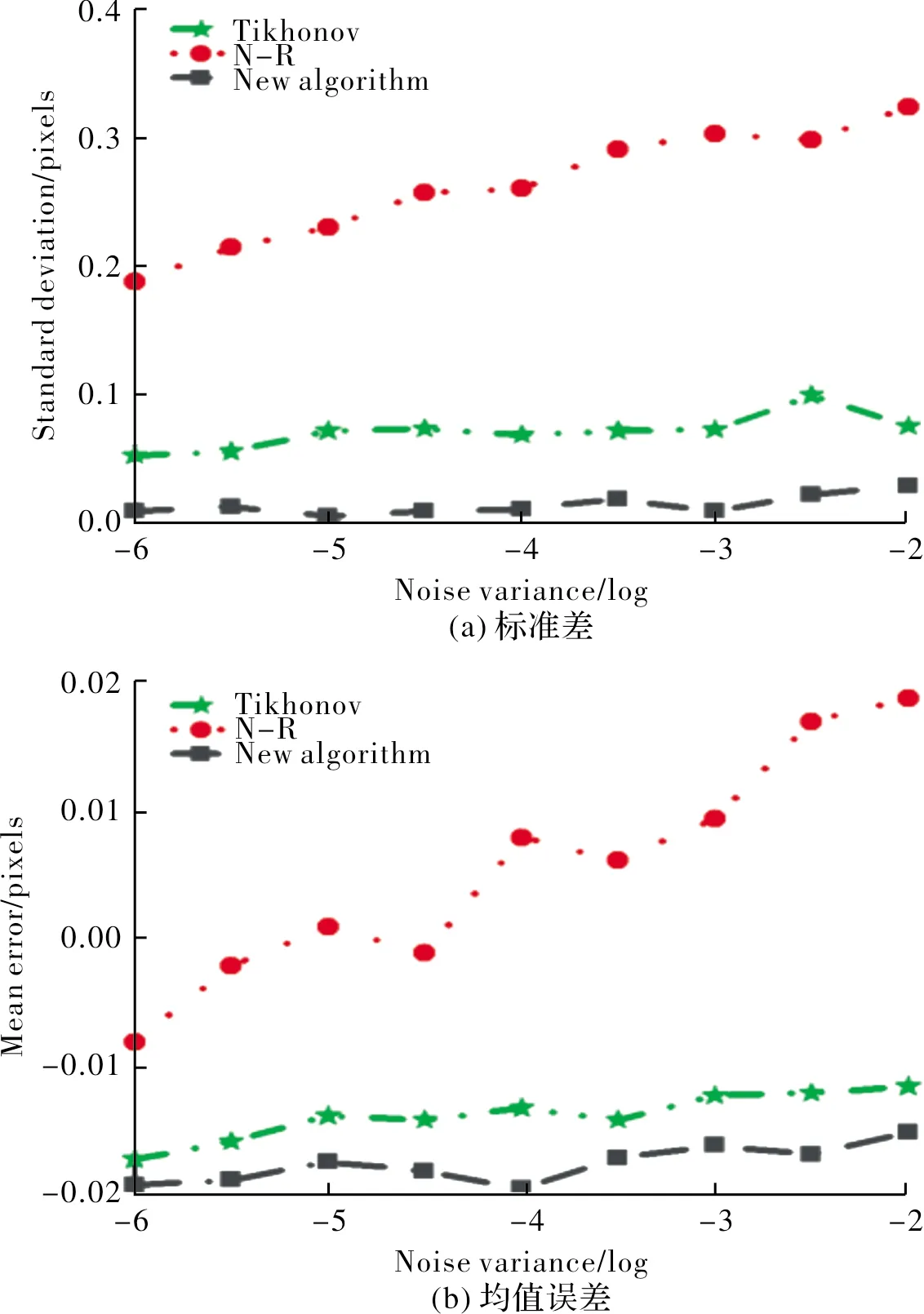
图3 各个算法的抗噪性能比较Fig.3 Comparison of anti-noise performance of each algorithm

3 混凝土单轴压缩变形测量试验

为验证算法在真实变形中的可靠性及实际应用性能，本文采用混凝土单轴压缩试验数据作为验证数据.试验对象为C60混凝土试件，采用西安建筑科技大学土木工程学院的WE-30型电子万能加载试验机(如图4所示)测量弹性模量试验，最大承重荷载为300 kN，测量精度≤±1%.试验前对混凝土试件表面进行人工诱导损伤，图像采集系统为高清照相机，试验过程采用LED直流光源进行补光.试验过程中，混凝土位移场的测量时产生的误差是由于算法系统误差、相机发热，镜头畸变、拍摄采光、振动噪声等问题引起.

图4 试验加载设备Fig.4 Test loading equipment

试验得到混凝土应力-应变曲线，如图5所示，将该曲线上不同时刻的点对应的应变云图绘制于图6.根据全场的应变云图可以清晰地从应变场分析混凝土单轴压缩下的裂纹演化规律，从细观角度观察混凝土试件的全局损伤特征.

由图5可以看出，1时刻为荷载施加初期，对应于图6(a)的应变云图，此时刻试件应变较小，此后，随着荷载的增加，混凝土压应变增加.图5中2时刻混凝土试件上出现了微小裂缝，试件开始微破裂阶段，表面开始不平整，所对应的全场应变云图如图6(b)所示，在云图中出现了不均匀化的应变区域，试件的左上方区域和底部偏上区域尤为明显.3时刻对应图6(c)所得的应变云图，此时在试件的左上方已经出现了应变集中区域，此时裂纹并未贯穿整个试件，此后应力应变曲线呈凸形，试件进入塑性阶段，应变急剧增大.到达4时刻时，由图6(d)可看出此时裂纹已经贯穿整个试件并且表现有较大变形，应力也达到了最大，试件遭到了破坏，但是此时试件并未完全碎裂仍能基本保持棱柱体形貌.此后，应力不断下降，混凝土破坏，但仍具有一定的承载能力，随着应力的变化，试件继续受应力作用，裂纹不断拓展直至整个试件完全碎裂.5时刻混凝土已完全破坏，由图6(e)亦可看出，此时的大应变集中区域遍布整个试件，此时试件表面已经布满裂纹，无法继续承载.

图5 应力应变曲线Fig.5 Stress-strain curve

图6 各个时刻下的应变云图Fig.6 Strain cloud diagram at various moments

此外，为了验证本文算法在实际噪声环境中的抗噪能力，进行了另一组实验，在试验机处于工作状态时采集试件表面图像，试验机工作时的振动噪声会使得混凝土试件表面产生微振动，而且影响成像设备的图像质量.此时，对混凝土试件不进行任何操作，试件的理论位移为0 pixel.利用数字图像相关法对上述采集的图像进行计算，结果如图7所示，由图可以看出，混凝土表面产生了位移，因此，可以通过计算上述图像的位移误差来对比算法的抗噪能力.

图7 混凝土位移场Fig.7 Concrete displacement field

分别使用三种算法对两幅散斑图进行变形场测量.表1为理论位移为0 pixel时三种算法的误差和运算时间，由表1可知，N-R法和Tikhonov法的均值误差分别是本文算法的2.5倍和1.5倍，标准差分别是本文算法的3.5倍和2倍，本文算法相比N-R法和Tikhonov法计算效率别提升了20%和10%.在实际的噪声环境中，相比N-R法和Tikhonov法，Huber函数正则化方法所得的灰度梯度可以有效减小噪声对测量值的影响，提高了数字图像相关法在混凝土变形测量中的抗噪能力，提高了数字图像相关法的计算精度和计算效率.

表1 理论位移为0 pixel时三种算法的计算误差和运算时间Tab.1 The calculation error and calculation time of the three algorithms when the theoretical displacement is 0 pixel

4 结论

本文将数字图像相关法应用于混凝土结构变形测量中，为了解决传统检测方法繁琐、不易操作及对建筑结构有损害等问题.得到了以下结论：

(1)本文提出了一种新的数字图像相关法来提高数字图像相关法在混凝土测量中的抗噪能力.进行了数字仿真实验和混凝土单轴压缩变形测量试验验证了新算法的可靠性和准确性；

(2)通过新算法得到混凝土单轴压缩试验下的应变云图，分析了混凝土破坏过程中四个阶段，为研究荷载条件下混凝土开裂破坏过程提供可视化方法和新的试验手段，并进行了新算法抗噪试验对比，得出了新算法在抗噪方面拥有更好的优越性.