鱼形仿生柔性翼结构设计及优化

秦伟伟， 左新龙， 张 建， 蒋苏豫， 唐文献

(江苏科技大学机械工程学院， 镇江 212100)

鱼类经过数十亿年的自然选择，进化出了多种多样的种类，拥有着多样式游动方式。这些种类与自己相匹配的游动方式相结合，使得它们可以在水里灵动地游动。鱼类的推进效率可达 80%。金枪鱼、海豚或鲸等采用月牙尾推进模式，其游速最高可达到20 km，且身体类似刚性结构，可以长时间低能耗地远距离迁徙[1]。月牙尾的拍动形成一个高效的推进器，类似一个振动的机翼。再如，黄斑狗鱼，这种鱼可以在非常短的时间内产生20g(g为重力加速度)的加速度；还有黄鳍金枪鱼在捕食过程中瞬时速度可以达到40多节[2]。因此，鱼类等水生生物这样优异的游动能力吸引了大批学者的目光。然而，中外关于水下柔性翼的研究相对较晚,现在的主要研究集中在水生物的波动和扑动推进方式,对水下柔性翼的推动机制研究不够深入。对于靠尾鳍摆动推进的鱼类,其推力是靠尾鳍摆动产生的,学者们已经发现了尾鳍的涡流场会极大地影响鱼类的推进性能。Lighthill[3]将航空领域的“细长体理论”引入到鱼类涌动的流体力学分析中，提出适用于身体侧向波动的“非稳态细长体理论”，建立了鲹科模式推进的数学模型；艾贤祖等[4]研究了摆幅对金枪鱼尾鳍推进性能的影响，验证了IBM(immersed boundary method)方法模拟尾翼非定常流动的有效性，实现了仿金枪鱼尾鳍在流场中的复合运动进行模拟，获取了尾鳍表面压力分布及尾涡涡量的分布，得到不同尾鳍摇摆幅度对推力系数及效率的影响差别，提取了利于提高推进性能的摆幅影响规律；崔祚等[5]对鱼的游动效率进行了分析，鱼体的内部肌肉和外部流体之间存在能量的传递和转换，鱼体摆动给周围流体传递机械能，该部分能量使鱼体发生弯曲摆动，该能量的反作用力就是鱼体向前的游动推力,传递的效率越高，游动效率就越高；姜兰兰[6]探讨了仿生鱼推进器结构设计的初衷和设计，当前仿鱼推进器驱动大多使用电机，这只能实现宏观上的仿生，很难实现结构仿生和微观行为仿生，利用仿生功能材料制造仿生肌肉，可以提高仿生推进装置的输出力和功率；李毅等[7]研究了柔性胸鳍的设计及柔性摆动，在设计时胸鳍是采用了简单的梯形，使得柔性翼在摆动时产生最大的推力以及最小的阻力；Cubero[8]总结采用柔性胸鳍和肢体扑动推进方式，相比于传统螺旋桨推进方式可提升近2倍效率；王田苗等[9]总结了中央鳍、对鳍推进模式仿生自主水下机器人的发展现状，指出了现有仿生AUV(autonomous underwater vehicie)研制所存在的问题。与常规鱼类尾鳍摆动推进方式相比，三维空间内多自由度的运动方式和柔性变形，采用柔性扑动推进方式的结构在运动时常伴随着复杂的流体动力特性，适用于尾鳍扑动的三维流动等经典理论无法用于柔性鳍的推进机理理论研究。因此，生物体的柔性结构扑动机理研究工作相比其他推进模式落后，理论体系尚未成熟，且鱼尾部(下躯干)与尾鳍的柔性结构推进方式因其复杂的非线性、耦合特性，还需大量工作亟待研究。本论文主要研究的是下躯干的仿生结构,形成具有机动性、稳定性、低能耗、低噪声等多种优异生物特性的结构模型。

折纸最早起源于中国，发展于日本[10]。折纸结构具有可以让材料趋于沿着预设折痕发生局部变形的特点，最近一些年正在变成一门新兴的工程技术。汽车的防撞设计、航天器的缓冲着陆等多个领域已经在应用这门技术，来改善减振器的变形模式，有效地提高其减振能力[11-16]。因此，将经过合理设计的折纸结构应用到鱼形仿生柔性翼的连接板上，通过其对材料的变形控制来改善柔性翼受压屈曲失稳的问题，具有重要的理论意义和使用价值[17]。

现开展鱼形仿生柔性翼设计及优化工作，通过循环水池实验，表征出锦鲤在水里游动的姿态，采用简单的折纸结构对鱼形仿生柔性翼进行设计，建立鱼形仿生柔性翼的模型，研究其驱动载荷和振动幅值的特性，并且通过正交试验设计，分析鱼形仿生柔性翼主要几何参数对其性能的影响规律和其回弹性能，并给出不同的参数组合，找到最优的方案。

1 鱼躯干生物学试验

1.1 外形特征统计分析

鱼的身体由头部、躯干、尾部三部分组成，躯干又分为上躯干和下躯干两部分，如图1所示。鱼的最普遍最重要的运动方式是全身肌肉运动，即利用躯干和尾部肌肉的交替收缩，让身体左右扭动击动水流，鱼借助击打水产生的反作用力，将身体推动向前。

图1 鱼结构图

选取20条锦鲤作为统计对象(品种为大正三色锦鲤)，使用钢卷尺(量程为0～3 000 mm，精度为1 mm)采集锦鲤的(腰-尾)长、尾宽、尾侧宽、腰宽、腰侧厚、最大摆尾幅度，使用量角器采集锦鲤的尾夹角。经分析取各项特征数据的均值作为仿生柔性翼设计与建模的数值，如表1所示。

表1 锦鲤外形特征统计

1.2 躯干运动姿态试验

躯干运动实验装置如图2所示，实验装置为一个循环水道(截面积为15 876 mm2，流速为3 m/s)，通道前后有渔网包裹，防止水流将锦鲤冲走，水道下方放置一面倾斜45°的镜子，可以从底部更好的观察到锦鲤的游动状况，了解锦鲤的运动姿态。正前方是一台相机用来记录锦鲤的运动姿态。

图2 循环水道实验

通过图片描画锦鲤姿态曲线，形成模态线，如图3所示。并选取T/4、T/6、T/12(T为周期)时刻作为主要参考，便于后续的拟合检验。

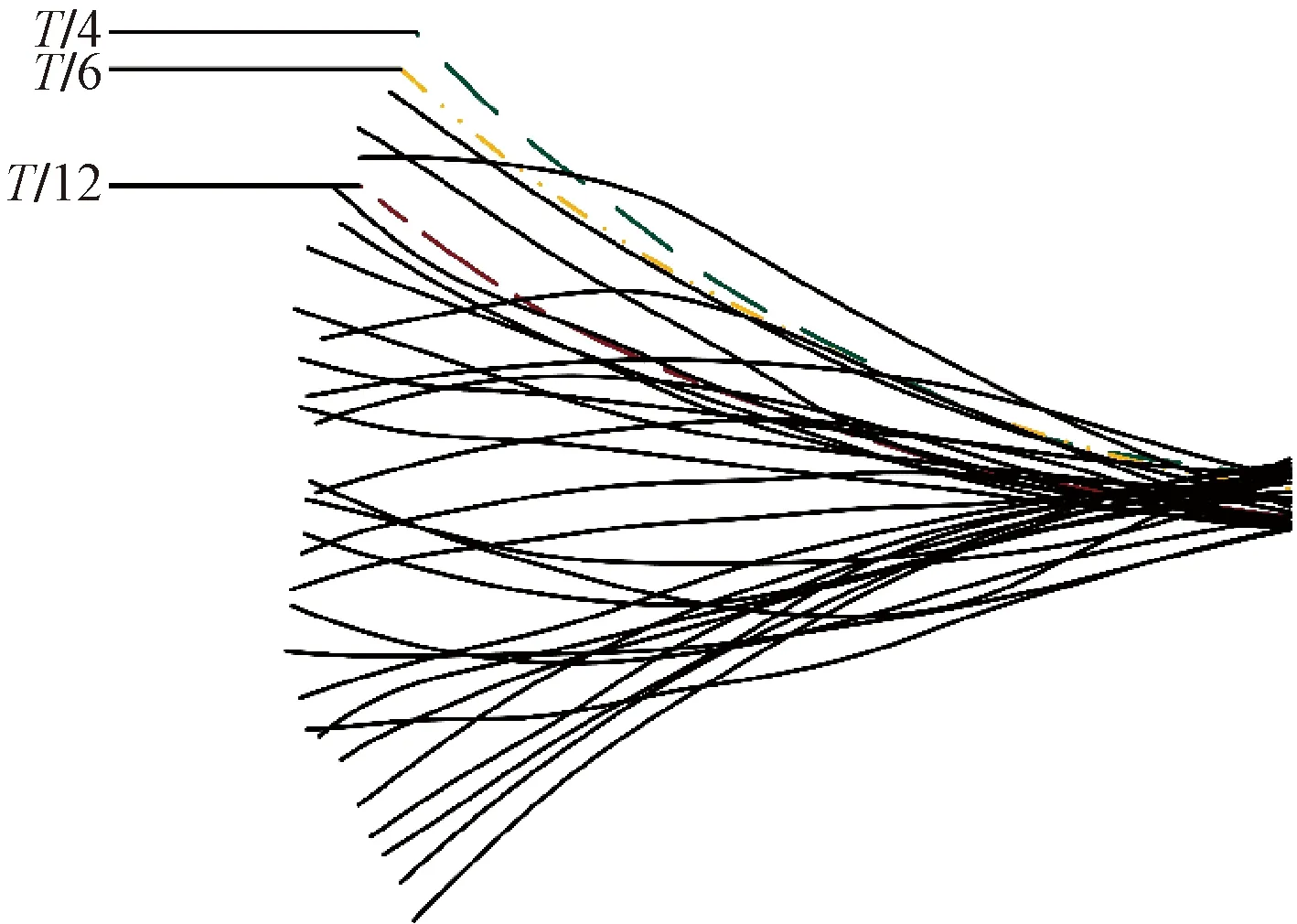
图3 躯干运动姿态模态图

2 仿生柔性翼设计与建模

基于鱼类的游动特性，本文设计的鱼形仿生柔性翼，主要是模仿鱼的下躯干的形状。与其他人研究不同的是这里的内板采用了简单的折纸结构。折纸结构相比于横板结构，优点在于能够让外板的拉推跟摆动更加的流畅，减少在流体中摆动的阻力。本结构一共设置两块内板，分别在仿生鱼的尾端和中部。如图4所示，柔性翼主要几何参数包括内板厚度t1、外板厚度t2、外板长度S、内板跟外板夹角θ、仿生柔性翼尾宽n和腰宽m，并且在模型的顶部、中部、1/4部分别取点A、B、C，以便后续观察。

图4 仿生柔性翼结构示意图

运用HYPERMESH将鱼形仿生柔性翼的每一块进行网格划分，相对称的地方网格的大小数量相同，以消除网格大小数量的不同对软件分析的影响，单元类型为线性四边形单元S4。利用有限元软件ABAQUS对鱼形仿生柔性翼结构进行驱动载荷和振动幅值的分析。为了模仿鱼类在水里的摆动，完全约束一边的外板，在另一边的外板上施加周期性往复的强制位移如图5所示，设置完毕，提交运算。选用的材料是304不锈钢，杨氏模量为190 GPa，泊松比为0.3。

图5 仿生柔性翼分析模型

3 结果分析与讨论

3.1 运动姿态试验对比分析

将图3中标注的T/4、T/6、T/12时刻的姿态跟仿真的同时刻的姿态进行对比，如图6所示，可以清楚地看出来一一对应的姿态相近，算出T/4时刻两姿态偏差为1.46%，T/6时刻两姿态偏差为0.32%，T/12时刻两姿态偏差为0.51%。这就可以看出拟合和仿真姿态偏差很小，拟合较好，设计合理。

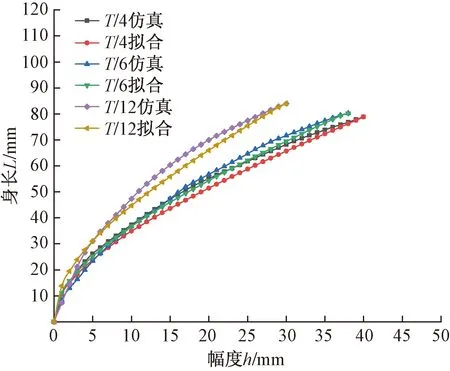
图6 T/12、T/6、T/4时刻姿态对比图

为验证设计结构的合理性，在鱼形仿生柔性翼上取三个点，如图4所示的A、B、C三个点，将这三个点实验中鱼摆动的幅值跟仿真时摆动的幅度都描绘出来进行对比，如图7所示。通过计算可以得出，在A点处，仿真跟拟合的偏差数值为8.13%，在B点处，仿真跟拟合的偏差数值为3.92%，在C点处，仿真跟拟合的偏差数值为0.82%，可以看出在这三点的偏差数值都比较小，数据表明拟合程度好，设计合理。

图7 T/4周期内A、B、C处摆动幅值对比图

经过上述不同时刻的姿态对比和同一时刻的不同位置摆动幅值对比，可以看出仿真跟拟合的轨迹相近，偏差较小，最大偏差仅为8.13%，最小的偏差为0.32%。这结果与理论相一致，表明该设计方法的合理。

3.2 主要几何参数对结构性能影响规律分析

鱼形仿生柔性翼的主要参数包括外板厚度t1、内板厚度t2、隔板角度θ。它们决定这鱼形仿生柔性翼的摆动程度，其因素水平如表2所示。采用正交表L25(53)设计试验，试验方案和结果如表3所示。

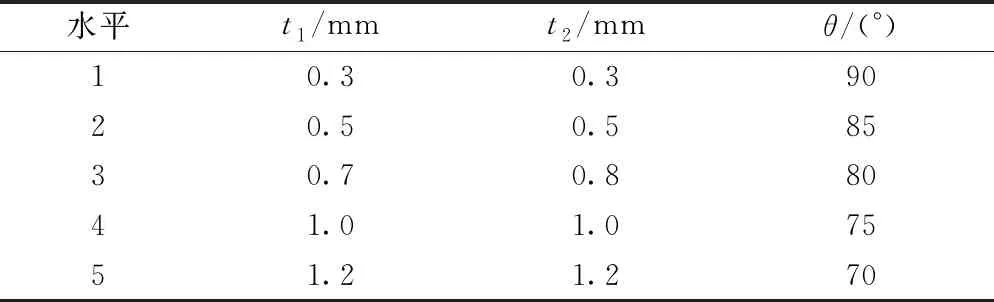
表2 正交试验各因素水平表

表3 正交试验表

Minitab是一款现代质量管理统计软件[18]，作为一款优异的正交实验后处理软件，可以很有效地分析各因素各水平对性能指标的均值主效应、信噪比主效应和贡献率。其中，均值主效应的幅值越大，对性能指标影响越重要；信噪比为质量特征值的均值与样本方差比值的平方，反映稳健设计中性能指标稳健程度，其数值越大，系统波动越小，越稳定；贡献率为各因素的均值主效应幅值占整体幅值的百分比，可衡量各因素对性能指标影响的程度。运用Minitab软件对正交试验结果进行统计分析，可获得各因素各水平对驱动载荷和振动幅值的信噪比主效应和贡献率，如图8、表4所示。

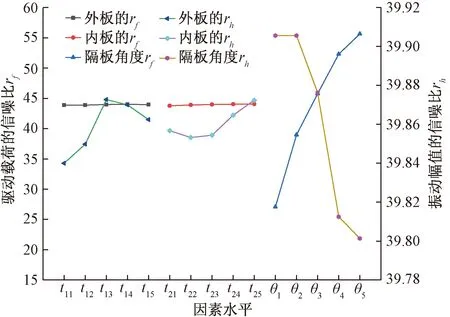
图8 驱动载荷与振动幅值正交实验信噪比主效应

表4 各因素水平对驱动载荷与振动幅值的贡献率

由图8和表4可以看出，隔板角度θ、内板厚度t2、外板厚度t1对驱动载荷的影响数值分别为28.56%、0.3%、0.13%,可以看出影响程度在依次减弱；其中隔板角度θ对驱动载荷的贡献率为28.56%,是三者里面的主导因素。隔板角度θ的值越大，驱动载荷就越大；相比而言外板厚度t1、内板厚度t2对驱动载荷的影响较小；并且可以得出主次因素顺序的最优组合为θ5-t21-t15，以获得最大驱动载荷。

由图8和表4还可以看出，隔板角度θ、外板厚度t1、内板厚度t2对振动幅值的影响数值分别为0.1%、0.02%、0.01%,可以看出影响程度在依次减弱；其中隔板角度θ对振动幅值的贡献率为0.1%,是三者里面的主导因素。隔板角度θ对驱动载荷越大，振动幅值就越小；相比较而言外板厚度t1、内板厚度t2对驱动载荷的影响较小，外板厚度t1的影响先增大再减小，而内板厚度t2的影响先减小在增大；这就可以得出主次因素顺序的最优组合为θ1-t13-t25，以获得最大振动幅值。

驱动载荷与振动幅值的最优组合并不相同，需要综合考虑二者的指标，最终获得影响因素的排序和优异组合。仿生柔性翼在实际设计中优先考虑其是否能承受摆动受到的压力，即优先考虑其驱动载荷。隔板角度θ在对驱动载荷和振动幅值的影响中均为主导因素，但是对驱动载荷的影响程度为28.56%,对振动幅值的影响程度为0.1%,相比而言对驱动载荷的影响程度更大，所以可以在不考虑对振动幅值的影响下，提高隔板角度θ，来提高驱动载荷。因此可将θ作为影响驱动载荷和振动幅值综合指标的第一主导因素。因而可以选择θ5作为试验对象的最佳隔板角度。内板厚度t2对驱动载荷和振动幅值的影响是次要因素,对驱动载荷的影响程度为0.3%,对振动幅值的影响程度为0.02%,相比而言对驱动载荷的影响程度更大，所以可以在不考虑对振动幅值的影响下，优先选择对驱动载荷更好的方案。因而选择t21作为试验对象的最佳内板厚度。

由图9所示，在不同的外板厚度下，对振动幅值的影响微弱,最大偏差为0.03%，但是对驱动载荷有着区别性影响。考虑到304不锈钢所能承受的弹性应力，选用t13作为外板的最优厚度。并且由图10可以验证在隔板角度、内板厚度不变的情况下，t13所达到的最大振幅姿态是最好的。因此选用了θ5-t13-t21作为实验对象的最佳组合。

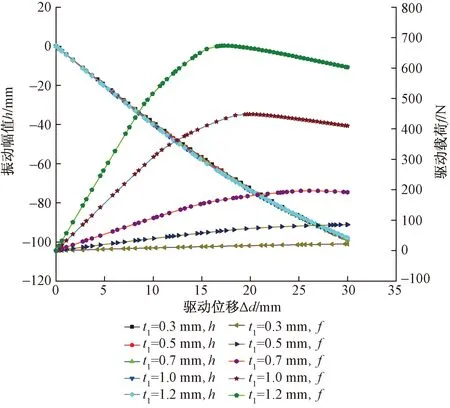
图9 驱动载荷及振动幅值与驱动位移的变化曲线

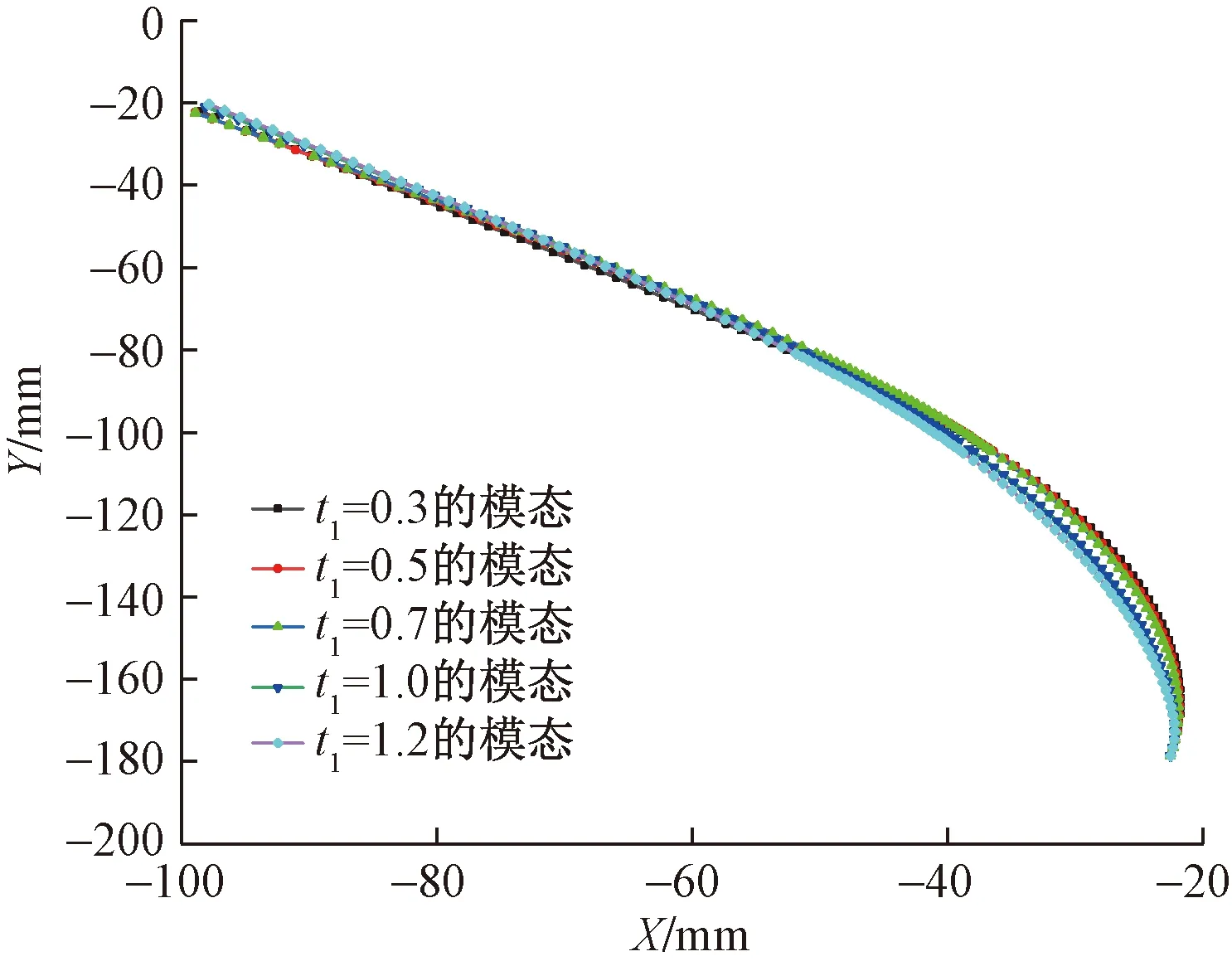
图10 最大振动幅值姿态对比

3.3 周期振动性能分析

在ABAQUS中设置150个周期性条件，设置驱动位移为10 mm和20 mm，得出两者的鱼形仿生柔性翼的滞回曲线。滞回曲线是指在反复作用下结构的载荷-变形曲线。主要是在反映结构在反复受力过程中的变形特征、刚度退化即能量消耗，即滞回曲线的性能。

图11所示为鱼形仿生柔性翼在周期性条件下驱动载荷f-驱动位移Δd曲线(Δd以往上推为正，往回拉为负)。图11(a)所示，驱动位移为10 mm的滞回曲线呈近似直线，驱动位移跟驱动载荷的乘积，即线条围成的面积就是所消耗的能量。由图11(a)可知，线条围成面积非常小，正向载荷最大偏差Δf1=0.794 N,负向载荷最大偏差为Δf2=5.296 1 N,两个偏差都很小，这就反映驱动位移为10 mm时，振动都在弹性阶段以内，低消耗。当驱动位移为20 mm时，如图11(b)所示，曲线呈梭形，且关于原点大致对称，该形状的曲线有利于在周期性位移下的耗能。从图11(b)可以看出正向载荷最大偏差Δf1=18.421 N，负向载荷最大偏差Δf2=24.503 N,两个偏差都较小，这就反映了整个结构塑性变形能力很强，具有很强的抗震性和耗能能力。但是驱动载荷间相差范围略大，这就会发生塑性变形，导致材料损坏。

图11 驱动载荷滞回曲线

如图12所示，当驱动位移为10 mm时，取第10、50、100、130、150周期的滞回曲线，5条曲线几乎完全重合，并将这5个周期摆动的最大幅值记录如表5所示，可发现这5个值两两间最大误差为1.74%。这就可以得出初始振动幅值小些，可以保证后续振动幅值的一致性。

图12 驱动位移为10 mm的各时刻驱动载荷滞回曲线

表5 各周期时刻振动幅值

4 结论

对锦鲤下躯干柔性翼模型进行设计研究，并分析了模型各参数对性能的关系，并将仿真结果与实验结果进行对比，得出如下结论。

(1)锦鲤的躯干运动姿态与设计的鱼形仿生柔性翼运动姿态相吻合；作为优选，外板厚度取0.7 mm，内板厚度取0.3 mm，隔板角度取75°。

(2)鱼形仿生柔性翼的临界屈曲载荷远大于驱动载荷，即驱动载荷占结构设计的主要因素，鱼形仿生柔性翼的变形发生在底部受力处。

(3)鱼形仿生柔性翼的主要参数对驱动载荷影响的主次顺序为：隔板角度、内板厚度、外板厚度，可以通过调节隔板角度来提高驱动载荷的极限，内板厚度对驱动载荷的影响较小，外板厚度对驱动载荷的影响很小；对振动幅值影响的主次顺序为：隔板角度、外板厚度、内板厚度，可以通过调节隔板角度来提高振动幅值的极限，外板厚度对振动幅值的影响较小，内板厚度对振动幅值的影响很小。但是相比较而言隔板角度对驱动载荷的影响更大，因此最好可以通过调节外板厚度来提高振动幅值极限，以确保不会两者相互影响，难以调节。

(4)基于正交试验的θ5(75°)-t25(1.2 mm)-t15(1.2 mm)、θ1(90°)-t13(0.7 mm)-t25(1.2 mm)、θ5(75°)-t13(0.7 mm)-t21(0.3 mm)，可为鱼形仿生柔性翼设计提供参考依据，避免参数的盲选和反复试验。

(5)该结构具有良好的回塑性，初始振幅小些，并多次做往复运动，后续的振动幅值保持一致，最大误差仅为1.74%。