拟广义加权引致OWA算子及其应用*

徐迎军

(曲阜师范大学经济学院，山东 日照 276826)

引言

在决策分析中一个重要的问题是用集结算子把不同信息来源的多个信息集结成为一个综合信息，因此对集结算子的研究引起了众多研究者的极大兴趣[1-3].Harsanyi提出了加权平均(Weighted Averaging, WA)算子，此后得到了广泛应用[4].Yager创新性地提出了OWA(Ordered Weighted Averaging, OWA)算子[5].Xu和Da把几何平均算子与OWA算子集成到一起，提出了有序加权几何平均(Ordered Weighted Geometric，OWG)算子[6]，此算子有广泛应用[7].Fodor等把拟算术平均算子与OWA算子进行了集成，提出了拟算术OWA(Quasi OWA, Q-OWA)算子[8].

Mitchell和Estrakh提出了一修正的OWA算子，其元素的排序是依据元素的某函数值[9].Yager和Filev基于Mitchell和Estrakh的顺序引致思想对OWA进行了进一步扩展，提出了IOWA[10].Chiclana等提出了重要性IOWA(Importance IOWA, I-IOWA)算子、一致性IOWA(Consistency IOWA, C-IOWA)算子和偏好IOWA(Preference IOWA, P-IOWA)算子用来集结模糊偏好关系[11].Merigo和Casanovas把DS(Dempster Shafer)证据理论引入IOWA算子，提出了信度结构IOWA(Belief Structures IOWA, BS-IOWA)算子[12].

Yager把广义平均的思想引入OWA，提出了广义有序加权平均(Generalized Ordered Weighted Averaging，GOWA)算子[13].Merigo和Gil-Lafuente把GOWA和IOWA融合到一起，提出了引致广义OWA算子(Induced Generalized OWA, IGOWA)[14]和拟IOWA(Quasi IOWA, Q-IOWA)算子.Merigo等基于充分性参数对IGOWA进行了扩展[15].基于我们对分析问题的兴趣，我们可以给予不同算子不同的重要性.为解决此问题，Merigó提出了IOWAWA算子，把IOWA算子和WA算子统一到一个公式中，考虑到了不同算子的重要性[16].Merigo等考虑到概率算子、WA算子和OWA算子的重要性，把它们统一到一个引致概率有序加权平均加权平均(Induced Probabilistic Ordered Weighted Averaging-Weighted Averaging)算子中[17].

Aggarmal引入一参数来控制补偿度，提出了补偿加权平均(Compensative Weighted Averaging, CWA)算子[18].Aggarwal把广义平均思想引入CWA算子，提出了广义补偿加权平均(Generalized Compensative Weighted Averaging, GCWA)算子，并把GCWA和OWA融合为广义补偿有序加权平均(Generalized Compensative Ordered Weighted Averaging, GCOWA)算子，把GCWA和IOWA融合为广义补偿引致有序加权平均(Generalized Conpensative Induced Ordered Weighted Averaging, GCIOWA)算子[19].Aggarwal对IOWA进行了扩展，基本思想是，把引致顺序变量信息与加权向量进行融合，得到新的加权向量，充分利用了信息，提出了加权引致有序加权平均(Weighted Induced OWA, WIOWA)算子[20].本文把拟算术平均算子有机融合进WIOWA算子，提出了更具广泛性的拟广义加权引致有序加权平均(Quasi Generalized Weighted Induced OWA, QGWIOWA)算子.并通过具体例子来验证了新算子的可行性和有效性.

1 预备知识

在这一部分，简要介绍OWA算子、IOWA算子和广义OWA算子等.Yager创新性地提出了OWA算子，此算子为一广泛的算子族，包括算术平均、最大算子以及最小算子等[5].

定义1n维OWA算子为一映射，OWA：Rn→R，W=(w1,…,wn)为其伴随n维权重向量，满足权重向量分量之和为1，且均为非负分量：

(1)

(a1,a2,…,an)为被集结元素向量，(b1,b2,…,bn)为把(a1,a2,…,an)的分量从大到小重排之后的数据向量.可以对重排操作进行扩展，即区分从大到小和从小到大，则可把OWA算子区分为下降OWA和上升OWA.OWA算子具有单调性、有界性、幂等性和可交换性等性质[5].

OWA算子中一个重要的步骤是对被集结元素进行重排序，而在此过程中OWA算子只利用了被集结算子本身的信息，忽略了其他重要信息，比如决策者的判断一致性或者经验的丰富程度等信息，Yager和Filev基于Mitchell和Estrakh的顺序引致思想[9]对OWA进行了进一步扩展，提出了IOWA[10].

定义2n维IOWA算子为一映射，IOWA：Rn→R，W=(w1,…,wn)为其伴随n维权重向量，满足权重向量分量之和为1，且均为非负分量.(a1,a2,…,an)为被集结元素向量，每一个被集结元素ai均有一个相应的顺序引致元素ui，根据相应的ui(i=1,…,n)对所有被集结元素ai(i=1,…,n)按照从大到小顺序进行排列，得到重排之后的被集结元素向量(b1,b2,…,bn)，然后利用权重向量对(b1,b2,…,bn)用下面的公式进行集结：

(2)

IOWA算子也具有单调性、有界性、幂等性和可交换性等性质.Yager把广义平均思想融合进OWA算子，利用一参数来控制被集结元素的被集结强度，对OWA算子进行了推广，提出了下面的GOWA算子[7].

定义3 (广义OWA算子)算子M:Rn→R称为n维GOWA算子，如果

(3)

其中W=(w1,…,wn)为其伴随n维权重向量，满足权重向量分量之和为1，且均为非负分量；λ为一参数，满足λ∈[-∞,∞]；bj是第j个最大的ai.

2 拟广义加权引致OWA算子及其性质

本文把WIOWA算子进行了推广，提出了QGWIOWA算子如下.

定义4[21](WIOWA) WIOWA算子是一个映射，WIOWA:Rn→R.集结数据为(a1,…,an)，相关联的加权向量为W=(w1,…,wn)，满足wi∈[0,1],i=1,…,n，且∑iwi=1.顺序引致向量为u=(u1,…,un).集结数据ai的顺序由与其相关联的变量ui来导出.即根据与ai相关联的引致变量ui的值对ai进行排序，设得到的排序后的数据序列为Bu=(b1,b2,…,bn).可表示如下：

WIOWA(,…,)=WTBu

(4)

WIOWA集结需要两个步骤.第一步，通过把与ai相关联的引致变量ui进行排序，得到重排后的数据序列Bu=(b1,b2,…,bn)，其中bi是具有第i大的引致变量值ui的ai.重排后的集结对象为(,…,).接着，vi(i=1,…,n)与wi∈W(i=1,…,n)共同产生加权向量：

(5)

(6)

因此，顺序引致变量值vi(i=1,…,n)除了导出原始数据(a1,…,an)在集结中的顺序外，还被用来产生集结权重.就像在IOWA算子中一样，顺序引致变量可能是专家的信心、意见一致性、偏好等或其他性质.下面把WIOWA进行推广，得到QGWIOWA算子.

定义5 (QGWIOWA)n维QGWIOWA算子是一个映射：QGWIOWA：Rn→R：

(7)

(,…,)是被集结的数据对，a1,…,an是被集结的数据元素，u1,…,un分别为与a1,…,an相对应的顺序引致数据.关联权重向量是W=(w1,…,wn)，满足wi∈[0,1],i=1,…,n，且∑iwi=1.(v1,…,vn)为(u1,…,un)按照由大到小顺序重排后的顺序引致变量.f:R→R为一严格单调递增函数.g:R→R为一严格单调函数.

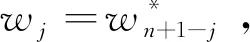
接下来讨论QGWIOWA的一些性质，包括单调性、有界性、幂等性和可交换性等.

定理1(单调性) 令集结数据α=(a1,…,an)，β=(b1,…,bn)，满足ai≤bi对∀i成立.相关联的加权向量为W=(w1,…,wn)，满足wi∈[0,1],i=1,…,n，且∑iwi=1.顺序引致向量为u=(u1,…,un)，那么，

QGWIOWA(,,…,)≤

QGWIOWA(,,…,)

(8)

证明由(8)得到，

其中(c1,…,cn)是(a1,…,an)根据顺序引致变量(u1,…,un)按照降序重排得到的序列，(d1,…,dn)是(b1,…,bn)根据顺序引致变量(u1,…,un)按照降序重排得到的序列.因为ai≤bi对∀i成立，所以，ci≤di对∀i成立.所以，

QGWIOWA(,…,)≤QGWIOWA(,…,).

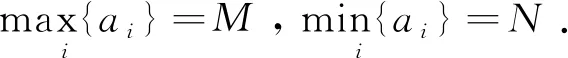
N≤QGWIOWA(,…,)≤M

(9)

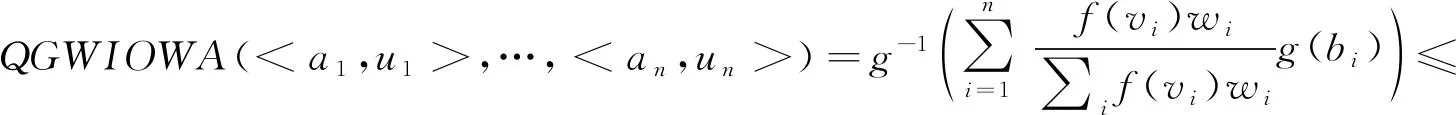
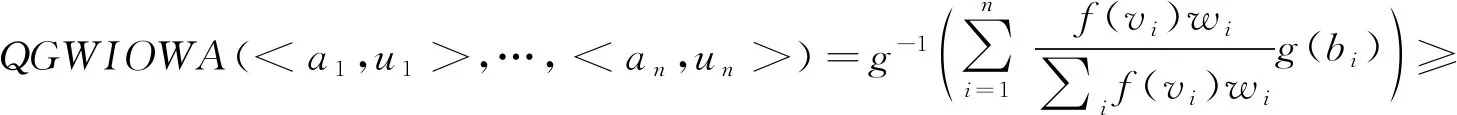
因此，N≤QGWIOWA(,…,)≤M.

定理3(幂等性) 如果对∀i，有ai=a,则：

QGWIOWA(,…,)=a

(10)

证明根据与ai相关联的引致变量ui的值对ai进行排序，设排序后的数据序列为Bu=(b1,b2,…,bn).因为对∀i，有ai=a，所以，对∀i，bi=a.有

定理4(置换不变性) 设(,…,)是(,…,)的任何一种重排列.那么

QGWIOWA(,…,)=QGWIOWA(,…,)

(11)

证明根据与ai相关联的引致变量ui的值对ai进行排序，设排序后的数据序列为(,…,).根据与ci相关联的引致变量mi的值对ci进行排序，设排序后的数据序列为(,…,).对∀i，di=bi，ni=vi，有

定理得证.

QGWIOWA算子是一族非常广义的算子，它包含了许多重要的算子.当f(x)=g(x)=x时，QGWIOWA算子退化为WIOWA算子.当f(x)≡1，且g(x)≡xλ时，QGWIOWA算子退化为GOWA算子.

3 决策应用

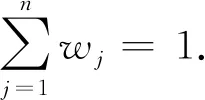
Step 1：建立决策矩阵；

Step 2：利用QGWIOWA算子得到方案综合属性值；

Step 3：根据综合属性值对方案进行排序.

例1 现对国内四家航空公司X={x1,x2,x3,x4}的服务质量进行评价[21].评价指标为：c1为定售票服务，c2为登记程序，c3为客舱服务，c4为响应性.指标权重向量确定为(0.15,0.25,0.35,0.25).经过专家评估建立决策矩阵M=(aij)44.根据专家给出的决策矩阵，对四家航空公司的服务质量进行评价.

Step 1：由专家给出关于四家航空公司服务质量的决策矩阵见表1(评分为10分制)：

表1 专家关于四家航空公司的属性评价决策矩阵

Step 2：由QGWIOWA算子得到各个方案的综合属性值如下：

为简单起见，在此假设对于四家航空公司，ui=ai，i=1,2,3,4，即顺序引致变量值与属性评价值是一致的.且令f(x)=2x，g(x)=3x+1.

x1=31.162 76；x2=27.879 23；x3=30.156 86；x4=29.961 45.

Step 3：根据方案的综合得分值，其优劣排序为：

x1≻x3≻x4≻x2.即第一家航空公司x1是最优的.

为了考察不同的函数对集成结果的影响，分别选取几种情形：

1)f(x)=2x，g(x)=3x+1；

2)f(x)=x2，g(x)=3x2+1；

3)f(x)=x3，g(x)=3x3+1.

本例中，所有评价值都是正值，在自变量取正值时，三种情况下的函数都是严格单调函数.通过QGWIOWA算子计算出方案综合属性值，将综合属性值和排序结果列入表2.

表2 方案综合属性值和方案排序

由表2中计算结果可以看到：当f(x)和g(x)取值不同时，排序结果有差异，可见在实际使用QGWIOWA算子时，应根据需要，选择合适的函数f(x)和g(x).

5 结论

把WIOWA推广为QGWIOWA算子，证明了QGWIOWA算子的幂等性、单调性、有界性等性质.提出了基于QGWIOWA算子的决策方法，并通过具体例子验证了决策方法的有效性.本文研究结果丰富了OWA算子相关理论.

可以把几何平均的思想融入QGWIOWA，提出几何版的QGWIOWA算子.另外，作为模糊集的推广的直觉模糊集，可以从支持、反对和中立三个方面来刻画对某问题的态度，能更好地反应现实情境，受到了学者们的关注.然后，学者们在利用直觉模糊集对方案进行评价时，容易出现隶属度和非隶属度的和大于1的情形，为有效处理这种情况，Yager提出了毕达哥拉斯模糊集，允许隶属度和非隶属度的和大于1，但限制其平方和不大于1[22].把QGWIOWA算子推广到毕达哥拉斯模糊集环境中是一个有意义的研究主题.