盾构隧道施工对柔性地下管线的影响预测及分析*
2021-11-22宋建学郝凌霄张澄玄
宋建学,郝凌霄,师 刚,张澄玄
(1.郑州大学土木工程学院,河南 郑州 450003; 2.上海同岩土木工程科技股份有限公司,上海 200092)
0 引言
盾构法施工会打破原有土层的应力平衡,不可避免地引起周围土体变形,严重的可能导致土体塌方[1],这种影响在双线盾构施工过程中尤为明显。城市地下管线在城市中起着极其重要的作用。地下管线系统一旦发生事故,不仅会造成巨大的经济损失,同时也会产生社会影响。因此,研究地铁隧道施工对邻近地下管线的影响,预测影响范围和变形幅度等具体指标具有实际意义。目前,国内外关于盾构施工引起管线变形的研究方法主要有数值分析法[2]和解析法[3-4]。王忠昶等[2]利用FLAC3D建立隧道-土体-管线共同作用模型,对盾构施工所导致的管线变形和应力进行模拟,认为双线隧道施工产生的地表沉降槽不符合叠加理论。Klar等[3]利用边界积分法研究了隧道施工对既有管线的影响问题,提出了计算最大弯矩和接头转角的标准化解析方法,认为管道变形取决于管道相对于土的刚度和相对于隧道中心线的位置。魏纲等[4]基于能量法,结合土体沉降建立能量变分方程,推导出双线盾构施工导致管线沉降的计算公式,认为土体损失率是造成管线沉降的重要因素。综上所述,目前关于盾构施工对管线影响的研究虽然很多,但并无管线接头张开值与隧道盾构沉降结合来进行研究。
本文以管线接头允许张开值为指标,建立了盾构施工上方柔性市政管线安全状态评估方法,并基于工程实例研究了地铁隧道埋深、平距等对市政管线的影响规律。
1 地下管线破坏模式和评价指标
地下管线的破坏模式主要分为以下两种[5]:①接头相对变形破坏;②管段应力破坏,如图1所示。当管线为柔性接口时,容易因为接头的相对变形而发生破坏;当管线为刚性接口时,容易因为管段的应力过大而发生强度破坏。

图1 地下管线破坏模式
以往的岩土工程施工往往通过监测管线的沉降差、管线接头张开值以及管线应力等指标来判断管线的安全性[6-8]。实际工程中,通常选取管线沉降梯度和接头张开值作为柔性管线状态评价指标,选取管线应力作为刚性管线的状态评价指标,以此为依据分析管线安全性。根据实际工程调查,主要研究种类繁多、数量庞大的柔性管线接头破坏模式。
如图2所示,管线地基沉降曲率半径为R,管线管节长为Ls,管线外径为D,管线接头张开值为Δ,根据几何关系,可得[9]:
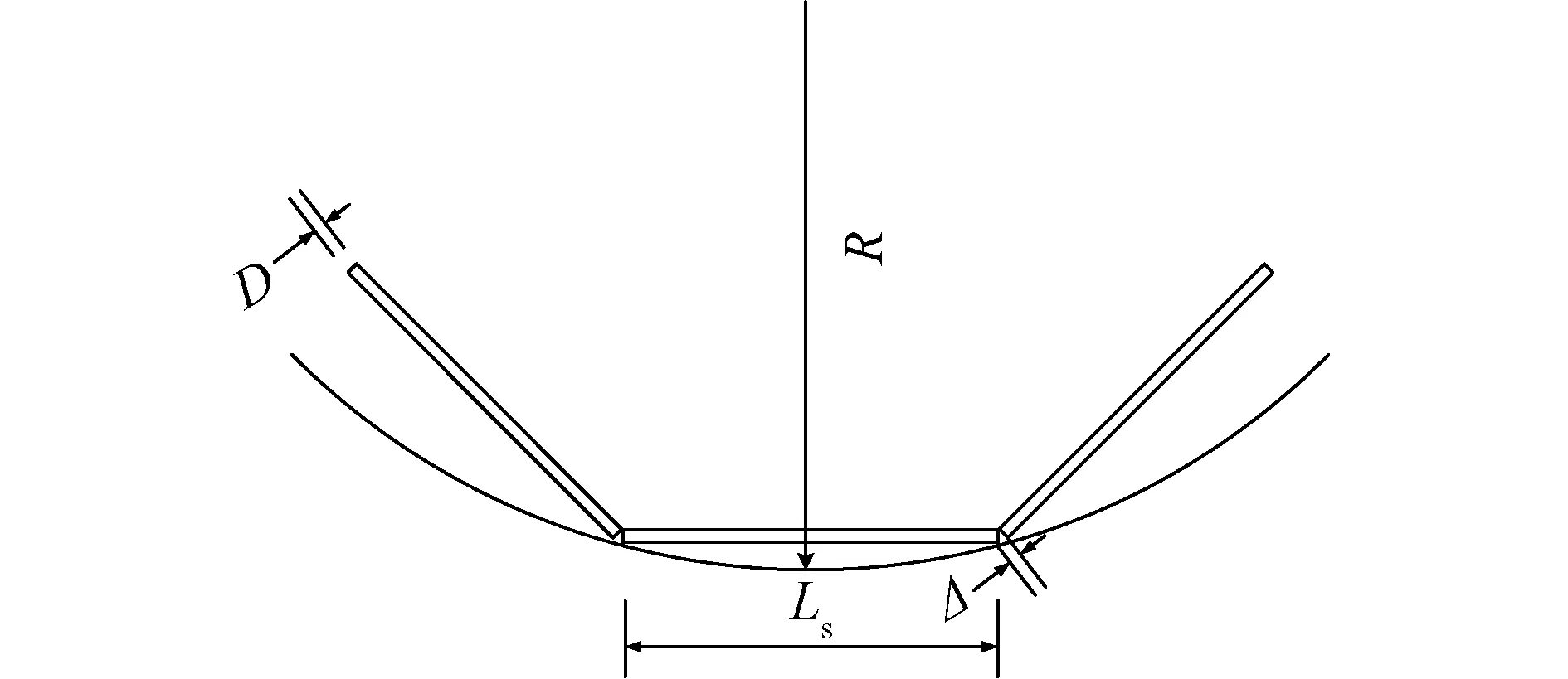
图2 管线接头张开值与管线曲率半径关系
(1)
若已知管线接头的允许张开值[Δ],则可利用式(1),确定线路允许曲率为:
(2)
设图2中沉降曲线为y(x),可得曲线曲率1/R为:
(3)
若能得到盾构施工过程中地下管线的沉降曲线,则可以利用式(3)求出管线接头曲率,联立式(2)得到:
(4)
由式(4)可知,当已知管道的单节长度Ls、直径D和沉降曲线y(x)后,同时确定了管线的允许张开值,便可以判定管线是否破坏。
2 双线盾构隧道土体沉降
Peck基于试验提出单线盾构引起的横断面沉降估算公式为:
(5)
(6)
式中:x为距隧道轴线横向水平距离;S(x)为x位置处的地面沉降量;Smax为隧道轴线上方最大地面沉降量;i为地面沉降槽宽度系数, 为从沉降曲线对称中心到曲线拐点的距离;Vloss为单位长度土体损失量,Vloss=πR2η;R为隧道开挖半径;η为土体损失率。
很多学者对Peck公式进行了更进一步的补充研究,陈春来等[10]提出双线盾构施工引起的三维土体沉降计算公式:
(7)
式中:Smaxf和Smaxl为先行隧道和后行隧道轴线上方最大地面沉降;y为盾构掘进方向;z为离地面竖向距离;L为两隧道中心距离;if和il为先行隧道和后行隧道的地面沉降槽宽度系数;ηf和ηl为先行隧道和后行隧道的土体损失率。双线平行盾构相对位置如图3所示。
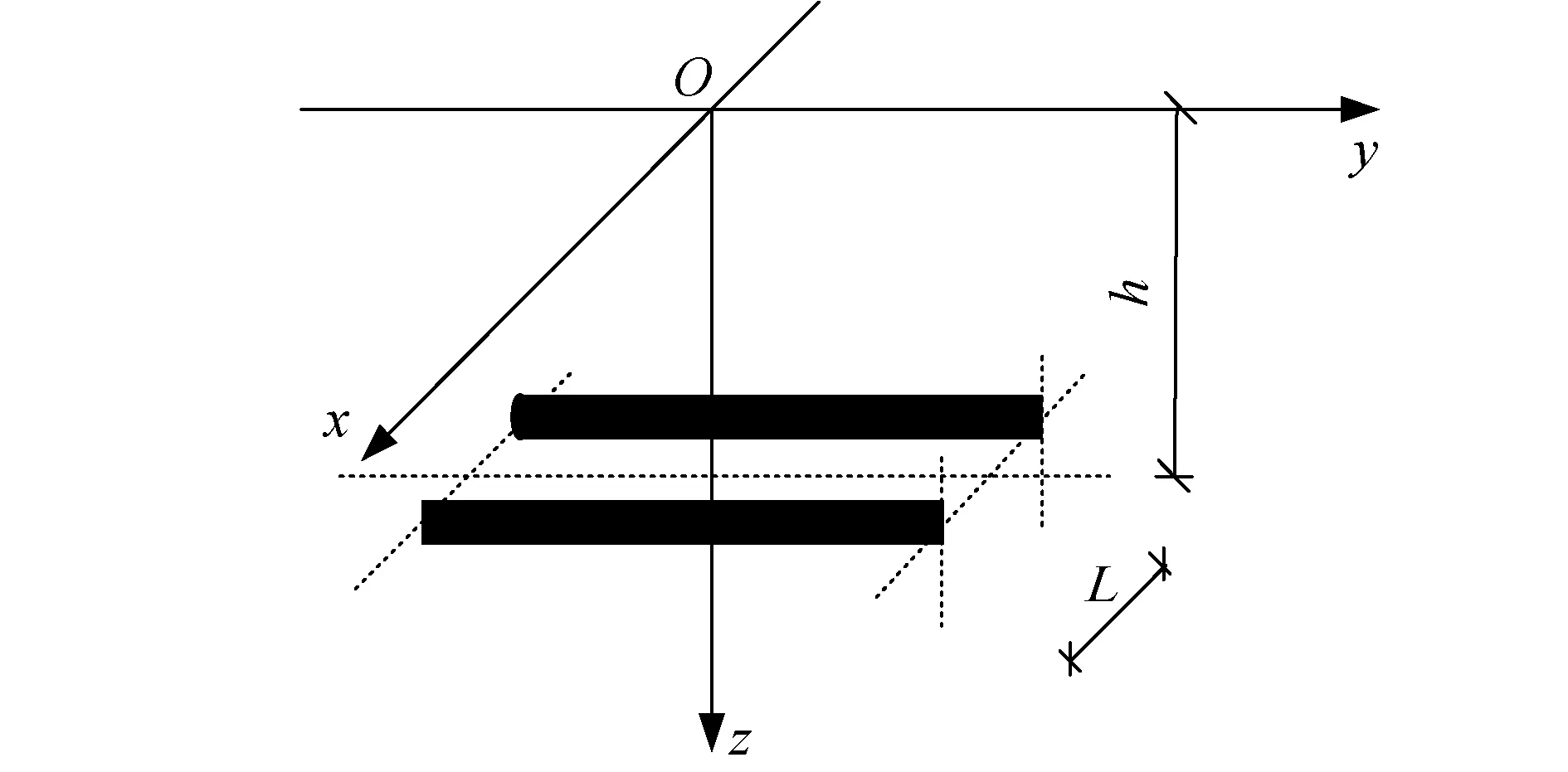
图3 双线平行盾构相对位置示意
3 双线盾构隧道施工对管道的影响
管道与盾构隧道空间位置关系最基本的可以分为两种,一种是盾构方向与管道正交,如图4所示;另一种为盾构方向与管道方向平行。所研究的为二者相互垂直条件下的影响,并假定管道变形与周围土体变形完全同步,即以土体变形代替管线变形。
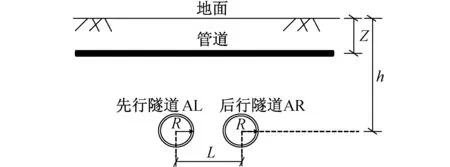
图4 隧道下穿管道示意

(8)
结合式(4),可以得到计算张开值的表达式:
Δ=LsDP
(9)
当已知管线允许张开值时,便可通过式(9)对管线是否安全进行判断。
当管线是柔性管线时,管线的变形状态用张开值表示。当管线的接头张开值小于允许张开值时,管道处于安全状态,否则将产生不同程度的破坏。骆建军[11]等对国内有代表性的3种柔性管道做了弯曲和拉伸试验,所得接口张开值如表1所示。

表1 接头张开值 mm
彭立敏等[12]经过进一步的研究和工程实践,并参考近些年来的一些试验成果,建议了更严格的张开值控制指标,如表2所示。
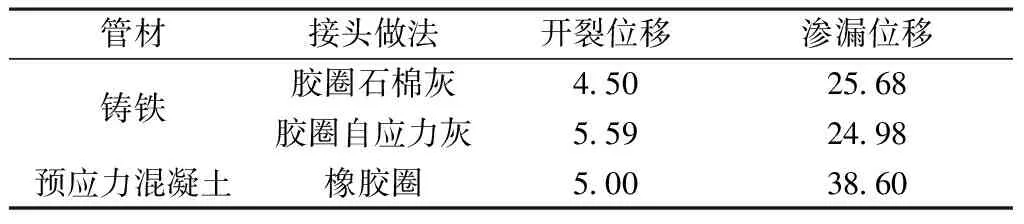
表2 接头张开值 mm
为了安全起见,本文针对常见市政污水管道取接头张开容许值5mm。
4 算例及分析
4.1 隧道设计深度
针对郑州典型地质单元郑东新区,结合郑东新区地铁4号线农业东路站—如意湖北站区间施工的沉降观测数据进行回归分析。由于篇幅有限,仅选取其中比较具有代表性的断面DB-2,并采用式(7)对其土体损失率和沉降槽宽度系数进行反分析,结果如图5所示。

图5 断面DB-2横向地面沉降曲线
拟合曲线表达式为:
S(x)=42.82e-0.007 8(x+10)2+47.19e-0.011 1(x-10)2
(10)
通过数据反分析,得出土体损失率ηf=1.2%,ηl=1.3%;地表沉降槽宽度系数if=6.7m,il=8m。为便于后续分析,忽略先行隧道施工对后行隧道的影响,取if=il=8m,ηf=ηl=1.3%。
根据郑东新区工程实例调查情况,某直径600mm污水管道南北向布设,南浅北深,埋深范围为5~8m,管线总长度1.2km,管道每节段长4m,采用国标Ⅱ级钢筋混凝土管,承插式橡胶圈接口。地铁线路将在不同位置正穿该污水干道,计划设计两隧道轴线间距12m,需要确定地铁隧道合理埋深。根据不同隧道埋深,由式(9)计算并绘制出污水管道埋深8m处的计算张开值曲线,并以5mm为临界值,作为判别管线是否安全的因素,如图6所示。

图6 计算张开值曲线
由图6可以看出,当隧道轴线埋深为17~19m时,计算张开值有大于5mm的情况;而轴线深度为20m时,计算张开值均小于5mm。详细计算表明,污水管线埋深8m时地铁隧道最小埋深为19.5m。
管道埋深在3~10m时,根据不同的双线隧道水平间距,计算确定隧道最小埋深,如表3所示。

表3 不同隧道间距下的最小设计深度
4.2 沉降值与计算张开值
为了更好地研究沉降值与市政管线接头计算张开值的变化规律,以隧道埋深24m为例,各参数同4.1节,计算L=10~32m时,左、右线隧道轴线处(Al和Ar处,基于对称关系,下文统一以Al表述)和地铁线路中轴线(为便于描述,下文统一以Am表示)在地下10m处的沉降值与张开值(张开值统一取绝对值),结果如图7,8所示。
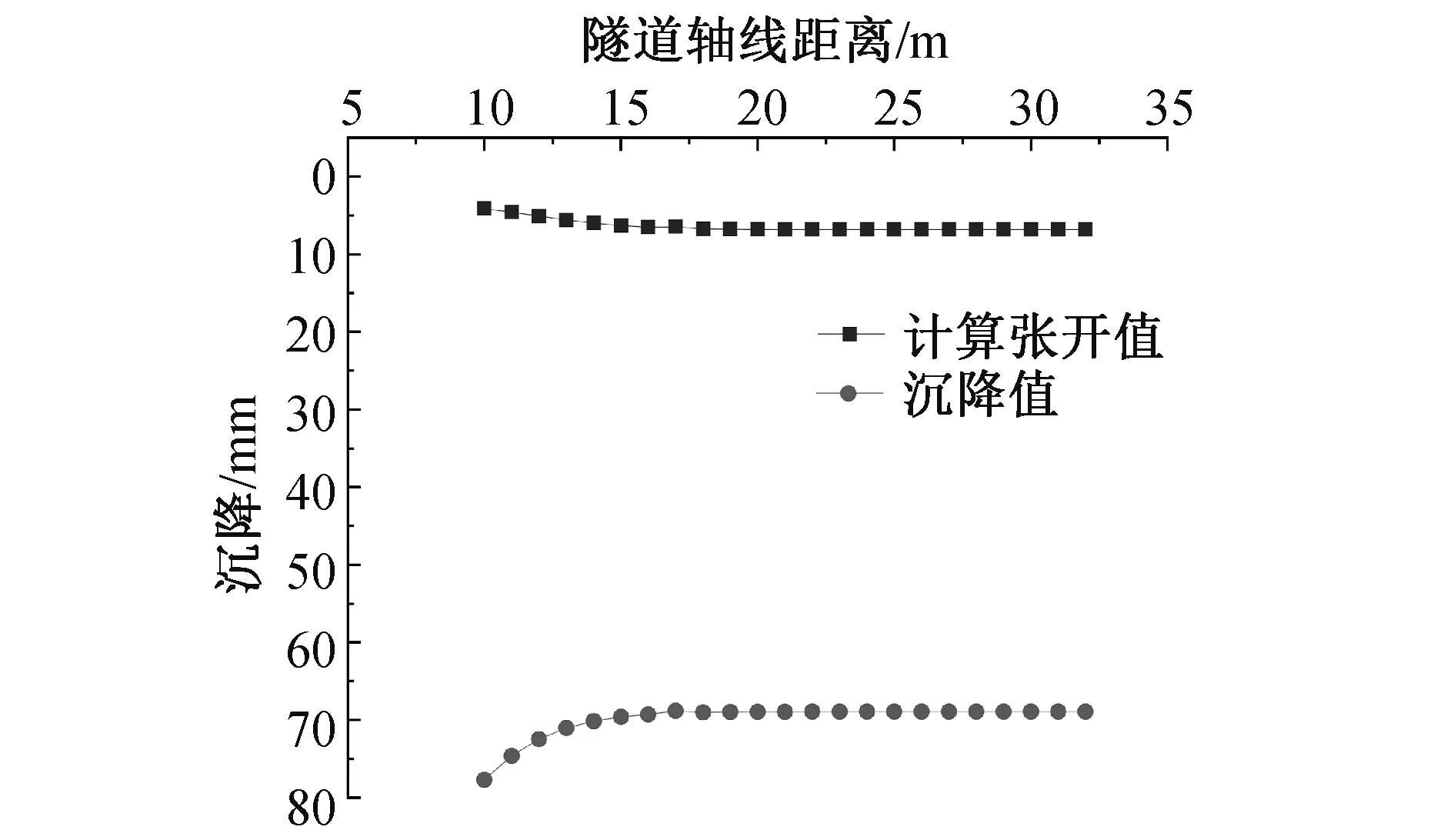
图7 不同隧道间距条件下Al处的计算张开值与沉降值
由图7可知,对比计算张开值与沉降值的变化可以发现,在L=10~32m范围内,随着L的增大,Al处的沉降值逐渐减小,此处的沉降变化为单调递减;然而计算张开值变化不明显,在L=17m时张开值达到最大值,然后基本保持不变。
由图8可知,对比计算张开值与沉降值的变化可以发现,随着L的增大,Am处的沉降呈单调减小;而计算张开值则呈勺形分布,当L为17m时,计算张开值达到最大。

图8 不同隧道间距条件下Am处的计算张开值与沉降值
分析认为:当两隧道距离接近时,各自产生的沉降曲线会互相叠加,使得Am和Al处的沉降量增加;当L超过某一特定值时,两隧道间的相互影响逐渐趋于零,产生的最大沉降值逐渐趋于固定值。差异沉降随两隧道间距变化不明显,而在L为17m时出现峰值。
由式(7)所计算出的沉降值比实际沉降偏大,这是因为盾构过程中盾壳摩擦力和正面附加应力会导致土体产生隆起效应,而此计算方法并未考虑该因素,为数值计算结果,仅供理论分析、对比使用。
4.3 沉降曲线形状分析
Peck公式和修正Peck公式提出的双洞盾构隧道施工产生的土体变形大体可以分为两类,如图9所示,一类为V形,另一类为W形。
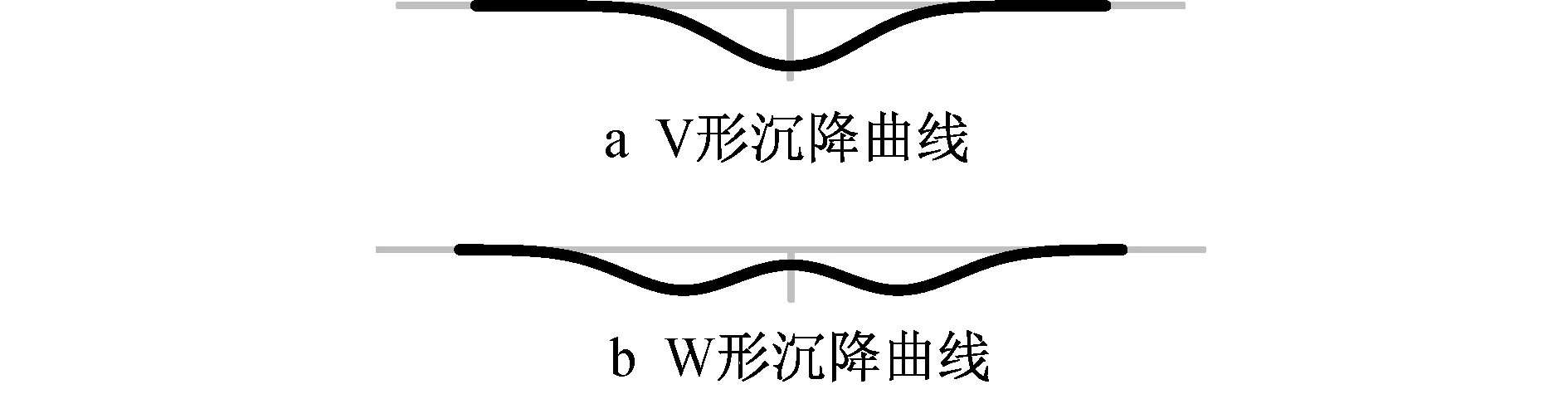
图9 沉降曲线类型
图9中,两类曲线均以y轴向下为正。通过观察可以发现,V形曲线在x=0处为凸曲线,而W形曲线在x=0处为凹曲线。根据数学原理可知,V形曲线在x=0处的二阶导数应为负值,W形曲线在x=0处二阶导数应为正值。结合式( 9)可知,计算张开值的正负与二阶导数正负相同。因此,实际工程中可以根据计算张开值的正负,对沉降曲线凹凸特性进行划分,进而判断变形类型。
以地铁隧道轴线深度24m为例,假定计算参数同4.1节,研究两隧道轴线间距L变化时,地表下3m处的沉降值变化,结果如图10所示;Am处计算张开值的变化如图11所示。

图10 双线地铁隧道平距L与沉降分布

图11 计算张开值曲线
由图10可右,当L=8,14m时,沉降曲线呈V形;L=20,32m时,沉降曲线呈W形。由图11可知,当L=8~14m时,上方污水管道接头计算张开值为负,沉降曲线呈V形;当L>14m时,计算张开值为正,沉降曲线呈W形。此结果与沉降曲线结果相吻合,表明式(9)可应用于判断沉降曲线类型。
魏纲等[13]提出相对水平系数C=L/(h+R),且在文献[10]中指出C≤0.67时,地面沉降曲线符合正态分布;C>0.67时,地面沉降曲线不符合正态分布。由于此系数为地表沉降规律,不适用于地下管道,本文在此基础上对C进行修正,定义相对水平系数:
CZ=L/(h+R-Z)
(11)
式中:L为两隧道轴心间距;Z为市政管道轴心深度;h为地铁隧道轴线深度;R为地铁隧道半径。
现在研究CZ值的取值与沉降形态。前文研究表明,当L=14m时,沉降形态由V形转为W形。对柔性市政管线,其埋深大体范围为Z=3~10m,经分析可得,当CZ≤0.58时,管线沉降曲线呈V形;当Cz>0.58时,管线沉降曲线呈W形。
5 结语
1)根据郑州市郑东新区的具体情况,当污水管道埋深8m且地铁隧道轴线间距12m时,隧道轴线的安全深度最小值为19.5m。
2)当地铁隧道埋深确定后,随着两隧道间距的增大,上方市政管线的绝对沉降量单调减小,而管线接头张开值则呈勺形分布,当平距为17m时,张开值达到最大。
3)定义双线地铁隧道左右线水平距离系数,当CZ≤0.58时,上方市政管线沿轴线的沉降分布符合正态分布规律,呈V形分布;当CZ>0.58时,沉降曲线不符合正态分布规律,呈W形分布。
