双连拱地铁隧道衬砌结构地震动力响应特征

2021-11-22左红伟马甲宽

科学技术与工程 2021年30期

左红伟，马甲宽，任翔，白兰，喻畅

(1. 青岛理工大学土木工程学院，青岛 266033； 2. 长安大学建工学院，西安 710064；3. 西安长庆科技工程有限责任公司，西安 710054)

长期以来，人们一直认为地下结构在地震中具有较高安全性、稳定性，较少关注地震作用下地下结构的安全问题。然而，1995年日本阪神地震中多处地铁地下车站及其区间隧道产生严重破坏，之后相关研究人员开始逐渐把目光集中在地下工程抗震领域，对地下车站[1]、隧道[2-4]等地下结构的动力响应开展了系列研究。

朱正国等[5]通过对多元荷载耦合作用下立体交叉隧道的动力响应及安全性的定量分析，找出了不同隧道形式下衬砌结构断面的不同危险部位；何则干等[6]基于混凝土塑性损伤模型，采用三维非线性有限元模型模拟了山岭隧道洞口段结构的地震响应过程，分析了洞口结构横截面和纵向响应特征；郭正阳等[7]以天津Z2线盾构隧道工程为实例，分别计算了在安评波小震、中震和大震作用下的隧道内力和变形，为天津Z2盾构隧道抗震设计提供了参考。随着相关研究的不断开展，中国目前已经形成了《建筑抗震设计规范》《城市轨道交通结构抗震设计规范》等相关规范，对地铁地下结构的抗震设计进行了较为具体的规定，一定程度上保证了地下结构的安全性。

然而，目前能够体现黄土地质条件，指导黄土地区地铁地下结构抗震设计方法还几乎处于空白。随着西部大开发策略与“一带一路”倡议的不断推进，以西安为代表的典型黄土城市地下工程快速发展，黄土隧道工程日益增多，如何保证黄土地区隧道工程的抗震安全越来越受到相关研究人员关注。李世久等[8]研究了黄土隧道洞口段在地震作用下的动力响应特征、破坏过程和地震波在模型中的传递规律，分析了影响黄土隧道洞口段地震动力响应的主要因素；孙纬宇等[9]针对黄土边坡与隧道洞口段衬砌的相互作用问题，分析了以不同进洞高程进洞时黄土隧道洞口段衬砌的动力响应特征和洞口仰坡的动力稳定性；房军等[10]对宝兰客专黄土隧道洞口段在地震作用下的动力响应特征进行数值模拟研究，分析了边坡进洞高程对洞口段动力响应的影响；张晋东等[11]开展黄土隧道洞口段的大型振动台模型试验，对边坡不同高程位置处进洞的隧道洞口段坡-隧系统所表现出的震害特征和加速度响应特征进行了一定的研究。

综合黄土地区隧道地震响应方面研究发现，虽然目前已取得了一定成果[12-15]，然而关于黄土地区双连拱这种特殊隧道结构在地震作用下动力响应的研究却并不丰富，且主要集中于公路隧道。随着城市地下空间工程不断发展，双连拱隧道开始逐渐应用于城市地铁工程且数量日益增多，考虑到城市地铁双连拱隧道与公路连拱隧道的结构特点存在一定区别，同时城市地下工程的抗震安全性越来越被重视，开展黄土地区城市双连拱隧道地震动力响应特征研究，确保隧道在地震中的安全性就显得至关重要。

基于以上论述，现选取西安地铁5号线某区段双连拱隧道工程为研究对象，该连拱隧道中导洞与正洞开挖面积之比为1.4∶1，中隔墙受力特征更为复杂，是黄土地区典型地铁连拱隧道结构形式之一，具有较好研究意义。通过建立数值分析模型，对地震作用下地铁双连拱衬砌的动应力、动应变、加速度等动力响应特征开展研究，并与静力条件下的受力特征进行对比，分析结构的潜在风险，以期为类似双连拱隧道工程的地震安全性提供合理建议，降低潜在工程风险。

1 三维数值分析模型的建立

1.1 工程工况

受现场施工条件限制，西安地铁5号线某区段采用双连拱隧道结构形式，隧道宽度为11.60 m，高度为6.77 m；初衬、二衬、仰拱填充分别采用C25、C30、C25混凝土，其厚度分别为30、40、65 cm。场地土层主要包括人工填土、上更新统风积新黄土、残积古土壤、中更新统风积老黄土等，隧道上覆土体厚度约17.5 m，如图1所示。根据地勘资料，场地等效剪切波速为266.7 m/s，抗震设防烈度为8度，设计基本地震加速度值为0.2g(g为重力加速度)。

图1 双连拱隧道位置示意图Fig.1 The position diagram of double-arch tunnel

1.2 数值分析模型的建立

由于工程所在区段地层分布较为均匀，隧道断面保持不变且埋深变化较小，可以将其简化为平面应变问题。通过有限元建立二维分析模型，对参数相近土层进行合并，混凝土动弹模取静弹模的1.3倍[16]，主要土层及衬砌物理参数如表1所示。土体采用弹塑性本构模型(M-C屈服准则)，隧道衬砌采用线弹性本构模型；为降低边界效应影响，左右边界距离隧道中心5倍洞径，下边界距离隧道底部约1.5倍地震波波长[17]，有限元分析模型如图2所示，其长度为120 m，高度为66 m，其中土层1～3厚度分别为22、4、40 m，总单元数量为18 538，单元类型皆为平面应变三角形单元(即CPE3型)。

表1 主要材料物理参数Table 1 Main material physical parameters

图2 计算模型Fig.2 Computational model

土与结构的作用形式为接触面的法向采用硬接触，切向采用摩擦接触，摩擦系数取0.4[18]，通过有限元中的“Contact”功能实现衬砌与土体之间的相互作用，滑动方式选取“Finite sliding”。

模型的边界采用黏弹性边界，其不但可以吸收边界上散射波能量，而且能模拟半无限地基的恢复能力，同时不存在高频失稳和低频整体性漂移的问题[19-20]，能够较好实现半无限区域到有限区域的转换。黏弹性边界实际上就是在模型边界节点上添加对应的弹簧-阻尼元件，弹簧及阻尼的参数计算方法为

(1)

(2)

(3)

(4)

式中：KBN、KBT分别为法相与切向弹簧刚度；CBN、CBT分别为法向与切向阻尼器的阻尼系数；R为波源至人工边界点的距离，现取人工边界到波源的最短距离；cP、cS分别为介质P波与S波的波速；ρ、E、G分别为介质密度、弹性模量、剪切模量；αN与αT分别为法相与切向黏弹性人工边界修正系数，对于二维问题，现分别取0.5和1。

1.3 地震波选取及施加方法

选取三种代表性地震波：El-Centro波、西安人工波、Taft波，峰值加速度为0.2g(g为重力加速度)，加速度时程曲线如图3所示。地震波的施加过程共分为3步：①静力条件下模型地应力平衡，计算边界初始节点反力；②解除固定边界，在对应边界节点施加步骤①计算所得反力，添加黏弹性边界，实现静力平衡状态下的边界转换；③施加地震动。常用的地震动输入方法包括加速度时程输入、位移时程输入、等效节点力时程输入，选用等效节点力时程输入方法。

本文研究中地震波输入方式为SV波，根据马笙杰等[21]的研究，对于二维模型，SV波自模型底部边界垂直输入时，边界等效节点力计算方法如下。

(1)底部边界：

(5)

(2)左侧边界：

(6)

(3)右侧边界：

(7)

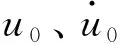
2 模型验证

为证明本文方法的可靠性，建立二维验证模型，如图4所示。模型尺寸为50 m×50 m，在模型顶部及底部中点各布置一个监测点，其中顶部测点为T点(top)，底部测点为B点(bottom)。模型材料各参数分别为：密度ρ=2 000 kg/m3，弹性模量E=300 MPa，泊松比μ=0.25，剪切波速cS=200 m/s，αN与αT分别取0.5和1。单元类型为四节点平面应变单元，单元尺寸为1 m×1 m；在模型底部垂直入射SV波，采用伪狄拉克函数定义输入脉冲波形，入射波的位移时程曲线如图5(a)所示，持续时长0.2 s。

图4 验证模型测点Fig.4 The measuring points of test model

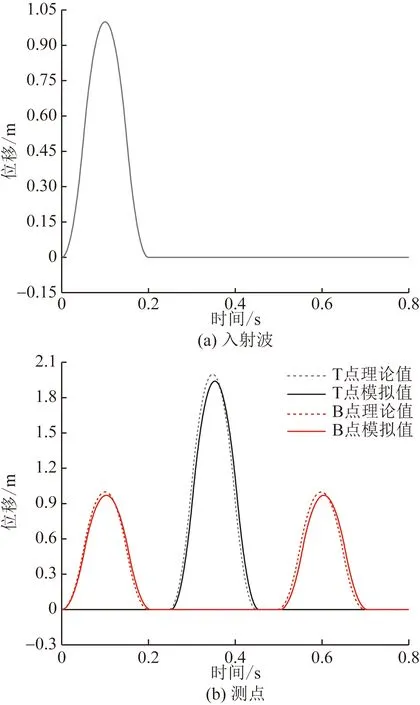
图5 位移时程曲线Fig.5 Displacement time history curves

计算结果如图5(b)所示，分析发现，模型底部施加的入射波在0.25 s以后传递至模型表面，并且顶部测点位移幅值是底部测点的2倍，这与马笙杰等[21]的研究结果一致；同时，分析底部测点位移时程曲线发现，在0.5 s以后入射波从模型顶部反射至底部，波形与初始入射波形一致，且在0.7 s后测点位移恢复为0，之后不再发生变化，说明黏弹性边界有效吸收了反射波，本文研究中所采用方法的正确性得以验证。

3 隧道衬砌结构的地震动力响应规律

根据模型计算结果，选取关键点为研究对象，对加速度、动应力、变形响应特征进行分析，测点位置如图6所示。

图6 测点位置Fig.6 Position of measuring points

3.1 加速度响应特征

通过图7可以发现，El-Centro地震波下各测点加速度时程曲线基本重合，峰值加速度最大值为1.40 m/s2，位于R3测点，最小值为1.36 m/s2，位于L1测点，二者仅差0.02 m/s2。然而，当以L1测点加速度为参照，绘制其余测点相对加速度时程曲线时，如图8(a)所示，发现各测点的加速度又存在一定区别，虽然大部分时间段各测点与L1测点的加速度差在0.1 m/s2以内，但部分时刻相对加速度差值明显，最大达到0.42 m/s2。以差别最显著的R3测点为例，分别绘制另外两种地震波作用下相对于L1测点的相对加速度时程曲线，如图8(b)所示，发现R3的相对加速度也不为0，最大相对加速度分别为0.36、0.21 m/s2。根据上述分析，双连拱隧道在地震中呈现的加速度规律为总体一致但存在一定差异，虽然不会因较大加速度差而产生较为明显“畸变”，但仍可能引起隧道出现不可忽视的变形及应力变化，进而改变隧道安全性。

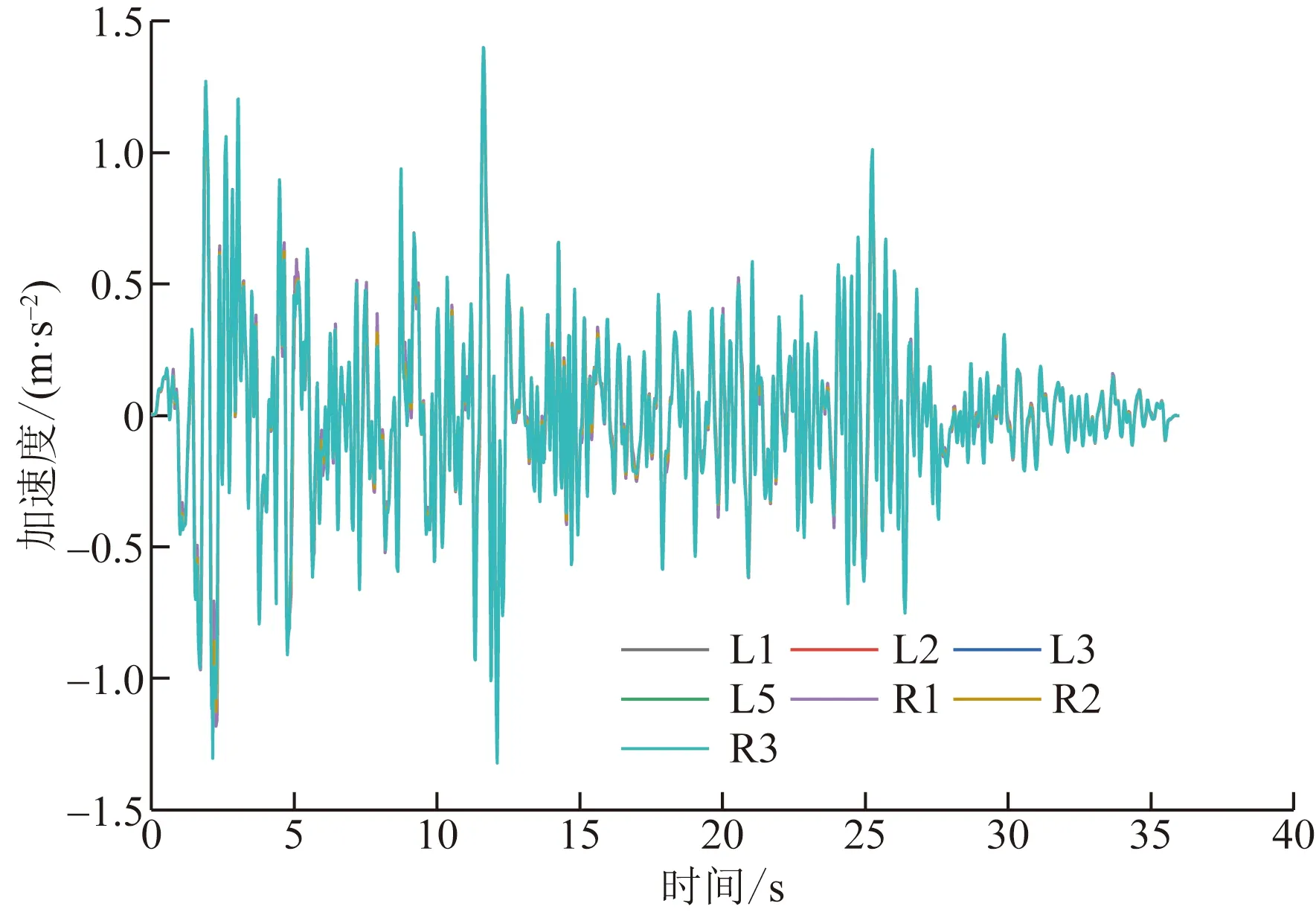
图7 El-Centro波下测点加速度时程曲线Fig.7 Time history curve of measuring point acceleration under El-Centro wave

图8 测点相对加速度时程曲线Fig.8 Time history curve of measuring point relative acceleration

3.2 应力响应特征

根据图9地震波作用下衬砌应力变化时程曲线发现，各测点基本都在11.68 s达到峰值，定义此时刻为最不利时刻，绘制隧道左右洞内边界线应力分布图，如图10所示。分析图9和图10可知，仰拱及拱墙应力变化相对较为缓和，且各点变化趋势基本一致，而中隔墙测点、左右拱脚的应力变化幅度明显高于其余部位。L1点初始Mises应力为0.99 MPa，在11.68 s时达到峰值1.66 MPa，应力增幅约67%，此时地震波加速度正好达到最后一个峰值。之后，L1测点应力总体呈现稳定趋势，变化幅度较小，直至地震结束时该点Mises应力稳定在1.62 MPa左右。

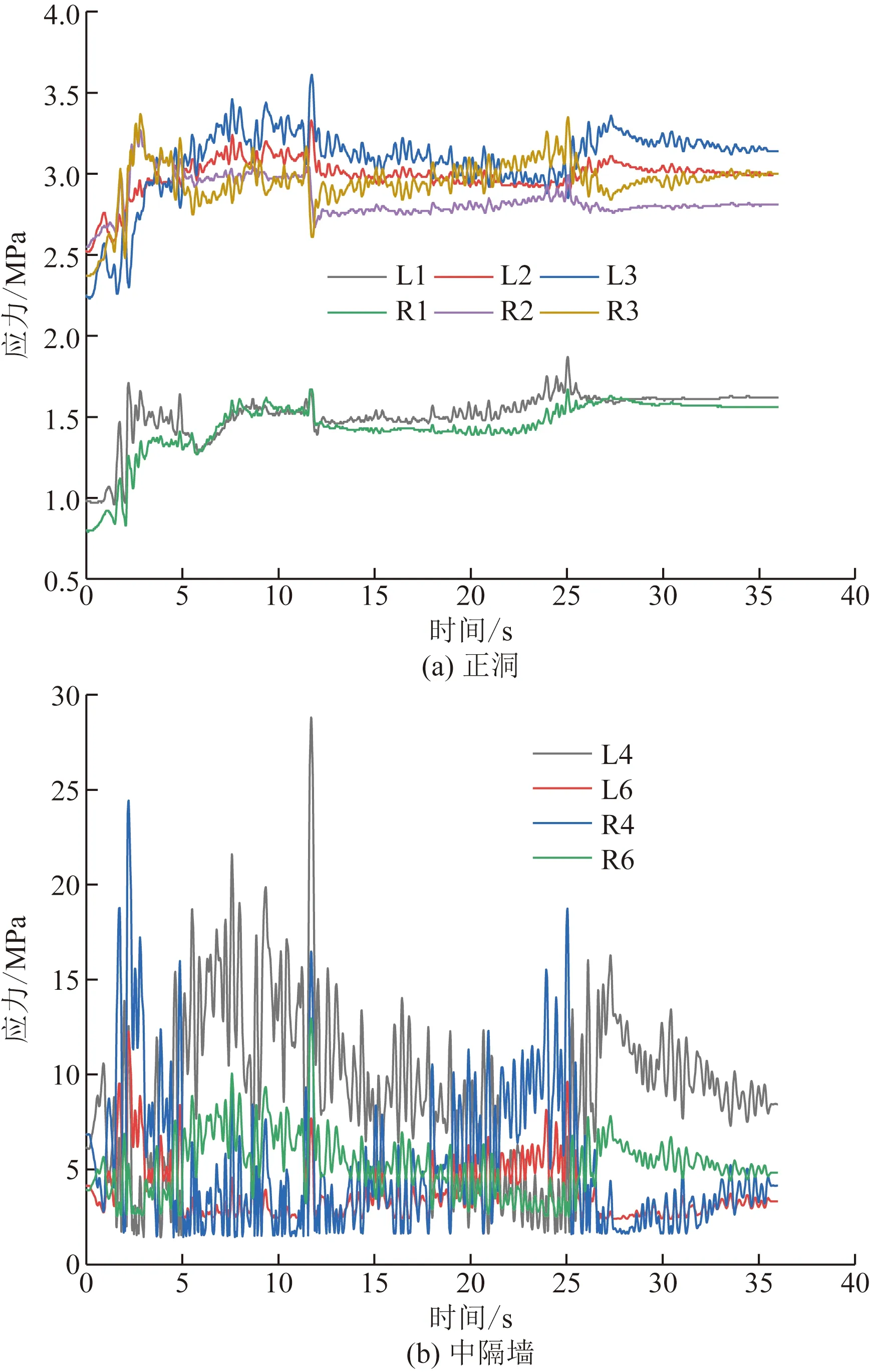
图9 El-Centro波作用下应力变化时程曲线Fig.9 Time history curve of stress variation under the action of El-Centro wave

图10 El-Centro波作用下最不利时刻衬砌应力变化分布Fig.10 Variation distribution of lining stress at the most adverse moment under El-Centro wave

通过图11衬砌应力增量变化时程曲线发现，在地震结束后，测点应力并未归于初始值，结合图12地震前后围岩应力分布的对比可知，地震过程中围岩应力场发生了较为明显改变，即隧道所处应力状态发生了改变。因此在实际工程中，不同于地上结构，地下结构即使在震后未出现明显裂缝、变形等灾害，其围岩应力状态可能也已经发生较大改变，应予以关注。

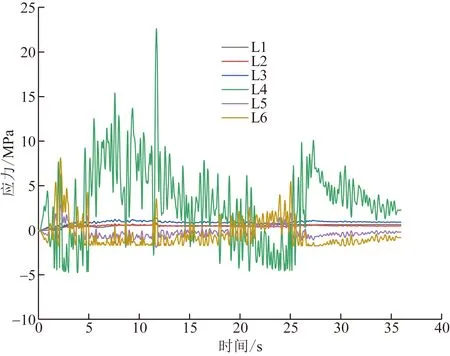
图11 El-Centro波作用下衬砌应力增量时程曲线Fig.11 Time history curve of lining stress increment under El-Centro wave

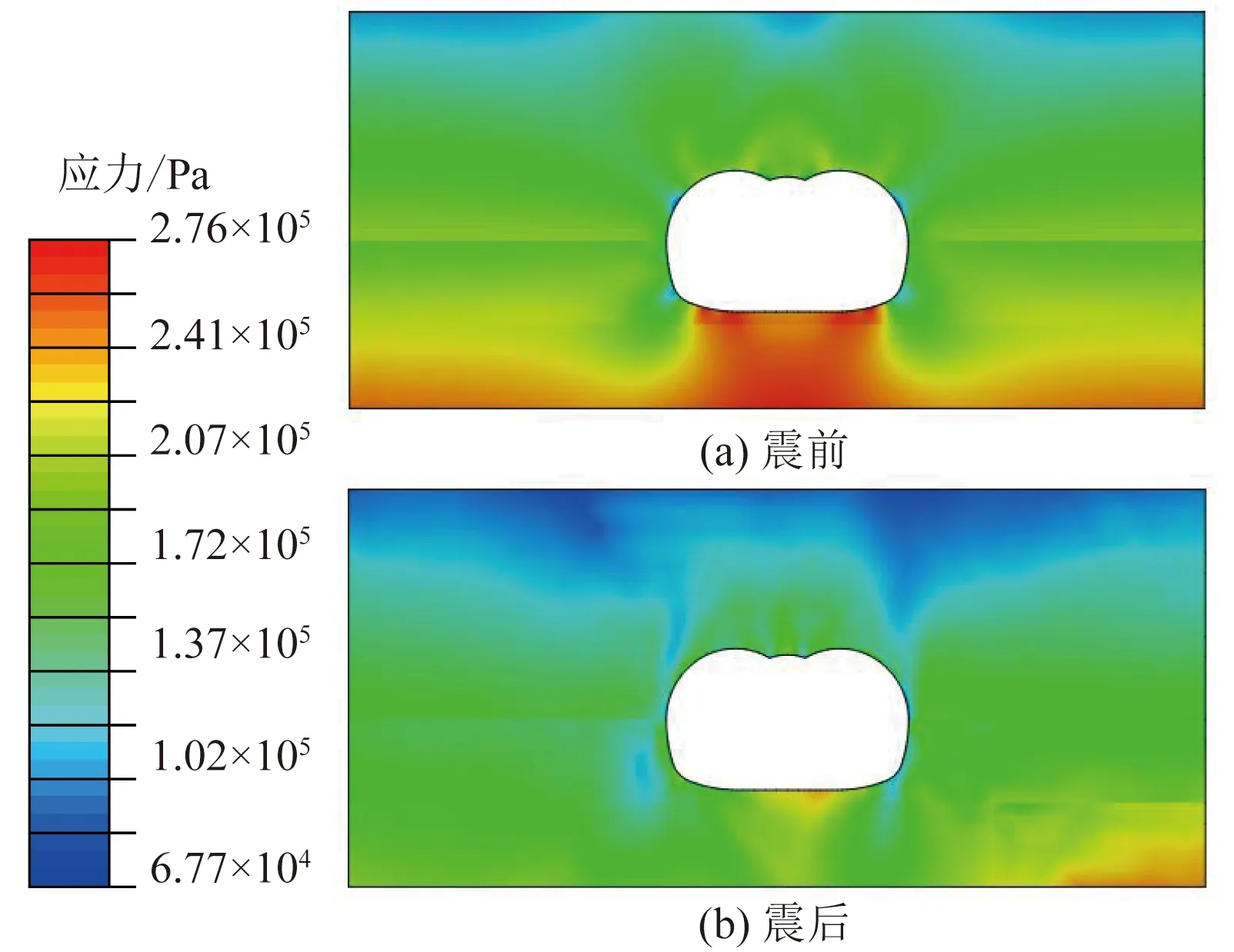
图12 El-Centro波作用下围岩应力分布Fig.12 Stress distribution of surrounding rock under El-Centro wave

对比分析图9和图11，中隔墙墙顶及墙底测点应力变化十分剧烈，L4、R4测点(墙底)最大应力变化量分别达到了17.56、22.62 MPa，L6、R6测点(墙顶)最大应力变化量分别为8.11、9.02 MPa，而L5、R5测点(墙中)最大应力变化量仅3 MPa左右，墙顶及墙底的大幅应力变化对隧道结构的安全性无疑造成了巨大威胁。探究其原因，主要是由于在墙顶及墙底结构有明显拐角(墙顶相对缓和)，存在应力集中现象。在地震作用下，其应力变化幅度显著高于其他部位，是隧道安全的“高风险点”。同时，从西安人工波及Taft波作用下最不利时刻衬砌应力变化分布图(图13)可以发现，中隔墙角点及两侧拱脚应力变化明显比其他测点剧烈，也是本工况中的“高风险点”，即无论何种地震波，隧道结构中存在明显拐角的位置都是潜在风险点，不利于结构的安全性。

图13 最不利时刻衬砌应力变化分布Fig.13 Variation distribution of lining stress at the most adverse moment

在地震作用下，一旦中隔墙应力集中点出现拉压破坏，极有可能引发中隔墙整体性破坏，进而导致隧道坍塌。因此，在隧道设计过程中，尽可能避免“硬转角”的出现，进而避免出现过大应力集中现象，保证隧道在地震中的稳定性、安全性。

为研究中隔墙应力变化剧烈点应力变化内因，以L4点为代表，绘制该测点应力分量变化时程曲线，如图14所示，其中σy为负值时表示受压。可以发现，σx及τxy变化较小，其最大变化量分别为5.32、6.20 MPa，且在5 s以后基本保持稳定；而σy分量最大变化量为22.37 MPa，远大于另外两个分量，因此地震作用对中隔墙风险点的影响主要为竖向应力分量。

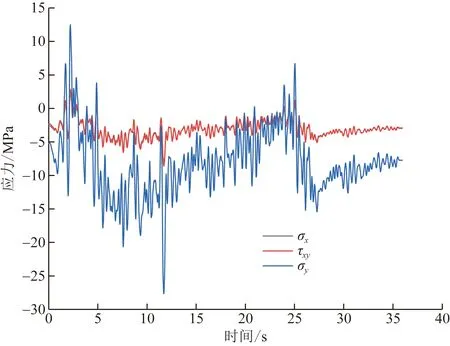
图14 El-Centro波作用L4测点应力分量变化时程曲线Fig.14 Time history curve of stress component variation at measuring point L4 under El-Centro wave action

同时，σy在整个地震过程中波动幅度较大，甚至部分时间段变为正值(即此处混凝土受拉)，最大为12.47 MPa，明显超过了C30混凝土抗拉强度2.01 MPa，使得结构处于危险状态。对比分析墙底两侧测点的σy变化可以发现，L4与R4时程曲线基本呈对称分布，可以认为中隔墙在地震作用下的受力形式与受偏压作用的混凝土柱相似，在抗震设计阶段，应充分考虑中隔墙可能出现的最大拉应力。

3.3 变形响应特征

选取隧道相对变形来研究变形响应特征，图16为El-Centro地震波作用下隧道拱顶-仰拱线(L13、R13)及拱腰线(L25、R25)的水平及竖向(U1、U2)相对位移时程曲线，以U1_L13为例，代表L1与L3测点在水平方向上的相对位移。分析发现，左右洞拱腰线水平方向相对位移基本为0，竖向相对位移趋势基本相同，数值互为相反数，相对位移最大值为8.79 mm；左右洞拱顶-仰拱线的水平相对位时程曲线基本重合，最大值为9.86 mm，而其竖向相对位移几乎为0。综合各点变形规律可以发现，隧道变形规律为上部结构相对于隧道底板随地震作用产生水平偏移运动(假定底板为零位移面)。

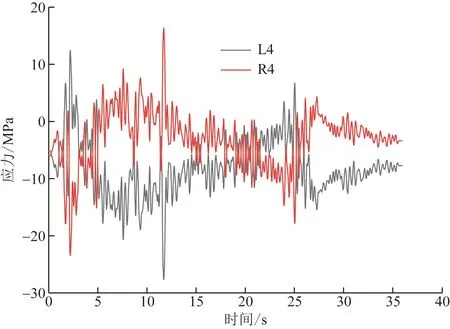
图15 El-Centro波作用下中隔墙对称测点σy应力变化时程曲线Fig.15 Time history curve of σy variation at symmetrical measuring point on the middle partition wall under El-Centro wave

图16 El-Centro地震作用下相对位移时程曲线Fig.16 Time history curve of relative displacement under El-Centro earthquake

为探究不同地震作用下隧道变形规律的差异，以L13的水平相对位移为对象，绘制不同地震作用下相对位移时程曲线，如图17所示。从图17可以看出，El-Centro波作用下隧道的水平相对位移最大，其值为9.86 mm，人工波次之，最大相对位移为7.35 mm，Taft波最小，其最大值为2.12 mm。虽然人工波的最大加速度略大于El-Centro波，然而El-Centro波作用下的隧道变形幅值大于人工波；Taft波作用下隧道相对变形最小，这可能主要是因为本文选取Taft波的加速度幅值小于另外两种波。综上可知，地下结构的变形相应特征除受地震波的最大加速度影响之外，同时还受到地震加速度时程曲线分布形式的影响。