测绘领域中常用坐标系统及其转换计算
2021-11-22王忠礼刘德利
王忠礼,刘德利
吉林建筑大学 测绘与勘查工程学院,长春 130118
0 引言
目前,测绘地理信息类专业在诸多领域获得蓬勃发展,而为空间点的位置描述提供精准空间参考的地球坐标系在其中发挥着重要的作用.在实际应用中,理解并厘清地球坐标系统的种类及同一种坐标系统的不同形式,以及坐标系统的椭球基础及坐标系统的转换等问题,对于实际工程项目中坐标系的合理选用极为重要,这些问题一直困扰着测绘及地信行业工作者[1].另外,以美国的GPS(全球定位系统)、中国的BeiDou(北斗卫星导航系统)、俄罗斯的GLONASS(全球导航卫星系统)以及欧盟的Galileo(伽利略系统)为引领的全球四大著名GNSS系统(全球导航卫星系统),已经获得了长足的发展和应用[2].GNSS系统本质上是通过卫星信号接收机确定到若干已知空间位置的卫星瞬时距离进而计算出空间点位置.为了方便、准确地描述卫星在空间中的位置,需要采用天球坐标系;而描述地面点的位置则需要采用高精度的地球坐标系.为此,厘清地球坐标系的椭球基础、地球坐标系不同形式以及不同地球坐标系之间转换关系,对于从事测绘地理信息类行业工程项目的从业人员选择恰当、合适的坐标系具有重要的作用.
1 我国国家常用的椭球
建立描述地面点位置的地球坐标系需要以地球椭球为基础.目前,世界各国总共定义了至少有70多种不同的几何参数的地球椭球[3].我国常用的地球椭球包括克拉索夫斯基椭球(Krasovsky),IAG75国际椭球(国际大地测量协会1975年国际会议上定义,也称为IUGG75椭球[4])及WGS84椭球.其中,克氏椭球和IAG75椭球为参考椭球,即椭球中心不在地球质心上,椭球旋转轴与地球旋转轴平行;WGS84椭球为总地球椭球,椭球中心处于地球质心上,椭球旋转轴与地球旋转轴重合.椭球参数见表1[2,4].

表1 我国常用的椭球及其几何参数Table 1 Ellipsoid and its geometric parameters in common use
2 同一椭球基础上不同形式的坐标系
为应对不同应用领域的需要,在椭球基础上可以构建3种本质相同形式不同的坐标系:地心(参心)空间直角坐标系、大地坐标系(也称为地理坐标系)及投影平面直角坐标系(测绘领域中常用高斯投影平面直角坐标系).之所以说这3种形式的坐标系本质相同是因为在同一个椭球基础上,3种不同形式的坐标系可以按照数学模型进行严密的公式转换.坐标系定义见表2.

表2 基于椭球的3种不同形式的坐标系Table 2 Three different forms of coordinate system based on ellipsoid
3 地球空间信息领域中常用的地球坐标系统
基于不同的椭球、不同的定位和定向参数,可以构建不同的坐标系统.我国自建国以来,分别建立了1954年北京坐标系、1980年国家坐标系(也称为西安坐标系),及CGCS 2000坐标系.加上美国建立的WGS 84坐标系,目前我国在地球空间信息领域常用的4种坐标系统见表3.

表3 中国常用地球坐标系统Table 3 The earth coordinate systems commonly used in China
4 坐标系统之间的转换
4.1 同一个椭球基础上不同形式的坐标系转换
在同一个椭球基础上的3种不同形式的坐标系之间的转换模型是严密的.地心(参心)空间直角坐标系与大地坐标系之间的转换关系公式:
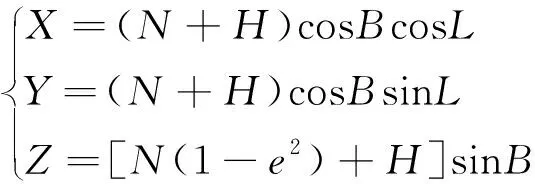
(1)
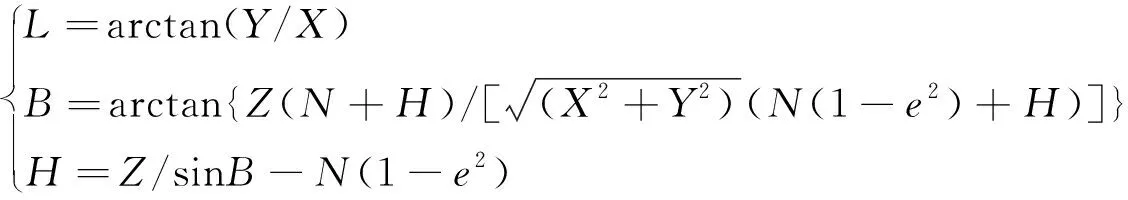
(2)
式中,(X,Y,Z)为地心(参心)空间直角坐标系坐标;(B.L,H)为大地坐标系坐标,其中H为大地高;N为卯酉圈曲率半径;e为椭球的第一偏心率.
大地坐标系坐标与高斯平面直角坐标系坐标之间的转换称为高斯投影换算.空间点的大地坐标转换为高斯平面直角坐标称为高斯投影正算,空间点的高斯平面直角坐标转换为大地坐标称为高斯投影反算.高斯投影正反算的具体内容可以参阅大地测量学基础教材[5].
4.2 不同椭球基础上坐标系的转换[6]
不同椭球基础上的坐标系之间转换模型是不严密的,一般采用布尔莎模型进行转换.具体又分为利用已知重合点的三维空间直角坐标进行“七参数法”坐标转换和利用已知重合点的二维高斯平面直角坐标进行“四参数法”坐标转换.
“七参数法”转换步骤:将不少于3个已知点的两套不同椭球基础上坐标系坐标转换为各种椭球基础上的地心(参心)空间直角坐标系坐标;代入公式(3)布尔莎模型计算出七参数;将待定点的源椭球基础上的源坐标代入布尔莎模型计算出目标椭球基础上的目标坐标.
“四参数法”转换步骤:将不少于2个已知点的两套不同椭球基础上坐标系坐标转换为各种椭球基础上的高斯平面直角坐标系坐标;代入公式(4)布尔莎模型计算出四参数;将待定点的源椭球基础上的源坐标代入布尔莎模型计算出目标椭球基础上的目标坐标.
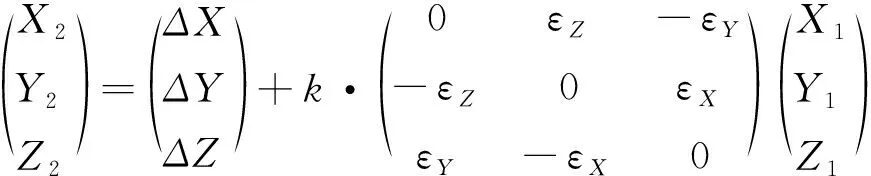
(3)
式中,(X1Y1Z1)T为源坐标系坐标;(X2Y2Z2)T为目标坐标系坐标;(ΔX,ΔY,ΔZ)为两个坐标系原点平移参数,εX,εY,εZ为三个坐标轴的旋转参数,k为两个坐标系之间的尺度比例,为尺度参数.
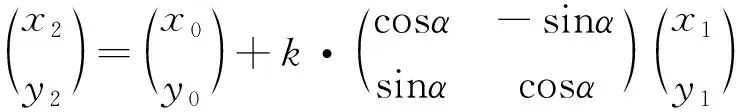
(4)
式中,(x2,y2)为目标坐标系坐标;(x1,y1)T为源坐标系坐标;(x0,y0)T为两个坐标系坐标原点平移参数;α为两个坐标系的X轴的旋转角,为旋转参数;k为两个坐标系之间的尺度比例,为尺度参数.
5 坐标系统转换计算实例
坐标系统的转换可以采用计算机编程语言进行程序设计与代码实现,也可以采用Matlab作为计算平台进行方便的计算转换.也可以藉助商业软件进行便捷的转换实现.
图1以广州中海达测绘仪器有限公司研发的HDS2003软件中的坐标转换工具COORD Global Manage2.0为例[3],进行坐标系统转换计算.

图1 HDS 2003软件坐标转换计算工具界面Fig.1 HDS 2003 software coordinate transformation calculation tool interface
5.1 同一椭球基础上的不同形式的坐标系转换计算
首先在软件界面中选择源椭球和目标椭球,然后选择源坐标系和目标坐标系,最后输入源坐标系坐标,在设置菜单中设置相应的投影带,点击“转换坐标”按钮即可实现转换.
表4分别为WGS 84椭球上的大地坐标系坐标转换为其他两种形式的坐标系坐标,IAG 75椭球上地心(参心)空间直角坐标系坐标转换为其他两种形式的坐标系坐标计算结果.

表4 同一椭球上不同形式的坐标系转换计算Table 4 Conversion calculation of different forms of coordinate systems on the same ellipsoid
5.2 不同椭球上的坐标系统转换
选择坐标转换工具COORD GM的“设置”菜单“计算七参数”、“计算四参数”菜单项,输入若干点(“七参数”至少3个已知点,“四参数”至少2个已知点)的源坐标系统椭球及坐标和目标坐标系统椭球和坐标,选择“布尔莎”计算模型即可计算出不同椭球基础上的坐标系统之间的转换参数.表5为采用3个已知点的两套坐标系坐标计算的“七参数”及“四参数”结果.

表5 不同椭球基础上坐标系之间转换计算Table 5 Conversion calculation between coordinate systems on the different ellipsoid
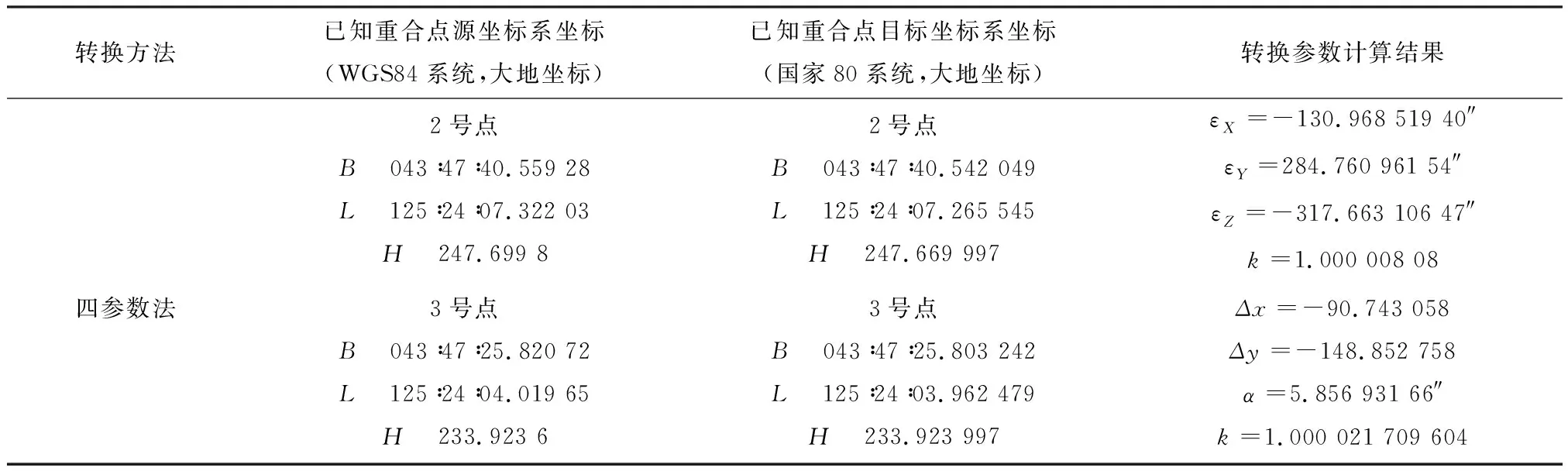
续表5
6 结语
本文针对测绘领域中常用的地球坐标系的椭球参数、分类及坐标转换进行了较为详细的梳理,基于吉林建筑大学GNSS实训场地建设的成果,采用中海达测绘仪器有限公司研发的坐标转换工具进行了实例计算,对于测绘地理信息类专业人员理解并正确使用地球坐标系有一定的参考价值.
