西南地区用户侧综合能源系统优化配置

陈涛，吴高翔，周念成，吕小红，刘维，吴雪翚

（1.国网重庆市电力公司电力科学研究院，重庆 401120；2.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044；3.国网重庆市电力公司，重庆 400015）

0 引言

我国西南地区地形架构远距离能源输送管道难度较大，且该地区为典型夏热冬冷地区，热、冷负荷较大。但西南地区拥有丰富的可再生能源资源[1]，适合建设以水能、天然气、风能与光能互补的综合能源系统。通过对西南地区综合能源系统进行优化配置，可以实现可再生能源的大规模消纳，提高能源的利用率[2]～[4]。

目前，关于用户侧综合能源系统优化配置已有相关研究。文献[5]提出了含有冷热电联供和风电的综合能源系统优化调度模型，并将天然气系统安全约束集成到优化调度策略中。文献[6]考虑了电力系统与天然气、供热系统的联合优化运行，建立了基于机会约束规划的热电能量综合优化模型。文献[7]根据新能源接入的波动不确定性和峰谷参数的不同，建立了一种电能、热能、氢能集成的储能系统及其协调优化配置模型。文献[8]针对热电联供经济调度问题，提出了多目标优化与综合决策相结合的两阶段调度方法。文献[9]以优化配置能量枢纽的设备类型和容量为目标，考虑综合需求侧响应及能量枢纽运行约束，构建了可显著降低年运行费用的优化配置模型。文献[10]考虑热、冷、电3种能源系统的耦合关系，以充分利用可再生能源、提高综合系统能源利用效率为目标，提出一种综合能源系统优化调度方法。上述研究以理想工况用能场景为基础，进行用户侧综合能源系统优化配置，但实际中由于环境及设备出力影响，理想工况下的优化配置模型不够精确，对系统规划的准确性和合理性有较大影响。

本文针对用户侧综合能源系统，结合西南地区特定地域的能源现状，首先针对转换效率系数变化的全工况用能场景，建立了各设备的全工况数学模型。其次以综合能源系统年投资、运行成本为目标，通过分段线性化处理和最小二乘法拟合，提出了一种面向西南地区用户侧的综合能源系统优化配置模型。最后通过算例验证所提模型的有效性。

1 西南地区综合能源系统典型结构

西南地区拥有丰富的水、天然气和风、光资源。结合西南地区山地运输条件及地质条件，临近用户设置具备发电、供热、供冷功能的设备，在能源互补互济和梯级利用基础上，建立综合能源系统，其结构如图1所示。

图1 西南地区综合能源系统结构Fig.1 Structure of integrated energy system in Southwest China

该系统利用以天然气为燃料的燃气锅炉、燃气内燃机、燃气轮机等设备产生电力，其排放的高温烟气中所含的余热被回收利用，冬季用于供暖，夏季用于驱动吸收式制冷机等设备供冷，外部热网还直接为负荷供热。系统中接入了风力、光伏、水能等可再生能源供电，其出力特性不可控，外部电网可直接为负荷供电。除了上述主要设备之外，为了增加系统供能的稳定性和可靠性，一般还要配备蓄能装置等辅助设备。综合能源系统因包含天然气、热能、风能、太阳能、水能、电能等多种能源输入和冷、热、电能多种输出，并有能源转换装置和蓄能装置提供系统内能源的融合协同，一方面实现了能源梯级利用，另一方面实现不同能源系统之间的耦合，提高能源利用效率。

2 优化配置数学模型

2.1 目标函数

总成本：

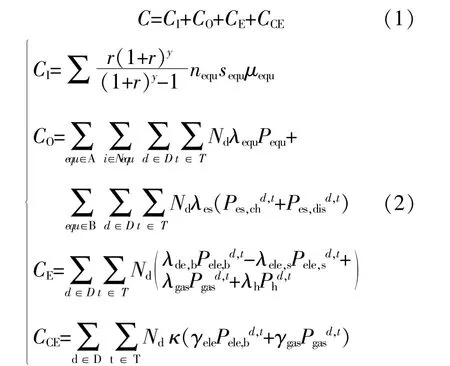
式中：C为年度总成本；CI为年投资成本；CO为年运行成本；CE为年运行能耗成本；CCE为年环境成本；nequ为设备的台数；sequ为单台设备的容量；μequ为设备的单位容量投资成本；r为年利率；y为设备的寿命；d为典型日类别，d=1表示冬季，d=2表示夏季，d=3表示过渡季；Nd为典型日累计天数；Pequ为设备的功率；λequ为设备单位功率的运行成本；Pes，chd，t和Pes，disd，t分别为储能ES的充能和放能功率；λes为储能单位充放能功率的成本；Pele,bd，t为从外部电网的购电功率；Pele，sd，t为向外部电网的售电功率；λde，b和λde，s分别为购、售电单价；Pgasd，t为从外部气网的购气功率；λgas为购气单价；Phd，t为外部热网的购热功率；λh为购热单价；κ为碳排放成本；γele，γgas分别为单位电功率和天然气功率的等值CO2排放因子；A为{GT，GE，PV，WT，GB，WB，AC，HP}；B为{EES，TES，CES}。

2.2 功率平衡约束

天然气的燃料功率平衡约束、水资源为主的热、冷功率平衡约束、风光资源为主的电功率平衡约束分别为

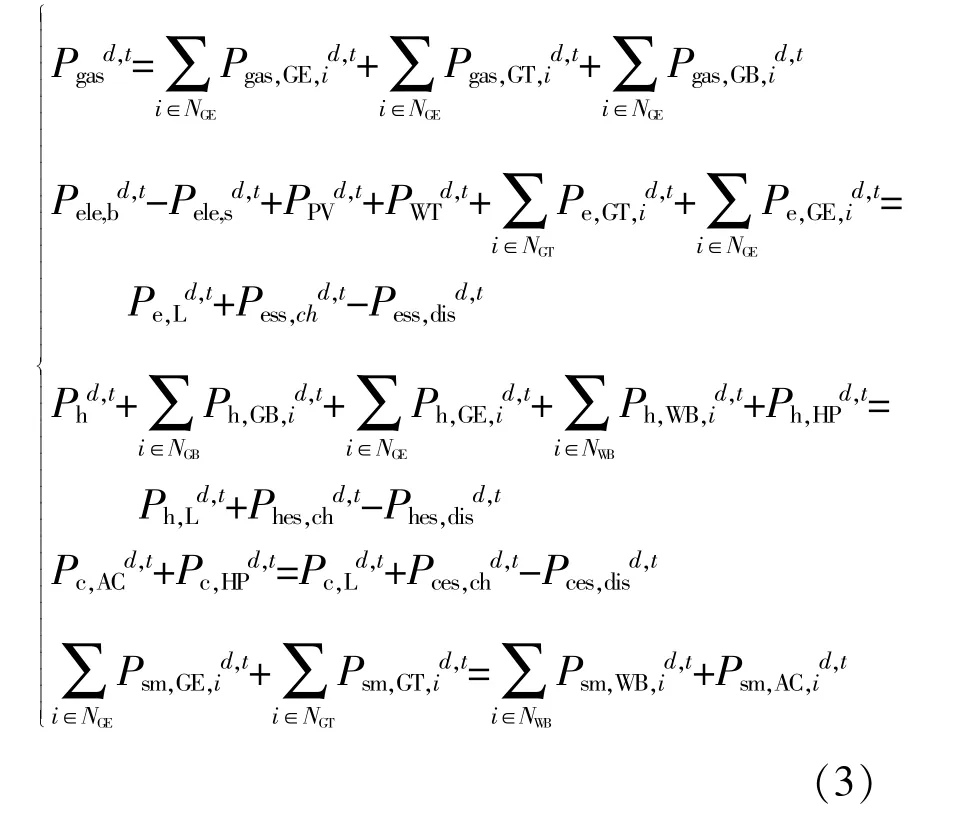
式中：Pgas，GE，id，t，Pgas，GT，id，t，Pgas，GB，id，t分别为天然气内燃机、燃气轮机和燃气锅炉在t时刻消耗的天然气；PPVd，t，PWTd，t，Pe，GT，id，t，Pe，GE，id，t分别为光伏、风电、燃气轮机和天然气内燃机的输出电功率；Pe，Ld，t为电负荷；Pess，chd，t，Pess，disd，t分别为电储能的充放电功率。热功率平衡约束中，Ph，GB，id，t，Ph，GE，id，t，Ph，WB，id，t，Ph，HPd，t分别为燃气锅炉、天然气内燃机、余热锅炉和水源热泵的输出热功率；Ph，Ld，t为热负荷；Phes，chd，t，Phes，disd，t为热储能的充放能功率；Pc，ACd，t，Pc，HPd，t分别为吸收式制冷机和水源热泵的输出冷功率；Pc，Ld，t为冷负荷；Pces，chd，t，Pces，disd，t为冷储能的充放能功率；Psm，GE，id，t，Psm，GT，id，t分别为天然气内燃机和燃气轮机输出高温烟气功率；Psm，WB，id，t，Psm，AC，id，t分别为余热锅炉和吸收式制冷机消耗的高温烟气功率。

2.3 能源设备运行约束

（1）天然气内燃机的数学模型

式中：ηe，GE，id，t为天然气内燃机i在季节d时刻t的发电效率，随天然气内燃机出力变化而变化；fh，GE，id，t为天然气内燃机i缸套水余热占总余热的比重；fsm，GE，id，t为天然气内燃机i烟气余热占总余热的比重；τGE，id，t为天然气内燃气i的启停状态，为0，1二进制变量；αGEmin，αGEmax分别天然气内燃机的最小和最大电功率系数；当天然气内燃机数量i大于实际数量nGE时，τGE，id，t=0为停止状态，当天然气内燃机数量i小于实际数量nGE时，τGE，id，t=1为停开启状态。

（2）燃气轮机

燃气轮机的数学模型为

式中：ηe，GT，id，t，ηh，GT，id，t分别为燃气轮机i在季节d时刻t的发电和发热效率，随燃气轮机出力变化而变化；τGT，id，t为燃气轮机i的启停状态，为0，1二进制变量；αGTmin，αGTmax分别燃气轮机的最小和最大电功率系数。

（3）燃气锅炉

由于燃气锅炉运行效率较高且非常稳定，一般认为其在部分负荷下的工作效率不变，即输出热量与输入能量保持线性关系，其供能数学模型可以表示为

式中：ηGB为燃气锅炉的发热效率，为恒定值；τGB，id，t为燃气锅炉i的启停状态，是0，1二进制变量；αGBmin，αGBmax分别为燃气锅炉的最小和最大热功率系数。

（4）余热锅炉

余热锅炉的数学模型为

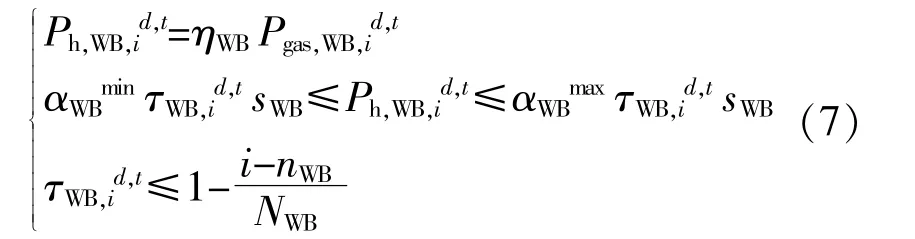
式中：ηWB为余热锅炉的热效率，为恒定值；τWB，id，t为余热锅炉的启停状态，为0，1二进制变量；αWBmax为余热锅炉的最大热功率系数。

（5）吸收式制冷机

吸收式制冷机的数学模型为

式中：COPACd，t为吸收式制冷机的能效系数，其值随着制冷量的增长而增长，近似线性关系；αACmax为吸收式制冷机最大制冷功率系数。

（6）光伏和风力发电系统

当光伏和风力发电系统出力过剩，导致系统难以消纳时，可允许其降出力运行，则光伏和风力发电系统的实际出力满足约束条件为

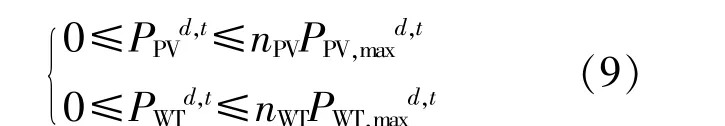
式中：PPVd，t为光伏的实际功率，小于预估功率；PWTd，t为风力的实际功率，小于预估功率。

（7）水源热泵

水源热泵利用水资源中蕴含的太阳能资源作为冷热源，采用热泵原理，通过水能作为综合能源系统的输入，实现系统中冷能、热能的负荷需求。

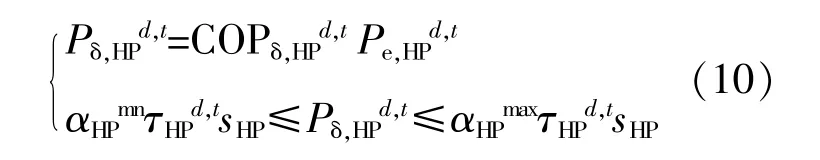
式中：COPδ，HPd，t为水源热泵的能效系数，其物理意义为水源热泵制热运行时的制热量与有效输入功率之比。水源热泵在不同运行工况下，其能效系数会发生变化，即COPδ，HPd，t不是一个常数，而是一个与冷热源侧水温和部分负荷率相关的函数；τHPd，t为水源热泵的启停状态，为0，1二进制变量；αHPmn，αHPmax分别为水源热泵的最小和最大输出功率系数。

（8）蓄能装置

蓄能装置的特性可描述成设备自身容量、最大蓄能状态、蓄能输出功率和蓄能效率等几部分，建立的蓄能装置充放能数学模型为

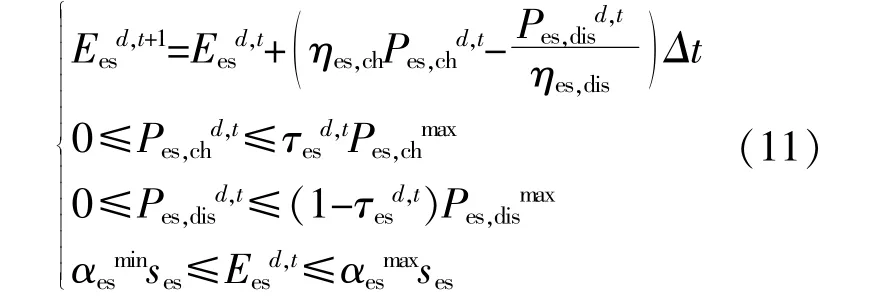
式中：τesd，t为蓄能装置充放能状态；ηes，ch，ηes，dis为储能装置充放能效率系数，效率可达90%；Eesd，t为蓄能装置储存的能量；αesmin，αesmax分别为蓄能装置最小和最大储存的能量系数，分别取0.2和0.9。

2.4 运行设备最小启停时间约束

运行设备最小启停时间约束包括机组最小停机时间和机组最小连续运行时间，其表达式为

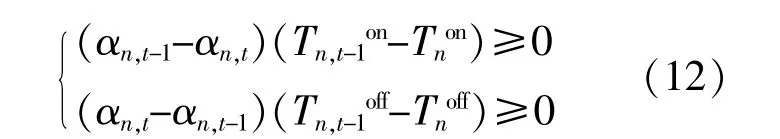
式中：Tn，ton，Tn，toff分别为第n台运行设备在第t个调度时段时已经连续运行和停机的时间；Tnon，Tnoff分别为第n台运行设备的最小连续运行和停机时间，设备包括配置的燃气锅炉、燃气内燃机、燃气轮机和余热锅炉。

2.5 能源设备模型线性化处理

本文建立的综合能源系统优化调度模型是一个复杂的混合整数非线性规划问题，须要先将该问题转化为混合整数线性规划问题，才能进行求解。以燃气内燃机为例，天然气功率可表示为电功率和负荷率的非线性函数。根据已知的发电功率与负荷率函数关系，将该非线性曲线按照0.1 p.u.的等效间隔，分段进行线性化处理。每个间隔内的曲线函数为

式中：Lk为线性化系数；Rk为线性化的常数；引入二进制变量τgas，GE，i，kd，t，判断天然气内燃机输出电功率是否在k个区间内，则天然气功率可以表示为

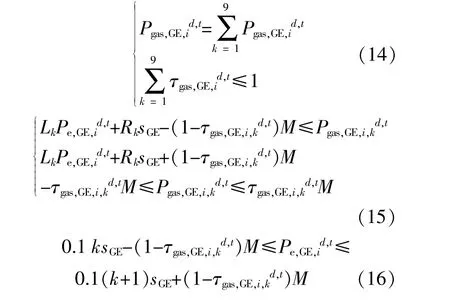
式（14）表示天然气内燃机功率为各区间功率之和，且限制了天然气功率只能位于一个功率区间内；式（15）表示天然气功率在第k个区间内时，满足式（13），否则等于0；而式（16）则限定了输出电功率的所处的区间。

为了进一步分析其他能量转换模型的特点，图2给出了相应功率关系曲线。

图2 输入输出功率关系曲线Fig.2 Relation curve of input and output power

由图2可知，缸套水余热、烟气余热功率与电功率的关系曲线弯曲幅度较大，可以采用上述方法进行分段线性化处理。燃气轮机天然气功率、热功率与电功率，水源热泵电功率与输出冷、热功率关系曲线可以直接近似为一条线性函数，该函数系数可以通过最小二乘法获得。

3 算例分析

3.1 参数设定

以西南某地区综合能源系统为仿真对象，其拓扑如图3所示。

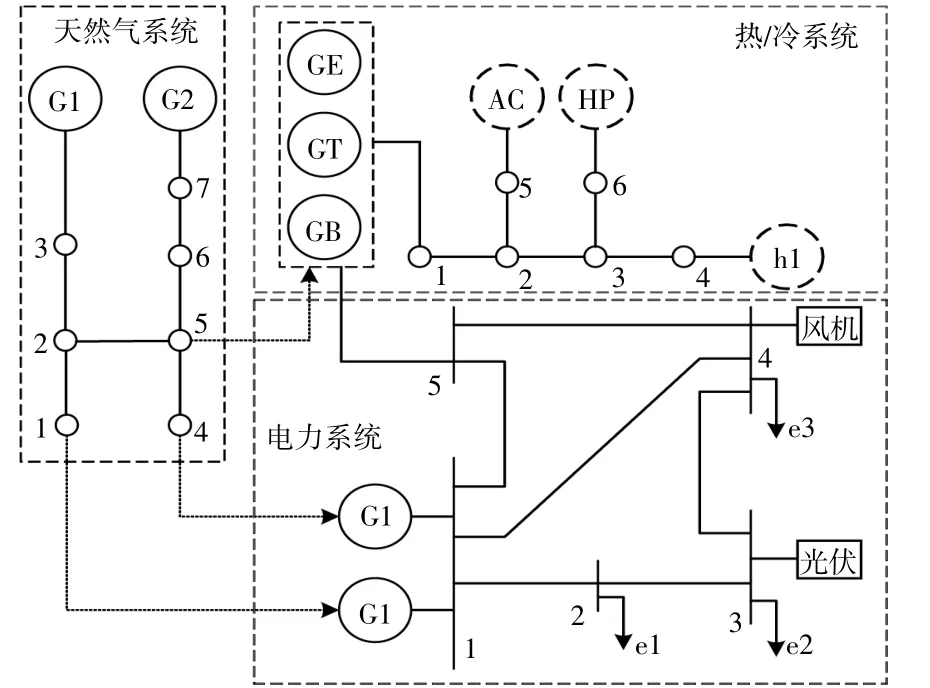
图3 综合能源系统示意图Fig.3 Schematic diagram of integrated energy system

该地区夏季湿热、冬季阴冷，冷热供给需求大，年采暖和供冷需求长达185 d左右；所以该综合能源系统选取时间段365 d分为冬季供热典型日95 d、夏季供冷典型日90 d和过渡季典型日180 d，分别获得冬季、夏季和过渡季典型日的工况场景。其中冬季、夏季、过渡季和新能源功率曲线如图4所示。系统中配置的水源热泵考虑具备制热制冷双重工作模式，在冬季进入制热模式为系统提供热量，在夏季进入制冷模式提供冷能。在冬季，由于系统无制冷需求，吸入式制冷机被关闭[11]。

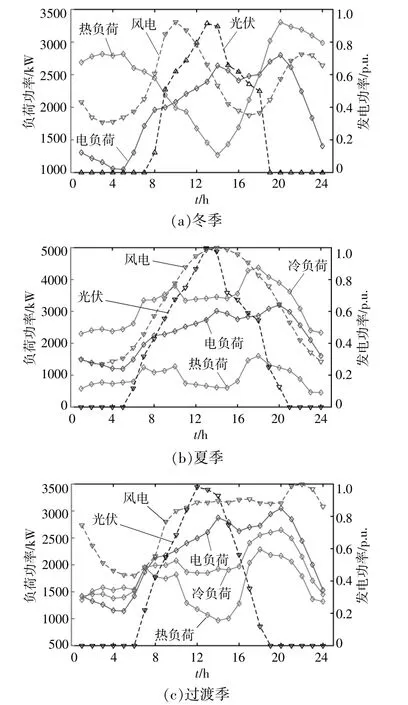
图4 典型日负荷和新能源功率曲线Fig.4 Curve of load and new energy power in typical day

在综合能源系统中，输入能源为风能、太阳能、外购电力、热能和天然气。其中，光照、风力的输入成本为零；外购电力、热力、天然气的等效成本分别为1.2，0.5，0.5元/（kW·h），向外部电网售电价格为0.2元/（kW·h）。本文中的各设备装置参数如表1所示。

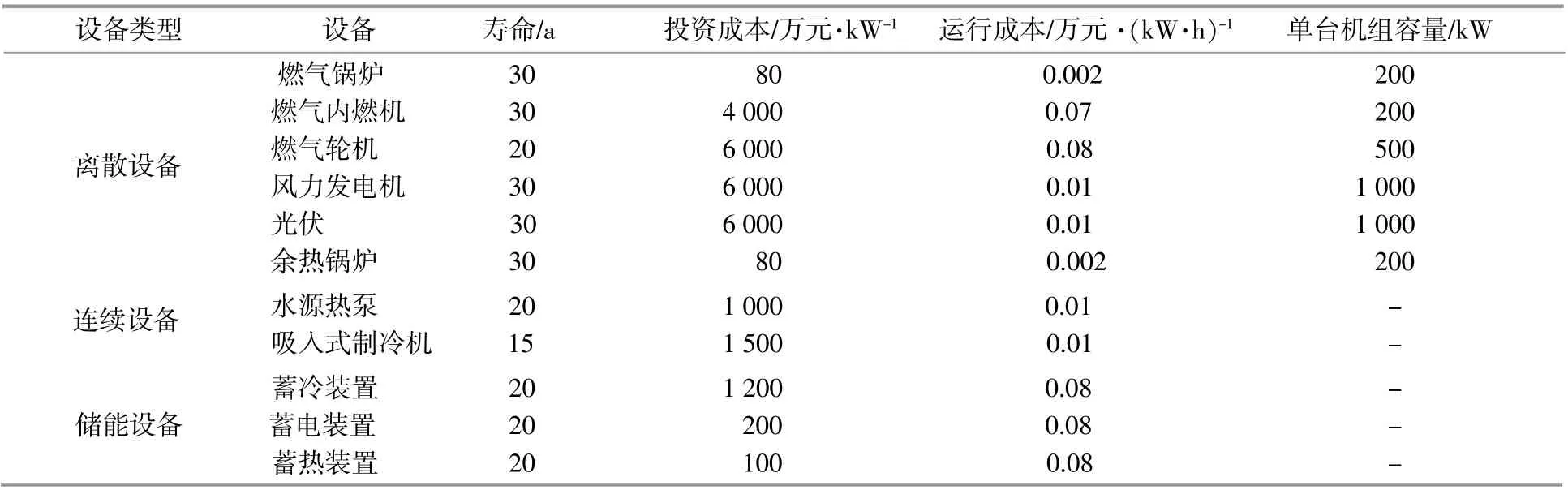
表1 设备装置参数Table 1 Device parameters of equipment

3.2 仿真结果分析

为了比较新能源系统对用户侧综合能源系统优化配置的影响，本文对是否考虑风光出力的综合能源系统优化配置进行对比分析。方案1未考虑风光出力，外部电网和系统内天然气通过燃气内燃机和燃气轮机可以为电负荷供电；外部热网和系统内天然气通过燃气锅炉和燃气内燃机可直接对热负荷供热，也可通过烟气使余热锅炉产生热能；系统内的电能通过燃气内燃机和燃气轮机产生的烟气通过吸收式制冷机产生冷能。系统内的蓄电、蓄热、蓄冷装置在系统内起到削峰填谷的作用。方案1不是最优配置的综合能源系统，没有风光出力导致购电成本、运行成本和环境成本显著增加。方案2考虑风光出力，其中风力发电机、光伏设备分别配置5台、1台，容量分别为5 000 kW和1 000 kW。风能和太阳能产生的电能可直接为电负荷供电，也可通过水源热泵制热制冷，分别供能给热负荷和冷负荷，方案2为最优配置的综合能源系统。

方案1，2配置结果如表2所示。

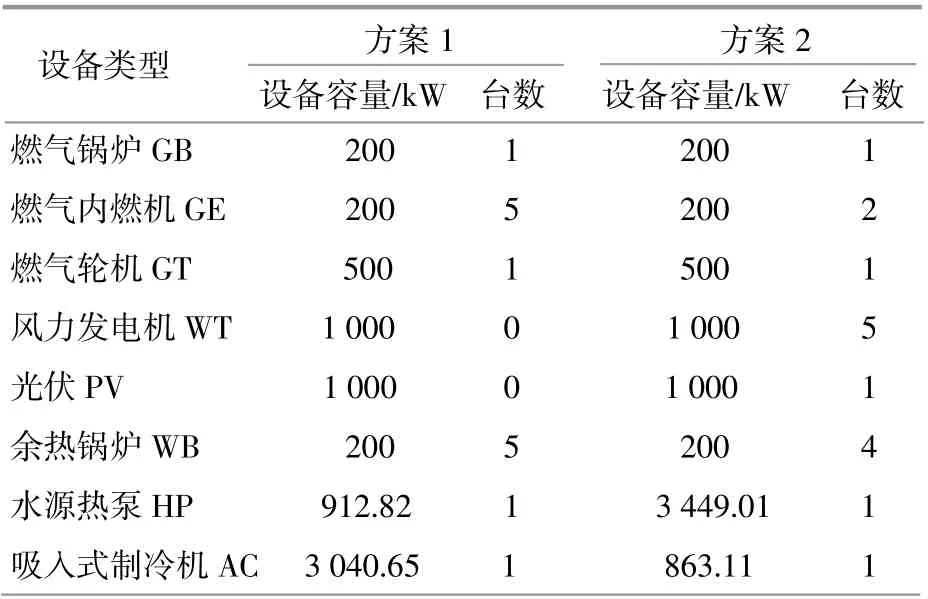
表2 综合能源系统结构配置结果Table 2 Configuration results of integrated energy system

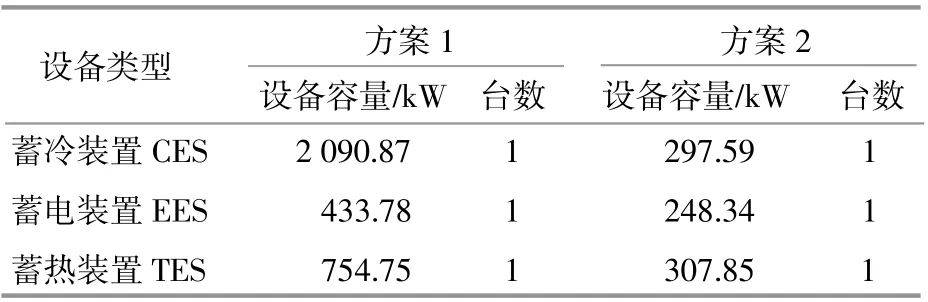
续表2

两种不同方案的成本如表3所示。

表3 两种不同方案的成本Table 3 The cost of 2 cases

由表3可知，方案2的总成本比方案1减少1 903.22万元，约为67.07%。方案2的投资成本高于方案1，原因是风机和光伏设备的投入，然而方案2的运行维护成本、运行能耗成本和环境成本均比方案1减少。由于方案2中增加了5台风机和1台光伏设备，且风机和光伏设备的投资成本较高，所以投资成本较方案1增加211.21%，约为337.33万元。方案2中燃气内燃机的数量显著减少且风机、光伏设备接入，但是由于燃气内燃机维护成本高，风机、光伏设备维护成本低，所以运行维护成本降低了37.58%，约为38.54万元。由于可再生能源发电无需购电成本，方案2中购电成本显著降低，且热泵成本低但需求显著增加，蓄电成本高但需求显著下降，运行能耗成本也减少了85.47%，约为2 179.08万元。方案1中依靠外部电网、热网和系统内天然气供能，而方案2中有风能和太阳能发电，可再生能源的接入较传统的能源利用方式而言，CO2排放量显著降低，环境治理成本也随之降低；方案2中环境成本减少88.97%，约为22.93万元。因此，本文提出的用户侧可再生能源接入的综合能源系统规划模型比传统的综合能源系统有更好的经济效益和环境效益。

3.3 全工况模型与恒定系数模型对比

考虑全工况场景，采用本文建立的优化求解模型对系统配置进行求解；同时使用恒定系数模型对系统进行配置，其中恒定系数模型中设备转换效率为常数，对比结果如表4所示。为了考查设备效率变化对配置结果的影响，恒定系数模型分别采取了各设备在部份负载率（PLR）为0.3和1.0的效率，其余条件均与与全工况模型相同。

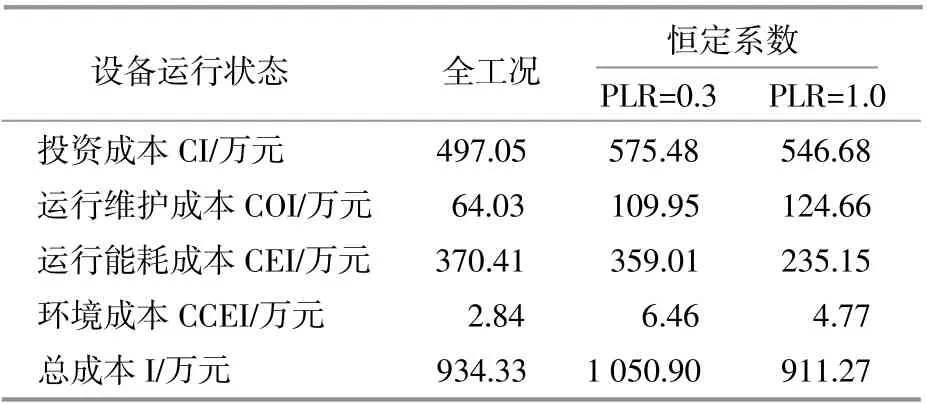
表4 全工况与恒定系数模型成本对比Table 4 Cost comparison between all operating condition and constant coefficient model

西南地区综合能源系统优化配置模型选取了一年中冬季、夏季、过渡季中的典型日工况场景进行模拟，在算例中的求解时间为7 850.54 s，可以满足系统配置需求。采用恒定系数PLR=1.0时，将得到3个方案中成本较低的配置结果，而采用恒定系数PLR=0.3时，负载率低，将得到3个方案中成本较高的配置结果。根据全工况模型和恒定系数模型成本对比，采用全工况模型的年总成本为934.33万元；对于恒定系数模型，在PLR=0.3和1.0的情况下，年总成本分别为1 050.90,9 11.27万元。可见，在采用恒定系数模型对系统进行配置时，由于得出的成本结果较低或较高，用能经济性和负荷多样性得不到满足。采用全工况模型时，由于设备转换效率随着系统出力变化而变化的特性，各种能源设备协调耦合工作，可满足用户用能需求并降低运行成本。

4 结论

基于西南地区特定地域的能源现状，以及系统内各运行设备效率随环境和出力变化而变化的特点，本文建立了一种全工况用能场景下的容量优化配置模型，并得出了西南地区综合能源系统的最优规划配置方法。具体结论如下：①可再生能源接入的优化配置方案可以实现能源的梯级利用和多能互补，缓解高峰时段用电紧张，减少购电成本和碳排放成本，从而提高系统的经济效益和环境效益；②采用恒定系数模型对系统进行优化配置，可能导致无法满足负荷要求或者运行成本较高，而全工况模型转换效率实时变化特性可得到更合理的配置结果。

利用本文所建立的用户侧综合能源系统优化配置方法，通过系统能源输入、转换、储存的互补，可使综合能源系统在外部能源输入、西南地区本地资源供应、环境友好和系统配置合理条件下，最大程度上降低系统年度总成本。