波陡对于扭王字块稳定性影响的试验研究
2021-11-21柳淑学李金宣张昊宸
郭 栋,柳淑学,李金宣,张昊宸
(大连理工大学 海岸和近海工程国家重点实验室,大连 116024)
斜坡式防波堤作为一种抵御海浪入侵的重要水工建筑物,其护面块体的稳定性极大程度上影响斜坡堤的实用性。自1938年Iribarren提出护面块体的稳定性计算公式以来[1],国内外不少学者提出了多种不同的护面块体稳定重量计算公式[2]。国内外港口规范中给出了不同的计算方法,王眯等[3]分析了中外规范中对护面块体稳定性计算标准的差异。在这些公式中,应用较为广泛的是Hudson[4]提出的计算公式。基于该公式,戈龙仔和高峰[5]进行了新型消浪块体(“十字”型块体)在防波堤断面上坡度确定的试验研究,发现块体边坡坡度与块体稳定重量并不是如Hudson公式所体现的反比例关系,而是呈抛物线变化规律。虽然Hudson公式在一般的情况下都能得到较好的结果,但该公式存在的主要不足为只考虑了波高的影响,而未考虑周期的影响。
为了进一步研究波浪的波陡对于护面块体稳定性的影响,本文采用两种不同重量的扭王字块作为斜坡堤的护面块体,针对3种不同坡度的斜坡堤,采用6组不同波陡的波浪进行物理模型试验,研究给出较大范围波陡对护面块体稳定性的影响规律。
1 模型试验布置和条件
1.1 试验布置
试验在大连理工大学海岸和近海工程国家重点实验室的波流水槽中进行,波流水槽长69 m、宽2 m、深1.8 m,水槽一侧装有自行研制的不规则波造波机、微机控制与数据采集系统及2台1 m3/s轴流泵的双向造流系统。水槽两端均设置消能器用于吸收波浪。同时水槽造波机具有主动吸收功能。试验中波浪要素的测定采用本实验室研制的DLY-1型浪高应变组合仪。
1.2 护面块体选取及模型设计
试验护面块体采用扭王字块,考虑两种重量。为了研究斜坡堤不同坡度条件下的扭王字块失稳情况,斜坡堤取3种不同的坡度,具体参数如表1所示。由于本文直接针对的是模型块体,作为参考,表中给出了按1:50比尺换算的块体原型重量。根据相应的规范规定,试验中扭王字块的摆放方式为随机定点摆放1层[15]。

表1 物理模型试验采用的块体重量、摆放方式以及斜坡堤坡度Tab.1 Block weight, placement mode and embankment slope used in physical model test
试验典型断面形式如图1所示。针对下文所列波浪要素,为保证试验过程中不越浪,设计的斜坡堤堤顶高程为1.2 m,斜坡堤堤前水深为0.6 m。其中块石垫层采用(1/10~1/20)护面块体的重量。堤心块石参考实际防波堤,模型中采用0.6 g左右的石子模拟。
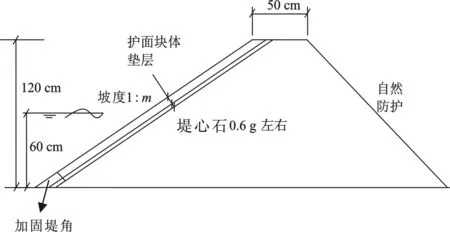
图1 斜坡堤试验断面结构图Fig.1 Section structure of slope embankment
斜坡堤摆放于距离造波板50 m处。斜坡堤后方摆放消能器,以减小反射波对于斜坡堤前入射波的影响,保证试验结果的准确性。需要说明的是,虽然水槽造波机具有主动吸收功能,但是考虑到较长周期波浪的非线性较强,对于主动吸收的效果有一定的影响。为防止波浪二次反射对于试验结果的影响,试验中将2.0 m宽的水槽分割为两部分,分别为0.8 m和1.2 m,模型布置在0.8 m宽的部分,1.2 m宽的部分不摆放模型,波浪可以传播至水槽末端的消能装置。
1.3 试验波浪要素
试验采用不规则波浪,依据有效波高Hs和有效周期Ts进行波浪的模拟,不规则波浪的频谱采用合田改进的JONSWAP谱[16],即
(1)
(2)
(3)
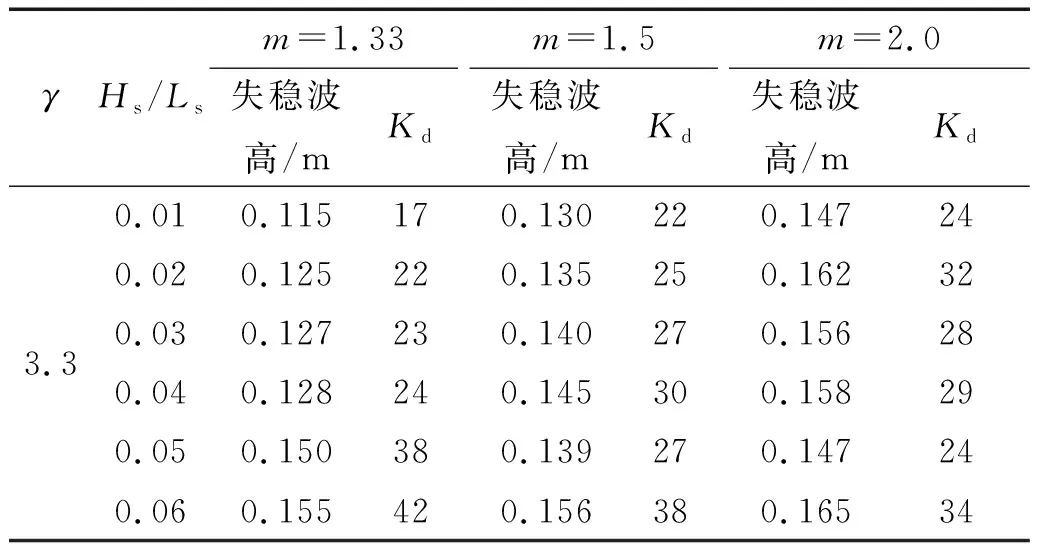
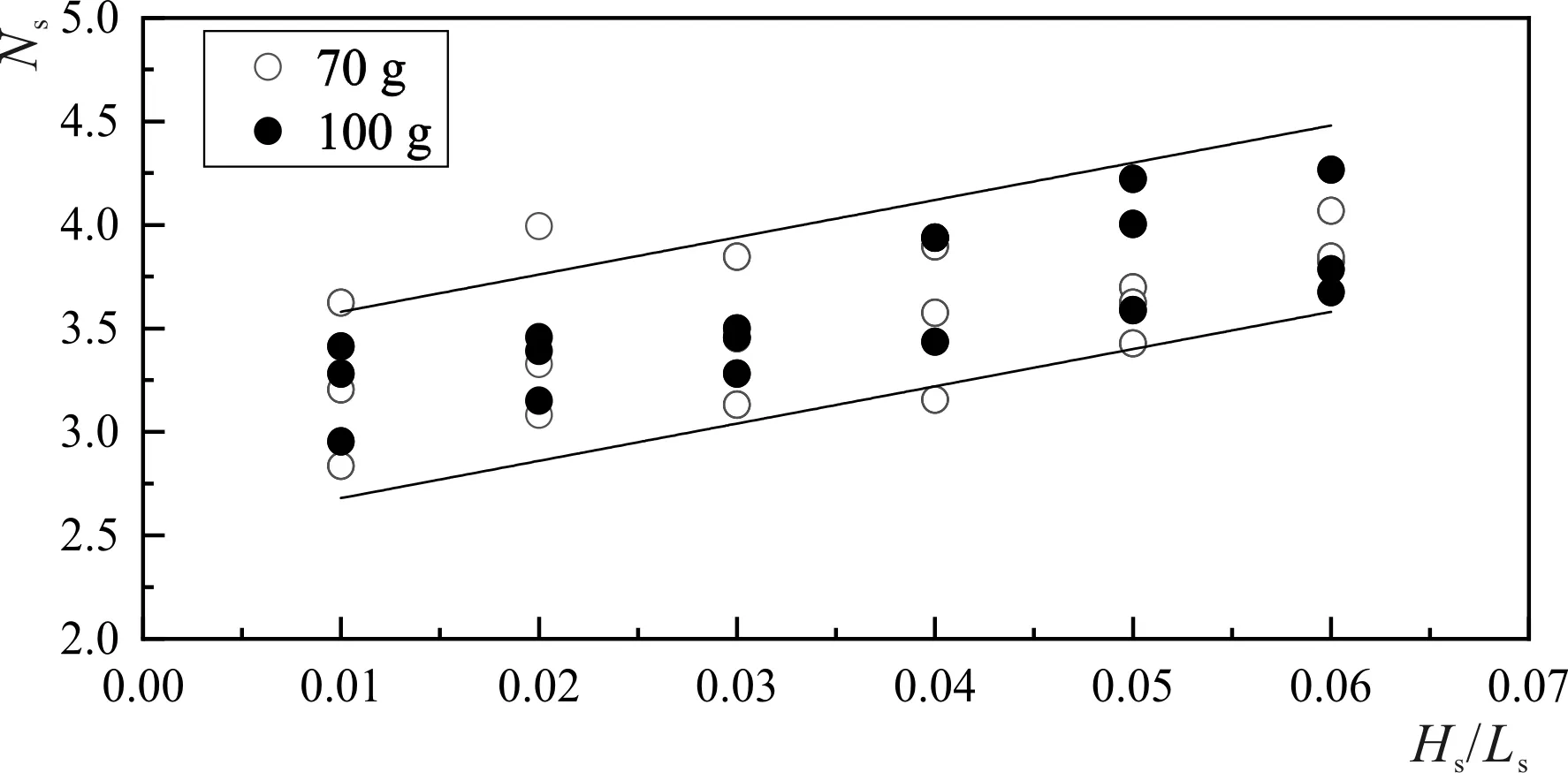
式中:σ=0.07(f 试验所用的波浪要素如表2所示。其中Ls为波浪有效周期所对应的深水波长。试验深水波陡Hs/Ls=0.01~0.06,波陡增量为0.01,针对每一级波陡,分别确定该波陡条件下块体失稳的波高和周期值,γ取3.3。 表2 物理模型试验波浪参数Tab.2 Wave parameters in physical model tests 在进行波浪对于斜坡堤作用试验时,考虑实际防波堤的破坏是一个大浪过程连续作用的结果,为了与实际波浪作用过程一致,每级波高的造波时间保证同时满足长于原型3 h和不小于连续1 000个波。同时,在进行每一级波陡波浪试验时,试验从小波做起,以便断面达到稳定状态。逐渐增大波高,直至在波浪作用下,防波堤的护面块体失稳。斜坡堤的护面块体由专人摆放,而且每次试验结束后,护面块体重新摆放。每次试验重复两次。 在波浪作用下,护面块体的失稳判断标准为,随机抛放的扭王字块的累积位移超过单个块体的最大几何尺度时即为失稳;另外,其发生位移后产生的缝隙宽度超过块体最大几何尺度一半时亦为失稳。 为了计算试验工况的块体失稳率,根据《防波堤设计与施工规范》[15],可以计算出各个坡度下,试验中斜坡堤模型所需要的块体数量,并由此得到静水面上下一个波高范围内的块体数量。从而可由下式计算护面块体的失稳率,即 (4) 式中:nd为失稳块体个数,N为所研究护面块体静水面上下一个波高范围内的块体数量。 图2和图3分别给出了70 g和100 g扭王字块在坡度为1:1.33、1:1.5和1:2.0的情况下,不同波陡波浪作用时,护面块体失稳率随波高的变化,其中图中的第1次和第2次表示试验重复次数。需要说明的是,为了清楚显示护面块体失稳率的变化趋势,图中纵坐标采用了对数坐标,最小坐标值采用0.01%,近似为0。从图2和图3中可以看出,护面块体的失稳率随波高的变化均呈现出类似的规律,即随着波高增大,护面块体失稳率增大。而且一般情况下,由于为单层块体,当有护面块体失稳后,块体失稳数量会快速增多,很快防波堤发生破坏。对每一种工况下,比较不同波陡条件下的扭王字块开始失稳的波高,可以看出,对于同一重量的扭王字块,失稳波高随波陡增大有增大的趋势,即波陡越小,失稳波高越小,护面块体越容易失稳。需要说明的是,一般情况下风浪对应的波陡较大,涌浪对应的波陡较小,即涌浪与风浪相比更容易导致斜坡堤护面块体的失稳。其主要原因是在斜坡坡度一定的情况下,波浪的波陡越小,波浪与斜坡作用时斜坡坡度相对于波浪越陡,波浪更倾向于卷破或激破,对于护面块体的冲击作用越大。 2-a m=1.332-b m=1.52-c m=2.0图2 70 g扭王字块在不同坡度的斜坡堤上不同波陡情况下的失稳率n随波高的变化Fig.2 Variation of instability rate n with different wave steepness on different slope of the embankment for 70 g accropode 3-a m=1.333-b m=1.53-c m=2.0图3 100 g扭王字块在不同坡度的斜坡堤上不同波陡情况下的失稳率n随波高的变化Fig.3 Variation of instability rate n with different wave steepness on different slope of the embankment for 100 g accropode 此外比较不同坡度的试验结果可以看出,对于同一重量的扭王字块,斜坡堤的坡度越陡,失稳波高越小。这一点与Hudson公式所描述的规律是一致的。 由于试验过程中选取的波高级别为0.02 m,且单层摆放扭王字块的允许失稳率为0%,因此试验得到的扭王字块开始失稳的波高并不是失稳率为0%的临界波高。因此,基于前面得到的扭王字块失稳率变化规律和趋势,可以近似估算出每一种试验工况下扭王字块失稳率n=0%时的临界波高。表3和表4分别给出了70 g和100 g扭王字块在不同坡度m及波陡Hs/Ls时对应失稳率n=0%的临界失稳波高以及基于《防波堤设计与施工规范》[15]规定的Hudson公式所得的Kd数。总体来讲,波陡越小,对应失稳率n=0%的临界失稳波高越小,Kd数越小,护面块体越容易失稳。另外,根据《防波堤设计与施工规范》[15]规定,扭王字块的Kd为18,试验所得大部分结果大于规范规定值,其原因可能是由于规范中的结果为在各种可能条件下的最不利结果。 表3 70 g扭王字块在不同m和Hs/Ls情况下对应n=0%的临界失稳波高以及按Hudson公式所得的Kd数Tab.3 The critical instability wave height and the Kd number according to Hudson′s formula for n=0% on the basis of different m and Hs/Ls for 70 g accropode 表4 100 g扭王字块在不同m和Hs/Ls情况下对应n=0%的临界失稳波高以及按Hudson公式所得的Kd数Tab.4 The critical instability wave height and the Kd number according to Hudson′s formula for n=0% on the basis of different m and Hs/Ls for 100 g accropode 为进一步分析波陡对于护面块体稳定性的影响,参考Hudson[4]公式,可定义稳定数Ns为 (5) 根据表3和表4所列分析结果,可以计算所定义的块体稳定数Ns。两种重量块体试验结果所得稳定数Ns与波浪波陡的关系如图4所示。从图中可看出,采用上述无因次参数,综合考虑坡度的影响,两种重量试验结果基本一致,块体的稳定系数Ns随着波陡的增大而增大,也就是说,若按Hudson公式计算,Kd数随着波浪波陡增大而增大。因此,在实际工程设计时,应考虑设计波浪的波陡对于护面块体重量的影响,波陡越小的波浪,所采用的护面块体的重量应越大。在进行试验过程中,采用了三种不同的斜坡堤坡度,因此可能造成图4中每级波陡各组次之间Ns数存在一定的差别。 图4 两种重量扭王字块体试验结果所得稳定数Ns随Hs/Ls的变化Fig.4 Change of stability number Ns with Hs/Ls from the test results of two kinds of weight accropode blocks 本文针对扭王字块,进行了斜坡堤护面块体的物理模型试验,研究了不同波陡和不同坡度对护面块体稳定性的影响,结论如下: (1) 对于同一重量的扭王字块体,失稳波高随波陡增大有增大的趋势,即波陡越小,失稳波高越小,护面块体越容易失稳。 (2) 对于同一重量的扭王字块体,随坡度变陡,失稳波高亦有减小的趋势,亦即斜坡堤的坡度越陡,护面块体越容易失稳。 需要说明的是,本文针对波陡对于扭王字块体稳定性的影响进行了试验研究。结果表明,波陡对于块体的稳定性具有明显的影响,扭王字块的稳定系数随波陡的减小而减小,即Hudson公式中的Kd数随波陡减小而减小,也就是说,波陡越小的波浪,所采用的护面块体的重量应该越大。需在实际工程设计时予以注意。
2 模型试验结果与分析
2.1 护面块体失稳率统计与分析

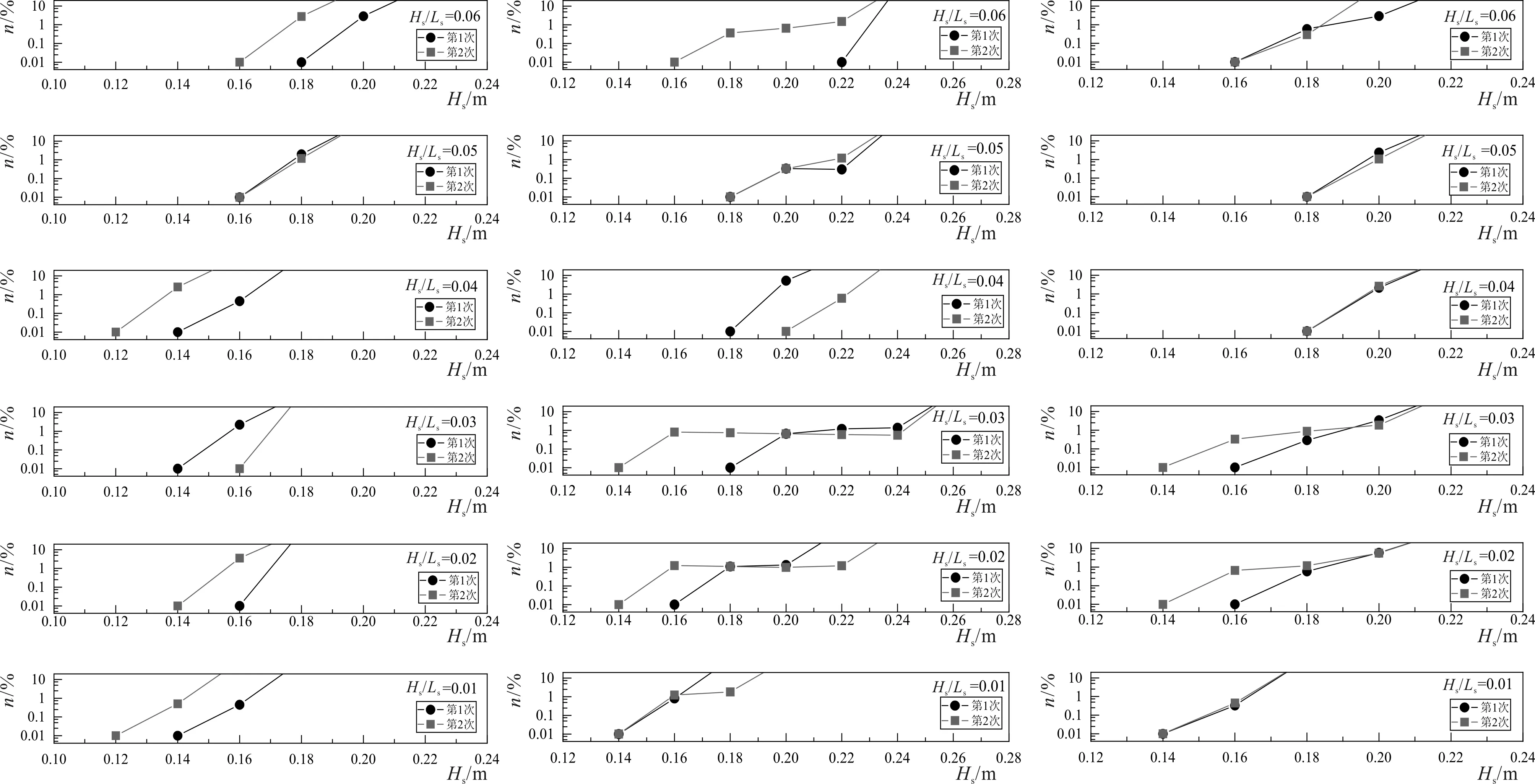
2.2 波陡对于护面块体稳定性的影响分析

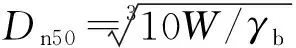
3 结论和探讨
