微型薄板直线压电电机的设计与性能研究

舒 嵘

（南昌航空大学 航空制造工程学院，南昌 330063）

引 言

压电电机是一种利用陶瓷元件的逆压电效应和界面间的摩擦耦合来实现宏观驱动的非传统作动器，具有结构紧凑、无电磁干扰、重量轻、断电自锁、响应快、精度高等优点，已成功应用于航天、精密制造、光学、医学、微电子器械等领域[1-5]。

直线压电电机作为压电电机的一种，由于其机构简单、设计灵活、输出力矩大，一直备受关注。自上世纪末，国内外研究人员就开始对直线压电电机的研究，其种类已有数十种之多。根据所利用振动模态，直线压电电机可分为夹心式和贴片式两种。夹心式直线压电电机利用压电元件的d33模态，学者们大多以大功率输出为目标进行设计，例如，Liu等[6]研制的U-型直线压电电机，其最大输出力可达40 N；Yun等[7]研制的大功率直线压电电机，其输出力最大达到92 N; Liu等[8]研制的单相驱动直线压电电机，可实现最大推力40 N，推重比达到33.3。Li等[9]研制的V-型直线压电电机，其输出力可达15 N，推重比为75。夹心式直线压电电机的输出功率大，但其体积相对较大，不易小型化。贴片式直线压电电机利用压电元件的d31模态，其结构更加紧凑，但输出力小，例如，范等[10]研制的模态复合直线压电电机，其最大输出力为3.4 N；Koc等[11]研制的空心圆柱形电机，直径2.4 mm，长10 mm，输出力矩1.8 mNm。对于一些精密的应用需求大多采用贴片式压电电机。然而，由于工作模态的原因，这些贴片式电机所使用的弹性体大多为块状金属，体积与质量相对较大。因此为了进一步减小电机的体积与质量，本文设计了一种微型薄板直线压电电机，该电机结构采用一阶面内弯振与一阶面外弯振耦合振动模态，结构更加简单。

本文将介绍所提出的电机结构与工作原理；拟运用COMSOL有限元仿真软件对其优化设计并对实验样机进行机械特性测试与性能评估。

1 电机结构及其工作原理

薄板直线电机结构如图1a所示，包括定子部分与动子部分。定子由四片同规格压电陶瓷和薄板金属弹性体组成，四片压电陶瓷分别粘贴于金属板两侧，极化方向沿厚度方向向内，如图1b所示。金属板一侧设有U形缺口，用于调节频率以及放置动子，其侧面用作驱动面。图1c为动子结构图，机体为U形碟簧，直接施加预压力，极大程度上简化了预压力施加装置。为提高耐磨度、减小电机工作时产生的噪声以及提高电机寿命，动子两侧分别粘贴摩擦材料，与定子两驱动面直接接触。另外，定子部分没有设计固定装夹点或者柔性固定脚，而是采用弹性装夹的方式，以最大程度降低电机的尺寸。

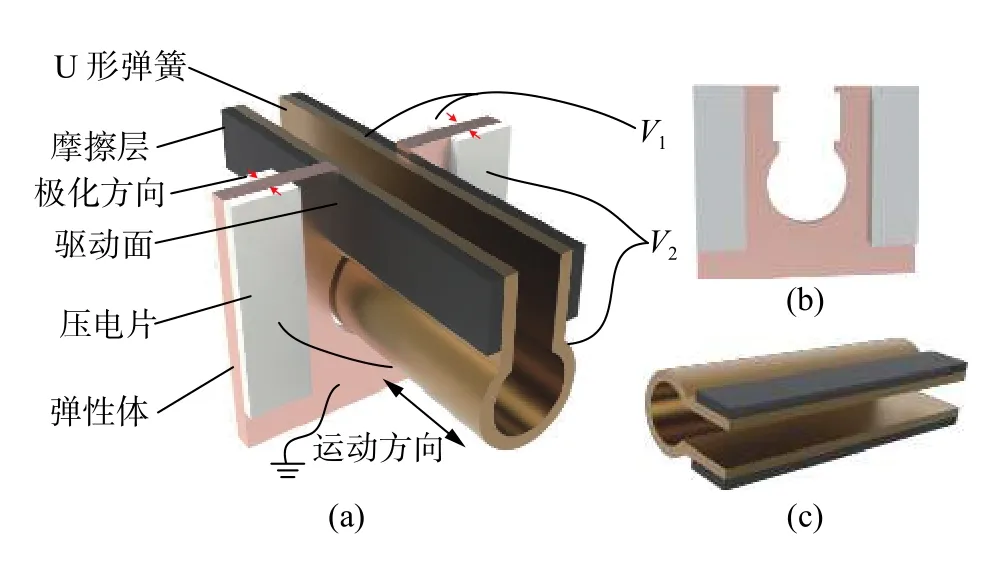
图1 微型薄板直线压电电机示意图

为了驱动动子直线运动，需要在定子两个驱动面处形成两个异向椭圆运动。因此，模态选择对电机性能有着重要影响。在驻波电机中，工作模态一般选取低阶振动降低电机的工作频率，以获得最小的损耗。本文中直线电机的工作模态为面外一阶弯振和面内一阶弯振，如图2a、图2b所示。通过优化设计将两模态频率调节一致，实现模态耦合。电机采用正弦电压激励，位于同侧的陶瓷片使用相同的激励电压，两侧的陶瓷分别以电压信号V1和V2的同时激励，如图1a所示。其中V1=Asin (wt)，V2=Asin (wt+θ)，A为电压幅值，w为激励信号角频率，θ为两激励信号之间的相位差。当定子以谐振频率激励时，两正交模态形成的耦合模态被激励出来，在驱动面处形成面外的椭圆运动，驱动动子宏观运动。当相位差为π/2时，动子正向运动；当相位差为−π/2时，动子反向运动。为了清晰的阐明定子驱动面形成椭圆运动的过程以及耦合模态的振型变化，将单个激励周期均分为t1～t4四个时间点，不同时刻所对应的振型如图3所示。

图2 振动模态

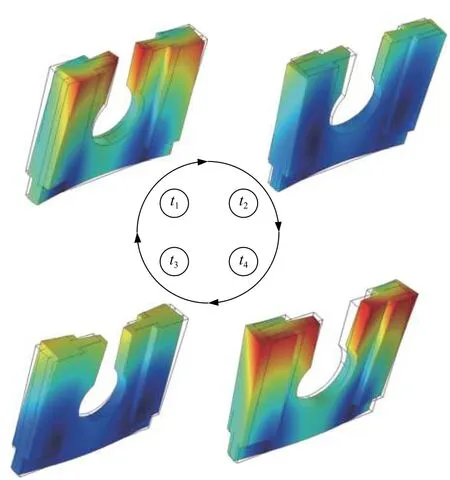
图3 单激励周期内直线电机的振型变化

2 有限元仿真

本文设计的压电电机包含面内和面外两个一阶弯振模态，设计此类电机时应考虑以下几个因素：1）定子的两种工作模式应在超声频率范围内；2)这两种模态的固有频率应尽可能接近。文中选用磷青铜QSn作为金属弹性体的材料，压电陶瓷采用PZT-8，材料参数如表1所示。定子结构如图4所示，初始参数l1= 5 mm、l2=l1− 1、w1= 6 mm、w2= 1 mm、r= 1 mm、d1= 2 mm、d2= 2 mm、d3=0.3 mm、t1= 0.5 mm、t2= 0.3 mm，其中需要优化参数为金属板长l1、宽w1、压电片宽w2、中间孔径r1。有限元模型基于COMSOL多物理场仿真软件建立，模型网格如图5所示，相对于实际定子模型中对于尺寸较小的参数做出简化：1）忽略压电陶瓷于弹性体之间的胶层；2）忽略驱动面的深度，即参数d3。

表1 材料参数

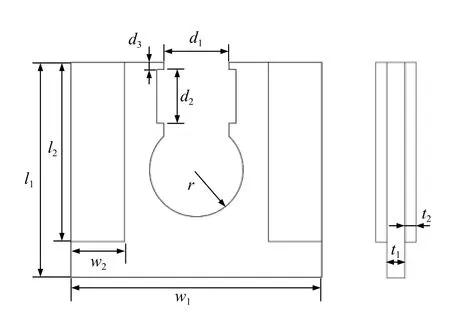
图4 定子结构参数

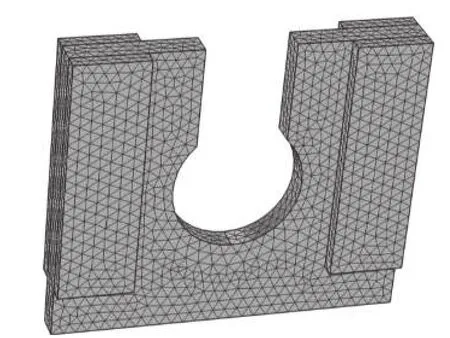
图5 定子有限元模型网格划分

本文采用短路电边界条件进行模态分析。初始参数下定子面内一阶弯振和面外一阶弯振频率为26 955 Hz和28 533 Hz。然而，要使两个弯曲模态的模态频率应尽可能接近需要对其尺寸进行优化设计。为解决两种工作模式频率一致性调节问题，以参数的灵敏度为指导，调整结构参数，减小两种运行方式的频率差。同时还可以参数对频率的灵敏度确定加工公差，以减小尺寸误差。灵敏度的相应表达式如下所示[12]：

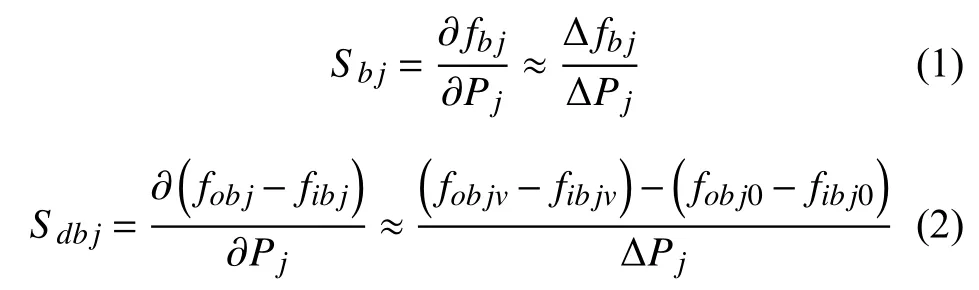
其中，Sbj为结构参数相对频率的灵敏度，ΔPj为结构参数相对于初始值的变化，Δfbj为频率变化值；Sdbj为频率差灵敏度，fobj和fibj分别为面外和面内一阶弯振频率变化值。

通过对不同结构参数的模型进行模态分析，计算出结构参数的灵敏度，通过归一化处理得到结果如图6所示。图中所示，对频率和频率差影响最大的参数为w1和r，因为这两个参数w1的增大会增加结构的刚度，而r的增加会大大减小结构的刚度。

图6 结构参数灵敏度

最终优化后的结构参数如表2所示，其面内模态和面外模态频率分别为20.554 kHz和20.416 kHz，频率差为138 Hz。

表2 优化后结构参数

为研究定子的振动特性，通过向压电陶瓷施加电压对定子进行谐波响应分析，电压施加方式如图1所示，电压幅值为200 Vp-p。通过谐响应分析得到20.4、20.46、20.5、20.6、20.7 kHz五个频率下的驱动轨迹如图7所示。驱动面的椭圆轨迹的形状影响电机的性能，而运动轨迹直接可以受到电机频率的控制。因此可以通过改变激励频率来调控电机。

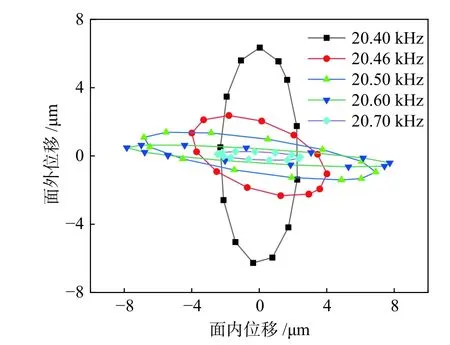
图7 驱动面中点振动轨迹

3 动子设计

在以摩擦驱动原理工作的压电电机中，提高输出性能除了对定子的优化设计之外，最重要因素是定子和滑块之间的预紧力。动子结构如图1c所示，由摩擦材料和U形碟簧组成，其预压力施加方式如图7所示。将动子插入定子孔时，会向动子两侧摩擦材料施加外力使得U形碟簧变形产生反向的预压力。为使动子顺利插入定子U形槽，避免多余接触，动子的尺寸略小于定子的槽的尺寸。

U形碟簧产生的预压力可根据弹簧中存储的应变能进行估算。U形碟簧可看做对称的悬臂梁，其变形主要为圆形悬臂，忽略固定摩擦材料平面的变形，碟簧壁厚h=R2−R1，长度为L。悬臂梁上某点的力矩M为可表示为：

其应变能可表示为：

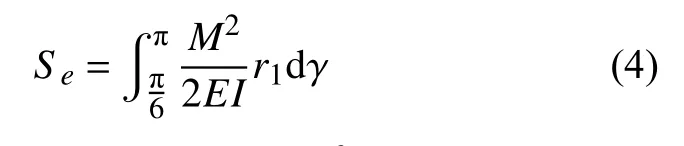
其中，E为动子弹性模量，v为泊松比。

根据卡氏定律[13]，U形碟簧的应变可以表示为：

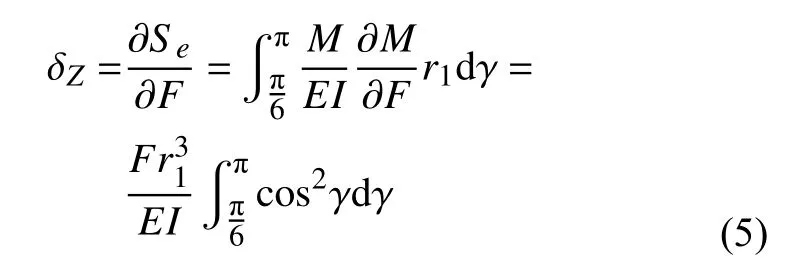
从图8中可以得到δZ=R1-r1，将其带入公式（5）即可得出预压力值F。

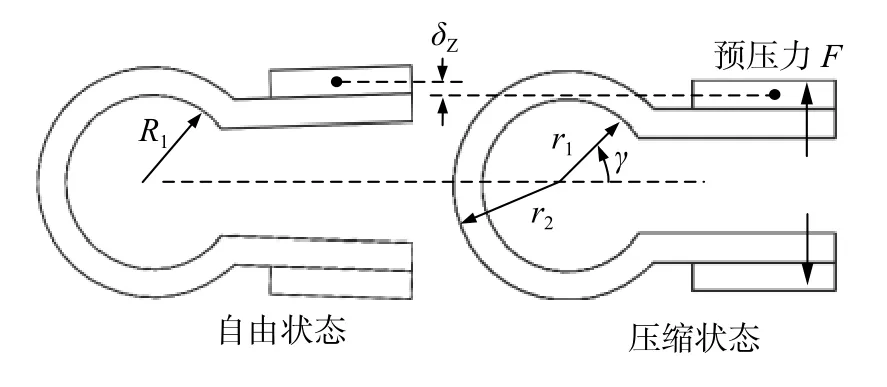
图8 预压力施加方式

4 实验研究

根据初步的仿真结果制作了样机模型，如图9所示。定子以厚度为0.5 mm的磷青铜板，通过激光加工而成，最大程度的减小了加工误差。定子质量为0.21 g，动子U形弹簧为磷青铜，厚度为0.2 mm，长度11 mm，摩擦材料为聚四氟乙烯，动子整体质量为0.12 g。动子开口缝隙为1.8 mm，底端圆形直径为2.1 mm，因此其开口角度γ约为30°。为了改变定子的预压力，准备了多个具有不同初始半径R1的动子。

图9 微型薄板直线压电电机定子原型和和试样样机

为测试定子的振动特性，文中采用具有非接触式振动测量和多点扫描功能的激光振动测试设备（Polytech PVF300）进行模态测试。幅频特性曲线如图10所示，面内一阶弯振和面外一阶弯振的频率分别为20.174 kHz和19.89 kHz，两频率差仅为284 Hz。由于有限元模型中没有考虑粘贴层的影响以及材料参数误差因素，测得的频率均低于模拟值。在有限元模型中，压电元件和金属元件的节点是刚性固定的。然而，这两个部分在原型中是用树脂粘合在一起的，这使得原型的刚度比有限元模型小。

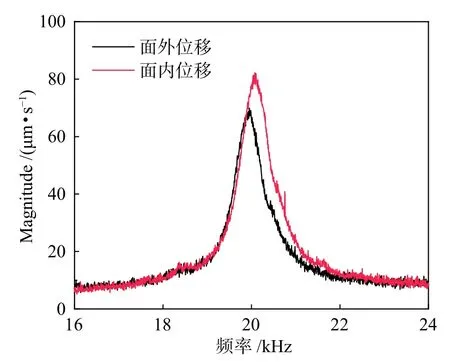
图10 样机幅频特性

为研究电机的输出特性，对其进行载荷特性试验，激励电压为两相相位差为90°的正弦电压，如图11方式进行激励，电压幅值为200 Vp-p，频率为20.06 kHz。采用非接触式激光位移传感器测量动子运动速度。为改变预压力，制作了4个初始直径为2.13，2.124，2.16，2.19 mm四种尺寸的动子，其对应的预压力分别为0.05，0.15，0.3，0.45 N。

图11 电机性能测试平台

电机的输出特性测试结果如图12所示，当预压力为0.15 N时可以使速度达到最大43 mm/s，而预压力在0.3 N时输出力达到最大5.3 mN。

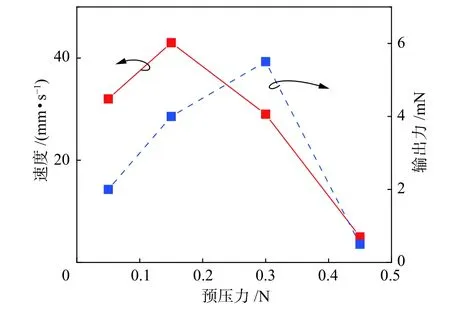
图12 电机输出特性

5 总 结

本文设计了一种微型薄板直线压电电机，电机采用面内和面外两个正交的一阶弯振作为工作模态，以获得较小的介电损耗。文中详细分析了该电机的工作原理以及激励方法。电机采用U形碟簧作为动子并通过自身弹性变形提供与压力。利用商用有限元软件COMSOL对定子进行了仿真优化设计。为验证上述电机工作原理，加工了样机并进行测试。该电机定子质量仅为0.21 g，实验结果表明，在200 Vp-p激励电压、0.3 N预压力下可以提供5.3 mN输出力。此外，本文提出的直线压电电机体积小，质量轻，在微纳卫星等空间高性能需求设备中具有巨大的潜在应用价值。