非均匀光照下阵列的改进配置分析
2021-11-20罗秀英雷国平朱海涛
罗秀英,雷国平,邓 立,朱海涛,蔡 黎
(1.重庆三峡学院电子与信息工程学院,重庆 404130;2.葛洲坝能源重工有限公司光伏光热事业部,北京 100102)
光伏发电检修方便、清洁、无污染[1],局部阴影下存在功率失配的问题,据统计,局部阴影造成的损失是各类商业用光伏电池的70%[2],为了减少功率损失,许多学者对光伏阵列的配置进行了研究。文献[3]提出了空间向量法,将受光照强度相当的组件进行串联,通过改变阵列结构来提高输出功率,但是该方法增加了开关和微处理控制器,即增加了成本。文献[4]提出自适应重构方法,利用开关矩阵的闭合将阴影遮挡下的组件移除,同时对其进行额外补偿,该方法比较极端,浪费了阴影下组件的输出功率。文献[5]在进行仿真时,所有的模块温度均设置为理想工作温度25 ℃,在8 种阴影模式下研究串联(series:S)、串并联(series and parallel :SP)、桥连接(bridgelinked:BL)和蜂窝(honey comb:HC)配置的性能,最后得出HC的性能更优。文献[6]以Matlab 系统中自带的光伏组件进行仿真,模拟5×5 光伏阵列在25 ℃的恒定温度和不同光照强度下运行,与S 和SP 系列光伏阵列配置相比,HC 光伏阵列配置是产生最大功率的最合适的光伏阵列配置。文献[5-6]均在实验时将模块温度设置为恒定值25 ℃,没有考虑到光照强度对模块温度的影响。
本文在不增加成本和组件复杂度的基础上,对阵列配置进行优化,且充分考虑光伏板温度变化,并通过与传统的阵列算法进行功率电压(P-U)特性比较分析,得到SP-HC 阵列配置是最优配置的结论。
1 传统配置
1.1 工作原理
电池是组成光伏阵列的基本单元,光伏电池的I-U特性数学模型如式(1)所示:
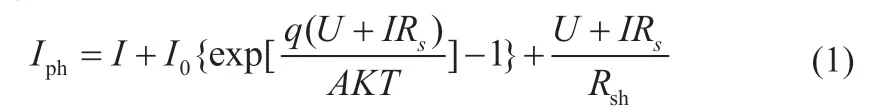
式中:I为光伏电池实际输出电流;U为光伏电池实际输出电压;Iph为光生电流,通过计算Iph=(G/G0)IG0得到,其中G0取1 000 W/m2,IG0是标准测试条件(STC)下的光生电流,G是组件表面变化的光照强度(W/m2);I0为反向饱和电流;A为二极管特性因子;K为玻耳兹曼常数,1.38×10-23J/K;q为电子电荷量,1.6×10-19C;Rs为串联电阻;Rsh为并联电阻;T为组件实际温度,通过计算T=Tair+kG得到,其中Tair是组件实际所受环境温度,k取0.028 75(℃·m2)/W。
单个电池的输出功率不符合工程实际,因此需将光伏电池串并联后得到较高的输出电压与电流。光伏组件数学模型由式(1)的光伏电池数学模型演化而来,如式(2)所示:

式中:Ni为光伏电池串联数;Nj为光伏电池并联数。传统光伏阵列主要有SP、BL、HC 配置方式,其详细功率计算过程参考文献[7]。
1.2 主要参数指标
衡量光伏阵列性能优劣的参数主要有填充因子(FF)、最大失配功率损失(MMPL)。不同配置下阵列FF的值越高,阵列的光电转换效率越高,其中FF的计算如式(3)所示;MMPL是均匀照射和局部阴影照射下功率的差值与均匀照射下最大功率的比值,如式(4)所示,不同配置下阵列MMPL的值越高,阵列的光电转换效率越低。

式中:Isc为短路电流;Voc为开路电压;Pm为电池最大输出功率;PGMPP,U为均匀光照下的最大功率;PGMPP,PSC为局部阴影下全局最大功率。
2 改进配置
为了进一步提高SP、BL、HC 结构下的阵列输出功率,在传统配置的基础上结合HC 与SP 配置,提出一种新的配置记为SP-HC,如图1 所示,组件的U-I特性用式(5)表示。
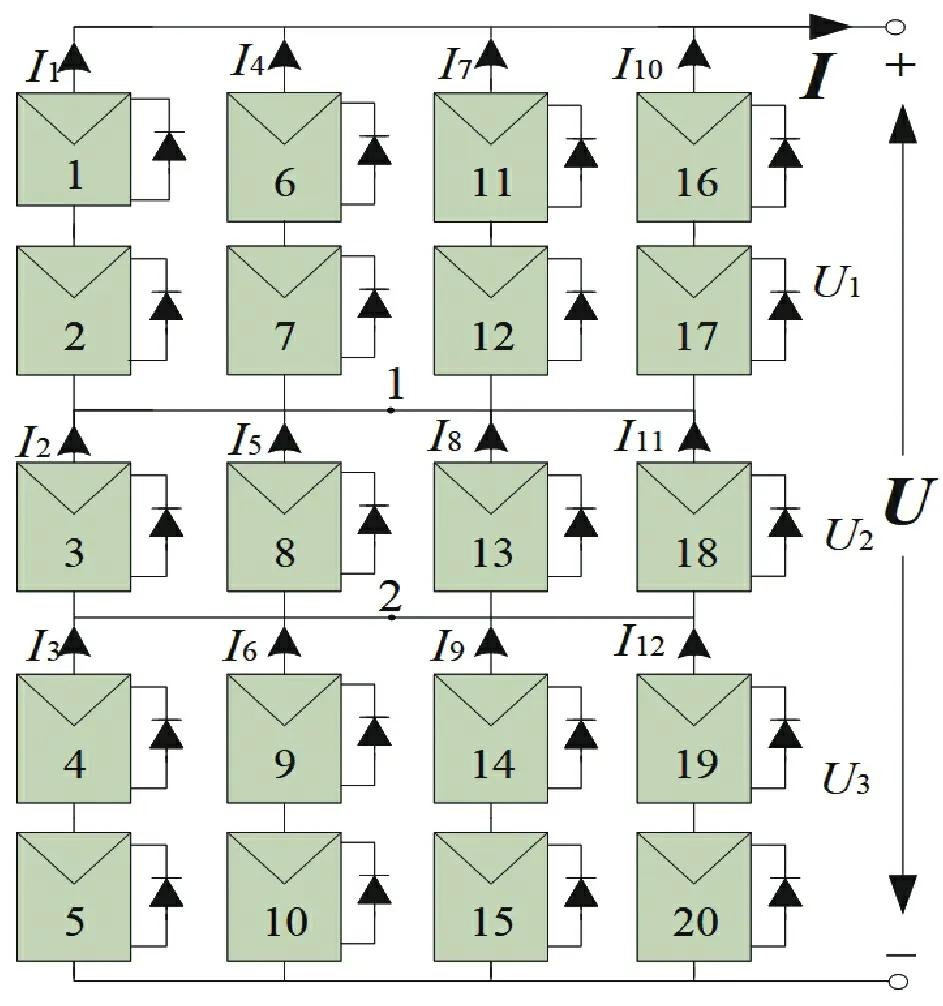
图1 新型光伏阵列结构

式中:i为光伏电池板的组件编号;Ix为各支路的电流;Gi为对应组件编号的光照强度;Uy为组件第y(1≤y≤3)行的行电压,新型配置的实际输出电压为3 行输出电压的总和,如式(6)所示。根据图中的结点2、3 列间的2 个节点,基于基尔霍夫定律(KCL)得到式(7)。

此结构的表达式中共有15 个未知量,包括12 个电流值和3 个电压值,需要公式(5)提供的12 个表达式、公式(6)提供的1 个表达式以及公式(7)提供的2 个表达式联合求解。本文总结了传统阵列配置的计算复杂度与新型结构的计算复杂度,如表1 所示,从表中的计算复杂度可知,新型配置的计算最简单,其次是SP 结构,BL、HC 配置的计算最复杂。

表1 不同阵列配置下计算复杂度
3 不均匀光照下阴影分布
光伏阵列所受的局部阴影主要分为集中式和分散式两大类,集中阴影又分为渐变和不渐变两种。以6 种不同的局部阴影模式为例进行研究,位于左上角的渐变阴影记为阴影1、分散阴影记为阴影2、位于左上角的非渐变阴影记为阴影3、位于对角线上的渐变阴影记为阴影4、位于对角线的非渐变阴影记为阴影5、位于下方的非渐变阴影与位于右边的渐变阴影组成的L 形阴影记为阴影6,阵列所受阴影分布如图2所示。
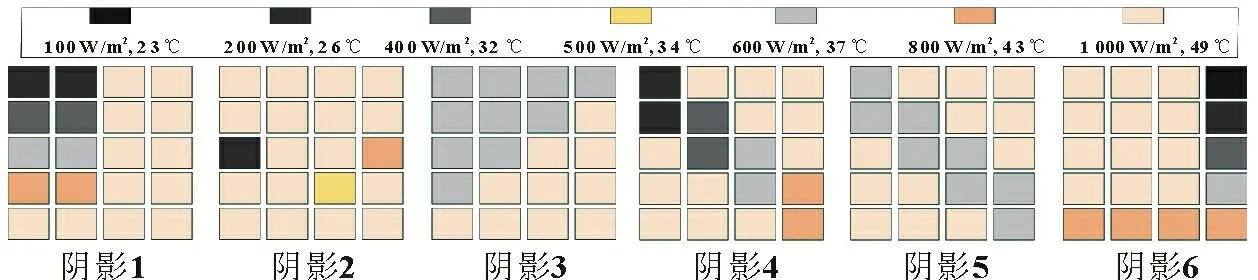
图2 光伏电池板上局部阴影分布
4 仿真与结果分析
4.1 仿真环境
在2016a 版本的Matlab/Simulink 中搭建由400 个相同的光伏电池片组成的5×4 光伏阵列发电模型,阵列中所用到的光伏组件在STC 下的参数如下:Rs=0.10 Ω,Rsh=82.12 Ω,Iph=8.63 A,I0=6.44×10-5A,A=0.99,光伏组件开路电压的温度系数为-0.339 69 %/℃,短路电流的温度系数为0.063 701 %/℃,STC 下四种不同结构的阵列P-U特性曲线如图3 所示,其最大功率均为1 689 W,验证了新型配置模型的正确性与有效性。

图3 STC 下四种不同结构的阵列P-U特性曲线
4.2 仿真结果
由于局部阴影的形状与形成位置的不同,光伏阵列输出的功率也不相同。不同阴影下,仿真图中用不同的颜色与线型表示了不同阵列结构的功率变化,如图4~9 所示。图10 给出了不同阴影下不同配置的阵列FF值与MMPL值,横轴用阵列配置类型-阴影类型的简写表示,通过分析P-U特性和FF、MMPL的值的大小可以得到如下结论:

图4 阴影1下各结构的P-U特性曲线

图5 阴影2下各结构的P-U 特性曲线

图6 阴影3下各结构的P-U特性曲线

图7 阴影4下各结构的P-U 特性曲线

图8 阴影5下各结构的P-U特性曲线

图9 阴影6下各结构的P-U特性曲线

图10 不同阴影下不同结构阵列的MMPL值与FF值
(1)功率随电压的变化而变化,不均匀照射下,功率曲线存在多个局部最大值,根据式(7)可知,当光伏发电系统工作电压未处于最大功率点电压时,输出功率不是全局最大功率,则会造成填充因子减小,降低功率输出;
(2)通过比较不同配置下全局最大功率值的大小,本文提出的新型配置在不同的阴影下性能均优于传统配置,即SPHC 配置下输出的功率最高,进一步比较阵列BL 配置与HC配置下的输出功率,得到BL 配置下输出功率较高;
(3)改进配置可以有效提高阵列的输出功率,均匀光照下光伏阵列的短路电流为35.05 A,开路电压为57.71 V,最大功率均为1 507 W,其填充因子为74.50%,但是在非均匀照射下,传统配置的FF值远远低于74.50%,由于FF值越大,阵列的输出功率越大,通过分析图10 中MMPL值与FF值的大小,可知SP-HC 配置在传统配置的基础上将FF值平均提高了4.32%,将MMPL均降低了4.62%。
(4)当阴影为对角不渐变阴影时,SP-HC 配置提升功率最明显,将SP 配置下的FF值提高了11.23%,MMPL降低了11.61%,因此针对该阴影类型可优先选择SP-HC 配置。
5 结论
本文主要研究了提高光伏阵列输出功率的方法,通过改进阵列的传统配置,得到了一种计算简单且光电转换效率得到提升的新配置方式,即SP-HC 配置。以Soltech 公司提供的参数为例,对新型配置与光伏阵列的传统配置进行仿真分析,在充分考虑了光照强度对电池板的实际温度影响的情况下,仿真结果表明在SP-HC 配置下,阵列的功率输出高于传统配置的功率输出,即SP-HC 配置为光伏阵列的最优配置。
对于如何保持阵列始终输出最大功率,则需要对最大功率点进行最大功率点追踪(MPPT),因此MPPT 算法的优化是提高光电转换效率的一大研究方向[8],后面的研究将在光伏阵列最优配置基础上对MPPT 算法进行改进。
