BaCl分子的基态和激发态的光谱和分子常数

2021-11-20伍冬兰袁金宏王玲娣马睿华刘珊珊

井冈山大学学报(自然科学版) 2021年5期

伍冬兰，辛霞，袁金宏，王玲娣，马睿华，刘珊珊

*伍冬兰，辛霞，袁金宏，王玲娣，马睿华，刘珊珊

（井冈山大学数理学院，江西，吉安 343009）

利用Davidson修正的内收缩多参考组态相互作用(ic-MRCI+Q)方法，优化计算了BaCl分子基态和激发态的势能曲线。为了得到更加精确的结果，计算中借助了核价电子相关和相对论效应修正，然后利用修正的势能曲线，采用LEVEL8.0程序拟合得到相应的光谱常数、振动能级和分子常数。本次计算得到的光谱数据对今后进行BaCl分子的光谱实验研究具有重要的参考作用。

BaCl分子；MRCI+Q；光谱和分子常数；振动能级

0 引言

碱土金属卤化物在实际生活中有着广泛的应用，加上其具有特殊的电子排布，一直备受很多实验和其他理论学家的欢迎，因此对于BaCl的电子结构和光谱性质的研究较多。1989，年Ma等[1]用CASSCF（the complete active space self-consistent-field )的方法研究了BaCl低电子态X2Σ+，A’2Δ和A2Π的电子结构，给出了光谱常数(e，e，ee，e)。1993年，Launila等[2]记录了Ar+激光线在514.5nm处诱导BaCl分子的D2Σ+-X2Σ+和E2Σ+-X2Σ+转变的近紫外辐射，并且对这两个体系的(0，0)和(1，0)带进行了旋转分析，并得出了以上电子态的分子常数。Gustafsson等[3]采用近红外傅里叶变换光谱分析了A2Π和X2Σ+态的跃迁特性，获得了光谱和分子常数等。Amiot等[4]采用激光诱导荧光，结合高分辨的傅里叶光谱学研究了前七个电子态的光谱特性，并给出了部分光谱和分子常数。Berg等[5]利用激光诱导等离子体法测量了BaCl的零压辐射寿命。之后，由于BaCl+阳离子具有被冷却到超低温的潜力，因此备受关注。Joshua[6]通过脉冲场电离-零动能光电子光谱已被用于观察BaCl+的v=0-3振动水平，并提供了BaCl分子的电离能和振动常数的准确值。Robert[7]根据分子能量特点，利用激光冷却的方式进行振动分析，并改进了BaCl+分子基态X1Σ+的振动常数。

近年来，人们对激光冷却二原子极性的兴趣越来越大，激光冷却分子的应用也越来越多，因此激光冷却的方法得到了广泛采用。其中碱土金属卤化物分子由于其光谱的特殊性，再加上Franck-Condon因子较大且具有高对角性，被认为是激光冷却的候选分子。Yang等[8]采用多组态相互作用方法，结合赝势基分析了BaCl分子基态X2Σ+和第一激发态A2Π激光冷却特性，给出了X2Σ+1/2和A2Π1/2态的光谱参数和辐射寿命等。综合分析前面的理论计算结果发现，采用相关修正势能函数获得光谱常数的较少，而对包涵重元素Ba的分子体系，相对论效应对能级的排布影响非常明显。因此在计算光谱常数、振动能级和分子常数时尽可能要考虑相关修正。

本研究利用内收缩多参考组态相互作用方法(ic-MRCI)的计算方法，考虑相关修正精确计算了BaCl分子的基态与激发态的势能函数与光谱常数，再采用LEVEL8.0[9]程序拟合得到各个电子的光谱常数、振动能级和分子常数。这些理论数据对于理解此分子和开展光谱实验测量都具有重要意义。

1 理论方法

在本文所有的计算中，BaCl分子的所有电子结构以及与能量相关的计算均使用的是MOLPRO2012.1软件包[10]内完成的。通过测试多组不同的原子基组，进而选取一组最优的基组相对论有效芯赝势基(aug-cc-PV5Z-PP)作为Ba原子和相关一致基(aug-cc-pwCV5Z)作为Cl原子的计算基组。

BaCl分子是属于C∞v点群。因为受MOLPRO程序自身的局限性，所以目前本研究中涉及到的运算都仅仅是采用了C∞v点群中的Abelian群C2V点群来代替进行计算的。C2V群不可约可以表示为(A1/B1/B2/A2)，而C∞v群中的不可约可以表示为Σ+=A1，Π=B1+B2，Δ=A1+A2，Σ-=A2。在对BaCl分子的计算中，选择了8个分子轨道作为活性空间，它们分别对应Ba原子的6s5p轨道，Cl原子的3s3p轨道。对于BaCl，这些活性空间也是(4，2，2，0)，而剩余的其它电子被冻结。通过多参考组态计算方法MRCI考虑了价电子之间作用，为了计算结果更为严谨，使用Davidson修正对能量大小不一致性进行了校正，计算得出BaCl的势能曲线，然后通过编制程序包进行拟合得到光谱常数(e，e，ee，e，e)。通过势能曲线，借助LEVEL8.0程序包找到所有的振动电子态，计算出了振动能级v，惯性转动常数ν，以及离心畸变常数ν，最后给出了BaCl分子的电偶极矩变化关系图。

2 计算结果及讨论

2.1 束缚态的势能曲线和光谱常数

图1显示了BaCl分子X2Σ+和A2Π态的势能曲线，这是在无自旋的MRCI+Q水平上研究得到的。在图1中，取X2Σ+最低点能量为零，此时=0.28 nm，结果与Yang等[8]的理论研究结果符合较好，同时与同一主族BeCl[11]、MgCl[12]、CaCl[13]、SrCl[14]等分子的势能曲线也非常相似。表1中总结列出了BaCl分子X2Σ+和A2Π态的光谱参数，还包括以前的实验数据和理论结果。从表中可以看出，在误差允许的范围内，本文得出的计算结果较好。对于基态X2Σ+，比较本文的计算值与表1列出的实验值[3-4]，e、e、ee、e的差分别为0.0136 nm、14.45 cm−1、0.0553 cm−1、0.0079 cm−1，与表1理论值[8]比较的差仅为0.009 nm、1.94 cm−1、0.0753 cm−1、0.0053 cm−1。从表1还可以知道BaCl分子X2Σ+态的离解能e为4.588 eV，而同一主族元素分子SrCl[14]和MgCl[15]的离解能分别是3.703 eV、3.325 eV，可以得出BaCl分子的解离能比较大，说明该分子更难分离、更稳定。而对于A2Π态，e、e、e、ee、e的结果与表1中的实验值[3-4]更接近，其差值分别为57.9 cm−1、0.0092 nm、0.16 cm−1、0.2672 cm−1和0.0053 cm−1，与表1 理论值[8]的差分别为61 cm−1、0.0141 nm、3.74 cm−1、0.2772 cm−1和0.0052 cm−1。从以上数据分析发现，结果与实验值和理论值相差都不大，有些结果更接近实验值，说明本研究采用的计算方法和相关修正是合理可靠的。

图1 BaCl分子基态与激发态的势能曲线

表1 XΣ和AΠ态的光谱常数

Table 1 Spectral constants of the XΣ and AΠ states

Λ-S态Te/cm−1Re/nmωe/cm−1ωeχe/cm−1Be/cm−1De/eV X2Σ+00.2818265.440.86530.07614.588 理论【1】00.3024356.1316.57-- 理论【8】00.2728267.380.790.0814- 实验【3】0-279.890.810.0840- 实验【4】00.2682279.910.81-- A2Π105960.2824257.591.07720.07583.249 理论【1】8714.70.3049343.8271.78-- 理论【8】106570.2683261.330.800.0810 实验【3】10539.10.2732257.750.81-- 实验【4】10679-257.300.810.0811-

2.2 束缚态的振动能级和分子常数

在本文计算中，采用MRCI+Q方法对BaCl分子优化计算得出势能函数，借助于 LEVEL8. 0程序包，找到基态X2Σ+与激发态A2Π相关的所有振动态，然后给出了X2Σ+和A2Π态对应10个振动态的振动能级v，惯性转动常数v，以及离心畸变常数v，结果列于表2。由于到目前为止，很少相关的分子常数的实验和理论值，通过前期调研发现，文献[4]中X2Σ+和A2Π的0-0惯性转动常数v和离心畸变常数v实验值分别为0.083967 和3.00964*108cm-1, A2Π的分别为0.081054和3.23789*108cm-1，与本文的计算值吻合较好，相对误差分别为2.3%和3.1%，0.5%和2.4%,说明采用高精度计算方法和相关修正获得激发态的分子常数是可靠的，可以为今后的实验提供参考。

表2 BaCl 分子XΣ和AΠ的G、B和D值

Table 2 The G, B and D values of the XΣ and AΠ states for BaCl molecules

v0123456789 X2Σ+Gv/cm−10263.54525.47785.821044.431301.231556.311809.762061.502311.26 Bv/cm−10.0820010.0817110.0814170.0811420.0808450.0805410.0802420.0799510.0796500.079335 108Dv/cm−12.9159372.9239912.9324892.9526812.9671712.9719612.9771842.9955533.0514543.044252 A2ΠGv/cm−111365.5411619.9011872.6812123.4512372.2912619.4012864.6913107.8013348.9213588.04 Bv/cm−10.0806350.0803010.0799730.0796340.0792970.0789650.0786290.0782960.0719850.071617 108Dv/cm−13.1597793.1602793.1874953.1979523.2038673.2143843.2799643.2912883.3002653.350706

2.3 束缚态的电偶极矩

由于电偶极矩表示的是正电荷与负电荷分布的分离情况，所以本文计算得出了X2Σ+和A2Π态的电偶极矩在图2中列出。从图中可以看出，电偶极矩随着分子间距增大也跟着变化，两个态都呈现先增大后又逐渐减小的变化趋势，都存在一个最大值，当分子核间距增大到一定值时，电偶极矩减小趋于零，即只有当形成分子的两个原子间距足够远时，电偶极矩才为零，此时分子离解成原子。本文所得出的结果与文章SrCl[11]分子相比较，对于X2Σ+和A2Π两个态而言，电偶极矩变化曲线形状非常类似。我们的计算结果可为今后更多关于BaCl分子跃迁特性的研究提供参考。

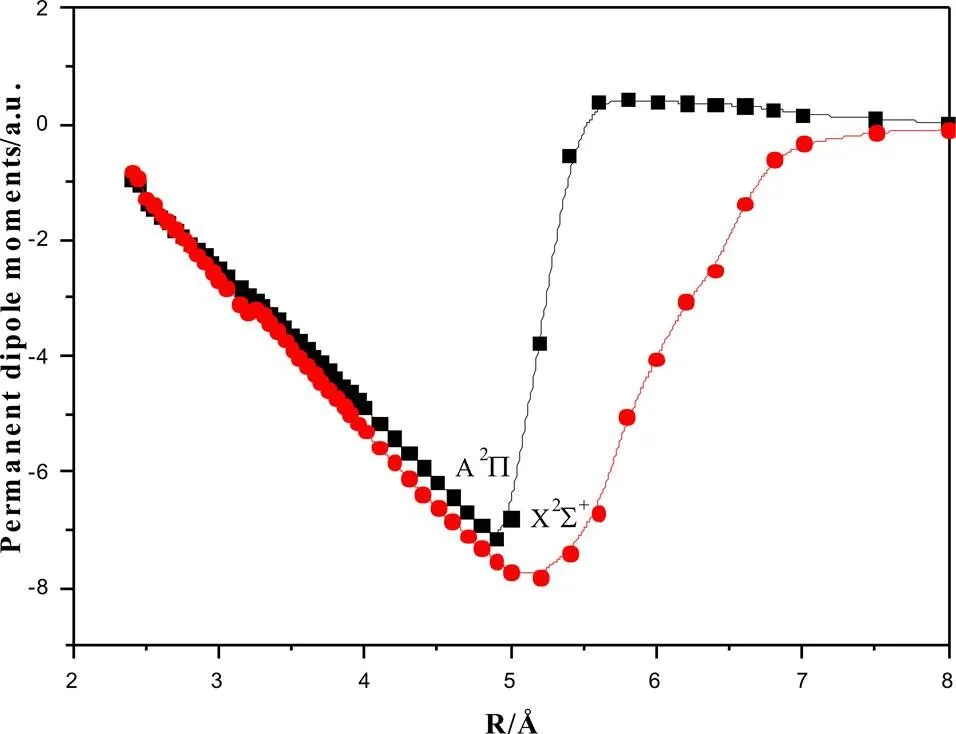
图2 BaCl分子基态与激发态的电偶极矩

3 结论

利用高精度的MRCI+Q计算方法，考虑Davidson能量大小一致修正，通过分析，结果表明，我们计算得到的BaCl分子基态与激发态的势能曲线和光谱常数与现有的实验数据更接近，与近年来的理论研究也吻合得较好。从两个态的势能曲线图来看，对于不同的电子态离解极限不同，离解能也不一样，图中还可以看出每个态都存在较深的势阱，说明分子基态和激发态都比较稳定；从电偶极矩变化关系图也可以看出，存在较大的电偶极矩值，也说明这两个态比较稳定，与势能函数得出的结论是一致的。文章中还给出了10个振动能级、转动常数等分子常数，有的误差很小，可以作为光谱实验参考。本文计算所提供的数据对于钡卤化物激光冷却的可行性分析也可以提供较好的数据参考。

[1] MaZ X, DaiS S. Electronic structure of BaCl [J]. Chemical Physics Letters, 1990, 166(4):404-407.

[2] Launila O, Royen P, Zackrisson M, et al. Rotational analysis of the D2Σ+-X2Σ+and E2Σ+-X2Σ+band systems of BaCl [J]. Molecular Physics, 1993, 78(3): 763-767.

[3] Gustafsson G, Gustavsson T, Martin H. Fourier transform spectroscopy of the near-infrared A2Π-X2Σ+transition of BaCl [J]. Journal of Molecular Spectroscopy, 1988, 131(2): 223-232.

[4] Amiot C, Hafid M, Verges J. BaCl laser-induced fluorescence for seven low-lying electronic states [J].Journal of Molecular Spectroscopy, 1996, 180(1): 121-138.

[5] BergL-E,Gador N, Husain D, et al. Lifetime measurements of the A2Π1/2state of BaCl using laserspectroscopy [J]. Chemical Physics Letters, 1998, 287: 89-93.

[6] Joshua H B, Robert A V, Michael C H, et al. Characterization of the BaCl+(X2Σ+) cation by photoelectron spectroacopy[J]. Journal of Molecular Spectroscopy, 2015, 316:119-121.

[7] Robert A V, Thomas D P, Michael C H, et al. Improved vibrational constants for BaCl+X1Σ+[J]. Journal of Molecular Spectroscopy, 2019, 363:111176.

[8] Yang R, Tang B, Han X Y, et al. Ab initio theory study of laser cooling of barium monohalides[J]. RoyalSociety of Chemistry Advances, 2020, 10(35):20778.

[9] Le Roy R J. LEVEL 8.0: A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasi-bound Levels[CP].Waterloo: University of Waterloo, 2007:663.

[10] Werner H J, Knowles P J, Knizia G, et al. MOLPRO, Version 2012.1[CP].A Package of ab initio Programs, 2012.

[11] Wan M J, Shao J X, Huang D H, et al. Laser cooing of BeCl and BeBr molecules in ab initio method[J]. Phys. Chem. Chem. Phys,2015, 17(40):26731-26739.

[12] Wan M J, Shao J X, Gao Y F, et al. Laser cooing of MgCl and MgBr in theoretical approach[J]. Chem. Phys, 2015, 143(2):024302.

[13] Fu M K, Ma H T, Cao J W, et al. Extensive theoretical study on electronically excited states of calcium monochloride: Molecular laser cooling and production of ultracold chlorine atoms[J]. Chem. Phys, 2016, 144(18): 184302.

[14] 伍冬兰,袁金宏,温玉锋,等.单氯化锶分子低激发态的光谱及跃迁特性[J]. 物理学报, 2019,68(3):033101.

[15] 伍冬兰,谭彬,温玉锋,等. 多参考组态相互作用方法研究MgCl分子低激发态的光谱和分子常数[J].原子与分子物理学报, 2018,35(2):186-192.

SPECTRA AND MOLECULAR CONSTANTS OF THE GROUND AND EXCITED STATES OF BaCl MOLECULES

*WU Dong-lan, Xin Xia, Yuan Jin-hong,Wang Ling-di, MA Rui-hua, LIU San-san,

（School of Mathematic and Physical, Jinggangshan University, Ji’an, Jiangxi 343009, China）

The potential energy curves of the ground and excited states of the BaCl molecule were optimally calculated using the Davidson modified internal contraction multi-reference group interaction (ic-MRCI+Q) method. The potential energy curves were fitted with the LEVEL 8.0 program to obtain the corresponding spectral constants, vibrational energy levels and molecular constants. The data obtained from these computes will be an important reference for future theoretical studies on BaCl molecule.

BaCl molecule; MRCI+Q; spectral and molecular constants; vibrational energy levels

O561.3

10.3669/j.issn.1674-8085.2021.05.001

1674-8085（2021）05-0001-04

2020-08-28；

2021-03-06

国家自然科学基金项目(11564019,11147158)；江西省教育厅科技计划项目(GJJ170654)

*伍冬兰(1978-)，女，江西吉安人，教授，博士，主要从事分子结构与光谱研究(E-mail:wudonglan1216@sina.com)；

辛霞(1999-)，女，山东聊城人，井冈山大学数理学院应用物理学2017级本科生(E-mail:xinxia@jgsu.edu.cn)；

王玲娣(2001-)，女，山东德州人，井冈山大学数理学院物理学2019级本科生(E-mail:wanglingdi@jgsu.edu.cn)；

袁金宏(1977-)，女，江西吉安人，讲师，主要从事理论计算研究(E-mail:yuanjinhong@jgsu.edu.cn)；

马睿华(1999-)，男，河南洛阳人，井冈山大学数理学院应用物理学2017级本科生(E-mail:maruihua@jgsu.edu.cn)；