基于AHP-模糊综合评价法的矿井作业人员作业能力分析*

郭鑫 许开立 陈守坤

(东北大学资源与土木工程学院 沈阳 110000)

0 引言

2009—2018年，我国共发生煤矿生产安全事故约7 107起，死亡人数12 205人，平均每年约发生711起，死亡人数约1 221人[1]。针对我国矿山事故频发的严峻情况，我国学者为此做了深入研究，经过对数据统计分析得出结论：在解决煤矿安全生产的过程中，要降低安全事故发生的可能性，其关键因素是控制人的不安全行为[2]。在非煤矿山事故中，分析各种原因可发现：因违反操作规程或劳动纪律导致的事故起数占事故总量的25%，死亡人数占24%[3]，这是除因生产场所环境不良造成的事故之外占比最多的事故原因，而这2种原因导致的事故约占事故总量的一半以上。

由于矿井作业人员安全评价的随机性和不确定性，使用单一的传统评价方法会导致我们的评价结果被影响从而无法保证客观性。黄广明等[4]将层次分析法与模糊综合评价法相结合，采用定性与定量相结合的模糊综合评价建立金属矿山地压灾害安全风险评价模型。工人自身的安全行为能力不足是导致不安全行为发生的主要原因之一。因此，有效预防和控制矿工不安全行为已迫在眉睫。笔者拟将AHP与模糊理论相结合，构建矿井人员作业能力评价模型，权重由专家组使用AHP来确定，通过模糊综合理论来完成安全评价，运用该模型评价某矿井人员的行为能力等级是否符合其工作要求，开创性地将这种综合评价方法运用到矿井人员的行为能力评价上，希望该方法能为矿井作业人员作业能力评价提供新思路。

1 评价指标体系的建立

对矿井作业人员行为能力进行综合评价是一个较复杂的过程，涉及到的内容较多，考虑的因素也较广，因此建立科学、合理的安全评价指标体系是对矿井作业人员行为能力进行安全评价的关键。本文建立了以意识水平、安全能力、基本素质、业务能力、外界因素为一级指标，责任意识、理解能力、生理素质、工作年限、企业安全文化等20个影响因素为二级指标的评价体系，如表1所示。

2 基于层次分析法确定指标权重

2.1 层次分析法基本原理

AHP是对定性问题进行定量分析的一种灵活简便又实用的多准则决策方法。它擅长把复杂问题中的各种指标因素划分得层次有序，以两两比较的方式对一定客观现实进行主观判断，从而将专家意见和分析者的客观判断巧妙地结合起来[5-6]。

2.2 层次分析法的基本步骤

(1)构造判断矩阵

请专家根据1～9比例标度法分别对各个指标层次指标因素进行重要程度的判断打分，分数越高代表其相对重要程度越高，数字的取值所代表意义见表2。

表2 标度法的含义

通过专家打分得到两两比较判断矩阵，考查B层因素和A层因素的相对重要性，可以得出A、B判断矩阵。

(2)一致性检验[7]

建立判断矩阵后，求出判断矩阵的最大特征值和相应的特征向量，进而对判断矩阵进行一致性检验。通过下式计算一致性指数(CI)：

(1)

(2)

式中，A为A-B判断矩阵；n为判断矩阵阶数；wi向量是之前进行矩阵运算时的列向量；λmax为判断矩阵最大特征值。

两两之间比较的一致性是采用一致性比率来计算，其计算公式为

(3)

式中，RI为随机一致性指标，随判断矩阵阶数n的变化而变化，其取值见表3。

表3 RI随机一致性的取值

3 模糊综合评价法确定安全等级

(1)确定系统危险性评价指标特征值矩阵[8-9]

设X为n个系统样本构成的集合，每个样本有m个评价指标，则有系统危险性评价指标特征值矩阵，即

(4)

式中，Xij为样本j指标i的特征值；i=1，2，…，m；j=1，2，…，n。

(2)确定指标标准矩阵

m项指标按c级危险标准评价，则指标标准矩阵为

(5)

式中，wih指标代表指标i的h级标准值；h=1，2，…，c。

(3)利用三角形隶属函数模型确定隶属度[10-12]

此种模型是根据某一指标特征值的危险性等级最多仅与相邻的2个等级有关的原则提出的。危险性等级愈小，人员安全能力越好，即：

(6)

式中，μ(x)为x对U的隶属度。

(4)一级综合评价

第i类因素的模糊综合评价集合为

Ci=wi×Ri

(7)

式中，Ci为相对于Bn层的综合模糊运算结果；wi为各因素相对于Bn层的权重；Ri为模糊评价矩阵。

(5)进行多层次综合评价

同理，按照步骤(4)进行，可最终求出目标层的模糊综合评价矩阵，根据最大隶属原则，确定评价对象所属的评价等级，给出评价结论。

4 案例应用与分析

4.1 权重计算

针对以上5个一级指标因素以及20个二级指标因素进行各个层次的重要度两两比较，并邀请5位不同级别的领域专家进行重要度确认，运用Yaahp软件进行指标权重的计算。

依照上述方法可以依次计算出第二层次的权重集与CR值并利用软件Yaahp软件对其进行一致性检验。其权重值和一致性检验结果见表4—表9。

通过表4—表9中数值的计算分析可以得出各个矩阵均符合要求，通过了一致性标准的检验，因此验证了所得权重分配的权重值的可靠性，可以进行下一步研究。

表4 判断矩阵A-B数值

表5 B1判断矩阵数值

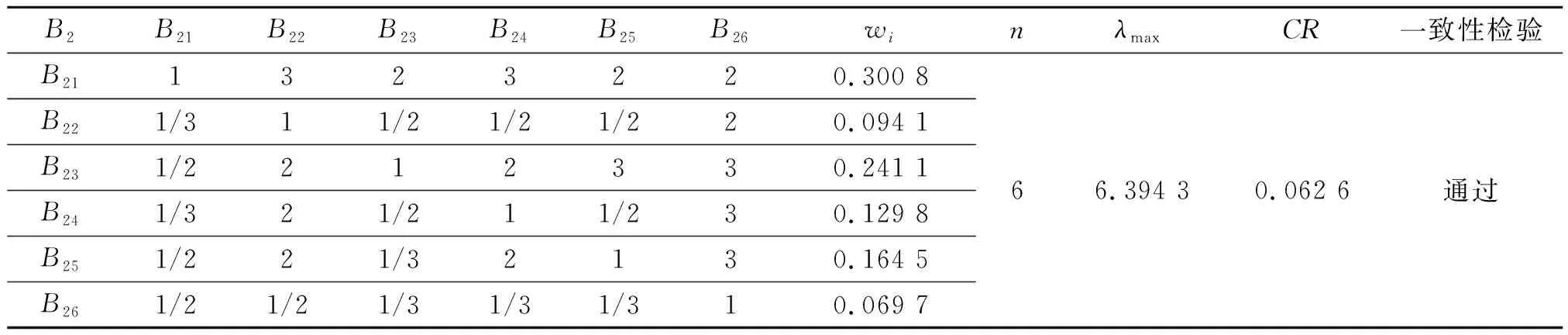
表6 B2判断矩阵数值

表7 B3判断矩阵数值

表8 B4判断矩阵数值

表9 B5判断矩阵数值

4.2 安全能力等级划分

(1)划分评价等级

本文将矿井作业人员作业能力划分为5个等级，具体分数等级标准见表10。

表10 评价等级划分

(2)确定专家打分权重

接下来以工人甲为例进行计算。首先，请5位专家分别打分，根据表10中各等级所对应的分数范围，可以取各分数范围的中间值作为指标标准矩阵每一行的元素，因矿井作业人员行为能力评价指标体系中各指标均为定性指标，所以指标标准矩阵Ω中每一行的元素都一样，均为9，7，5，3，1。根据公式(6)，可算出各指标的隶属度，如表11所示。

B级综合评价

查阅表5可知：B1层下级各个指标(即B11、B12、B13)相对于下层的权重分别为0.332 5、0.527 8、0.139 6，即：

w1=[0.332 5，0.527 8，0.139 6]。

通过公式计算可知模糊综合评价矩阵：

根据式(7)可得指标B1的评价结果：

B1=w1×R1=[0.507 5，0.392 6，0.099 8，0，0]

重复以上步骤，可得到指标层、目标层的结果。

表11 最后一级各指标特征值以及隶属度

确定A级评价等级

查阅表4可知：A层下级各个指标(即B1、B2、B3、B4、B5)相对于A层的权重分别为0.224 7、0.473 8、0.148 4、0.103 3、0.049 8，即：

wa=[0.224 7，0.473 8，0.148 4，0.103 3，0.049 8]。

查B级综合预算结果可知模糊综合评价矩阵：

根据公式(7)可得指标A的评价结果：

A=wa×Ra=[0.216 1，0.579 8，0.167 3，0.034 7，0.002 1]

根据其评价结果可以知道其总分：

查阅表10可知，该名工人行为作业能力等级为Ⅱ级，适合危险程度和操作难度较高的岗位。

5 结论

(1)建立了矿井作业人员行为能力综合安全评价的指标体系，该指标体系包括5个二级指标和20个三级指标。采用层次分析法确定了矿井作业人员行为能力综合安全评价的指标体系中各个指标的权重。

(2)建立了矿井作业行为能力综合安全评价的模糊数学模型。用模糊综合评价数学模型法进行等级评定，最终给出评价矿井作业工人作业能力水平的方法，根据对作业人员作业能力评价的结果，可判断有关人员是否满足安全作业的要求，从而为优选矿井作业人员提供评判依据。