基于解析法和数值法反演哈尔滨漫滩区水文地质参数*
2021-11-19姚德华党峰荣
李 磊 陈 干 唐 沛 姚德华 党峰荣
(1.中铁第五勘察设计院集团有限公司,102627,北京;2.南京大学地球科学与工程学院,210023,南京∥第一作者,高级工程师)
渗透系数是基坑疏降水、地下水渗流控制、地质环境影响评价等水文地质计算中的关键参数[1-2]之一。获取水文地质参数的方法很多,如:直接采用《水文地质手册》[3]及GB 50287—1999《水利水电工程地质勘察规范》[4]中罗列的经验值;通过室内试验进行测定[3];通过现场抽水试验或注水试验,根据抽、注水量和监测水位的动态关系,通过解析公式或数值法进行反演计算[5]。文献[3-4]中给定的不同岩性的经验参数往往是一个取值范围;室内试验测定的参数应用到场地工程存在尺度效应问题;而解析法引入了大量的假设条件,如含水层几何形状规则、均质各向同性、边界条件单一等,其使用条件苛刻,难以满足实际复杂水文地质条件下参数反演的要求。采用上述方法求解得到的水文地质参数结果存在一定偏差,难以满足工程计算的要求[6]。因此,有必要采用解析法与数值法相结合的方法进行含水层水文地质参数的反演[7-9]。通过对多种方法反演的水文地质参数进行对比,相互验证水文地质参数的合理性,以降低单种方法求解水文地质参数的不确定性。这对于水文地质条件的正确判别,以及地下水控制方案的合理制定具有重要的工程应用意义。
哈尔滨地铁4号线一期第1标段全段位于松花江以北、阿什河以南的漫滩区,漫滩区含水层厚度较大。以往诸多地下水控制工程,如基坑降水、地铁抗浮等工程,更多地凭借工程人员的经验进行设计,造成了大量的工程地质问题[10-12]。因此,本文分别采用解析法和数值法[8]求解研究区段主要含水层的水文地质参数,如渗透系数K、导数系数T等,对哈尔滨漫滩区地铁工程地下水渗控具有借鉴意义。
1 科技五街站抽水试验工程概况
1.1 抽水试验场地条件
抽水试验场地位于哈尔滨市松北区地铁4号线科技五街站附近。抽水试验井采用“5抽+3观测”的组合。其中,5口抽水井沿东西向直线布置,间距均为10 m;3口观测井与抽水井连线垂直布置,观测井1(观1)与抽水井3(主井3)间距为10 m,与观测井2(观2)间距为20 m,与观测井3(观3)间距为30 m。抽水试验井位置详见图1。单井抽水试验设计参数见表1。

图1 科技五街站抽水试验井布置图Fig.1 Location of pumping test wells around Kejiwujie Station

表1 抽水试验场地单井抽水试验设计参数表Tab.1 Design parameters table of single well pumping test Station
科技五街站抽水试验井揭示,研究区段的地层主要为厚45~55 m的第四系松散堆积物,为现代河漫滩相堆积,分布较为广泛。抽水试验场地自上而下主要为:地表上覆2.0~6.0 m的亚黏土或亚砂土,低洼处为淤泥质黏土;全新统下段细砂、中粗砂;下更新统为中粗砂、砂卵砾石层;下覆白垩系嫩江组泥岩、砂岩及泥质砂岩,构成了松散堆积物底板。
研究区段含水层为典型的非均质微承压含水层,地下水主要补给来源于大气降水的渗入补给、丰水期松花江江水侧向渗入补给,以及地下水的侧向径流补给;地下水的排泄主要以蒸发为主,其次为地下水侧向径流排泄,枯水期排泄方式为向松花江排泄和人工开采。地下水位埋深仅为2.0~4.5 m,年变幅一般为1.0~3.0 m。
1.2 抽水试验数据分析
本次抽水试验分单井抽水试验和群井抽水试验两种类型。采用单井抽水试验分别进行3次不同水位降深S的抽水。其中,最大水位降深发生在采用最大抽降能力抽水时,其余2次水位降深分别为最大水位降深值的1/3和2/3。3次抽水落程采用的抽水流量Q分别为221.1 m3/h、154.0 m3/h和78.5 m3/h。
群井抽水试验中,5口抽水井的抽水流量全部采用200 m3/h,并对其进行一次水位降深的抽水,同时读取各观测井水位。现场均采用稳定流进行抽水,为了满足非稳定流的计算要求,结合非稳定流要求进行数据观测。单井和群井抽水试验结果如图2~3所示。
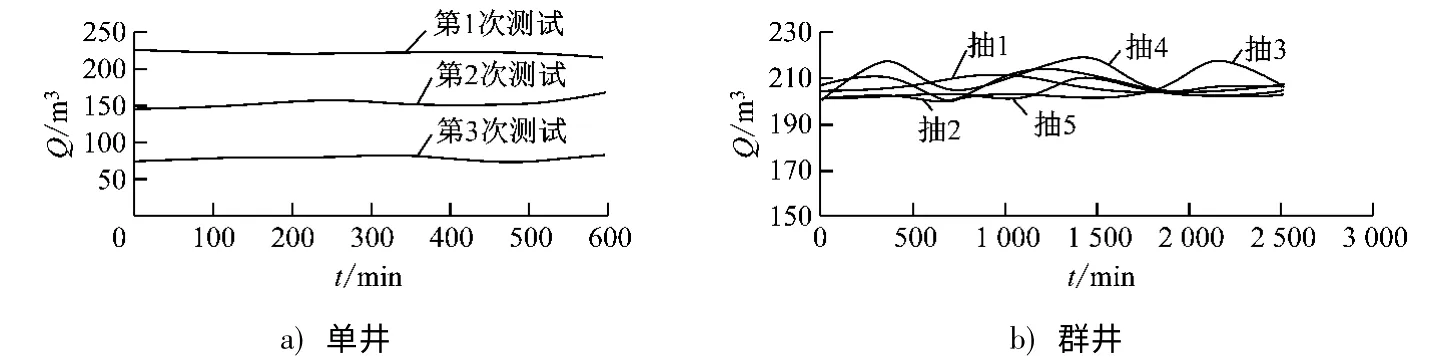
图2 单井和群井抽水试验Q-t关系图Fig.2 Q-t relationship between single well and group well pumping tests
2 采用解析法求解抽水试验场地水文地质参数
2.1 计算方法
本次非稳定流水文地质参数的计算,分别选取稳定流Dupuit计算公式、非稳定流Theis计算公式和水位恢复法反演水文地质参数[3]。
2.1.1 稳定流Dupuit计算公式
抽水试验采用完整井进行抽水。场地含水层近似水平、均质、各向同性,等水头面是共轴的圆柱面,和过水断面一致。抽水井附近达到稳定或近似稳定后,可采用Dupuit公式进行计算。

图3 单井和群井抽水试验S-t关系图Fig.3 S-t relationship between single well and group well pumping tests

式中:
K——渗透系数,m/d;
H——微承压含水层厚度,m;
Q——抽水井出水量,m3/d;
S1——1号观测井的水位降深,m;
S2——2号观测井的水位降深,m;
r1——1号观测井与抽水井的距离,m;
r2——2号观测井与抽水井的距离,m。
2.1.2 非稳定流Theis计算公式和水位恢复法
利用群孔(完整井)在抽水试验场地进行定流量非稳定流抽水试验。试验中,微承压含水层近似均质、等厚、侧向无限延伸,含水层中水头损失符合达西定律。采用Theis计算公式进行抽水时段水文地质参数估算;或利用抽水恢复阶段的观测资料,采用水位恢复法进行水文地质参数计算。
2.1.2.1 非稳定流Theis计算公式
非稳定流Theis计算公式如下:

式中:
W(u)——泰斯井函数,u=r2/(4 at);
S (r,t)——距离抽水井r处,t时刻的水位降深值,m;
a——压力系数,m2/d;
T——导水系数,m2/d;
t——抽水延续时间,s。
2.1.2.2 水位恢复法
水位恢复法的计算公式如下:

令:

则式(3)变为:

式中:
h——井内恢复水位高度,m;
ha——抽水稳定时井内水位高度,m;
R——影响半径,m;
r——抽水井半径,m。
停抽稳定后,与t1、t2相应的h1、h2分别为:

求解式(5)—式(6),得到:


2.2 计算结果分析
基于不同水位降深的单井抽水试验和群孔非稳定流抽水试验数据,通过Aquifer test软件,采用稳定流Dupuit计算公式、非稳定流Theis计算公式和水位恢复法分别反演水文地质参数,计算结果如表2所示。非稳定流Theis函数配线见图4。通过不同解析法求得的渗透系数为35.9~71.3 m/d,导水系数为1.61×103~3.21×103m2/d。

表2 各解析法下抽水试验场地水文地质参数统计表Tab.2 Statistical table of hydrogeological parameters of pumping test sites
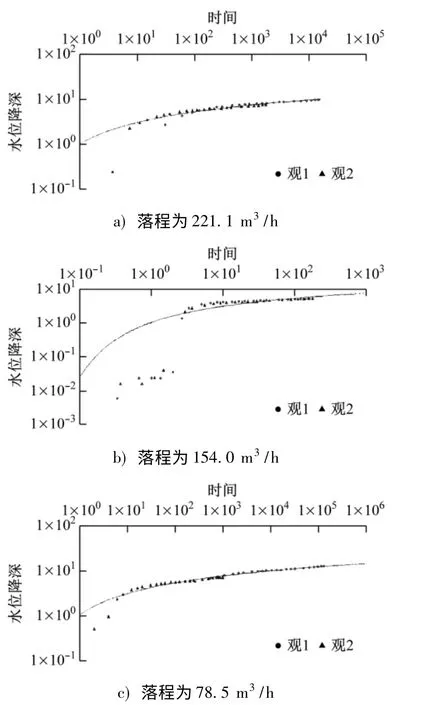
图4 非稳定流Theis函数配线图Fig.4 Distribution diagram of unsteady flow Theis function wirings
3 采用数值法求解抽水试验场地水文地质参数
为了更加准确地刻画抽水试验场地的水文地质特征,本文利用FEFLOW软件进行三维地下水流建模,并采用抽水试验动态数据对模型进行识别,通过反演得到该场地最佳的水文地质参数。
3.1 抽水试验场地地下水流概念模型
根据抽水试验场地的水文地质条件,对含水层结构进行概化。地下水流概念模型的地层由上到下划分为3层:
1)第四系覆盖层(素填土、粉土、粉质黏土层)厚3.0 m;
2)第四系孔隙微承压层厚39.0 m;
3)基岩隔水底层厚6.8 m。
由于研究区段范围较小,且模拟区主要含水层的岩性变化较小,因此将含水层概化为均质、各向异性的介质。
为减少边界选取的随意性给计算结果带来误差,通过解析法试算抽水试验的影响半径。以抽水井(主井1—主井5)为中心,向四周长、宽方向各延伸1 400 m的区域为模拟区。排除抽水井对边界的影响,模拟区范围为2 853 m×2 853 m。
该模型共分为3层。其中,上边界为粉质黏土层,为自由面,由于不考虑大气降水入渗、蒸发排泄等因素,故上边界不作处理,默认为隔水边界;下边界为基岩底板,将其设置为隔水边界;模拟区周界未受到抽水影响;将侧向模拟边界设为定水头补给边界;给定水头值为现场实测的含水层初始水位111.22 m。
3.2 抽水试验场地地下水流数学模型
根据上述建立的概念模型,在不考虑水的密度变化的前提下,将该模型概化为三维微承压含水层中的非稳定流数学模型:

式中:
Ω——渗流区域;
h——含水层的水位标高;
Kx、Ky、Kz——分别为x、y、z方向的渗透系数;
μ——含水层的给水度或者贮水系数;
ε——含水层的源汇项;
h0——含水层的初始水位分布;
Γ——渗流区域的给定流量边界,包括渗流区域的侧向流量或隔水边界和含水层底部的隔水边界;
Kn——边界面法向方向的渗透系数;
q(x,y,z,t)——定义为给定流量边界的单位面积流量,本次为隔水边界,设为0。
3.3 抽水试验场地地下水流数值模型
图5所示为抽水试验场地三维数值模型图。该模型在竖向分为3层,在横向采用三角形网格剖分(抽水井和观测井附近网格需加密),最小的网格面积为0.04 km2,每层共剖分为11 438个网格,形成5 852个节点。

图5 抽水试验场地三维地下水流数值模型图Fig.5 Schematic diagram of 3D ground water flow numerical model at pumping test spots
非主要含水层初始渗透系数和贮水系数等参数的取值主要根据含水层岩性,并结合《水文地质手册》进行查取,而主要含水层的初始参数则通过解析法进行求取(见表2)。本次模拟区岩性分布均匀,故在横向上不再对其进行参数分区。
3.4 水文地质参数模拟反演结果分析
选用群孔抽水试验时段为模拟期,对孔隙含水层水文地质参数进行反演,其中,时间步长通过误差迭代自行控制。在参数反演中,依据观测井水文观测值和计算水位的差值来调整渗透系数。通过反复调试,得到该参数的最佳拟合效果,如图6所示。通过数值法反演所得的含水层渗透系数为44.5 m/d。

图6 基于数值法的地下水水位拟合曲线和流场图Fig.6 Groundwater level fitting curves and flow field diagram based on numerical method
通过构建数值模型,可模拟在不同抽水时刻试验区地下水流动态。如在抽水开始后1 800 min,各抽水主孔产生的漏斗已相互叠加,在观测孔处模拟水位与观测水位误差为0.1~0.2 m,精确地反映了群井抽水过程中地下水位的动态变化。
本次采用解析法求解得到的渗透系数为35.9~71.3 m/d,平均值为54.1 m/d;采用数值法反演得到的渗透系数为44.5 m/d。考虑在实际工程中,解析法对工程条件进行了假设和简化,且拟合的随意性较大,而数值法能更精确地描述含水层的实际结构和地下水的真实运动状态。
4 结语
1)利用解析法计算得到孔隙微承压含水层渗透系数为35.9~71.3 m/d,平均值为54.1 m/d。
2)数值法模拟了群孔非稳定流抽水试验过程中地下水流动态过程,通过拟合得到主要含水层的渗透系数为44.5 m/d。
3)解析法和数值法计算结果的相互验证,大大增加了水文地质参数反演结果的可靠度,可为后期地铁工程地下水渗控方案的制定和实施提供参数。
