关于高速铁路动车组牵引电机故障预测的研究
2021-11-19荆玉山
荆玉山
(中国国家铁路集团有限公司 北京 100055)
0 引言
牵引电机是高速铁路动车组走行部的直接动力来源,目前,对于牵引电机运行状态的掌握主要依靠安装于定子铁芯和两端轴承的温度传感器发送的实时数据,但对其应用则以实时跟踪为主,更偏向于事后分析,无法在故障发生之前预知或提示。国内对牵引电机的故障预测方法的研究中,赵硕丰[1]等人通过对牵引电机的输入输出电流值的监控,建立一种基于谐波分析的牵引电机预测模型。牛齐明[2]等人通过提取牵引电机的振动特性,拟合了牵引电机正常情况下的标准振动数据,通过标准振动数据与运行数据的比对,达到预测牵引电机故障的目的。然而根据本文的调查研究发现,这些预测模型所需要的数据,在高速铁路动车组中并没有监控设备可以进行实时传输,只能在线下对动车组牵引控制单元进行数据下载得到。在动车组运营单位中,针对动车组某一部件的数据下载,有一定的作业时间及作业周期,因此很难通过这些数据对动车组进行相对实时的信息诊断及故障预测。本文基于动车组WTDS传输的实时牵引电机温度数据,建立了一个牵引电机故障预测模型,满足一定预测精度的同时,也可以保证应用方面的时效性。
1 动车组牵引电机故障预测模型的建立
目前,多元线性回归算法[3-7]被广泛用于各行各业的预测计算。本文结合动车组实际情况,采用多元线性回归算法建立牵引电机故障预测模型。相较于电流、电压、振动幅值、振动频率等数据,牵引电机的温度数据更容易得到且可以通过温度传感器传输到WTDS与地面进行实时传输。通过动车组运营单位的调查研究发现,牵引电机的异常状态完全可以通过运行时的温度特征体现,因此可以将牵引电机运行时的峰值温度作为研判牵引电机故障的依据。下文以牵引电机温度峰值作为预测的目标函数,考虑到牵引电机温度传感器或者网络故障引起的牵引电机温度突变会对函数的拟合结果造成精度缺失,进行预测前需对车载数据进行数据清洗。
对于传输的n个运行温度数据tn,设定筛选变量ε。如果:
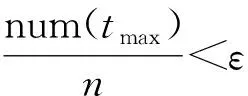
(1)
则对于采集的牵引电机温度数据tmax进行剔除,对剔除后的n-1个运行数据进行重新清洗,将满足条件的tmax作为牵引电机温度峰值。
对于剔除清洗后的n组预测目标数据yn及其k个影响因子xk:
(2)
其中:β1为回归系数,μ1为随机扰动项。通过对动车组牵引电机温度数据的研究发现,动车组在不同运行线路、不同的检修条件下,牵引电机的温度峰值有着显著的不同。分析认为:运行中牵引电机温度的峰值变化,是一个连续的、相互影响的过程,因此可以由前日牵引电机的运行状态,结合当日的运行实际对当日牵引电机的温度峰值进行表征。由于牵引电机采用强迫式风冷散热,无散热格栅,结构相对封闭,故外界温度及天气状况因素对牵引电机峰值温度的影响微乎其微。因此,此处将牵引电机检修项目信息、运行线路状况、行车信息及前一天牵引电机运行状态作为牵引电机温度峰值预测的影响因子,可以得到较为精准的预测结果。
为保证拟合的回归方程可以得到良好的精度,根据残差的平方和最小原则,有:
(3)

为防止数据中存的离群值xout(对应的残差具有较大方差的值)降低预测精度,需对离群值xout进行剔除处理。对于n组牵引电机温度数据yn,使用奈尔检验法检验离群值,则有:
(5)
(6)
(7)
对数据进行清洗后,则预测值yn+1可以表达为:
(8)
2 牵引电机温度峰值预测结果
选取一组CRH5A型动车组,对其牵引电机温度数据进行了长期的数据跟踪,使用牵引电机故障预测模型,对牵引电机的状态参数进行预测分析。以7月1日的牵引电机温度峰值作为预测模型的初始迭代值。将初始迭代步的预测值设置为零,其后的温度峰值数据作为算法的训练集。设定筛选度量ε=0.003 5,对温度传感器传输的温度数据进行筛选,对清洗后的数据进行预测分析,结果如图1所示。
观测图1中动车组的牵引电机预测结果可知,7月1日至7月20日的牵引电机温度峰值预测结果均与实际值有较大的差距,这是由于在初始训练阶段,影响因子的系数βk的个数k大于回归方程的个数n,在回归分析中,影响因子的系数βk存在空值,因此对于牵引电子的预测结果yn+1呈现着跳动的不稳定性。随着数据的不断积累,可用于回归的方程数目不断增加,影响因子的系数βk的空值渐渐消除,预测值也逐渐向真实值靠拢。由图1可知,在经过25天的数据训练之后,对于CRH5A型动车组牵引电机的峰值温度预测精度可达92.3%。

图1 多元线性回归算法的CRH5A型动车组牵引电机预测结果
3 预测模型的改进
由图1可知,采用多元线性回归算法的预测模型精度可以达到92.3%,但实际生产应用中,8.7%的误差并不在一个可接受的范围内。多元线性回归模型默认各影响因子与预测结果间存在着线性关系,然而生产实际中,简单的线性关系并不能完全表达两者间存在的联系,这就导致了预测值与真实值间存在较大的误差。本文采用多元非线性回归算法[8-9]对牵引电机的预测模型进行改进。
在对传感器传输的牵引电机温度数据进行数据剔除和清洗后,对于采集的组牵引电机温度数据及牵引电机温度峰值的各影响因子的数据,构建多元非线性回归方程:
(9)
对于多元非线性回归方程,根据残差的平方和最小原则,有:
(10)
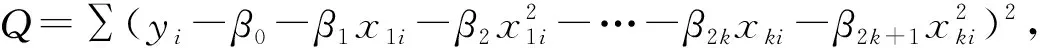
(11)
并使用奈尔检验法剔除检验离群值xout后,则预测值yn可以表达为:
(12)
4 多元非线性回归算法的牵引电机温度峰值预测结果
本文采用多元非线性回归算法对上述CRH5A型动车组牵引电机温度数据进行预测分析,以7月1日的牵引电机温度峰值作为预测模型的初始迭代值。设置初始迭代步的预测值为0,设定筛选变量ε=0.003 5,多元非线性回归算法与多元线性回归算法的预测结果如图2所示。
观测图2中动车组的牵引电机预测结果可知,多元非线性回归算法的收敛周期远远大于多元线性回归算法,经过43天的数据培养后才逐渐收敛于真实值。这是由于多元非线性回归算法中,虽然未知数的数量与多元线性回归算法一致,但其影响因子的二次方项同样需要一定数量的方程进行回归。在积累到一定数量的数据之后,多元非线性回归算法也逐渐向真实值靠拢,但其收敛程度远远优于多元线性回归算法,其对于CRH5A型动车组牵引电机的峰值温度预测精度最终可达95.2%。
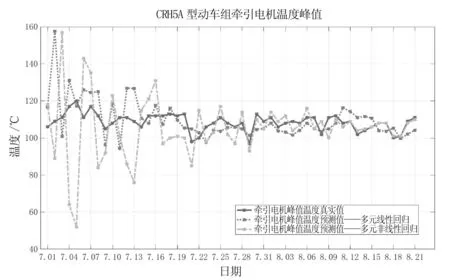
图2 多元非线性回归算法的CRH5A型动车组牵引电机预测结果
5 结论
针对目前牵引电机故障预测模型中数据采集困难、实时传输不易的问题,提出了一种基于牵引电机温度的故障预测模型。主要结论如下:
(1)通过多元线性回归算法建立了牵引电机峰值温度预测模型,该模型基于温度传感器采集的数据,可以满足实时传输的需求。将牵引电机检修项目信息、运行线路状况、行车信息及前一天牵引电机运行状态作为牵引电机温度峰值预测的影响因子,预测精度可达92.3%。
(2)针对多元线性回归算法精度难以满足实际生产需求的问题,使用多元非线性回归算法对预测模型进行了改进。改进后的预测模型收敛周期增加,但最终可达到的预测精度有了大幅提升。多元非线性回归算法的牵引电机峰值温度预测精度可达95.2%。
