基于加权多新息AEKF的锂电池SOC在线估算
2021-11-19乔家璐王顺利于春梅史卫豪
乔家璐,王顺利,于春梅,史卫豪,杨 潇
(西南科技大学信息工程学院,四川绵阳 621010)
在汽车工业的发展过程中,纯电动汽车以其低噪音、低污染、结构简单、维修方便等优点逐渐成为新能源汽车发展的主要方向[1-2],锂离子电池以其能量密度大、重量轻、无记忆效应、充放电电压稳定等优点成为电动汽车电源的最佳选择[3-4]。随着锂电池的应用范围不断扩大,电池状态监测和安全问题成为了亟待解决的难题[5]。作为车辆系统和电池管理系统的一个重要参数,电池荷电状态(state-ofcharge,SOC)的精确在线实时估计不仅可以保护电池[6],防止过充电和过放电现象的发生[7-9],延长其使用寿命[10],还可以为用户提供更直观的续航里程和更好的驾驶体验,因此研究准确高效的SOC估算方法具有重要意义[11-13]。
常用的SOC 估计算法有直接测量法、数据驱动法和基于模型的方法[14-15]。直接测量通常包括开路电压法和安时积分法[16]。数据驱动是在机器学习和人工智能算法的基础上发展起来的,它需要大量的数据和高昂的计算成本[17]。基于模型的方法通过建立等效电路模型来模拟锂离子电池内部的动态反应过程[18],并结合控制理论中的滤波算法对SOC进行估计,常用的有扩展卡尔曼滤波(extended Kalman filtering,EKF)算法[19-20]。但锂电池内部结构复杂,呈强烈非线性,传统算法难以实现SOC的高精度估计[21]。经过该领域诸多学者的不断开拓与创新,提出一种扩展卡尔曼滤波与自适应无迹卡尔曼滤波相结合(extended Kalman filtering-adaptive unscented Kalman filtering,EKF-AUKF)的算法来估算SOC,获得了较高的精度[22]。提出了一种AUKFBP 网络的估算方法,避免了UKF 过于依赖电池模型的精度和BP 神经网络收敛速度慢的缺点,又保留了UKF鲁棒性高和BP神经网络非线性特性强的优点[23]。但UT 变换中Cholesky 分解矩阵的半正定性无法保证,极有可能导致滤波器精度降低、甚至发散,不适合实际应用。
为了更精准表征电池的动态特性和进行电池状态的估算,本文提出一种加权多新息自适应扩展卡尔曼滤波(multiple weighted-adaptive extended Kalman filtering,MW-AEKF)方法对电池SOC 进行估计,引入了二阶RC 等效电路模型,采用带遗忘因子的递推最小二乘法(forgetting factor-recursive least square,FFRLS)在线辨识电池参数。为验证算法可行性,在自定义动态测试应力(dynamic stress test,DST)工况和北京公交动态测试(Beijing bus dynamic stress test,BBDST)工况下分别进行实验验证并与其他算法进行对比。
1 理论分析
1.1 二阶RC等效电路建模
综合考虑建模的精准性和计算的简便性,采用二阶RC等效电路模型,如图1所示。

图1 二阶RC等效电路模型Fig.1 Second-order RC equivalent circuit model
在图1中,UOC表示开路电压;UL表示端电压;R0表示欧姆内阻。其中R1和R2分别表示电化学极化电阻和浓差极化电阻,C1和C2分别表示电化学极化电容和浓差极化电容,其电压和电流的表达式如式(1)所示。
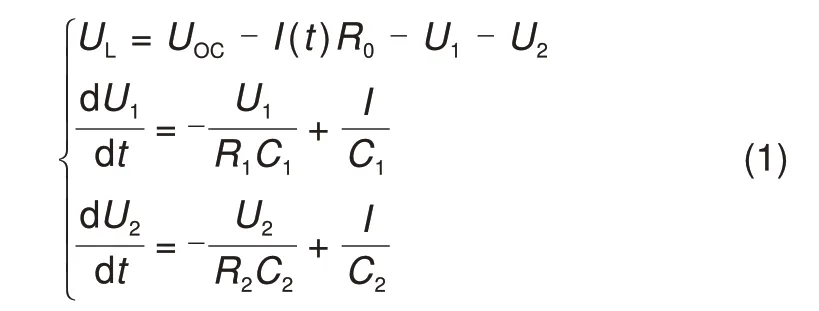
选择[SOCU1U2]T作为状态变量,对等效电路进行离散化处理,得到其离散状态的状态空间表达式如式(2)所示。
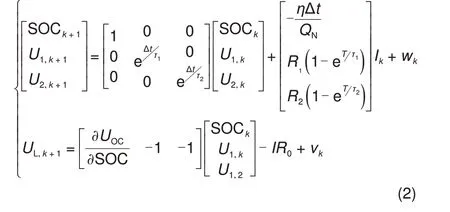
式中,∆t为采样时间间隔;T为时间常数,T1=R1C1,τ2=R2C2;wk为状态误差,vk为测量误差,分别是协方差矩阵Q和R的零均值白噪声;QN为电池的额定容量;η为库仑效率,设为0.98。
1.2 基于FFRLS的在线参数辨识
递推最小二乘法(recursive least square,RLS)通过对系统参数的不断修正和更新,能够准确捕捉系统的实时特性,待辨识模型的离散方程和相应的差分方程如式(3)所示
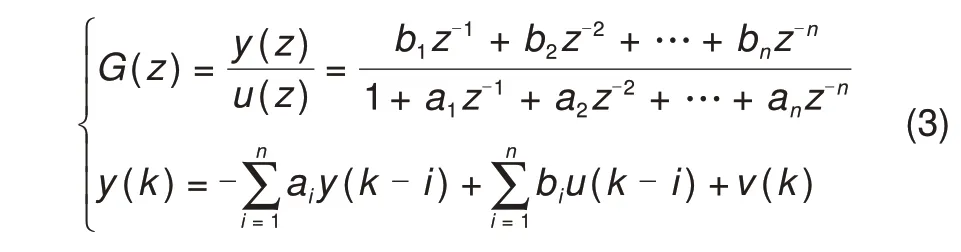
式中,ai和bi是系统待辨识参数向量;y(k)为系统输出的k时刻的观测值;U(k)为k时刻的系统输入;v(k)为平均值为0的随机噪声。
为了提高RLS算法的在线辨识能力,在原有算法中增加了遗忘因子λ,称为FFRLS算法。遗忘因子的作用是根据不同时刻数据包含的信息量来对其进行最合理的分配和利用。引入遗忘因子λ(0<λ<1)后,改进的递推方程如式(4)所示。


设时间常数τ1=R1C1,τ2=R2C2,a=τ1τ2,b=τ1+τ2,c=R0+R1+R2,d=R1τ2+R2τ1+R0(τ1+τ2)。将s=[x(k)-x(k-1)]/T代入式(5)进行离散化,式中T为采样时间,设定为0.1 s,将式(5)离散化后为了方便参数辨识,将k1~k5代替实际参数进行抽象化表达,如式(6)所示。
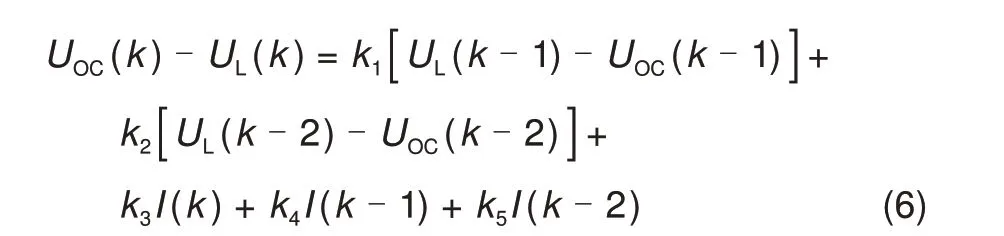
式中,待辨识的参数向量为θ=(k1,k2,k3,k4,k5)T。在线参数辨识完成后,实际电池参数通过式(7)获得。

1.3 加权多新息计算
为了提高EKF在非线性系统中的适应性,通过利用多个时刻数据信息的方式将算法中的残差标量扩展为新息矩阵,建立了基于新息的辨识理论和方法。
基于多新息理论,将新息e(k)=UL(k)−Ckx(k|k−1)扩展到新息矩阵E(p,k),如式(8)第1部分所示。为了进一步提高估算精度且适应计算的兼容性,将扩展卡尔曼滤波增益K(k)扩展为滤波增益矩阵K(p,k),如式(8)第2部分所示。

将新息矩阵E(p,k)和滤波增益矩阵K(p,k)引入标准EKF 算法后,状态更新方程如式(9)所示。其中p为时间步长,表示k时刻状态的估算需要利用p个时刻的新息值与滤波增益值。
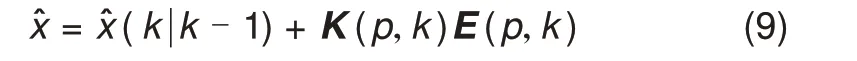
一般认为,由于矩阵中不同时刻的新息e(k)的所处时刻不同,其中包含的信息量也不同,为不同时刻的新息配置不同的权重因子,如式(10)所示
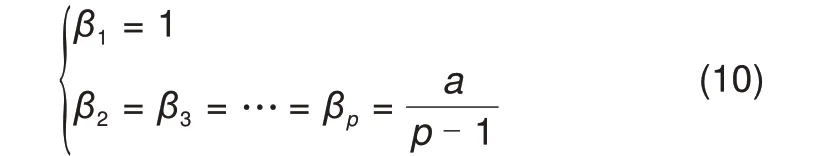
式中,p为新息数据宽度,即时间步长;a为权重的配置系数,其值设为1.98。完成配置后的加权多新息矩阵和状态更新方程如式(11)所示
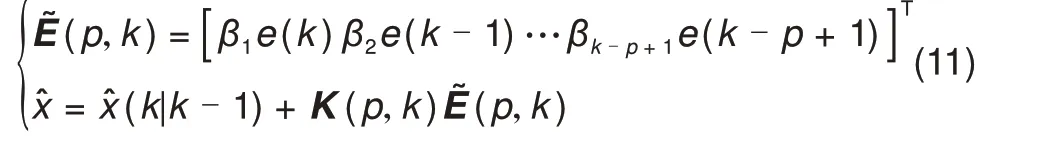
综上所述,EKF中加权多新息的计算原理和具体实现流程如图2所示

图2 加权多新息计算Fig.2 principle of multiple weighted calculation
1.4 加权多新息AEKF
采用AEKF算法的本质是通过测量过程中的误差协方差来调整SOC 的当前值以实现更精确的估算。首先,对系统进行初始化,设定初始状态的估计值x0和误差协方差矩阵P0如式(12)所示

然后,根据k−1时刻的状态和误差协方差矩阵来对k时刻的状态和误差协方差矩阵进行更新,计算过程如式(13)所示
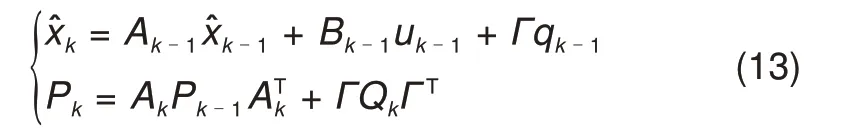

式中,C为系统观测矩阵,Rk为测量噪声vk的方差。测量数据用于对下一时刻状态估计和误差协方差进行持续更新,表达式如式(15)所示
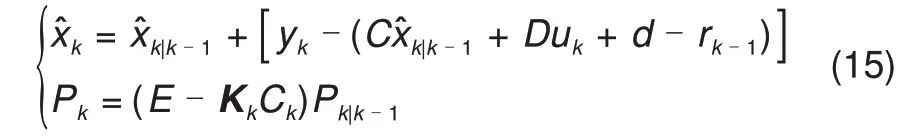
式中,D为驱动预测系统观测量,rk为测量噪声vk的均值,E为单位矩阵。最后,利用测量数据对噪声的均值和方差进行在线估计,从而实现对系统噪声和过程噪声的均值和误差协方差的迭代更新和对SOC 估计的自适应调节,计算方程如式(16)所示
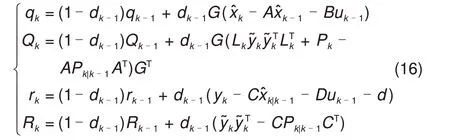
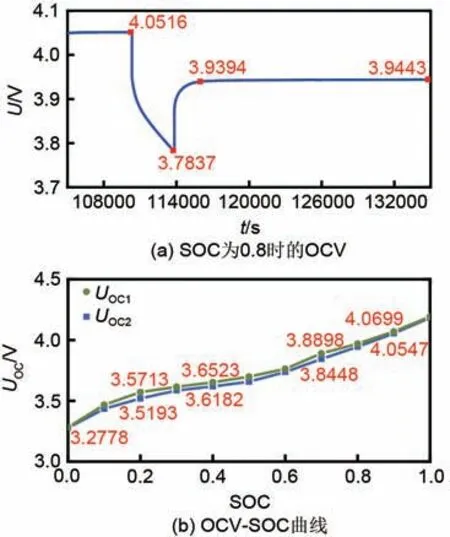
式中,G=(ΓTΓ)ΓT,dk−1=(1−b)/(1−bk)。b为遗忘因子且0 图3 加权多新息AEKF估算SOC总体流程Fig.3 Total process of MW-AEKF SOC estimation 为了验证本文所提出算法的运行效果,在DST、BBDST 这些不同的复杂工况下进行了实验验证,并与其他算法进行对比验证。 实验选取德力普电池科技有限公司生产的额定容量为50 A·h的锂离子铝壳电池,深圳亚科源科技有限公司提供的BTS200-100-104电池测试设备作为实验平台。实验中使用的锂离子电池如图4(a)所示,能够进行充放电并实时监测和记录电流、电压状态的电池测试设备如图4(b)所示。 图4 实验设备Fig.4 Experimental equipment 通过实验可以得到OCV-SOC曲线,实验过程为:将电池充满电,然后恒流放电至特定的SOC值,静置一定时间后等待电池达到稳定状态。此时,测量与该SOC值相对应的OCV值。重复该过程,将电池每次以额定电量的10%依次进行放电,直至电池放电到0 SOC,以获得放电OCV-SOC曲线。由图5(a)可知,SOC 为0.8 时,OCV 为3.9443 V。考虑到电池的迟滞效应,将电池以同样的方式进行充电实验。一般情况下,充放电的OCV-SOC 曲线并不完全一致,而是会形成一段两端有间隙的带状迟滞结构,如图5(b)所示。UOC,1代表充电过程曲线,UOC,2代表放电过程曲线,通过取平均的方式得到更加准确的OCV。 图5 电池OCV的迟滞效应曲线Fig.5 Hysteresis characteristic curve of battery OCV 采用HPPC 工况下获取的实验数据对FFRLS算法进行验证,以获取锂离子电池的内部参数在不同时刻的动态变化情况,并将它们作为模型的输入得到模拟电压后与测量电压作对比以分析参数辨识精度。实验结果如图6所示。 图6 HPPC工况下参数辨识结果Fig.6 Parameter identification results under HPPC working condition 图6(a)中,U1表示测量电压值,U2表示FFRLS 在线参数辨识对应的模拟电压值。图6(b)中,Err表示模拟电压误差曲线,可以看出,在每次循环中,电流突变瞬间也即电池充放电部分的模拟误差相对较大,但仍可控制在3.46%以内,这与锂电池内部剧烈的化学反应有关,在其余阶段的模拟效果都十分良好。由实验结果可知,通过FFRLS算法可获得较高精度的在线参数辨识结果,以应用于后续的SOC估算中。 为了验证所提出算法的可行性,采用自定义DST 工况的实验数据进行验证。DST 实验步骤如下:首先,电池以1 C恒定电流进行充电,直至达到上限截止电压4.2 V。充电完成后,将电池搁置30 min以稳定电压。再对其以0.5 C速率进行恒流放电和恒流充电4 min,然后以1 C 速率进行恒流放电4 min。循环这3 个步骤直至放电结束。新息数据宽度p要根据多次调试来确定最佳取值,比较不同取值下的估算效果,该工况下令p=4,SOC估算初始值设置为0.95,EKF、AEKF 和加权多新息AEKF在DST工况下的仿真结果如图7所示。 图7 DST工况下SOC估算结果Fig.7 SOC estimation results under DST operating condition 在图7(a)中,SOC1表示实际SOC值,SOC2表示基于EKF算法的SOC估计值,SOC3表示基于AEKF算法的SOC估计值,SOC4表示基于加权多新息AEKF算法的SOC估计值。图7(b)中的Err1~Err3 分别表示与图7(a)中SOC2~SOC4 相对应的估算误差。在放电后期,电池SOC 估算值波动较大,产生误差的累积,这与电池自身内部化学反应有关,但Err3 明显要比Err1 和Err2 具有更好的收敛性,能较好地跟踪真实值,误差可控制在1.94%以内,EKF误差则高达3.89%,且误差有明显增大趋势。在DST 工况下,通过平均绝对误差(MAE,mean absolute error)和均方根误差(RMSE,rootmean-square error)对3 种算法的估算结果进行对比,见表1。 表1 DST工况下不同算法SOC的估算比较Table 1 Comparison of experimental results of different algorithms under DST working condition BBDST工况来自北京公交动态测试的真实数据采集,包含汽车在启动、滑行、加速、急加速等多种操作下的数据,具有真实性和动态性,而大功率锂电池的实际应用工况是复杂多变的,采用BBDST实验数据来对算法进行可行性验证会更有说服力。完整BBDST工况的电压状态变化如图8所示。 图8 BBDST工况Fig.8 BBDST working condition 该工况下令新息数据宽度p=4,SOC估算初始值设置为0.95,EKF、AEKF 和加权多新息AEKF在BBDST工况下的仿真结果如图9所示。 在图9(a)中,SOC1 表示实际SOC 值,SOC2表示基于EKF 算法的SOC 估计值,SOC3 表示基于AEKF算法的SOC估计值,SOC4表示基于加权多新息AEKF算法的SOC估计值。图9(b)中的Err1~Err3 分别表示与图9(a)中SOC2~SOC4 相对应的估算误差,在放电前期,3 条误差曲线重合度较高,Err3略优于前两种算法。在放电后期,EKF估算结果产生较大偏差,误差累积现象明显,高达4.19%。AEKF 的估算精度明显优于EKF,后期稳定性有所提高,误差最大可至2.49%。加权多新息AEKF算法具有最佳性能,在完整实验过程中模拟值偏离真实值始终较小,且误差始终呈收敛趋势,末期在0附近上下波动,在放电末期电池内部化学反应强烈的情况下,误差最高也仅为1.17%。在BBDST 工况下,通过MAE 和RMSE 对3 种算法的估算结果进行对比,见表2。 图9 BBDST工况下SOC估算结果Fig.9 SOC estimation results under BBDST operating condition 表2 BBDST工况下不同算法SOC的估算比较Table 2 Comparison of experimental results of different algorithms under BBDST working condition 通过在上述两种复杂工况下对算法的实验验证可知,相比于传统EKF,AEKF增加了自适应调节效果,能减少误差的积累,在一定程度上增强算法的跟踪能力。加权多新息AEKF极大克服了传统算法的后期易发散问题,大大提高了电池SOC 估算精度和算法稳定性。通过算法间在MAE 和RMSE上的比较可知,加权多新息AEKF的估算效果在整体上偏离真实值较小,离散程度小。 大功率锂离子电池荷电状态的精确估计对新能源汽车的应用和发展具有重要意义。本文采用二阶RC等效模型来表征电池的动态特性,采用FFRLS进行在线参数辨识,得出电池内部参数和SOC 间的动态变化关系。为了提高SOC 估算精度,本文创新性地提出了一种加权多新息AEKF方法,该算法充分利用多个时刻的残差信息并根据包含信息量的不同为其配置相应权值,且具有良好的自适应调节和校正功能。利用DST和BBDST两种复杂工况下实验数据进行验证,结果表明,该算法的估算均方根误差可分别控制在1.31%和1.23%,与传统算法相比,估算精度和稳定性都有明显提升。本文的研究内容对锂电池的状态监测和新能源汽车的长远发展具有积极意义。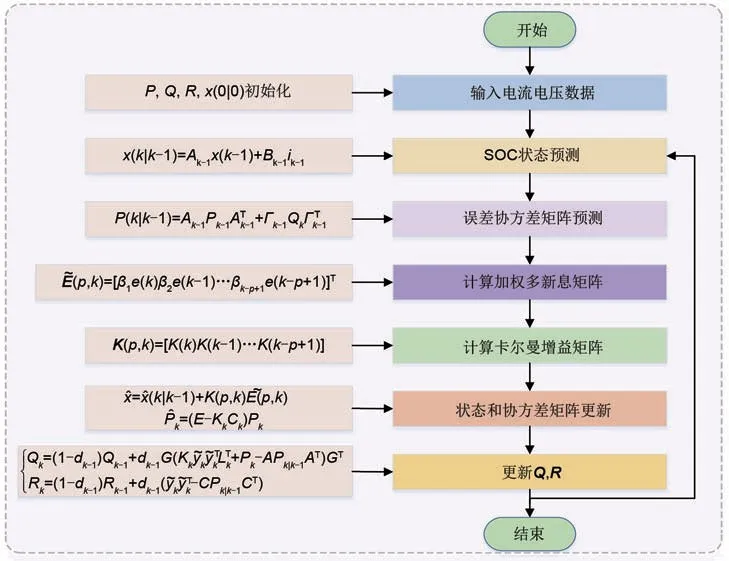
2 实验结果分析
2.1 实验平台搭建

2.2 在线参数辨识结果
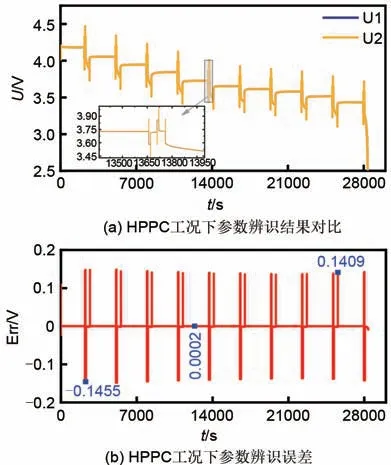
2.3 DST工况实验验证


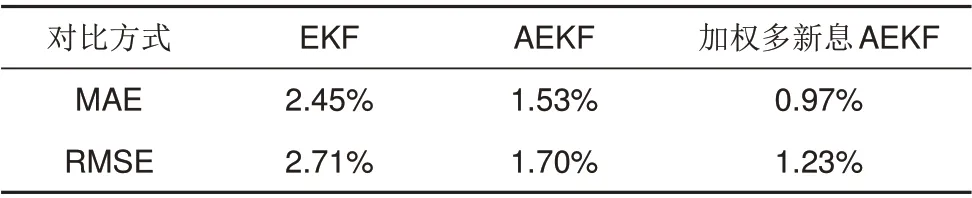
2.4 BBDST工况实验验证


3 结论
