无界弹性介质球形液体空腔中的气泡的动力学*

张先梅 王成会 郭建中 莫润阳 胡静 陈时

(陕西师范大学,超声学重点实验室,西安 710062)

构建了弹性介质包裹的液体腔内的气泡振动模型,并基于压力平衡关系得到了腔内液体中气核发展成为空化泡的Blake 阈值以及液体腔临界半径表达式.体积模量、泡核半径及表面张力系数等因素可影响Blake 阈值压力和气泡大小,形成触发或抑制空化发生的控制条件相关的参数空间.基于拉格朗日方程推导了考虑腔外介质弹性影响的气泡动力学方程,并基于此分析了激励声波频率、介质体积模量、腔内液体体积等因素对气泡振动行为的影响,结果表明:在声场驱动下,泡核快速生长到新的平衡半径后振荡;气泡平衡半径与超声无关,但会影响气泡动力学行为.当超声频率与气泡固有振荡频率相当时,气泡在几个周期的剧烈振动后崩溃,同时在腔内液体中形成明显的压力起伏变化.高频超声驱动下气泡的响应相对较弱,气泡主要表现为自由振荡.

1 引言

超声空化效应主要表现为液体中存在的微小气泡(空化核)在声波作用下产生振荡、扩大、收缩至内爆等一系列现象的动力学过程.在气泡坍缩的瞬间,泡内聚集的能量迅速释放,使得在空化发生的微小空间内呈现高温、高压、冲击波、微射流及发光等物理现象.空化现象广泛存在于自然界[1]且在水利[2]、化工[3]、医学[4]、核工业[5]等诸多领域,有着重要的应用价值.目前,超声治疗是颇具前景的非侵入性治疗技术,其中高强度超声治疗可用于治疗实体肿瘤[6]、前列腺病理[7]和生物膜感染[8]等疾病,而低强度脉冲超声主要用于非肿瘤性疾病的辅助或康复治疗[9].高、低强度超声治疗效果均可能与空化效应相关.强度低时,气泡表面存在较小的速度梯度和微弱的黏滞力,微小气泡呼吸样的膨胀与收缩使气泡周围的胞质流动性增加,物质交换加快,细胞新陈代谢增强;强度高时,微小气泡瞬间崩溃,可产生高速冲击波和射流使空化中心周围的生物大分子受到的应力增加以达到治疗目的[9].实验研究受限于时间与空间分辨率且较难在真实组织中观察空化事件[10,11],本研究旨在通过建立简单的模型对组织内空化成核及动力学影响因素进行讨论,为利用空化效应进行超声治疗提供理论参考.

近年来,由于超声治疗技术的发展,生物组织内的空化效应越来越受到人们的关注.基于无界液体内描述单气泡动力学的Keller-Miksis 方程[12],Drysdale 等[13]发展了弹性介质包裹的液体腔内的气泡动力学模型,对空腔中真空气泡的线性(小振幅)振荡衰减进行研究.Doinikov 和Marmottant[14]为分析气泡自然振荡行为,在Drysdale 等[13]模型的基础上考虑空腔周围介质黏性与气泡内介质质量及成分(一种气体和蒸汽的混合物),提出了黏弹性介质包裹的液体腔内的球形气泡脉动理论.在Doinikov 和Marmottant[14]模型上,Doinikov 等[15]不考虑介质黏性继续研究球腔内的非线性气泡动力学理论,推导出球形液体腔中空化气泡动力学方程,分析了气泡生长和阻尼振荡规律.Wang[16]建立了1 个描述在弹性固体约束下空腔内气泡振动的理论模型,分析了气泡振荡及共振频率,在此基础上,张陶然等[17]考虑组织黏弹性对腔内气泡的影响,引入Voigt 黏弹性模型,分析了介质黏弹性对气泡共振频率、径向振动及惯性空化阈值的影响.

基于弹性介质包裹的液体腔内的气泡动力学模型,Vincent[18-20]对凝胶中充满水的空腔内自发或触发的气泡空化动力学进行了实验研究,通过光散射、激光频闪摄影等对凝胶空腔中空化气泡行为进行成像记录,发现气泡的振动不仅受到泡内气体弹性的影响,液体和腔外介质的可压缩性的影响也至关重要,可导致气泡振荡速度变快;基于实验的理论分析还发现液体的可压缩性及介质弹性导致了气泡径向快速振荡和衰减.

Leonov 和Akhatov[21]建立了1 个描述刚性微腔内的气泡振动模型,在此基础上,对刚性微腔中气泡的Blake 阈值模型进行修正并推导了气泡动力学方程.生物组织中的空化行为可视作是被弹性介质包裹的液体腔内空化气泡的动力学效应,因此,本文在Leonov 和Akhatov[21]工作的基础上,考虑腔外弹性介质,构建弹性介质包裹的液体腔内的气泡振动模型,并基于此修正了弹性介质包裹的液体腔内的气泡的Blake 阈值模型,分析了激励声波频率、介质体积模量、腔内液体体积等因素对气泡振动行为的影响.

2 Blake 阈值

2.1 Blake 阈值

空化现象常见于液体环境中.液体中的声波压力幅度足够大,所产生的负压足够低,可破坏液体结构形成空腔进而发生空化效应.经典Blake 阈值模型可预测无界液体中的力学不稳定性,即气核快速生长为空化泡并发生稳态或瞬态空化过程.经典Blake 阈值模型假设:在无限大的液体中有1 个半径为Rb的球形气泡核,泡内含有一定量的不凝结气体,考虑系统为“等温系统”—热力学系统始末态温度相等且等于环境温度、在整个过程中环境温度不变的热力学过程,也就是不存在外部施加的温度梯度,也不考虑由膨胀、收缩或黏性引起的明显温度变化.因此,可假定饱和蒸汽压Pv(T) 为常数.

根据气泡表面压力平衡可得到压力平衡方程[21]

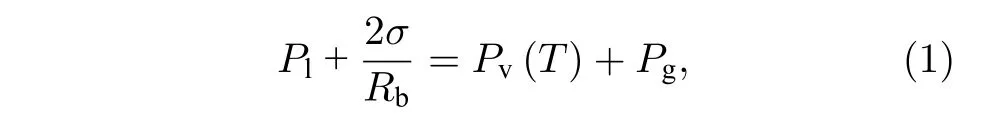
式中,σ为表面张力系数,Pl为液体压力,假定在参考状态下,半径为Rb0的泡核在环境液体压力P0下是稳定的,(给出气泡内气压[21])

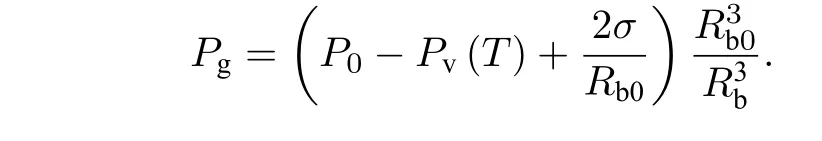
2.2 修正的Blake 空化阈值模型

为研究生物组织内的空化问题,基于经典Blake阈值理论,发展弹性介质内液体腔中Blake空化阈值理论,其准静态变化过程如图1 所示.假设空腔内充满可压缩的黏性液体,空腔周围介质为弹性固体,气泡内部介质是气体和液体蒸汽的混合物.弹性介质、液体腔及泡核组成的系统在负压作用下,经历图1 所示的过程.初始时(图1(a)所示),液体腔内液体压力等于大气压P0,未受扰动液体腔半径为Rc0,泡核半径为Rb0且常压下保持稳定.在负压Pl1作用下液体腔半径拉伸至Rc使得Rc＞Rc0(图1(b)所示),而后液体腔内泡核增长至Rb使得Rb＞Rb0(图1(c)所示).为简化分析,本文仅考虑介质在应力作用下发生线性变化的情形,假定腔外弹性介质体积模量Kc、腔内液体体积模量Kl,二者均为常数.

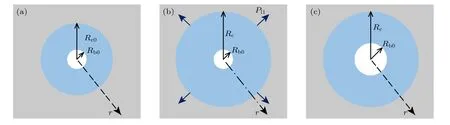
图1 系统准静态示意图(空腔中气核在负压 Pl1 下生长) (a) 初始状态,未受扰动;(b)液体腔在负压下被拉伸;(c) 气核生长Fig.1.Configuration of the quasi-static motion of the system (schematically).The cavity contains a bubble nucleus,which grows under tension Pl1 :(a) Initial state,unperturbed;(b) the cavity stretched under tension;(c) a bubble nucleus grows.

为求解液体腔内液体压力,假设腔内液体均匀分布,即可用液体腔内壁处压力近似等于液体压力.假设气泡体积远小于液体腔体积,液体腔体积变化与液体腔内壁处压力变化呈线性关系[12],则有

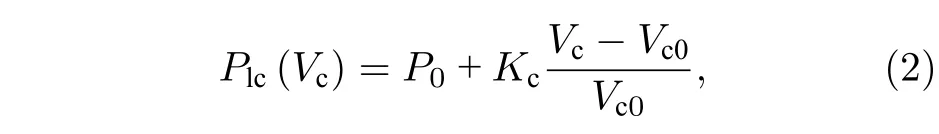
其中Vc0和Vc分别为腔体初始体积和瞬态体积,Plc为液体腔内壁处的瞬态液体压力,Plc=Pl(Rc,t) .同理,液体腔内液体体积变化与液体腔内壁处压力变化呈正比[12],则有

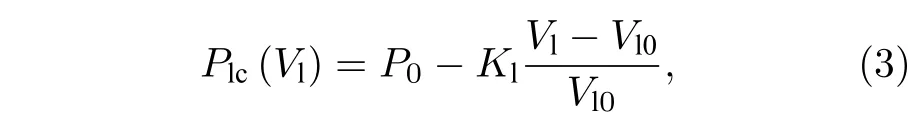
式中,Vl0和Vl分别为液体腔内液体初始体积和瞬态体积.

分两步求空化泡形成后液体腔内壁处液体压力,首先,假定液体腔在超声负压Pl1作用下均匀膨胀至Rc＞Rc0,如图1(a)→图1(b)所示.液体腔内液体瞬态与初始体积分别为,结合（3）式,此时,液体腔内壁处液体压力可表示为

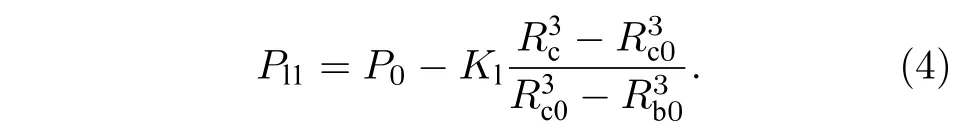
随后,泡核在张力作用下生长,如图1(b)→图1(c)所示.液体腔瞬态和初始体积分别为Vc=,随着液体体积模量Kl和弹性介质体积模量Kc增大而增大的系统有效体积模量K=KcKl/(Kc+Kl),结合(2)式和(3)式,液体压力可表示为[20]

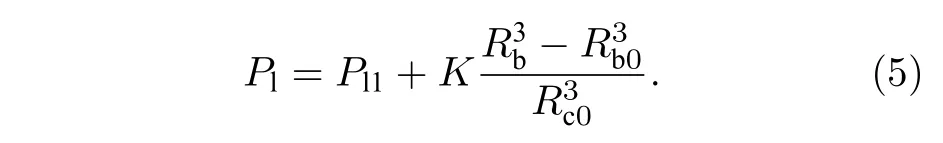
系统在经历上述过程后,液体腔内液体压力为

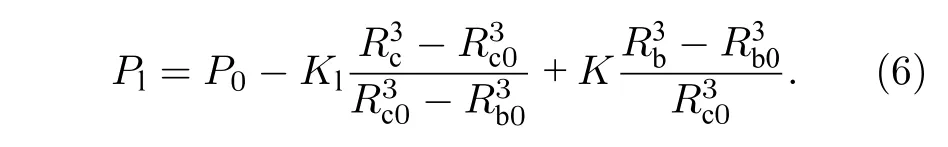
气泡处于稳定状态时,液体的压力Pl、表面张力 2σ/Rb、泡内气体压力Pg及液体饱和蒸气压Pv(T)存在动力平衡,即

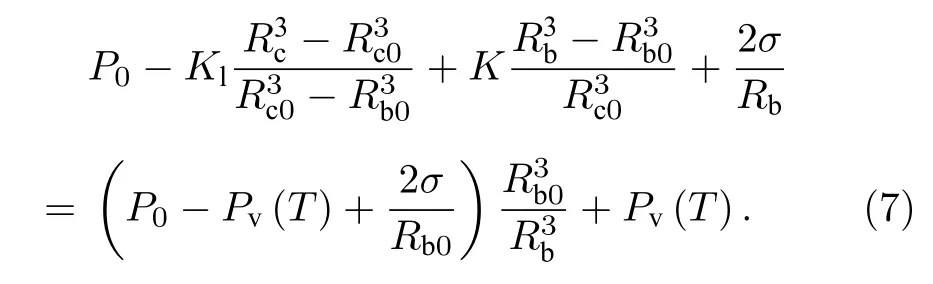
为了简化分析,将(7)式改写为无量纲形式

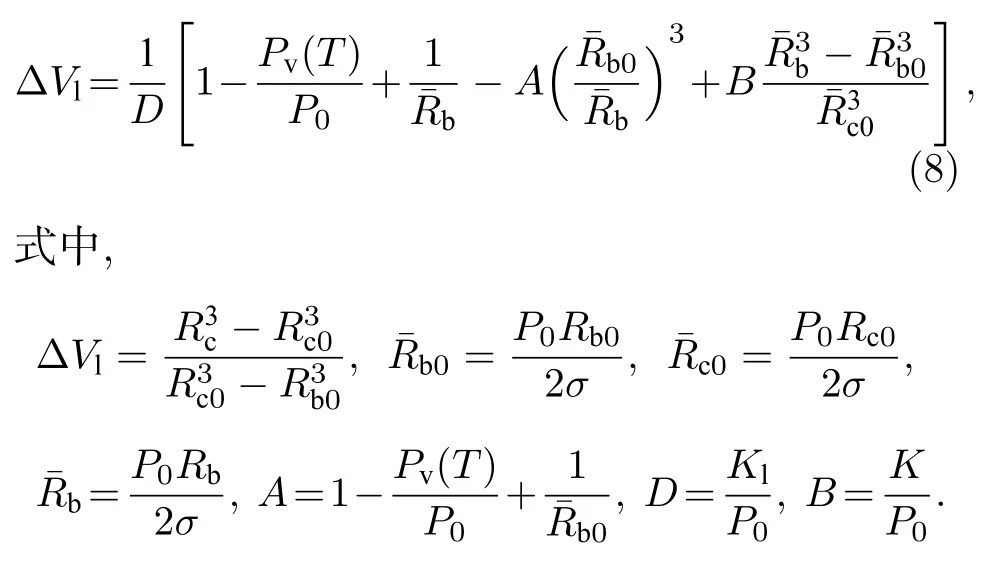
弹性介质约束条件下空化发生的泡核临界半径满足 d(ΔVl)/=0,则

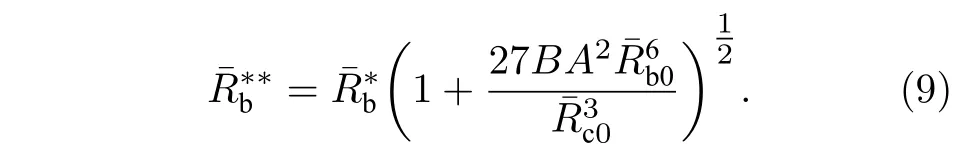
假定腔内液体为水,泡内气体为空气,常温常压下有Pv(T)=2338 Pa,P0=105Pa,σ=0.0728 N/m,腔外介质为软组织且相关参数参考文献[22],即ρs=1060 kg/m3,cs=1540 m/s,泡核和液体腔初始半径分别为Rb0=100 nm,Rc0=40 μm,腔外弹性介质体积模量.对比分析弹性介质腔内液体体积变化曲线与无界液体中的平衡压力曲线[20]可知,图2(a)中状态A对应气泡核处于稳定平衡状态,即当环境压力存在扰动时,泡核有向该状态平衡半径演变的趋势;状态B给出泡核临界半径和空化阈值压力,此时泡核不稳定,其大小可迅速膨胀至状态D对应的半径,表明空化现象已经发生.对处于状态D点的气泡而言,如果液体腔体积 ΔVlc增加,气泡半径将会不断增大;若液体腔变小,泡核可减小至状态C对应的平衡半径,并急速坍缩到状态A对应的稳定平衡半径.由(5)式可知,液体负压环境下泡核将生长,当泡核从状态B跃变到状态D时,液体压力将得到释放,液体体积 ΔVlc减小引起的相反的张力作用可导致液体压力从状态D减小至亚稳态C,进而突变至状态A.因此,空化环境中含气核的液体体积减小时液体内压力的变化存在不连续变化的情形.

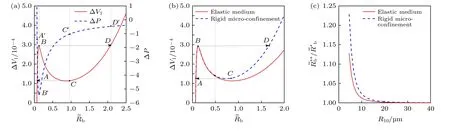
图2(a) 腔内液体体积变化曲线与无界液体中的平衡压力曲线对比;刚性微腔与弹性介质中的球腔内液体空化模型对比,其中图(b)是腔体体积变化量与气泡平衡半径的关系,图(c)是气泡Blake 阈值半径随腔体半径的变化关系Fig.2.(a) Comparison of the curve of the volume change of the liquid in the cavity and the equilibrium curve of the bubble in unbounded liquid.Comparison of cavitation models of liquid in spherical cavity between rigid microcavity and elastic medium:(b) The dependence of the relative change of liquid volume on the equilibrium bubble radius;(c) the dependence of the Blake threshold radius on the cavity radius.

为比较腔外介质形态对空化阈值的影响,将本文修正的Blake 阈值模型与Leonov 和Akhatov[21]在分析刚性微腔内液体空化模型进行了对比,结果表明:在其他参数一定的情形下,在无量纲平衡半径大于0.5 的范围内,弹性介质腔内的液体体积变化小于刚性腔体内的液体体积变化(图2(b));而在腔体半径小于20 μm 时,气泡平衡半径小于刚性腔内的气泡平衡半径(图2(c)).由此可以看出,弹性约束不影响泡核的临界半径,但是可影响泡核从临界状态跃变生长可达到的最大半径,因此,弹性约束环境下泡核更容易形成空化影响.

介质体积模量可影响空化泡生长的阈值压力和最大半径,如图3 所示.图3(a)给出了腔外介质体积模量分别为0.1,2.5 和5 GPa 时的液体体积随气泡平衡半径变化曲线,对比发现,腔外介质体积模量的增加不影响气泡阈值半径,但气泡的稳定平衡半径会随着腔外介质体积模量的增加而减小,气泡能够达到的最大半径随着腔外体积模量的增加而减小.液体体积模量的变化对空化行为影响更为显著,对比图3(b)中液体体积模量分别为1,2.2 和3 GPa 时的 ΔVlc响应曲线发现,液体体积模量Kl越小,临界气泡半径对应的液体体积变化量越大,意味着气泡更难以生长到临界状态.因此,约束状态下,液体的体积模量越小,空化发生所需的阈值压力越高,空化更不易发生.因此,在超声治疗时,组织液的体积模量大小将影响空化初生的难易程度.然而,一旦空化发生,体积模量越小时空化气泡半径越大,越容易形成空化影响.

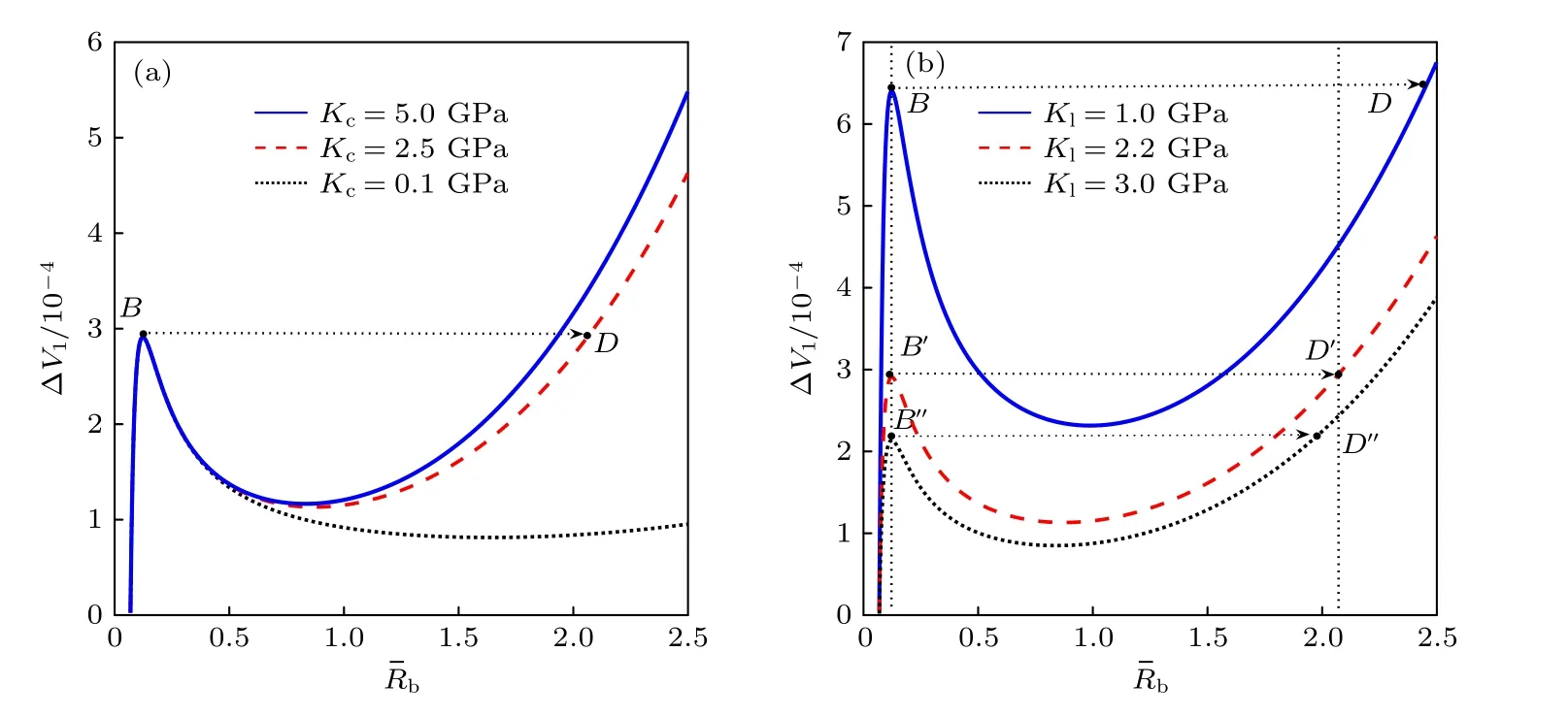
图3 体积模量对平衡半径的影响 (a) 腔外介质体积模量;(b) 液体体积模量Fig.3.Influence of bulk modulus on equilibrium radius:(a) Influence of the bulk modulus of the medium outside the cavity;(b) influence of liquid bulk modulus.

液体腔初始半径大小会影响空化后的气泡的行为响应.图4(a)给出了不同液体腔半径下,液体体积随气泡平衡半径变化曲线,对比发现,空化泡的大小随腔体初始体积的增大而增大,当Rc0→∞时,气泡平衡半径趋于无穷,这与无束缚液体中空化情况相对应;当Rc0→Rb0时,曲线变成单调递增曲线,而此时的空腔初始半径满足

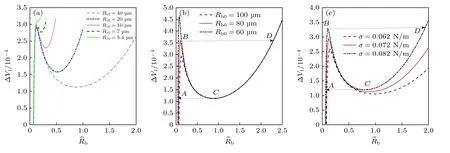
图4 不同初始半径及表面张力系数下气泡的平衡图 (a)腔体初始半径;(b)泡核半径;(c)表面张力系数Fig.4.Equilibrium diagram of the bubble for the different Initial radius and surface tension:(a) Initial radius of cavity;(b) the radius of the bubble nucleus;(c) surface tension coefficient.

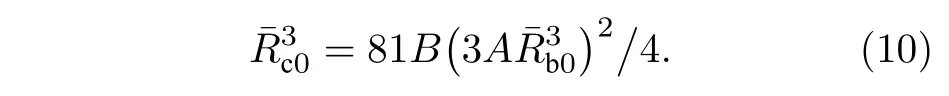
腔体初始半径越小越不容易空化,若小于(10)式给出的腔体半径值时,将不会发生空化.(10)式给出了弹性介质内的球形液体腔中发生空化的空腔临界半径.Vincent 等[23]对实验观察了凝胶包裹的液体腔内的气泡数目,发现液体腔半径越小,气泡数目越少,这与本文得到的泡核初生模型预测的液体腔越小越难空化的结论一致.由于泡核稳定时,外加负压需要克服表面张力影响,因此,泡核初始半径与表面张力系数决定空化临界半径,从图4(b)给出的泡核半径分别为100,80 和60 nm 时的液体体积变化量随气泡平衡半径的变化曲线发现,泡核越小,表面张力越大,需要更大负压才能达到空化阈值且阈值半径越小.同样,数值分析表明,表面张力系数越大,空化阈值压力越大,泡核空化阈值半径越小(图4(c)).

3 超声对弹性介质内球形液腔内气泡的动力学影响

由于空腔体积非常小,可假定空腔内液体在空间上均匀分布,但液体压力和密度随时间可变Pl=Pl(t),ρl=ρl(t) .忽略腔内液体蒸发或冷凝,假设液体质量守恒.借鉴Leonov 和Akhatov[21]在分析刚性微腔内气泡非线性动力学的方法,基于连续性方程与带耗散项的拉格朗日方程推导弹性介质内球形液腔内气泡动力学方程,即

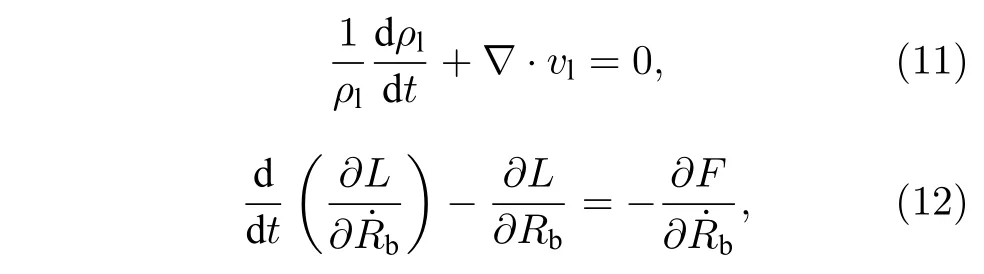
式中,ρl为液体密度,vl为液体速度矢量,L为拉格朗日量,F为耗散函数[21],表示Rb对时间t求导.

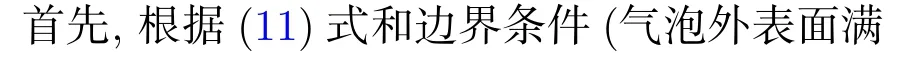
其次,腔内液体和气泡总势能可表示为

其中,PA(t) 为驱动外力.

根据(14)式和(16)式可得空腔内液体与气泡组成的系统的拉格朗日量(L=Ek-ΔW),代入(12)式即可得到球形液腔中考虑液体介质黏性耗散影响后的气泡动力学方程为

为分析超声对液体腔中气泡的动力学的影响,假定气泡所受的声驱动压力关系为

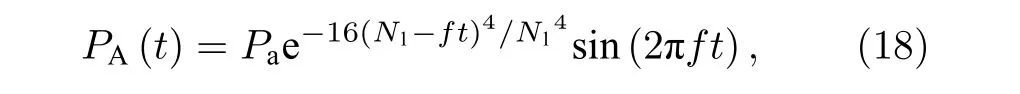
式中参数取值参考HIFU (high intensity focused ultrasound)治疗中常用的驱动频率3.5 MHz,声压幅值1 MPa,N1=10,泡核和腔体初始半径分别为Rb0=1 μm,Rc0=30 μm,腔外介质体积模量Kc=2.5 GPa .当液体腔环境压力发生变化,气核半径也会变化,形成振荡响应并趋于新的平衡半径,且振荡响应随时间增加变弱,但振荡频率随时间变化不大.液体腔外弹性介质体积模量越小,形成的振荡响应越强,气核平衡半径变化越明显(图5(a));小空腔约束对振荡响应影响更为显著,腔体初始半径与泡核比值越小,气泡振荡越弱,气核平衡半径变化越小(图6(a)),这与Wang[16]的结果相符.超声波能够激发气泡振荡,但不影响气泡平衡半径.图5(b)分析了超声作用下腔外体积模量Kc分别为0.1,2.5 和5 GPa 时气泡半径随时间的变化曲线,对比发现,当Kc为2.5 GPa 时,腔内气泡剧烈振荡且在几个周期后破裂,意味着此时超声频率最接近于气泡固有振荡频率,气泡发生共振现象,在图6(b)中也观察到了同样的现象,说明腔体约束可影响气泡的共振行为.

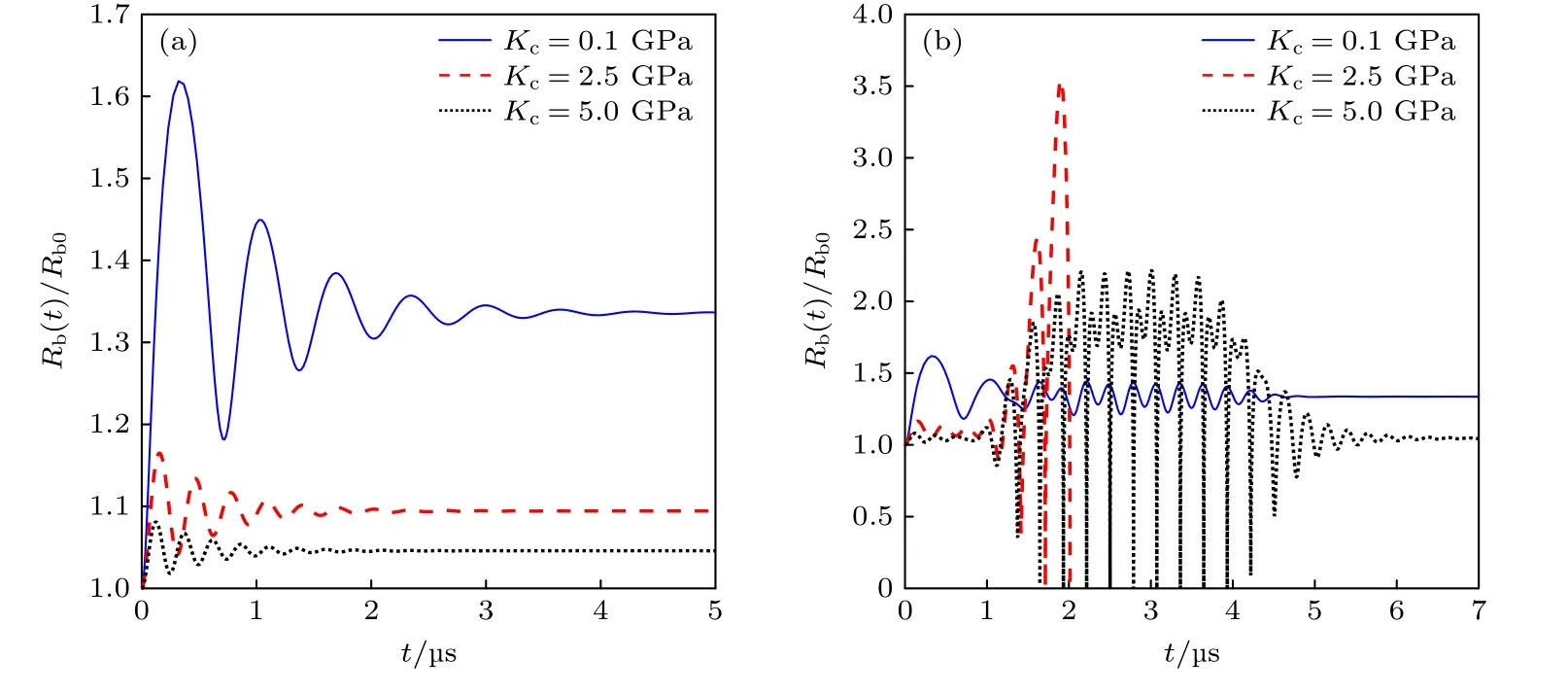
图5 腔外介质体积模量对空化泡振动行为的影响 (a)空腔中气泡瞬态振荡;(b)超声作用下空腔中气泡振荡Fig.5.Influence of volume modulus of medium outside cavity on vibration behavior:(a) A transient bubble oscillating in a cavity;(b) a bubble in a confinement subject to an acoustic wave.

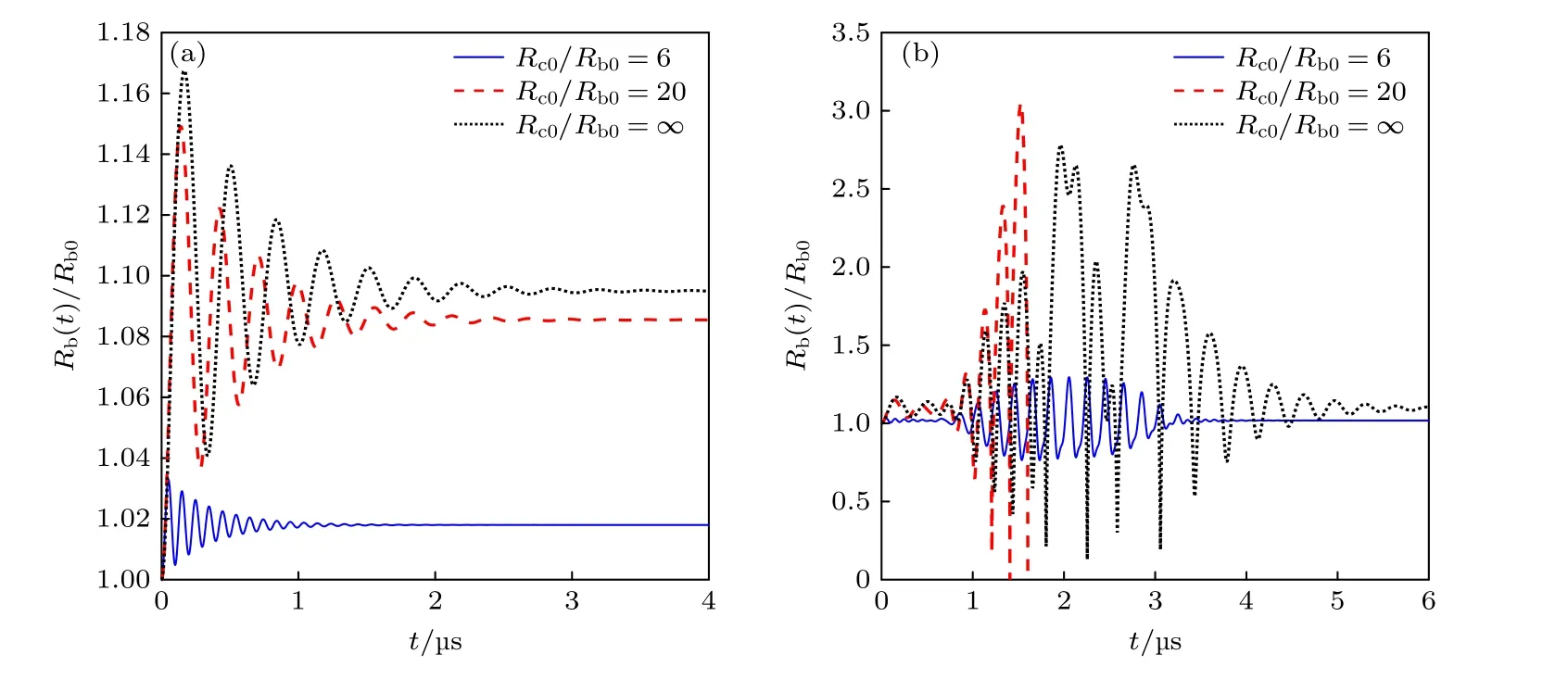
图6 不同Rc0/Rb0 取值对空化泡振动行为的影响 (a)空腔中气泡瞬态振荡的影响;(b)超声作用下空腔中气泡振荡的影响Fig.6.Influence of different values of Rc0 /Rb0 on the vibration behavior:(a) A transient bubble oscillating in a cavity;(b) a bubble in a confinement subject to an acoustic wave.

不同频率的超声波作用于腔内气泡形成的振荡响应不同,当腔内气泡发生共振响应时,气泡振动对腔内液体压强扰动最大,如图7(a)所示.气泡的响应同驱动超声的频率密切相关,在本文给定的波函数的驱动下,随着驱动声波频率的不同,气泡声响应程度不同,在低频区域内,声波对气泡的影响更为显著(图7(a)、图7(b));在驱动声波频率远高于气泡共振频率时,气泡的振动受声波的影响较小,主要表现为自由振荡(图7(d)).因此,在利用中低强度超声进行治疗时,可以调节超声频率使组织液压强变化位于合适范围,以达到治疗目的.

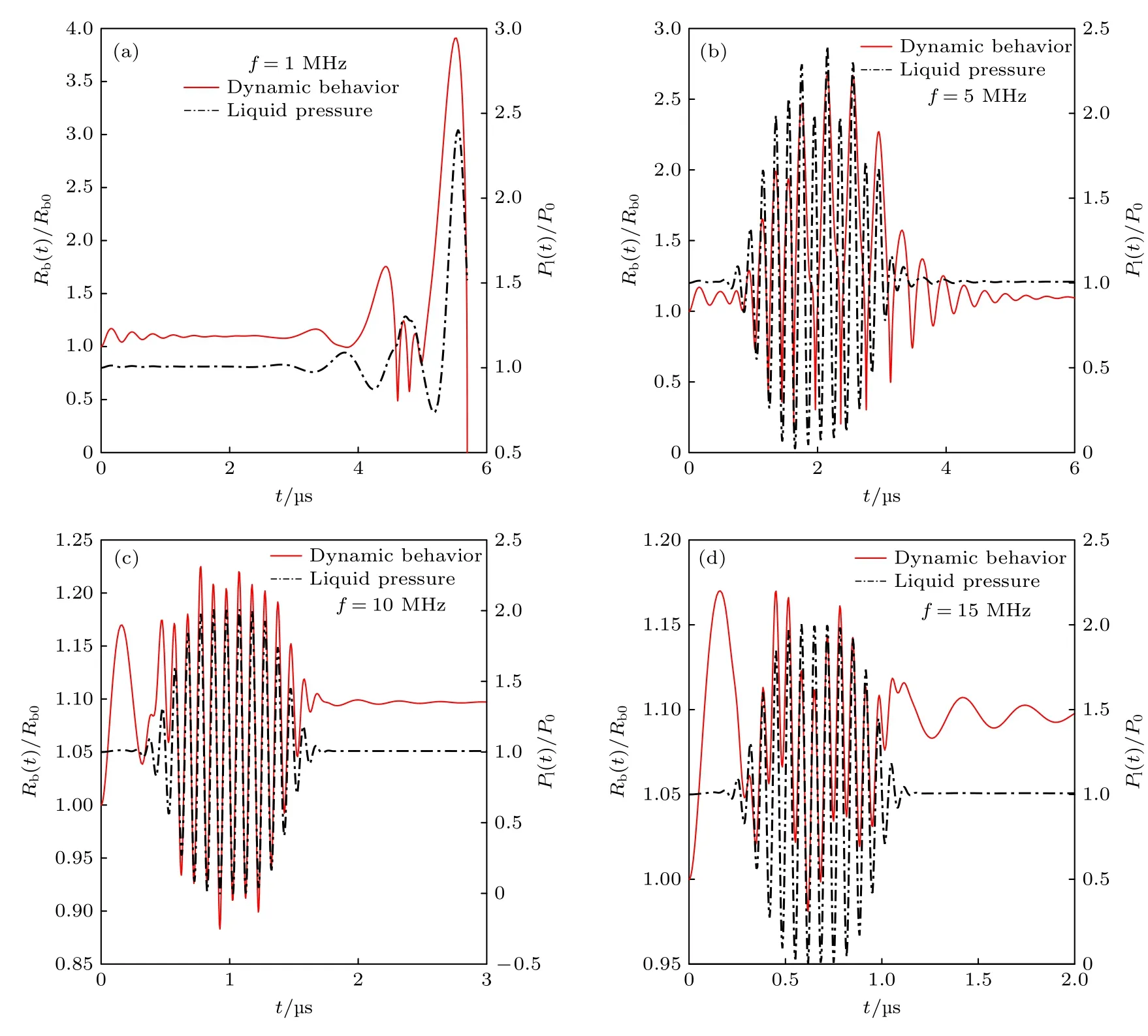
图7 不同频率外加驱动信号下气泡半径与液体压力的变化 (a) f=1 MHz;(b) f=5 MHz;(c) f=10 MHz;(d) f=15 MHzFig.7.Evolution of bubble radius and liquid pressure profiles at different driving frequencies:(a) f=1 MHz;(b) f=5 MHz;(c) f=10 MHz;(d) f=15 MHz.

4 结论

本文利用压力平衡关系得到弹性介质包裹的液腔内液体中气核发展成为空化泡的Blake 阈值,分析了泡核半径、腔体初始半径、表面张力系数及有效体积模量对空化初生的影响.在驱动力一定的条件下,泡核半径越小,空化阈值越高,阈值半径越小;表面张力系数大,空化阈值高,阈值半径越小;介质有效体积模量不影响气泡阈值半径,但液体体积模量越大,空化阈值越小;腔外弹性介质体积模量越大,空化气泡半径越小;小空腔中泡核较难形成空化气泡.

考虑液体介质黏性耗散和腔体约束影响,推导了液体腔内的气泡动力学方程,分析了超声驱动下气泡的振动响应,发现当超声信号频率与气泡固有振荡频率相当时,气泡在几个周期的剧烈振动后崩溃,同时在腔内液体中形成明显的压力起伏变化.高频超声驱动下气泡的响应相对较弱,气泡主要表现为自由振荡.弹性介质内液体腔中的气泡动力学分析在生物医学超声领域具有重要的意义,本文的研究可为中低强度空化的激励以及超声波人体应用的安全性评估提供理论支持.