基于AHP的新建地方本科院校学生考研择校研究

常丽娜，张 莉，王杏茹

(长治学院数学系，山西长治 046011)

随着高校扩招，就业竞争日益激烈，考研人数呈逐年上升态势，尤其是近年来考研人数一直快速增长，2020年考研人数首次突破300万。新建地方本科院校因办学或升本时间较短、所处区位劣势、师资力量相对薄弱，所以越来越多的新建地方本科院校毕业生为了改变学校背景、提升就业竞争力等因素最终选择了考研，在这类院校很多专业的考研报考率高达90%，但很多毕业生因为报考时盲目冲高、扎堆、追求名校，导致考研不成功，所以考研院校的科学选择尤为重要。胡平等[1]主要研究了义务教育阶段的择校问题，李砚[2]研究了高考择校问题，白玉[3]等定性地给出了本科生考研择校的指导策略。为科学有效地解决学生考研择校的决策问题，通过对影响考研院校抉择因素进行分析，将考研院校分为四类，利用层次分析法，对考研择校方案进行排序得到最佳方案。

1 毕业生考研择校决策模型构建

1.1 研究方法

层次分析法（简称AHP）是美国运筹学家萨蒂（T.L.Saaty）教授于20世纪70年代初提出的，主要是把复杂问题进行分解，然后按层次划分，寻找它们之间的内在关系，建立成对比较矩阵，将定性问题定量分析，从而确定供决策的各方案相对于总目标的权重排序，形成一个理性的、有条理的数学模型[4]。

1.2 影响因素分析

影响大学生考研择校的因素非常多，通过问卷调查及专家打分的方式将考研择校影响因素分为四类，分别是自身方面、学校实力、前景和学校政策与服务。

1.2.1 自身方面

（1）自身实力。考生自己的学习和复习情况及对英语、政治及专业知识的掌握程度直接影响考研初试和复试成绩。

（2）校友资源。报考院校及专业有校友资源可以为考生获取考试复习资料、联系导师等。

1.2.2 学校实力

（1）学科排名：学科排名靠前，说明所属院校该学科有高层次的教师队伍、良好的学术氛围、高水平的科研能力，对培养学生的科研能力有着较大的促进作用。

（2）学校排名：一流高校可以给学生带来的荣誉感、满足感；将来就业时招聘单位在筛选简历时更容易通过；多数学生自觉性高，学习氛围较好，对学生的学习、科研有促进作用。

1.2.3 前景

（1）地理位置。一线、二线经济发达城市给学生所提供的实习机会、学术交流机会及校园招聘会都大大多于三线、四线城市，且学校位于一线、二线城市的高校毕业生更多地会留在学校所在地，所以毕业后的校友资源也较为丰富，有利于毕业后的职业发展。

（2）深造空间。在国内继续攻读博士学位、或者出国深造机会也是大学毕业生在选取考研报考院校时考虑的非常重要的一个因素。

(1)在经过处理后的数据中一共有1875位会员，将每位会员的预定限额作为第1个指标xk1。任务可以开始预定的最早时间为6：30，每位会员的开始预定时间与6:30相差mk分钟，mk=(0,3,6,,,90)。当 mk≠0 时，取

（3）就业前景。不同的院校、不同的学校背景、不同的专业直接会影响到学生的就业机会，特别是近年来就业形势日益严峻，所以就业前景是大学生在选取院校时非常关心的一个方面。

1.2.4 学校政策与服务

（1）奖助政策。在考研择校过程中，院校的奖助政策也是大学生考虑的一个因素，特别是对于家庭比较贫困的学生来说，读研过程中如果可以取得一定的奖助学金，可以一定程度上缓解家庭经济压力。

（2）招生分数段。目标院校的初试的总分数线、单科分数线是考生能否进入该高校复试、就读的重要依据。

（3）教育资源与服务。高校优渥的图书馆资源、讲座资源、学术会议、教师资源、教学设施、校园环境也是吸引考生报考院校的一大因素。

1.3 方案设定

在设定方案时主要设定新建地方本科院校多数学生最常选且能力范围内的一些高校，比如一些双一流高校兼具地理位置优越、学校声望高、就业前景好等优点，所以分数线非常高，但对多数新建地方本科院校学生来说考取相对较难，所以本文在设置方案时不予考虑。同时为了满足多数人的需要，本次方案设定没有设置具体的院校，而是设置了新建本科院校学生最常选的四类院校，分别是，学校1：一线城市、非一流大学、非一流学科；学校2：二线城市、一流大学非一流学科；学校3：二线城市、非一流大学一流学科；学校4：三线城市、一流大学一流学科。

1.4 建立层次结构模型

将大学生考研择校问题分为四个层次，把考研院校选择作为目标层O（最高层），影响大学生考研院校选择的影响因素作为准则层（中间层），因影响因素较多，故将准则层分为两层R1、R2，不同的院校作为方案层P（最底层）。建立考研择校层次结构模型如图1所示。

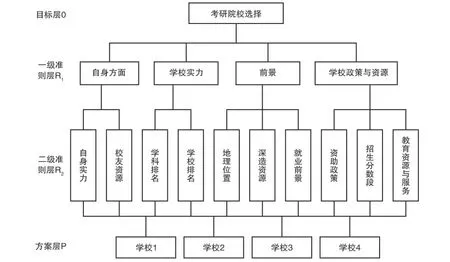
图1 考研择校层次结构模型

2 实证分析

2.1 数据来源及处理

从层次结构模型中，已经知道每个层次及其所含的影响因素，现在需得出各个因素对总目标的影响权重，这里采用构造各层次的判断矩阵，从而确定各因素对上层次各指标因素的权重。为了避免数据偏向个人主观，本文采用问卷调查及专家打分的方式，分析各个影响因素占总目标的比重，建立合适的判断矩阵，判断矩阵中的各元素aij主要采用SaTty 等人提出的1～9标度法[4]如表1给出。

表1 Satty的1～9标度法

问卷调查以长治学院考研学生为对象，主要分为两个板块，板块一是对考研学生的基本信息进行调查，板块二是针对院校选择时影响因素的重要程度进行调查。本次调查共发放问卷调查300份，收回问卷280 份，有效问卷275 份。在此次收回的有效问卷调查中，文科学生占6.34%，理科学生占83.1%，工科学生占8.1%，艺体学生占2.46%，由数据可以看出，本次调查中理科人数较多。成绩分布中处于10%−30%的学生较多。有考研打算和正在备考以及刚考完的人数比例相差不大。有59.86%的同学选择考研院校的态度为保守选择，40.14%的同学选择冲一冲，选择好的院校。

通过对问卷调查结果的分析及专家打分的修正，得出影响考研院校抉择的各个因素之间的关系，将每层各个因素对上层各项指标的影响两两比较并利用1～9标度法得到判断矩阵。

一级准则层R1对目标层O的判断矩阵为

二级准则层R2对一级准则层R1的判断矩阵，即自身方面矩阵、学校实力矩阵、前景矩阵、学校政策与资源矩阵依次为

方案层P对二级准则层R2的判断矩阵，即自身实力矩阵、校友资源矩阵、学科排名矩阵、学校排名矩阵、地理位置矩阵、深造空间矩阵、就业前景矩阵、奖助政策矩、招生分数段矩阵、教学资源与服务矩阵依次为

2.2 权重确定及一致性检验

因为在建立判断矩阵时存在一定的主观性，所以通常不是一致，其最大特征值一般不是n，故需求出判断矩阵的最大特征值及其对应的特征向量，用归一化后的特征向量作为权向量[6]。利用Matlab 软件计算各个判断矩阵的最大特征值λmax及权向量ω，确定各层次较上一层的权重并最终确定方案层较目标层的权重。

为了使得判断合理，要进一步对判断矩阵进行一致性检验。一致性检验主要通过CI和CR指标来衡量，其中为一致性指标，当CI=0时，A为一致阵；CI越大，A的不一致程度越严重，CR为一致性比率，CR=CI/RI(其中RI称为随机一致性指标，具体RI取值见表2)[3]。CR越小，说明判断矩阵越好，当CR<0.1 时，就认为判断矩阵的一致性可以接受，否则需要重新调整判断矩阵，再进行一致性检验，直到通过一致性检验[5]。各判断矩阵的一致性检验结果见表3，表3表明所有判断矩阵均通过一次性检验。

表2 随机一致性指标RI的数值

表3 判断矩阵的一致性检验结果

利用matlab 软件计算可得到一级准则层R1对目标层O的权重w(2)及二级准则层R2对一级准则层R1的权重（w(2)表示第i层相应于第1 层目标层的权重），经计算可得R1对目标层O的组合权重w(3)，见表4。方案层P相对R2的权重见表5，最后讲过计算可求得方案层P相对于目标层O的组合权重w(4)，见表5。

表4 影响因素权重表

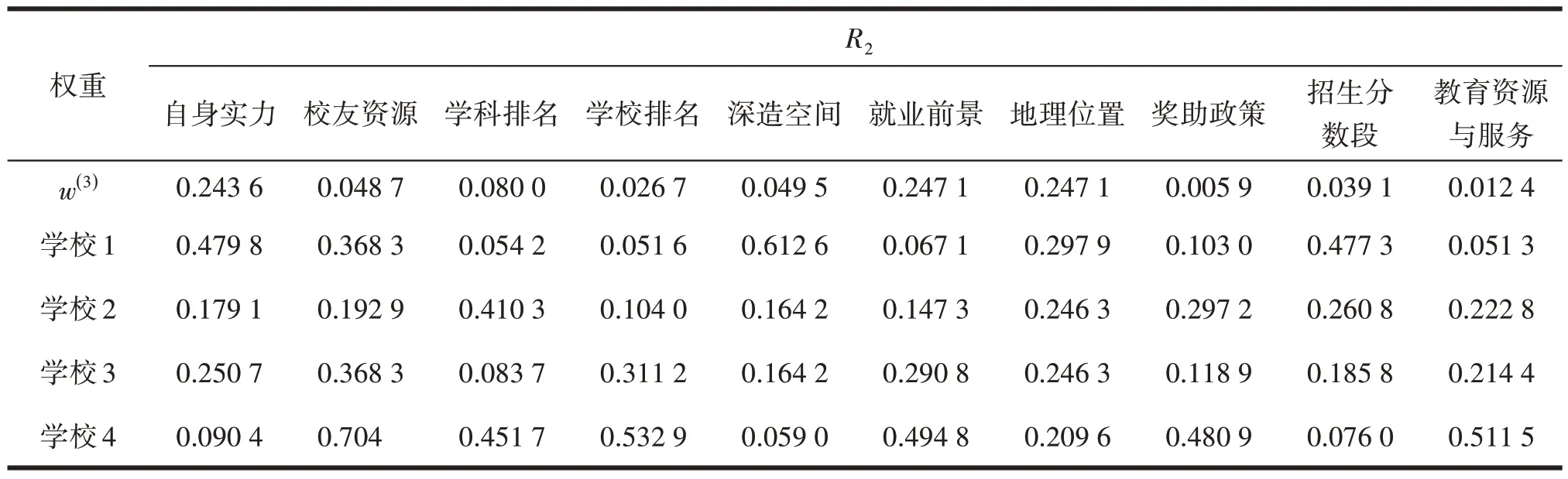
表5 方案层P对二级准则层R2的权重表

设方案层P对二级准则层R2的权重数表为矩阵W，则方案层P对目标层的权重w(4)=w(3)WT，计算得

w(4)=(0.272 5,0.202 4,0.238 1,0.287 0)

3 结果分析

从方案所占比重来看，学校4 所占比重最大，其次是学校1，说明对于新建地方本科院校的学生在考研时应首选三线城市的一流大学一流学科或者一线城市、非一流大学、非一流学科，因为新建地方本科院校的学生基础相对薄弱，所以在报考院校时可以考虑选择地理位置稍差的双一流学科院校或者选择地理位置优越的普通院校。从准则层R1的权重来看，学生在考研择校时前景所占比重最大，所占比重超过了0.5，排序依次为前景、自身实力、学校实力、学校政策与资源。从准则层R2的权重来看，就业前景、深造空间、自身实力所占必重几乎相等，排在了前三名。体现了学生在报考院校时对就业前景及深造空间的重视程度，也体现了学生自我能力提升的重要性。上研究生只是人生的一段历程，而最终的目的都是为了有一个好的前景。而所有的一切都离不开个人的努力，只有自身实力强大，才有可能考取理想的院校，获得更好的前景。

4 模型评价与推广

通过AHP 的方法，建立考研择校的一种决策体系，从新建本科院校多数学生的角度出发进行决策，尽可能的考虑到所有可能的影响因素，由判断矩阵和权重得出最终结果。通过实例的应用，为新建地方本科院校的大学毕业生在考研决策中提供合理的参考依据，同时对于考研学子在选择院校时，也能给他们提供一定的指导与帮助。在具体决策过程中决策者也可以是个人，不同的决策者会得到不同的判断矩阵，所以决策结果也不尽相同。对于方案层中的学校1、学校2、学校3、学校4，可以按类来划分，也可以选择具体的学校，针对不同的方案构建每一层具体的判断矩阵，求出总权重，从而得到最优决策。