生产率冲击、劳动力调整成本与企业劳动力资源配置
2021-11-19杨雪娇徐琰超洪名勇
杨雪娇,徐琰超,洪名勇
(云南大学 经济学院,云南 昆明 650504)
一、引言
随着中国经济步入新常态发展阶段,人口红利逐渐消失,劳动力成本低廉的优势逐步弱化,需要提高劳动力要素配置效率,创造新的人口红利。参照郭庆旺等[1]、张军等[2]全要素生产率的计算方法和郭庆旺等[3]运用HP 滤波分离出全要素生产率中的周期成分作为全要素生产率缺口的做法,用1978—2019 年的统计年鉴数据计算各年份全要素生产率的冲击发现,随着我国近年来企业经营环境不确定性增加,除了2010—2011 年全要素生产率出现短暂增长,多数年份遭遇全要素生产率负向冲击。2019 年底至2020 年,新冠肺炎疫情加剧了来自资源配置和生产效率的负向冲击。
在生产率负向冲击的宏观环境下,我国企业还面临着较高的劳动力调整成本。2008 年我国制定了《中华人民共和国劳动合同法》,规定用人单位与劳动者必须签订书面劳动合同,并在1995 年劳动法的基础上设置了更高的离职工资及补偿金标准。严苛的就业保护制度,增加了企业的雇佣和解雇成本,而这两种成本是劳动力调整成本的主要来源。在生产率冲击与劳动力调整成本的双重压力下,企业劳动力资源配置是否受到影响? 不同所有制类型企业对哪一种压力更敏感? 这些问题的解答,对于我国企业应对生产率冲击具有重要的启示作用,特别是新冠肺炎疫情下企业面临来自需求减少产生的负向生产率冲击,双重压力下的劳动力资源配置效率提升能够推进社会资源合理配置,促进经济复苏,激发企业经营活力。
现有文献研究了部门、产业、行业间的劳动力纵向流动,以及地区间、企业间的劳动力横向流动对劳动力资源配置的影响。从生产率冲击以及调整成本双重视角下,研究我国企业间劳动力配置的文献并不多见,但常见于国外一些资本配置的研究中。Asker et al.[4]使用调整成本的标准投资模型,研究了行业间生产率变动对资本边际产出变动的影响。Gopinath et al.[5]研究了南欧国家低生产率增长与利率降低并存的现象,发现利率降低导致资本流向了具有更高净值的企业而不是生产率更高的企业,造成了资本误置。国内文献中,鄢萍[6]研究了利率差异、投资不可逆以及资本调整成本对资本误置的影响。杨光等[7]研究发现生产率波动会加重资本误置的程度,而调整成本加剧了这种负向作用。研究我国劳动力配置的文献中,与本文最接近的是刘勇凤等[8]的研究,得出了劳动力调整成本使得企业生产率变动显著降低劳动力配置效率的结论,但是对于劳动力调整成本的研究仅止于调整成本系数的估计,尚未给出反事实模拟的证据,也未对企业异质性作进一步探讨。
基于此,本文结合静态和动态的分析方法,对劳动力调整成本和生产率冲击双重压力下的企业劳动资源配置展开讨论。本文的主要工作:一是运用简化式回归的方法,对生产率冲击、劳动力调整成本、劳动力资源配置之间的关系进行验证,探讨双重压力对于企业劳动资源配置的影响。二是借鉴Asker et al.[4]的做法,构建企业劳动力调整的动态估计框架,运用模拟矩估计的方法,估计劳动力调整成本函数,对比分析不同所有制企业的劳动力调整成本差异。三是通过政策模拟,构建反事实,分析生产率冲击以及调整成本的“减负”,对不同企业劳动力资源配置的异质性影响。本文的边际贡献:一是研究视角层面,将劳动力调整成本、生产率冲击与劳动力资源配置放到同一框架中,从动态和静态的角度阐述劳动力调整成本在生产率冲击与劳动力资源配置间的作用机制,为劳动力资源误置的来源分析提供了证据。二是研究内容层面,探讨双重压力对我国整体制造业企业劳动力资源配置的影响以及不同所有制企业的异质性影响,运用反事实模拟研究了来自不同方面的“减负”为我国制造业企业“增效”带来的政策效果。三是研究方法层面,将动态和静态研究方法结合,使用简化式回归和结构估计的方法,提高了论证结果的稳健性。
二、文献综述
随着人口红利逐步消失,中国的工资成本迅速上升[9]。降低劳动力成本成为企业降低成本的主要问题。但是降劳动力成本不能简单理解为降工资,工资之外的劳动力调整成本也是其重要组成部分[10]。劳动力调整成本包括与生产直接相关的内部成本,如生产流程的重新组织和人员培训,以及招聘费用、解聘费用等不直接与生产相关的外部成本[11]。
与本文相关的劳动力调整成本研究主要在于调整成本的结构估计。凸性调整成本能够反映企业小规模的要素调整以及要素调整的一致性[12]。但是其单一的结构设定却不能反映企业要素调整的大规模跳跃行为及其他异质性特征。因此,Cooper et al.[13]在企业层面构建了涵盖凸性、非凸性劳动力调整成本的动态优化模型,证实了企业层面劳动力调整成本对就业总量的影响。进一步考虑企业异质性特征时,Cooper et al.[14]用中国数据证实了劳动力调整成本在不同所有制企业间的区别。同样在中国国有企业数量大幅下降的背景下,Cooper et al.[15]从劳动力调整成本的一般均衡模型分析中发现了中国的劳动保护法规通过增加劳动力调整成本对总就业和生产率产生影响。为了使资本调整成本结构设定更贴合现实数据,近期文献也都考虑了凸性和非凸性的调整结构[6,16-18]。
本文的另一关注点在于劳动力资源错配。劳动力市场扭曲是造成劳动力资源错配的主要成因。这种劳动力市场扭曲不仅存在于日本[19]、印度[20]的农业与非农部门,也存在于我国。表现为农业与非农部门间的就业比例失衡,显著降低了TFP[21]。除了资源错配成因分析以外,要素配置扭曲程度测量也是资源错配的重要研究方向。柏培文[22]测算了我国各产业以及省际的劳动力资源扭曲程度,发现全国总体以及城乡劳动力扭曲程度呈下降趋势。董直庆等[23]对我国分行业劳动力配置的扭曲程度及其产生的全要素生产率损失进行了考察。
调整成本如何影响资源配置的研究主要集中于资本投入的调整成本方面。Asker et al.[4]运用40 个国家的数据,发现由于存在资本调整成本,使得行业间(经济体间)的生产率变动性差异能解释80%~90%的资本边际收益变动。Gopinath et al.[5]从资本流向低生产率企业的角度,解释了部分南欧国家加入欧元区后,实际利率降低导致资本错配程度增加,生产率下降的事实。David et al.[18]提出了一种分解资本错配不同来源的方法,测度了技术或信息摩擦以及其他企业异质性因素对资本错配的贡献,发现对于中国制造业企业来说,调整成本和不确定性虽然具有重要作用,但对资本错配的解释作用有限,错配的主要来源是与生产率和固定效应相关的因素。国内对调整成本与资源错配的关系研究相对较少。鄢萍[6]用模拟矩估计方法估计了中国不同所有制类型企业的资本调整成本函数,发现不同类型企业面临差别利率是资本误配置的最重要因素,资本调整成本相对次要但仍然不可忽略。杨光[7]利用调整成本的投资动态分析框架,证实了由于跨期投资中上涨的调整成本,使得生产率增长快的企业不能进行资本扩张,从而形成资源错配。刘勇凤等[8]发现由于劳动力调整成本的存在使得同一产业内企业生产率变动的差异会显著降低劳动力配置效率。刘盛宇等[24]从静态和动态角度考察了资本调整成本在生产率波动导致资本错配过程中的中介作用。
与本文联系最密切的文献为Asker et al.[4]、刘勇凤等[8]、刘盛宇等[24]。这三篇文献都是将简化式回归的静态分析与调整成本的动态模型相结合,研究调整成本对生产率波动加剧资源错配的作用机制。所不同的是刘盛宇等[24]的文章中借鉴了Zhao[25]和Hall[26]的设定,通过计算不同生产要素间的市场势力差异,估计出企业实际的资本调整成本,并采用中介作用的回归模型探讨资本调整成本的作用机制。刘勇凤等[8]、刘盛宇等[24]两篇中文文献均借鉴了Asker et al.[4]的结构估计框架和方法,构建企业动态投资模型,估计调整成本函数。本文的动态模型构建同样采用Asker et al.[4]的框架,与此前文献不同的是在企业异质性方面进行了更细致的研究,使用模拟矩估计方法识别出不同所有制类型企业的劳动力调整成本系数,并运用反事实模拟探讨了生产率冲击、劳动力调整成本的变化对不同企业劳动资源配置的作用差异,为差异化“减负增效”策略的提出提供了决策依据。
三、理论模型构建
(一)模型基本设定
本部分理论模型构建主要借鉴Asker et al.[4]的框架。假设企业为同质的生产单元,遵循规模报酬不变的生产技术。企业i在时间t的产量为Qit。

其中,Kit是资本投入,Lit是劳动力投入,Mit为中间材料,由规模报酬不变可知αK+αL+αM=1。企业产品需求曲线具有不变替代弹性,不同行业的价格弹性相等。

在市场出清的条件下,结合(1)、(2)式可推导出产品的价格函数,代入销售收入函数可知:

其中,Ωit=M},并将生产率(TFPR)定义为ωit=ln(Ωit)。假设企业的资本投入和中间材料投入均不存在调整成本,在每一期均能以价格PK和PM购买资本和获得中间材料,在生产率和劳动力约束的条件下,将静态最优条件下的资本和中间产品代入收益函数可知:

其 中,考虑企业劳动力动态投入,存在离职率的情况下,企业t时期的劳动力雇佣量为Eit-1=Lit-(1-δL)×Lit-1。进一步,遵照大多数文献(Hamermesh et al.[11];Cooper et al.[15];Bloom[17])的设定,假设劳动力调整成本函数为包含凸性和非凸性的结构:

假设下期生产率由本期生产率决定,ωit服从AR(1)形式:

其中,νit~N(0,1)独立同分布,由此决定转换函数为φ(Ωit+1|Ωit)。企业的值函数V由以下Bellman 方程给出:

(二)估计方法
与以往文献类似,基于政策函数,模拟10 000 家企业的行为,采用模拟矩估计的方法得到模拟数据的目标矩,将其与现实数据的实际矩进行比较,最小化模拟矩与现实矩之间的距离,从而识别出调整成本参数。参照Asker et al.[4]的做法,本文选取企业劳动雇佣量比例小于5%的企业比例,劳动雇佣量比例超过20%的企业比例,劳动力变化率的标准差作为目标距。之所以选择这三项指标作为目标距,是因为这些目标距对待估计的调整成本系数较敏感,并且与本文的理论假设相关。
本文的数据模拟过程是通过模拟行业内10 000家企业1 000 个月的数据,求解劳动力动态投入的最优化问题(本文中的(7)式),基于最后两年的模拟数据集来计算目标距Ψ(θ),其中表示待估参数集。同时使用现实数据计算得到实际矩根据最小化距离的判别准则((8)式)来识别出待估参数集

数值计算中需要用到的其他参数设置为:生产率服从一阶马尔可夫过程中的持续性参数ρ以及波动性参数σ,采用实际数据对(6)式进行回归得到。同时设置员工离职率δL=7.08%(Bloom[17]),折现率β=0.94(年利率为6.5%),并简化处理(4)式中的λ=1,(8)式中的权重矩阵W=I(单位阵)。
四、来自简约式回归的证据
(一)数据描述
本文使用国家统计局1998—2007 年“全部国有和规模以上非国有工业企业数据库”中的全部制造业企业作为样本,参照尹恒等[27]的方法,将不同年份的截面数据处理成面板数据,并对2002 年前后的行业代码进行了统一。将资本、投资额、销售额、中间材料、工资分别运用消费者价格指数、投资价格指数、产出价格指数、投入价格指数、消费者价格指数统一到以1998 年为基期。删除企业销售收入、就业人数、资本、中间材料投入、工资福利总额缺失或小于等于0 的样本,删除就业人数少于8 人,中间投入大于产值,出口值大于销售收入,删除要素支出大于产量值的样本,删除生产函数估计中四个主要变量上下1%极端值。
(二)行业层面生产率冲击与劳动力错配
首先从行业层面验证生产率冲击与劳动力错配的正向关系,即同一行业内企业面临的生产率冲击越大则行业内企业劳动力错配程度越大。与已有文献(柏培文[22];刘勇凤等[8];吴化斌等[10])一致,我们用行业内企业的劳动边际产出(MRPL)离散程度反映劳动力错配程度。由于在要素配置最优时,同一行业内各企业的要素边际产出相等,因此要素边际产出离散度可以用来反映要素偏离最优配置时的程度,离散度越大,错配程度越高。检验TFPR变动程度对MRPL离散度的回归模型如下:

其中,r为地区,i为行业,t为时间,Xrit为控制变量,γr+γi+γt+γri分别为控制地区、行业、时间,地区与行业组合的固定效应,νrit为随机扰动项。SDrit(MRPL)用同一时间、地区的同一行业(以下简称:同一范围)内劳动边际产出标准差来衡量。遵照Glick et al[28],吴晓芳等[29]的作法,采用行业内企业间生产率变动的标准差来反映生产率冲击,用相邻两期生产率变动的标准差(SD_VOL)来表示。另外现有研究(Asker et al.[4];吴晓芳等[29];简泽[30];李春吉[31])一般认为生产率的对数遵循一阶自回归过程,并用残差来反映生产率冲击的程度,我们采用生产率作普通一阶自回归得到的残差项(SD_AR),带固定效应以及GMM(广义矩估计)的一阶自回归残差项(分别以SD_AR_FE,SD_AR_GMM表示)作稳健性检验。涉及到劳动产出弹性及生产率的估计,本文采用OLS 方法来估计四位数行业的相应数值。
参考刘盛宇等[24],选取的控制变量包括:(1)同一范围内市场势力的标准差,反映市场垄断程度。市场势力的估计,见De Loecker et al.[32]。其中,产出弹性估计采用Ackerberg et al.[33]方法估计超越对数形式的生产函数。(2)劳动力密集度,用同一范围内企业劳动收入份额与资本收入份额占比的均值来表示。(3)参考吴化斌等[10],使用企业进入、退出比例来反映资源配置效率的变化。(4)出口密度,通过计算同一范围内企业出口产出值与总产出值占比的均值来得出。(5)净资产规模,反映企业面临生产率冲击时的抗风险能力,由同一范围内企业总资产与总负债差额取对数值后求均值得到。(6)国有企业比重。目标差异使得不同所有制企业具有了不同的劳动力调整成本[14]。因此,我们使用国家资本和集体资本在实收资本中所占比重来衡量企业的国有资本比重,并对同一范围内的企业求均值。回归结果如表1 所示。
表1 中(1)、(2)列为未加入控制变量时,对(9)式的回归结果,区别在于(2)列在(1)列基础上使用同一范围内的企业数量作为权重,进行加权回归。(3)、(4)列加入了控制变量,(4)列使用了与(2)列相同的加权回归。可以看出这四列核心解释变量的系数均在1%水平上显著为正。(5)、(6)、(7)列替换核心解释变量后,依然没有改变其系数的正显著性,只是以固定效应一阶自回归得到的系数(VOL_AR_FE)显著性有所降低,但仍然在10%水平上显著为正。从此回归结果可以看出,行业内企业遭受的生产率冲击越大,劳动力错配的程度越严重。

表1 行业层面生产率冲击与劳动力错配关系
(三)企业层面分析
本文模型的核心在于说明在企业多期动态投资过程中因为劳动力调整成本的存在,生产率冲击会导致企业之间劳动边际产出的差异。而当企业投资被设定为一期滞后模型时,如果不存在调整成本,厂商将能够根据生产率变化调整劳动力投入,这将使得厂商间劳动边际产出均等,此时生产率冲击不会对劳动边际产出的变化产生影响。为了检验这一假设,我们构建如下的回归方程:
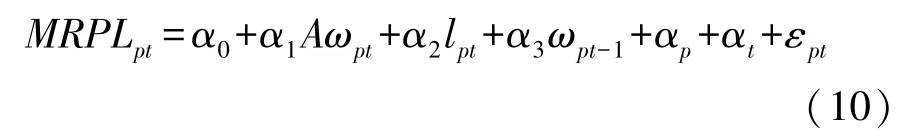
其中Aωpt为企业p在t时间受到的生产率冲击,分别用普通ols 对生产率作一阶自回归(AR),带固定效应的生产率一阶自回归(AR_FE)以及用GMM(广义矩估计)对生产率作一阶自回归(AR_GMM)所得残差来构造。为了观察t-1 期具有相同生产率的企业,在面对不同生产率冲击时,是否会造成不同劳动边际产出,对t-1 期的生产率(ωpt-1)进行了控制。此外,控制变量还包括企业t时期的劳动投入量(取对数),企业年龄,企业在中间材料市场的垄断程度,企业的国有资本比重,企业出口产值比重,劳动密集程度。对企业个体固定效应和时间效应也进行了控制。回归结果如表2 所示。
表2 中(1)至(3)列的回归结果可以看出,生产率变化的回归系数均在1%的水平上显著为正,说明企业劳动边际产出会随着生产率冲击而变化,从而拒绝了生产率冲击不会对企业劳动边际产出变动产生影响的原假设。另外滞后期生产率的系数显著为正,表明生产率冲击对资源配置的影响是一种持续的过程。
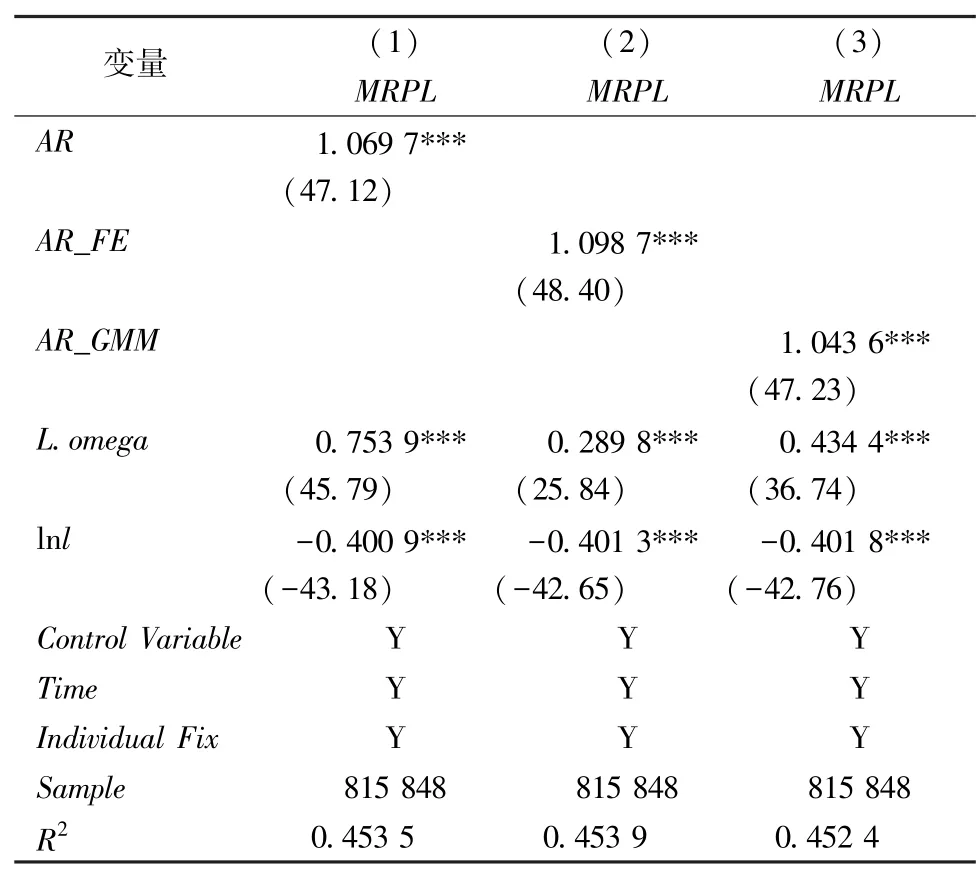
表2 企业层面生产率冲击与资源配置
(四)劳动投入量变动与生产率冲击的非线性关系
为进一步验证生产率冲击是因为存在劳动力调整成本,来影响劳动投入量的机制,本文又构建了以下回归方程:

其中,Δl=ljt-ljt-1,为同一范围内企业j前后相邻两期的劳动投入量(取对数)之差,SDrit(Δl)表示Δl的标准差。同理,SDrit(Δω)用同一范围内企业生产率差异的变动程度来反映生产率冲击,分别用SD_VOL,SD_AR,SD_AR_FE,SD_AR_GMM表示,其定义同表1 所述。Irit为虚拟变量,当SDrit(Δω)大于同一地区同一行业生产率冲击的中位数(Medianri(SDrit(Δω)))时,Irit=1,否则为0。交互项是为了检验劳动力投入量的变动是否会随着生产率冲击的增大而线性增大。回归中同时对地区固定效应、行业固定效应、时间效应、地区—行业固定效应进行了控制,其他控制变量与表1 相同。回归结果如表3 所示。
表3(1)~(4)列未加入交互项,从面板固定效应模型估计的结果中,可以看出生产率冲击能够显著促进劳动力投入变动程度。(5)~(8)列加入各自交互项后,我们采用极大似然估计方法来估计系数,可见交互项系数至少在10%显著水平上为负,说明随着生产率冲击逐渐增大,其对劳动力投入量变动程度的影响逐渐减弱,两者呈现非线性关系。
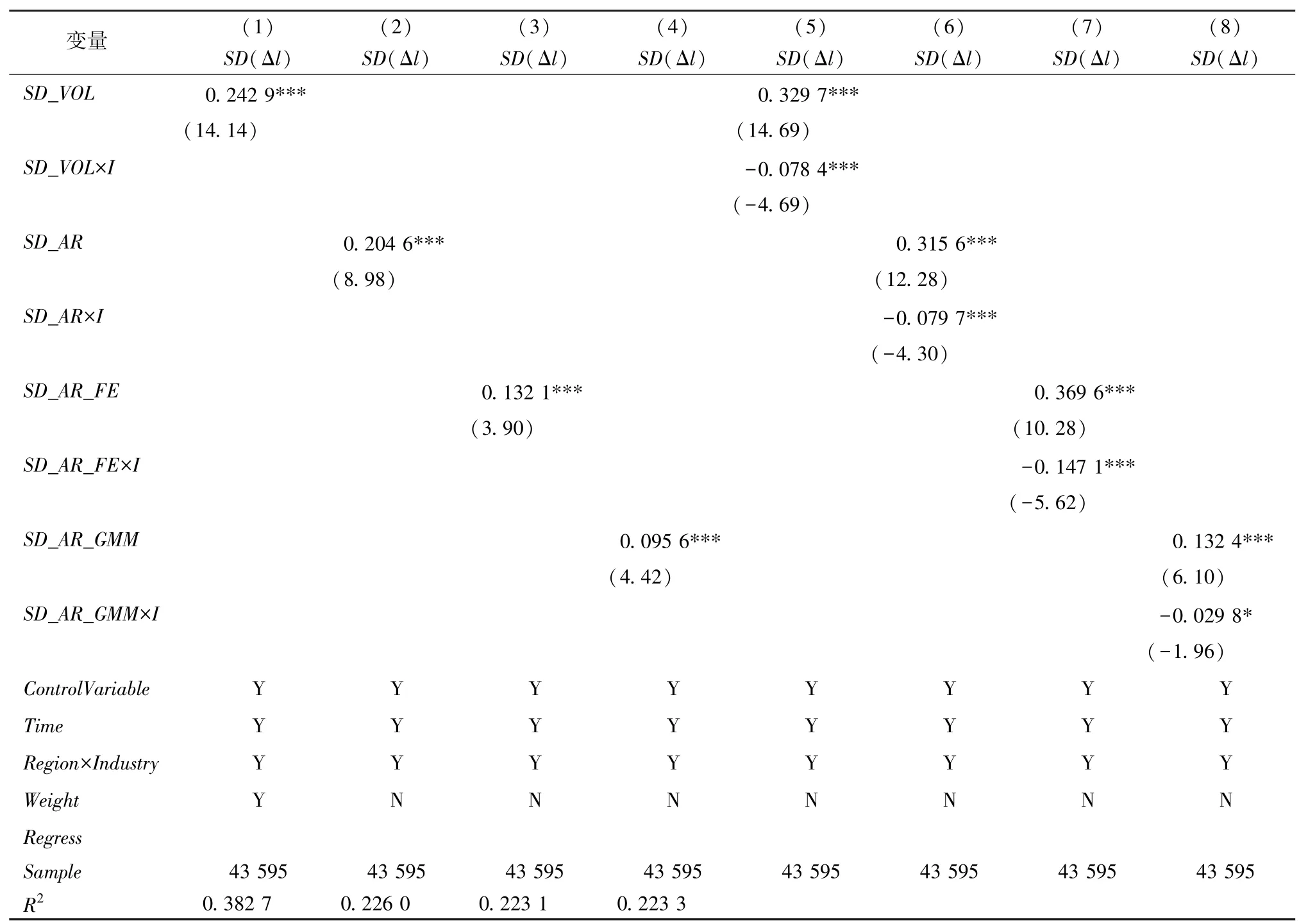
表3 劳动投入变动与生产率冲击关系
五、来自结构分析的证据
将企业按不同的所有制类型分为国有企业、集体企业、民营企业、外资企业、中国港澳台外资企业、混合所有制企业六种类型。采用动态分析模型及估计方法来估计出每种类型企业的调整成本参数。具体来说,使用离散状态空间方法来解出公式(7),其中:设置l(劳动力投入量的对数)的格点范围[3,10],每个单元格点为0.1;生产率格点数为30,并使用Tauchen[34]的方法计算转换矩阵;以最后一年的模拟数据计算劳动雇佣量比例超过20%的企业比例,并对所有年份劳动力变动及劳动边际产出数据求标准差。从而得到三个模拟目标矩的值,然后运用格点搜索法找到使得(8)式中Q(θ)最小时,所对应的待估计调整成本参数。
(一)基本估计结果
按照以上估计方法,得到调整成本参数估计及目标矩对比结果如表4 所示。根据表中对于实际矩的统计结果,可以看出劳动投入变化在各种类型企业间的差异。在国有企业和集体企业中,劳动雇佣量小规模变动(小于5%)的企业占比较多,但该比例在中国港澳台独资企业及外商独资企业中相对较小。而在中国港澳台独资企业、外商独资企业及民营企业中,劳动投入变动幅度较大(大于20%)的企业占比相对较多。一种可能的解释是,在我国,国有企业、集体企业承担着保就业的社会目标,维持就业量相对稳定是国有企业、集体企业的目标之一,因此在这两类企业中劳动投入呈现小规模变动的企业较多。对于追求利润最大化的外商独资企业(包括中国港澳台独资企业)、民营企业来说,根据生产率变动适时调整劳动投入才能使其达成目标。

表4 参数估计结果
另一方面,从调整成本系数估计的总体特征来看,所有企业的凸性调整成本系数均较大,但固定成本系数均较小①。这与本文的调整成本结构设计有关。(5)式中将固定成本系数表示为干扰成本的形式(即固定成本表示为利润占比),在这样的情况下,只有固定成本系数较小时才符合实际情况。从不同企业类型对比的结果看,外商独资企业及中国港澳台独资企业的凸性调整成本系数较高,但集体企业和民营企业该系数值较低。对于固定成本系数来说,外商独资企业该系数值较大,国有企业次之,集体企业和民营企业该系数值小于0.000 2。
(二)反事实模拟结果
为了考察不同反事实情况下,生产率冲击在调整成本作用下对企业影响的异质性,我们借鉴Asker et al.[4]的拟合优度指标,来衡量模型的拟合效果。


表5 反事实模拟结果
表5 第2 列给出了不同模型对总体经济的拟合程度,第3~8 列计算了相对于现实经济模型而言,在各种反事实模拟情景下,各类型企业人均产出的变动值。模型1 以现有各类型企业的实际参数(包括反映生产率冲击、生产技术、劳动边际产出、调整成本等参数)来模拟总体经济,其拟合优度值为0.107 4。模型2 将各类型企业的调整成本系数统一为总体系数的2 倍时,模型拟合度有所下降。并且由于调整成本上升,使得各类型企业的人均产出比现实经济均有所下降,横向对比发现,受影响较小的是国有和集体企业。在模型3 中用总体经济的调整成本系数替换各类型企业的各自系数后,发现总体拟合优度比现实经济模型有所提升,所有企业人均产出比现实经济均有所提升,其中中国港澳台、外商企业受益较多。模型4 使得各类型企业的调整成本系数均统一为总体系数的一半,此时所有企业的调整成本系数都有所下降,由于企业能够相对灵活地调整要素投入,使得模型模拟值与实际值差距缩小,将模型的拟合度提升到0.129 8。另外,调整成本的普遍下降,使得各类型企业的人均产出相对于现实经济均有所提升,提升效果较明显的仍然是中国港澳台独资企业和外商独资企业,并且受益程度大于模型3。从模型3、4 的对比结果也可以看出,当调整成本下降1 倍时,所有企业的人均产出上升了3~4 倍。模型5 是假设所有企业具有相同的生产技术,此时模型出现了过度拟合,但人均产出比现实经济大幅增加,说明消除不同企业间生产技术的差异对于提升产出效率具有重要作用。在模型6 中,把生产率冲击的持续性参数和波动性参数均下调为最小值②,此时模型拟合优度较现实经济模型提升了6 倍,可能的原因在于生产率冲击减弱,使得企业的要素投入相对稳定,模型拟合值与现实值差距较小,提升了模型的解释能力。另外,在生产率冲击减弱的情况下,所有企业的人均产出均有所提升。对比模型4 与模型6,两种措施均能提高企业的人均产出,但提升效果在不同类型企业间存在一定差异。对于中国港澳台和外商独资企业来说,降低调整成本能够带来较显著的政策效果,而减弱生产率冲击能使国有、集体、民营及混合制企业较多受益。
六、结论及启示
本文结合动静态分析方法,验证了生产率冲击、劳动力调整成本与劳动力资源配置的关系,考察了双重压力对我国企业劳动力资源配置造成的影响,并通过构建反事实,模拟了劳动力调整成本、生产率冲击等变动对不同类型企业劳动力资源配置的异质性影响,提出了差异化“减负增效”的策略。一方面,静态分析结果表明,由于存在劳动力调整成本,使得企业在进行动态劳动力配置时,不能根据生产率冲击来灵活调整劳动力投入,进而造成行业内企业间的劳动边际产出离散度增加,即出现了调整成本与生产率冲击双重压力下的劳动力资源储配。另一方面,结构估计的动态分析结果进一步从企业异质性角度说明了劳动力调整成本在劳动力资源配置中的作用。具体来说,我们发现凸性调整成本系数在不同类型企业间存在较大差异,但固定成本系数均较小。结合反事实模拟结果,可以看出中国港澳台和外商独资企业对劳动力调整成本较为敏感,而我国国内企业包括国有、集体、民营企业对生产率冲击反映较为强烈,降低调整成本和生产率冲击都能提高企业的人均产出水平,提升劳动力资源配置效率。从本文的研究中,可以得到的政策启示为:在我国企业遭受双重压力的情况下,通过为企业提供稳定的经营环境,减少生产率冲击,并降低企业在招聘、解聘中发生的行政、法律成本等劳动力调整成本的方式来为企业减负,能够弱化劳动力资源错配带来的不利影响。对不同企业,应采取适度的政策偏向,走差异化的“减负增效”之路,对于外商独资企业(包括中国港澳台独资)应更加注重降低其在劳动力雇佣或解聘时所发生的制度成本,使其能够灵活调整劳动力投入,提升劳动力资源配置能力。
注释:
①表4 中固定成本系数为0,并不代表固定成本不存在。本文选择格点的最小单位为0.000 2。
②根据实际数据计算所得,持续性参数最小值为0.107 4,波动性参数最小值为0.038 4。
