倍角坐标系下的随机高频信号注入解调策略

储剑波，朱叶，张开鑫

(1.南京航空航天大学 自动化学院，南京 211106；2.航空工业金城南京机电液压工程研究中心，南京 211106)

0 引 言

内置式永磁同步电机(interior permanent magnet synchronous motor, IPMSM)作为一种成熟的电机，具有高效率，高功率密度，稳定性好等优点，已经被广泛应用于需要高性能控制的领域中[1]。IPMSM在低速阶段常用的无位置方法为高频注入法[2]，根据注入类型分为旋转高频注入和脉振高频注入，以及方波信号注入[3]。由于需要额外注入高频信号，同时转子位置信号中夹杂直流分量，基频以及高频信号波，不可避免的会运用较多带通与低通滤波器，这将引入幅值误差以及相位偏移，造成软件延时，系统相对复杂等问题[4]。同时，高频注入的频率是固定的，这将在电流的功率谱中出现较大的谐波[5]，突出的外在表现是刺耳的噪声问题。

对于传统旋转高频电压法使用过多滤波器造成相位延迟、幅值衰减问题，文献[6]提出一种带宽可调节的滤波器，来代替原有固定频段滤波，增加了高频注入法的转速，但是系统过于复杂化，实际应用范围较窄。文献[7]提出一种对滤波器后的信号进行幅值和相位自适应的补偿策略，但是在低速阶段，算法无法准确获取补偿角度。文献[8]提出一种基于电流斜率变化率的解调方法，但是其采用的过采样将增加采样频率，对于硬件要求过高，且需要额外的PWM处理手段。文献[9]简化了信号处理过程，移除了低通滤波器的使用，从而使得系统具有不错的动态性能。

针对解决高频响应电流引起的噪声问题，文献[10]提出根据速度来降低注入幅值的方案，但是该方案会不可避免的增大解调过程中位置估计误差。文献[11]采用低频注入来降低人对频率的可听范围。但是该方案难以保证信噪比，增加了实现的复杂性。

文献[12-14]对传统旋转高频注入法进行了改进，但并没有一种方法能够很好的降低运算和系统复杂度，同时减少对滤波器的使用及高频注入下的噪声。因此，本文提出随机注入方案，将随机高频旋转电压注入估计坐标轴系，来获取IPMSM高频激励模型，以降低高频噪声的影响；同时，为了降低解调过程中滤波器的使用频率，推导了一种基于倍角坐标系的旋转高频信号注入法信号提取策略，来求取转子位置。利用MATLAB/Simulink建立相关模型，求取估计转子位置并对精度进行分析，最后通过实验来验证所提方法的正确性及动态性。

1 PMSM基本方程及高频激励方程

基于估计坐标轴注入旋转高频电压的无位置控制系统结构框图如图1，该系统采用id=0磁场定向控制策略。

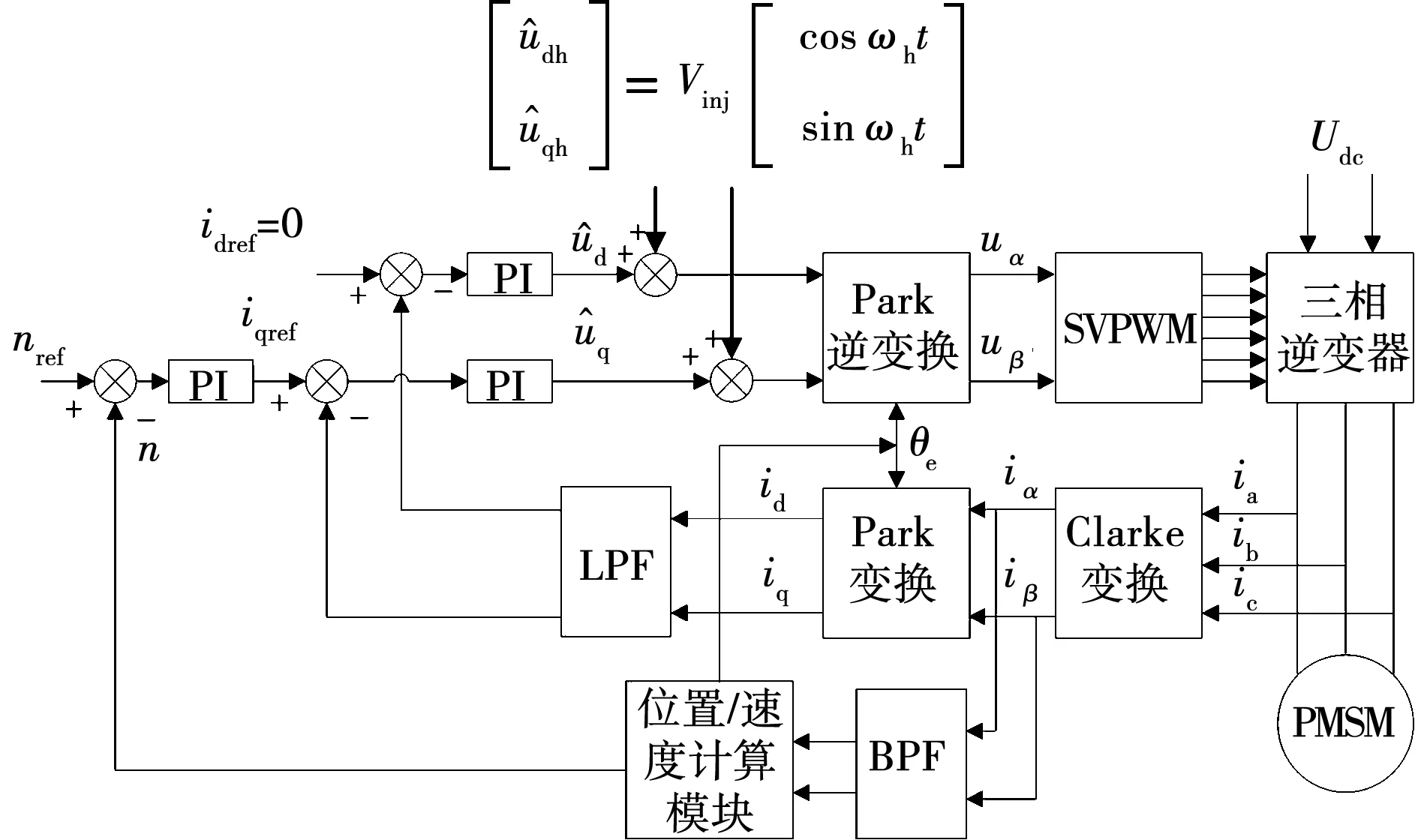
图1 基于旋转高频注入的PMSM无位置控制系统框图Fig.1 Block diagram of PMSM sensorless control system based on rotating high frequency injection

永磁同步电机基本电压方程为

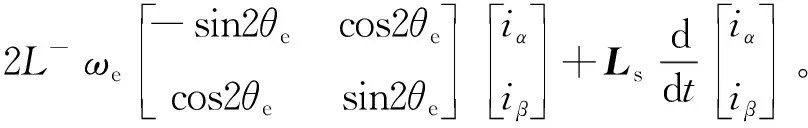
(1)

式中：uα、uβ为α-β轴定子电压；iα、iβ为α-β轴定子电流；Rs为定子绕组电阻；ωe为电角速度；λf为转子励磁磁链；Ls为电感矩阵，即

(2)

式中：L+=(Ld+Lq)/2,为均值电感；L-=(Ld-Lq)/2,为差值电感；Ld、Lq分别为电机d-q轴定子等效电感。

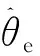
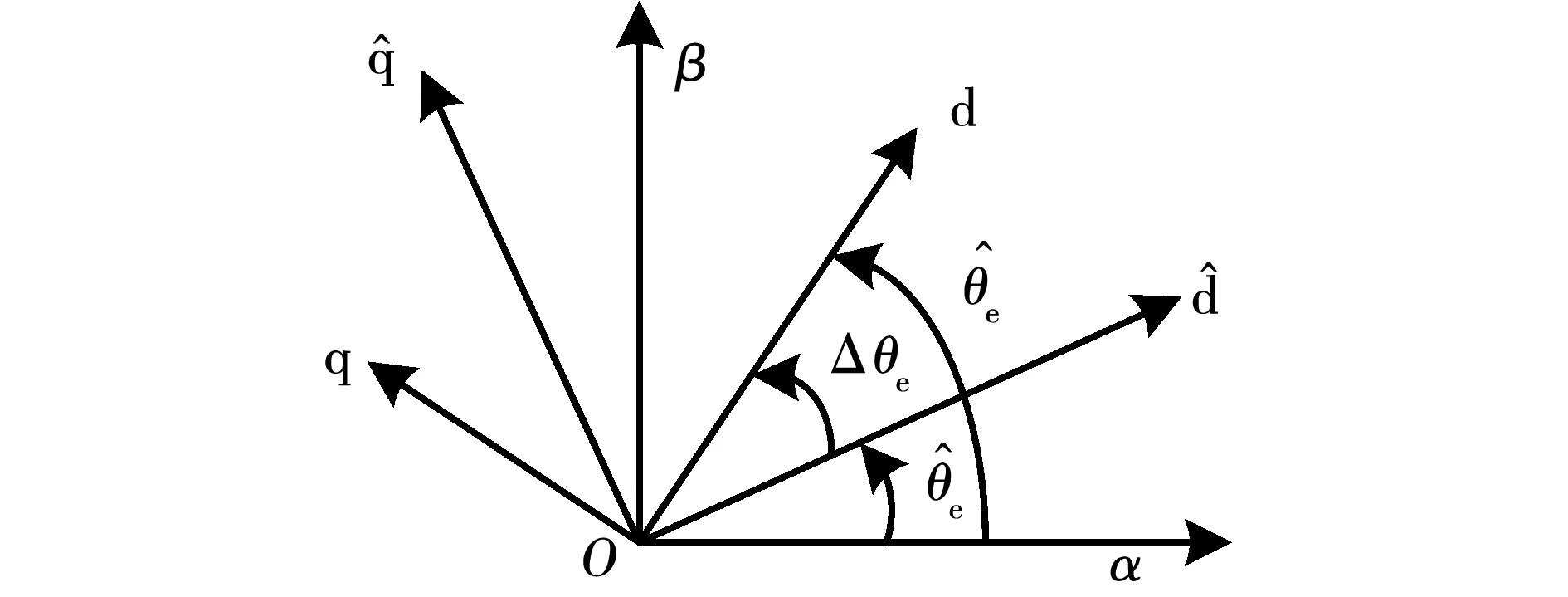
图2 实际与估计d-q坐标系统框图Fig.2 Block diagram of actual and estimated d-q coordinate system

(3)

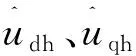
由于注入信号频率通常为几千赫兹，远远大于电机基波频率，可将永磁同步电机回路近似等效为RL回路，因此式(1)中定子电阻项远小于电抗项，可将其忽略。同时，由于研究的旋转高频注入法处于零低速阶段时反电动势极其微弱，也可以忽略不计。因此，结合上述分析，可将旋转高频注入下的电机激励模型简化为

(4)

其中iαh、iβh、uαh、uβh分别为高频信号注入下电机在静止坐标系上的高频响应电流和电压。

此时，静止坐标轴下的高频响应电流可以由下式求出：

(5)

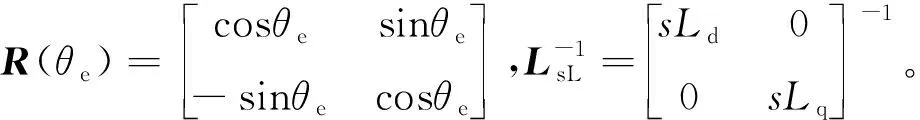
由式(5)知，高频注入信号将结合电机凸极性形成电机高频响应信号，响应信号中包含转子位置，适当解耦可有效追踪电机转子位置。

2 双频随机注入及无位置解调策略

传统高频注入法由于固定高频的存在，使定子绕组产生高频振动并转化成高频噪声，这不仅限制电机应用的场景，且带来的电磁兼容问题也将对设备进行干扰。为有效抑制干扰源，从噪声源上研究噪声的产生是最直接有效的方法[15]。近年来，将频率随机化作为降低噪声的一种策略逐渐被应用于高频注入中[16]。其中，双频随机信号注入能够降低注入频率及倍频在电流频谱中的能量峰值，从而使得功率谱密度中离散谱与连续谱平缓过渡，达到抑制噪声的效果[17-19]。

2.1 双频随机高频信号的产生与注入

为了解决单一高频注入所带来的噪声问题，将采取双频随机高频注入来降低因高频注入引起的电流功率谱密度中的噪声幅值。选取频率不同的两个信号作为基本注入信号。其信号注入方式如图3所示。注入频率表示为

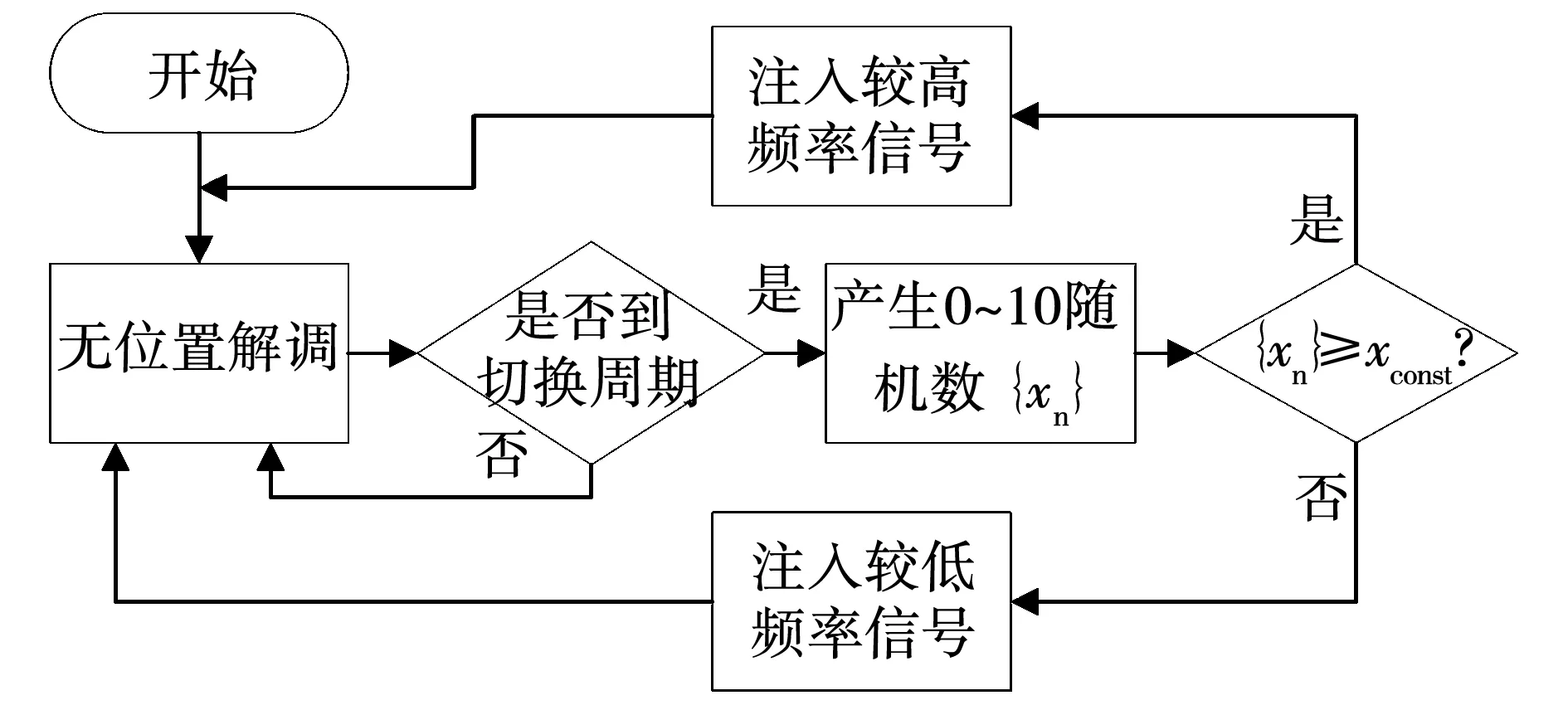
图3 随机注入流程图Fig.3 Random injection flow diagram

(6)

式中：f1为较高注入频率；f2为较低注入频率；且f1>f2，xconst为随机切换阈值。对于两种频率注入信号，阈值xconst大小决定切换周期，可用来调整高低频率注入概率，最大限度的达到抑制电流谱密度波形中离散谱的目的。

该随机注入的主要过程可以描述为：当电机进行到新的注入周期时，先由随机数模块产生一个0～10的随机数xn，再与设定的切换值xconst比较来决定该周期注入较高频率还是较低频率。再进行无位置计算，在下一个新的注入周期时重复上述操作。

将旋转高频电压信号注入d-q坐标系，是基于内置式电机的高频注入法中注入信号与坐标系的不同结合，方式新颖但解调策略较为单一，其实现技术及优势缺乏必要的研究和讨论。因此提出一种基于倍角坐标系的转子位置解调新方法，采取高频激励电压与电流模型，从基本坐标系的变换中来提取转子位置。

2.2 倍角坐标系的建立与解调策略分析

为方便分析，通过将α和β轴逆时针旋转2θe来建立新的测量旋转坐标系，记为γ-δ坐标系，其中γ轴超前同步旋转坐标轴d轴θe度，δ轴超前同步旋转坐标轴q轴θe度，如图4所示。

图4 γ-δ 坐标轴系示意图Fig.4 Schematic diagram of γ-δ axes

假设γ-δ轴高频响应电流为iγh、iδh，结合iαh、iβh，由Park变换知，两者关系可以表示为

(7)

对于旋转高频电压注入引起的α-β轴高频响应电流iαh、iβh，会在γ-δ轴得到高频响应电流iγh、iδh。将iγh、iδh进行Park逆变换，得到同步旋转d-q轴响应电流，同时将iαh、iβh进行Park变换，也得到同步旋转d-q轴响应电流。理想情况下，变换后的电流相等，得到

(8)

经过适当变换后可以得到：

(9)

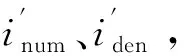
通过对高频激励电压方程(4)进行积分和微分变换并展开，并结合式(7)，可得出

(10)

故可以通过对高频电压积分，结合高频电流计算来计算高频注入电压在倍角坐标系下的高频电流响应，即

(11)

计算出高频响应电流后，可代入式(9)直接求出转子位置。整个无位置策略的结构框图如图5所示。主要包含两个步骤：首先结合传统坐标系对倍角坐标系下高频激励信号进行分析与求取，得到包含转子位置信号的混合信号；然后，对混合信号进行适当数学计算，去除混合信号中高频耦合项对解调的影响，从而准确提取转子位置信息。

图5 基于倍角坐标系解调结构框图Fig.5 Demodulation structure block diagram based on double angle coordinate system

考虑到式(9)在角度计算过程中引入除法，且分子分母均包含高频信号，而解调出的角度为基频，在计算过程中可能引入高频过零点。在MATLAB中对该方案进行仿真得到角度波形如图6，结果表明在该计算方式下角度解调将产生较多高频毛刺，需要对其信号处理形式进行进一步的分析与改进。

图6 解调过程中的高频毛刺Fig.6 High-frequency burr during the demodulation

对式(9)中分子分母的组成形式进行求解，得到：

(12)

(13)

由式(12)知，该位置解调策略下的信号是由基波和高频信号波组成的混合信号，且混合信号中基频和高频以乘积形式表示。因此提取的角度信号容易产生大量正负不定的高频毛刺，导致了提取转子位置信号正余弦信号的波动，需要去除高频耦合信号对解调带来的影响。

2.3 滤除高频分量的转子位置提取方法

通过对注入高频电压信号进行Park变换，可以得到同步旋转d-q轴系下的高频电压为

(14)

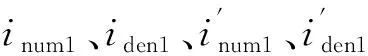
(15)

(16)

(17)

如果直接利用除法来消除高频含量，则不可避免的引入过零点。因此利用简单三角函数计算来避免高频项参与除法运算，实现对角度正余弦信号的提取。其计算结构框图如图7，该方法仅对计算变量进行简单相乘与相加，便可实现角度正余弦信息解耦，计算过程为：

图7 位置信号提取结构框图Fig.7 Position signal extraction structure block diagram

cosθecos2(ωht-Δθe)+

cosθesin2(ωht-Δθe)=cosθe；

(18)

sinθecos2(ωht-Δθe)+

sinθesin2(ωht-Δθe)=sinθe。

(19)

由提取过程可知，在不对高频进行除法运算的前提下对基频转子位置信息进行有效提取，避免了高频过零点对解调的影响，最终转子角度可以经反正切求出。较式(9)相比，改进后的方法既没有过高的运算复杂度，又没有对系统进行高采样频率要求，同时能够降低传统解调方法中对低通滤波器的使用，从而减小解调时的幅值衰减与相位延迟问题，提高系统动态性能及稳定性。

3 仿真与实验验证

3.1 仿真验证

为了验证该方法的正确性及在PMSM无位置传感器控制技术中的估计性能，在MATLAB/Simulink中对该方法进行模型搭建并仿真研究，仿真中的电机额定转速为18 000 r/min，额定转矩为0.45 N·m，极对数为2。随机注入高频电压信号幅值分别为2 V和2.5 V，频率分别为0.8 kHz和1 kHz。

为验证该无位置算法低速性能，给定转速100 r/min，并空载启动，在4 s时突加负载，7 s时突卸负载，观察相关波形，如图8所示。

其中，图8(a)表示估计转速与实际转速波形对比。可以看出新解调策略能够准确跟踪转速信息，且具有一定的抗负载扰动能力。

图8(b)、(c)分别表示估计角度与实际角度波形对比及其局部放大波形，图8(d)为运行时角度误差波形，从图中误差变化知，在速度上升阶段存在一定的角度误差，稳态时误差缩小，经过适当角度补偿后，估计角度与实际角度波形重合，对于突加突卸负载，角度误差也能很快收敛至0。

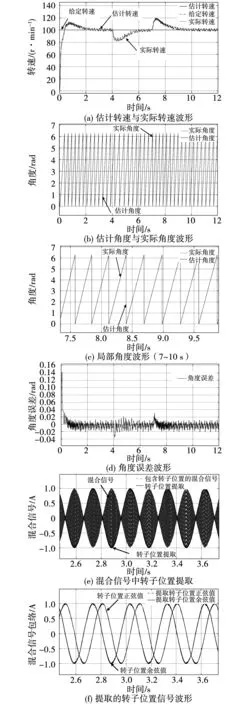
图8 无位置方法仿真波形Fig.8 Sensorless method simulation waveform

图8(e)、(f)表示对混合信号中inum1、iden1转子位置提取及包络线反应的转子位置正余弦信息，可知所提出的新解调策略可以良好的对转子位置信息进行提取，估计角度恰为该混合信号的包络，且提取精度很高。

接下来对随机频率注入下电机低速运行性能进行仿真，给定转速100 r/min，启动负载为0.11 N·m，在4 s时使电机升速至300 r/min，稳态后再将负载逐渐升至0.23 N·m，运行结果如图9所示。结果显示，新解调策略能够有效应对低速下转速突加突降变化，转子位置提取良好，动态响应能力较好且转速误差较低。

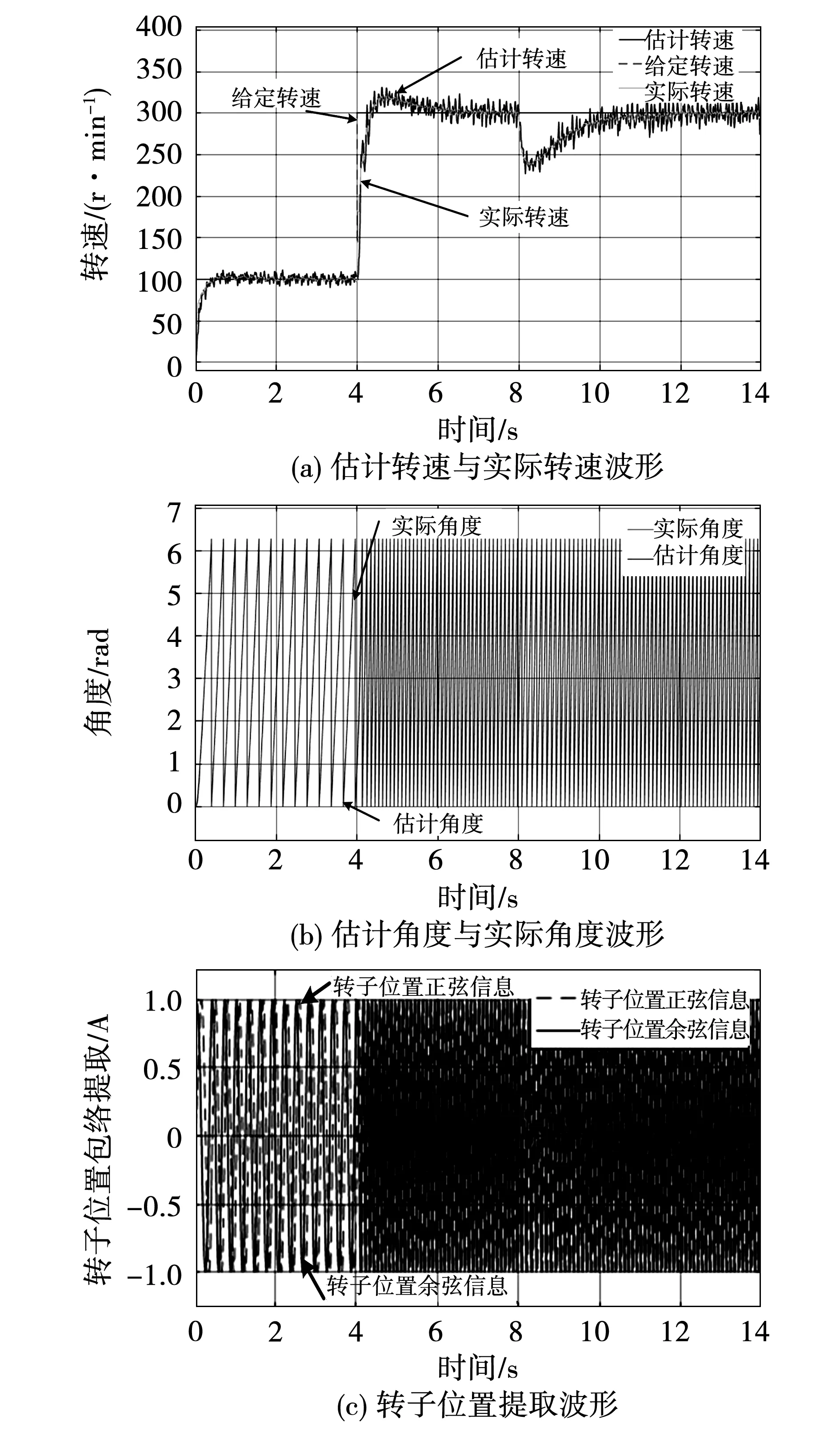
图9 随机注入下转速及负载突变仿真波形Fig.9 Simulation waveforms of speed and load sudden changes under random injection

对随机频率注入下电流功率谱密度进行仿真分析。对固定频率800、1 000 Hz及混合频率注入下A相电流进行功率谱分析，得到图10所示波形。

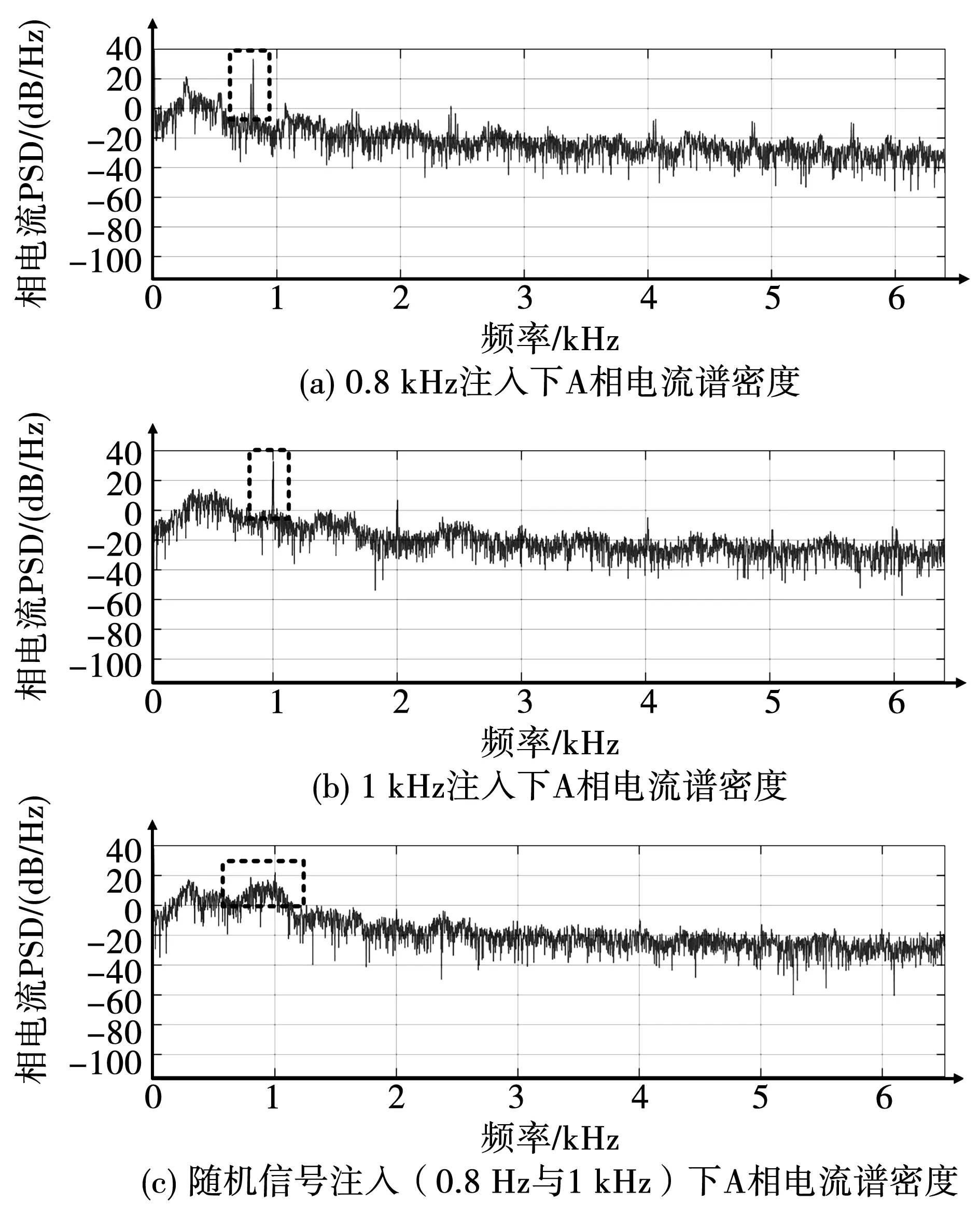
图10 不同频率注入下功率谱密度分析Fig.10 Analysis of power spectral density under different frequency injection

波形图表明，采用随机频率注入可以削弱功率谱密度尖峰能量，使该处能量平滑延展，进而降低噪声的刺耳性，以达到降低噪声的目的。

3.2 实验验证

为了进一步验证该方案在实际工程领域的效果，在以MC56F82743为核心的500 W内置式永磁同步电机实验平台上开展相关实验。实验平台如图11所示，相关电机参数与仿真参数一致，PWM载波频率为16 kHz。相关波形由上位机软件FREEMASTER及示波器给出。

图11 实验平台Fig.11 Experiment platform

首先验证基于倍角坐标系的解调方法的低速效果，给定电机转速100 r/min并带载启动，观察无位置解调结果波形，如图12所示。结果显示所提出的无位置算法性能较好，误差较低，可以有效解调出转子位置信息。

图12 无位置方法实验波形Fig.12 Sensorless method experiment waveform

在200 r/min下进一步观察包含转子位置的混合信号inum1、iden1波形，如图13所示。可以看出，解调过程中提取的包络线较为良好的反应了转子角度正余弦信息，且经过归一化后可以避免混合信号幅值波动带来的影响。

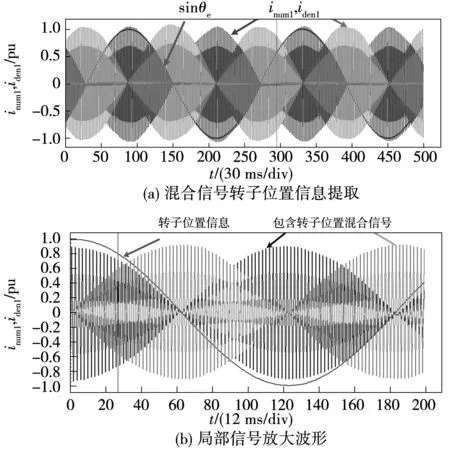
图13 混合信号与信号包络Fig.13 Mixed signal and signal envelope

再检测随机高频注入下的电机稳定性。随机注入信号如图14所示。可以看出，切换的时刻为两种注入高频信号的整数倍。恒定的压频比也能保证切换时不会产生较大的转速误差。切换时的转速波动见图15所示。切换前后转速过渡较平稳，且转速误差基本很小，能够良好适应该无位置算法。

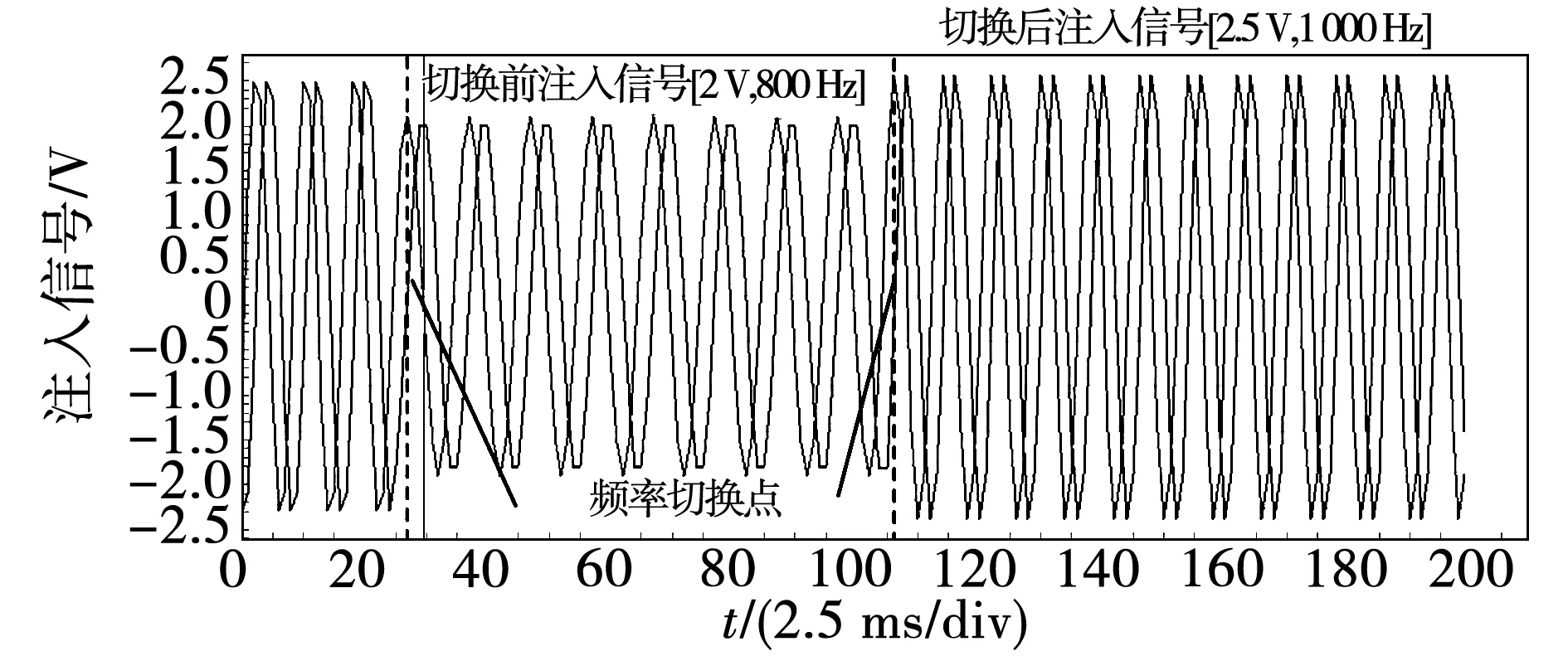
图14 随机注入信号Fig.14 Random injection signal

图15 频率切换前后转速波动Fig.15 Speed fluctuation before and after frequency switching

根据分析，随机频率注入可以降低电流谱中高频谐波尖峰。要观察随机注入信号对噪声的影响，分别对单一频率及随机频率注入进行实验，对相电流波形采集并进行功率谱密度分析。相关波形如图16所示。

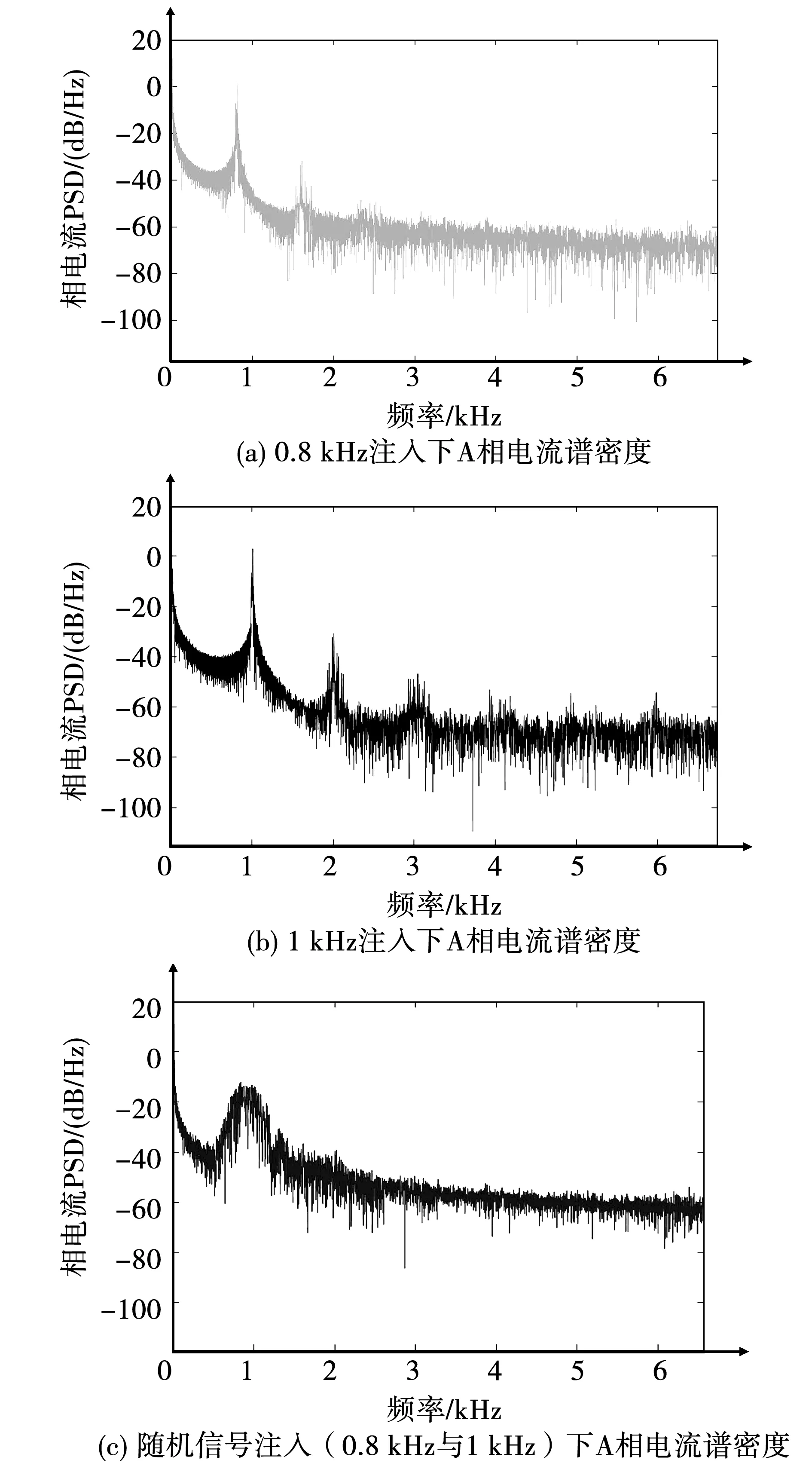
图16 功率谱密度分析Fig.16 Power spectral density analysis

在单一高频信号注入下，电流谱密度中注入频率产生的能量较大，而随机信号注入能够对高频峰值进行削弱，使得高频能量分布较为均匀。从而达到降低噪声的效果。

对电机低速带载运行下转速突变的动态性进行实验验证。电机带载启动至70 r/min，然后依次给定30、40 r/min的阶跃，得到转速变化为70-100-140 r/min的A相电流波形如图17所示。由图可知，在速度突变时，该无位置方法能够进行快速准确跟踪，且具有良好的动态性。

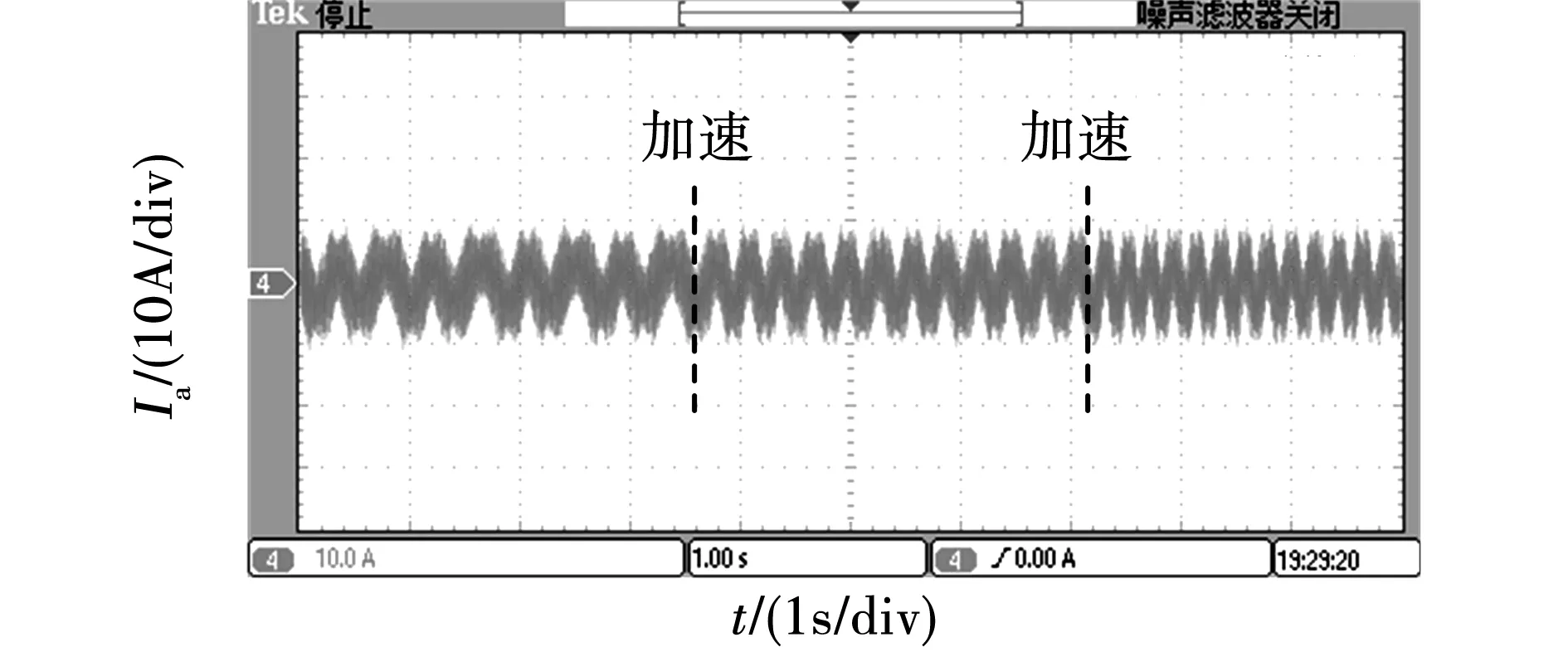
图17 转速突变时A相电流波形Fig.17 Phase A current waveform when the speed changes suddenly

考虑到实际工程应用中的带载问题，对电机的低速加载能力进行实验测试。给定电机转速200 r/min，同时给定突加负载及突卸负载变化。相关波形如图18(a)、(b)所示。结合上图实验结果表明，该无位置方法能够有效适应低速下转速及负载变化，提高系统可靠性。

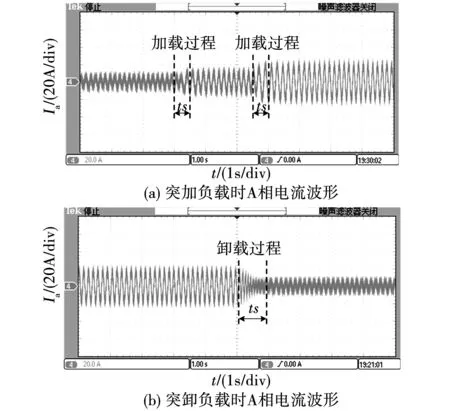
图18 带载实验A相电流波形Fig.18 Phase A current waveform during load experiment

4 结 论

本文主要对随机高频信号注入在内置式永磁同步电机中的解调策略进行研究，总结如下：

1)采用旋转高频电压注入到同步旋转估计坐标系的无位置传感器控制系统结构相对简单；利用永磁同步电机凸级效应及高频激励响应来计算位置信息，可以实时准确实现位置观测。

2)通过倍角坐标系对高频响应电流进行提取，经简单数学计算简化位置信号公式表达形式，使用转子位置提取模块提取转子位置的正余弦信号，有效避免了高频项对解调的耦合效果。相较于以往的带通加低通滤波器调制的信号提取方案，去除了低通滤波器的设计过程，从而避免了低通滤波器引入的延时、相位偏移及幅值损耗等问题，且不需要引入额外的解调信号，避免了调节的复杂性，简化了调节过程，有效增加了信号提取的快速性和准确性。

3)针对高频注入引起的噪声，选取两种频率并引入随机数对其进行随机交替注入，来削弱电流谱中高频谐波的峰值。对电流的功率谱密度进行分析，可知该方法能够有效的对高频进行抑制，且能够降低可听噪声。

对基于倍角坐标系的高频信号注入法信号提取策略进行实验分析，证实了该方案的可行性及有效性。