基于增强深度自编码网络的滚动轴承故障诊断方法
2021-11-18童靳于郑近德
童靳于 罗 金 郑近德
安徽工业大学机械工程学院,马鞍山,243032
0 引言
滚动轴承作为旋转机械中的关键传动零部件,面对复杂多变的工业设备运行工况,不可避免地会出现各种故障,因此,滚动轴承状态监测和早期故障诊断具有重要的现实意义[1]。
特征提取是滚动轴承故障诊断的关键步骤[2]。通过轴承振动信号的分析与处理,提取能够反映故障信息的时域、频域和时频域特征[3-5],将所提特征输入分类器中进行模式识别,可以判断设备的故障类型。常用的分类器有基于传统机器学习的随机森林(random forest,RF)[6]、支持向量机(support vector machine,SVM)[7]和人工神经网络(artificial neural network,ANN)[8]等。这类传统机器学习算法的浅层结构缺乏强大的特征表示能力,它获得良好精度的前提是依据先验知识提取反映故障类型的敏感特征。然而,特征提取容易造成关键信息丢失,从而导致异常事件预测准确率下降。同时,浅层机器学习无法完成工业大数据的诊断问题。
近年来随着先进传感技术、大数据技术的发展及其在工业领域的应用,深度学习的发展为机械设备故障诊断提供了新的研究思路和方法。深度学习通过构建深层次的非线性网络,可以自动挖掘隐藏在原始数据中的代表信息,并建立振动数据和设备的运行状态之间的精确映射关系[9]。常用的深度学习模型有深度置信网络(deep belief network,DBN)、卷积神经网络(convolutional neural network,CNN)和深度自编码网络(deep auto-encoder network,DAEN)等。其中,DAEN因其能够自动从样本中学习到表征状态特性的特点而被广泛应用于设备故障诊断领域。文献[10]搭建了一种基于自编码器(auto-encoder,AE)的深度神经网络,并将其应用于轴承故障诊断。文献[11]提出了一种基于自编码器的深度特征融合方法,在轴承故障和齿轮故障实验分析中取得了令人满意的诊断结果。文献[12]成功地将基于稀疏自编码器(SAE)的深度神经网络用于感应电动机的故障分类。文献[13]提出了一种基于收缩自编码器(CAE)的旋转机械故障诊断方法。然而,当振动信号中包含较大噪声或奇异值时,上述方法诊断准确率大幅下降[14]。此外,DAEN超参数的选择一直依赖经验选取,选取结果对故障识别精度影响较大。
基于此,为了提高DAEN的特征挖掘能力,同时自适应地选取网络超参数,本文提出一种增强深度自编码网络,并将其应用于滚动轴承故障诊断中。
1 自编码器理论基础
AE是一个三层的无监督学习神经网络,三层分别为表示输入的输入层、表示学习特征的隐藏层和表示重构的输出层。输入层和隐藏层构成编码网络,将原始输入转换为隐藏特征。隐藏层和输出层构成解码网络,将隐藏特征重构为与原始输入相同维度的输出表征[15]。AE的结构如图1所示。
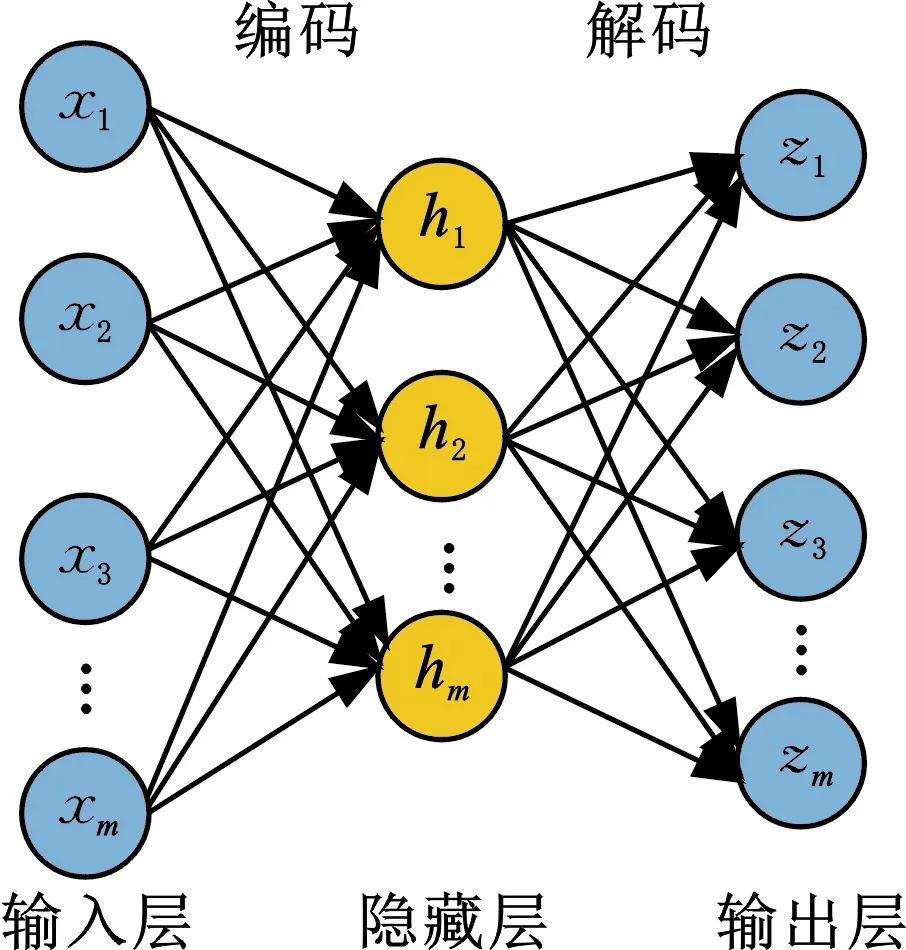
图1 AE的结构图Fig.1 The structure of AE
假设输入样本集为x=(x1,x2,…,xi,…,xm),编码网络可以表示为
h=s(Wx+b)
(1)
解码网络可以表示为
z=s(W′h+b′)
(2)
式中,W、W′分别为编码网络和解码网络的权重矩阵;b、b′分别为编码网络和解码网络的偏置矩阵;s为激活函数;h为隐藏层特征;z为输出层特征。
均方误差(mean squared error,MSE)通常用作AE的损失函数,定义如下:
(3)
式中,‖·‖表示范数。
这样,m个样本的总损失函数为
(4)
2 增强深度自编码网络
当设备工况变化,振动信号中包含大量噪声和奇异值时,DAEN的特征提取能力显著下降。鉴于此,本文提出了一种增强深度自编码网络以提高DAEN在变工况条件下的特征提取能力。
2.1 网络的构建
最大相关熵是一种非线性和局部相似度量函数,对复杂信号特别是包含非平稳背景噪声的轴承振动信号不敏感,可以很好地用来提取信号的潜在特征[16]。本文采用最大相关熵代替MSE作为AE的损失函数。
样本集A=(a1,a2,…,ai,…,an)和B=(b1,b2,…,bi,…,bn)间的相关熵定义为
(5)
式中,E(·)为期望值;kσ(·)为核函数;FAB(·)为联合密度函数。
在实际工程应用中,联合密度函数经常是未知的,可以用一组样本估计两者间的相关熵,表示为
(6)
式中,m代表样本数。
高斯核通常被用做相关熵的核函数[17],其定义如下:
(7)
那么,AE的损失函数可定义为
(8)
一般地,可以通过在AE的损失函数中引入正则化项以避免过拟合并学习更加鲁棒的特征表示[18]。稀疏惩罚作为一种常见的正则项约束,将其添加到AE的损失函数中,可以有效地降低输入数据的维数,加快网络训练的速度[19]。收缩惩罚项可以从噪声环境中学习具有代表性和鲁棒性的隐藏特征[20]。为了能够进一步挖掘更深层次、更具代表性的特征,综合考虑这两种正则项约束的优势,将稀疏惩罚项与收缩惩罚项同时作用于AE的损失函数,此时,AE的损失函数可进一步表示为
(9)

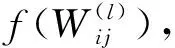
(10)
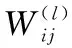
m个样本的AE总损失函数可表示为
(11)
式中等号右边第一项为新的重构误差;第二项为嵌入非负约束因子的收缩惩罚项;第三项为稀疏惩罚项。
被称为内存储器,计算机中所有程序的运行都是在内存中进行的,是用于暂时存放CPU中的运算数据,以及与硬盘等外部存储器交换的数据。
增强深度自编码网络通过堆叠多个AE以及一个softmax分类层而组成,其结构如图2所示。

图2 网络结构图Fig.2 The architecture of the network
2.2 网络训练方法
在网络训练时,首先将第一个AE的隐藏层特征h1作为第二个AE的输入,编码得到第二个AE的隐藏层特征h2,重复该过程直至完成所有隐藏层的预训练,再使用反向传播算法对网络进行微调,进一步优化网络所有权重,然后将最后一个AE的隐藏层特征hn作为softmax分类器的输入,得到分类识别率。
深度神经网络模型中通常有许多超参数,若训练样本不足则很容易发生过拟合,这时模型在训练集上表现良好,但是在测试集上表现一般,模型泛化能力较差。在网络训练阶段,dropout通过对隐藏层的神经元随机置零,使上一层神经元和网络随机挑选的下一层神经元共同工作,减弱神经元节点间的联合适应性,这样不仅能够提高测试集识别的准确率,而且可以达到缩短训练时间的目的。
2.3 网络参数自适应选择方法
影响增强深度自编码网络性能的关键参数分别为稀疏参数ρ、稀疏惩罚系数β、收缩惩罚系数λ和高斯核大小σ,手动调参很难保证设定的参数最佳且工作量很大。MIRJALILI等[22]于2014年提出了灰狼优化(grey wolf optimization,GWO)算法,因其所需设置的参数较少,同时收敛速度快,被广泛应用于参数自适应优化问题中。
本文利用GWO算法解决增强深度自编码网络中关键参数难以选取的问题。首先设置GWO算法的基本参数,包括狼群数量,迭代次数和参数寻优界限,其次将狼群位置依次赋给增强深度自编码网络的关键参数ρ、β、λ、σ,以关键参数的组合(ρ,β,λ,σ)作为GWO算法的最优解,最后以分类识别率作为GWO算法的适应度函数开始寻优,输出最优参数集(ρbest、βbest、λbest、σbest)。
2.4 诊断流程
基于所建立的增强深度自编码网络模型提出的滚动轴承故障诊断方法的诊断流程如图3所示。具体步骤如下:
(1)获取轴承振动原始信号,将其按一定比例分为训练集和测试集;

图3 诊断流程图Fig.3 The flowchart of the diagnosis
(2)设置GWO算法的基本参数,包括狼群数量、迭代次数、参数寻优上界与下界;
(3)初始化网络的参数,包括网络深度、输入维数、初始网络权重等,将狼群位置依次赋给增强深度自编码网络的关键参数ρ、β、λ、σ,开始训练;
(4)以训练集分类识别率作为GWO算法的适应度函数,训练网络;
(5)利用测试集验证训练完成的网络模型,并输出诊断结果。
3 实验验证
3.1 实验一
将本文方法应用于滚动轴承实验数据分析,实验数据来自美国凯斯西储大学的滚动轴承试验测试数据[23]。深沟球轴承的型号为SKF 6205-2RSJEM,通过电火花加工技术设置单点故障,在负载2.205 kW、转速1730 r/min、采样频率为12 kHz的工况条件下,采集具有局部点蚀的内圈故障、滚动体故障、外圈故障以及正常状态的滚动轴承振动信号。
每种故障类型取300个样本,每个样本包含400个连续采样点。对于每种故障类型的样本,随机抽取270个作为训练样本,剩余的30个作为测试样本。训练集共有1890个样本,测试集共有270个样本。实验一数据集如表1所示。
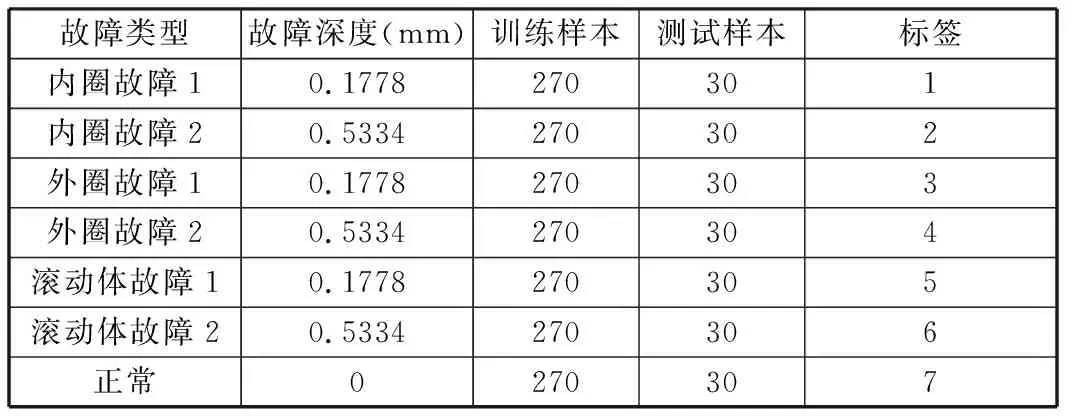
表1 实验一数据集信息Tab.1 The data set information of experiment 1
将本文方法与传统机器学习模型SVM、BPNN和三种深度自编码网络,即DAEN、深度稀疏自编码网络(DSAE)、深度收缩自编码网络(DCAE)进行比较。模型输入均为未经处理的原始时域信号。SVM的核函数采用RBF函数,惩罚因子与核函数参数分别设为(50,0.1);BPNN的网络结构设为[400 100 7],迭代次数200,学习率0.1。四种深度自编码网络结构均设置为[400 200 100 50 7],隐藏层数均设置为3层,迭代次数均为400次,激活函数均选择ReLU函数。通过GWO优化算法获得的一组最优参数(ρbest、βbest、λbest、σbest)为(0.07,0.25,0.05,13)。
不同方法的诊断结果对比如图4和表2所示。由此可以看出,传统的机器学习算法SVM和BPNN的10次试验平均准确率仅达到63.43%和59.52%。在四种深度自编码网络中,DAEN的测试准确率最低,10次试验平均准确率为91.52%,标准差为0.74;DSAE和DCAE的平均准确率分别为92.52%和93.33%,标准差分别为2.22和1.45,由此可以看出,DSAE和DCAE的10次试验准确率波动较大,表现不稳定;本文方法在10次试验中均取得了最高的测试准确率,平均准确率为95.95%,标准差为0.98。由此可以看出,与传统机器学习算法相比,深度自编码网络能够更好地挖掘轴承信号中的故障特征,建立轴承原始输入数据与故障类别间的对应关系;与未加入正则项约束的深度自编码网络(DAEN)相比,对自编码器进行正则化项约束能够有效提升重构性能;在三种加入正则项约束的深度自编码网络(DSAE、DCAE和本文方法)中,将最大相关熵函数作为自编码器的损失函数,同时在网络权重中嵌入非负约束后,能够较好地减少重构误差,在一定程度上提高了自编码器的特征提取能力和故障识别稳定性,同时,网络训练时加入dropout,可以有效提高测试集准确率。

图4 不同方法10次试验对比图Fig.4 Diagnosis results of 10 trials using different methods

表2 不同方法的诊断平均准确率及标准差Tab.2 The average diagnostic accuracy and standard deviation of different methods
图5为10次试验中本文方法第10次试验的混淆矩阵图。对角线上的数字表示本文方法对每类工况样本的识别率。从图中可以看出,本文方法仅在轴承故障类型为1和3时出现了误判,识别率分别为93%和90%,对其他类别轴承故障类型识别率均达到100%。

图5 本文方法第10次试验的混淆矩阵图Fig.5 Confusion matrix of the proposed method in the 10th trial
为进一步体现本文方法对原始信号的特征提取能力,通过t-SNE方法分别对原始数据和本文方法最后一个隐藏层特征进行降维可视化,原始数据和本文方法特征可视化分别如图6、图7所示,图中3个方向的坐标分别代表t-SNE方法分解的3个方向分量。
从图6和图7中可以看出,原始时域信号的聚类效果很差,每种故障类别的特征难以分辨。而本文方法提取的特征很容易区分,表现为相同故障类别的特征按照同一个中心聚集、不同故障类别的特征相距较远,表明了本文方法能够取得较好诊断结果的原因。

图6 原始数据特征可视化(实验一)Fig.6 Feature visualization map of raw data(experiment 1)
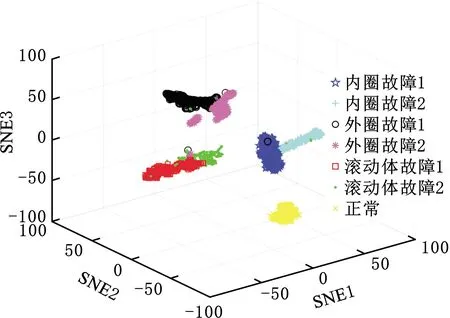
图7 本文方法特征可视化(实验一)Fig.7 Feature visualization map of the proposed method(experiment 1)
3.2 实验二
为了说明本文方法对变工况数据的故障诊断能力,选取同一实验台不同负载工况下的实验数据加以验证。实验数据取自安徽工业大学自制轴承实验台(图8)。实验轴承型号为SKF6206-2RS1,采用电火花加工技术分别对轴承内圈、外圈和滚动体加工出不同深度的故障,故障类型如表3所示。在不同负载、不同转速下采集了多种轴承运行状态的振动信号。

图8 自制实验台示意图Fig.8 The diagram of self-made experiment test rig
选取转速为1500 r/min、采样频率为10.24 kHz、负载分别为5 kN和7 kN工况下的轴承振动数据,两种工况共包含8种不同故障类型和损伤程度的数据,数据采集信息见表3,时域波形图见图9。每种故障类型取500个样本,每个样本包含400个连续数据点。对每种故障类型随机抽取450个作为训练样本,剩余的50个作为测试样本。这样,训练集共有3600个样本,测试集共有400个样本。
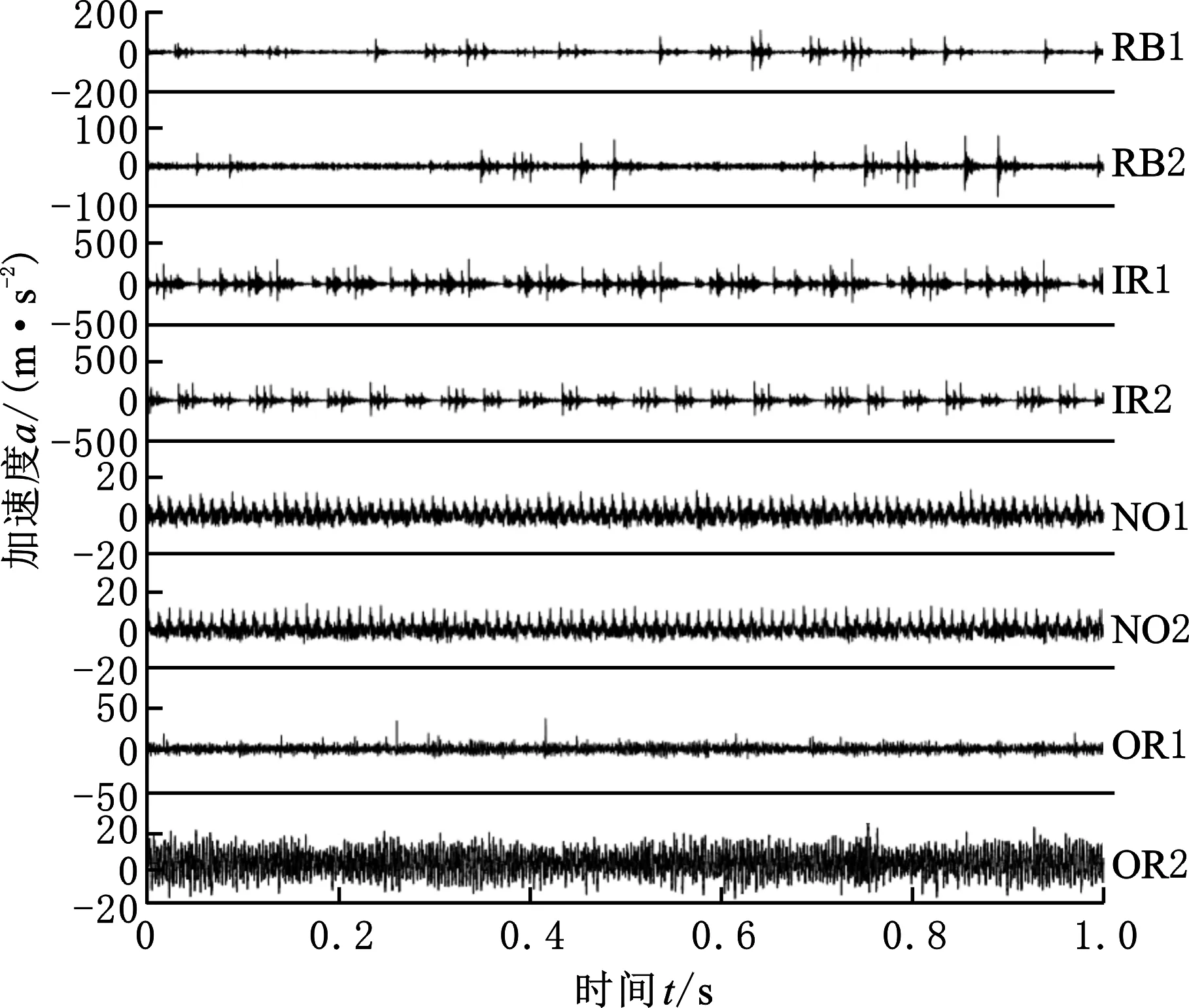
图9 故障数据振动信号Fig.9 Vibration signals of fault data
与实验一相同,将本文方法分别与SVM、BPNN、DSAE、DCAE和DAEN对比。SVM的核函数采用RBF函数,惩罚因子与核函数参数分别设为(50,0.1);BPNN的网络结构设为[400 100 8],迭代次数为200,学习率为0.1。四种深度自编码器网络结构均设置为[400 200 100 50 8],隐藏层数均设置为3层,迭代次数均为400次,激活函数均选择ReLU函数,学习率为0.01,通过GWO优化算法获得的一组最优参数(ρbest、βbest、λbest、σbest)为(0.01,0.13,0.46,13)。不失一般性地,取10次试验的平均准确率作为不同方法的性能评估指标。不同方法的诊断结果对比如图10和表4所示。
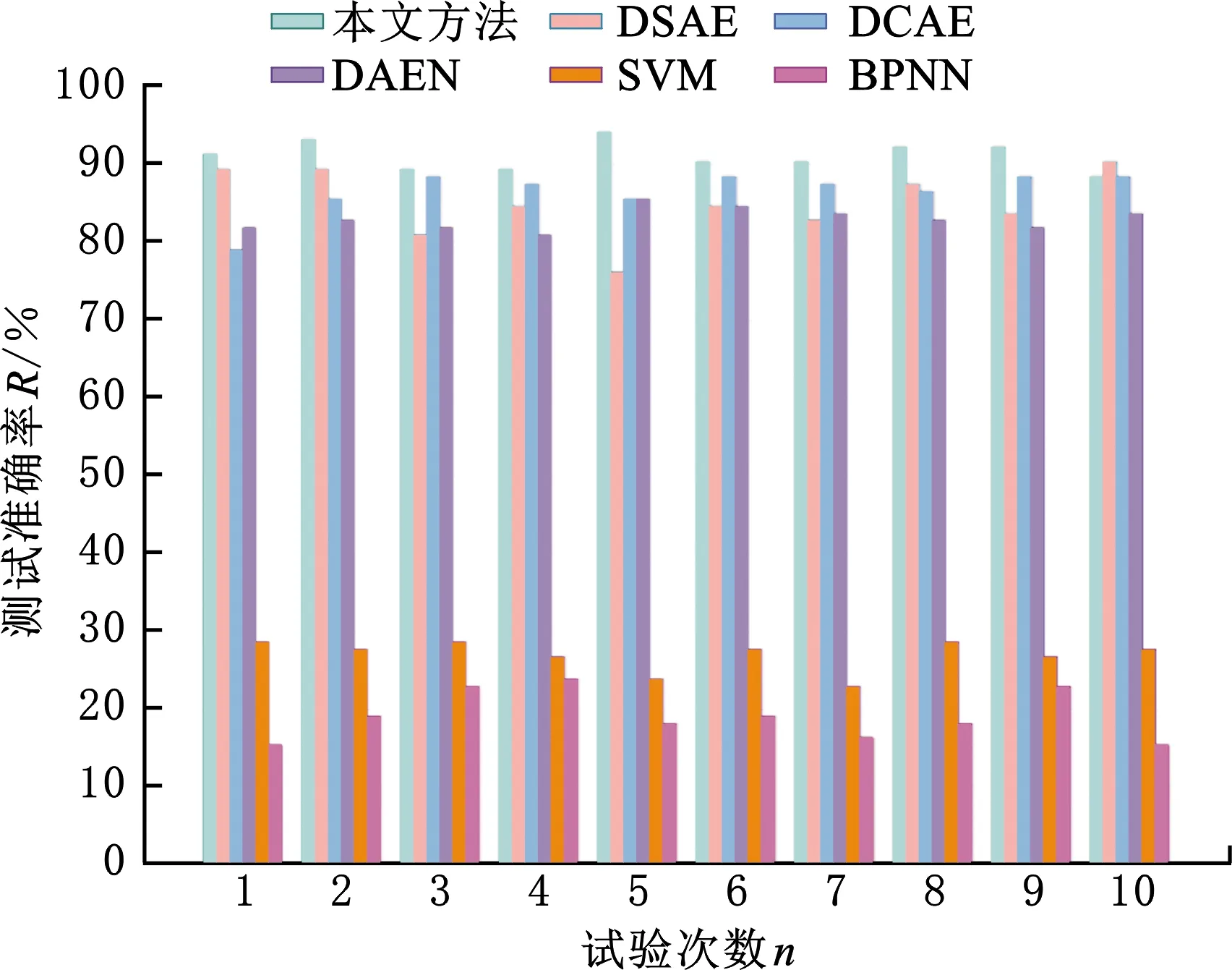
图10 六种方法10次试验对比图Fig.10 Comparison chart of 10 trails with different methods
从图10和表4可以看出,传统的机器学习方法SVM和BPNN的平均准确率仅为45.18%和48.45%,标准差分别为1.76和1.14。由此可知,对于变工况轴承振动数据的故障诊断问题,由于不同工况下振动信号特征差异大,传统的机器学习方法很难获取良好的故障特征表示,因此很难取得较高的诊断结果和网络稳定性。对于四种深度自编码器,DAEN在10次试验中表现较差,测试平均准确率为87.48%,且标准差较大,为1.52。这主要是由于DAEN未添加正则项约束,导致网络较难挖掘出数据中的稀疏特征。DSAE和DCAE的平均准确率相差不大,分别为91.20%和91.73%,标准差分别为2.22和0.85。由此可见,在处理变工况轴承振动数据的故障诊断问题时,增加稀疏惩罚项和收缩惩罚项均能提高测试准确率,但增加收缩惩罚项比增加稀疏惩罚项对网络稳定性的贡献更大。本文方法的测试平均准确率为93.75%,标准差为0.65,这说明将稀疏惩罚项与收缩惩罚项同时作用于自编码器的损失函数中可以更好地提取信号更具鉴别性的深层次特征,而且证明在网络权重中嵌入非负约束能够较好地减少重构误差。
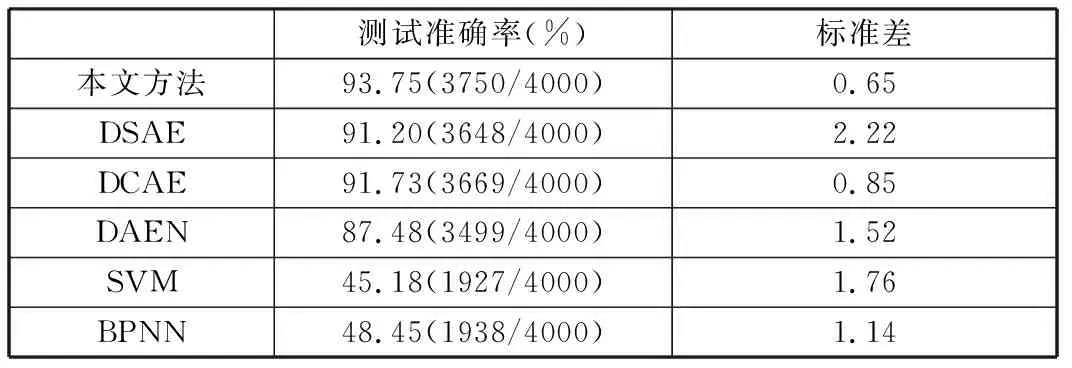
表4 六种方法的平均诊断准确率与标准差Tab.4 The average diagnostic accuracy and standard
图11为10次试验中本文方法第5次试验的混淆矩阵图。从图中可以看出,针对8种工况的轴承数据,本文方法在类别1、类别3、类别4、类别7和类别8都实现了100%的识别率。对于类别2、类别5和类别6中的每50个测试样本也能正确判断出40个以上。
与实验一相同,采用t-SNE分别提取原始数据与本文方法最后一个隐藏层的特征,分别绘制散点图,见图12、图13。从图12和图13中可以看出,原始时域信号的聚类效果很差,而本文方法提取的特征较容易区分,表现为相同故障类别的特征聚集程度较高、不同故障类别的特征相距较远。结合图11和图13可以看出,滚动体故障1和滚动体故障2中有少量样本点重叠,特征区分不明显,这也说明了图11表现出类别5和类别6中识别率仅84%和92%的原因。从总体上看,本文方法对变工况下的轴承振动数据也能达到较高的识别精度,具有较高的鲁棒性与稳定性。
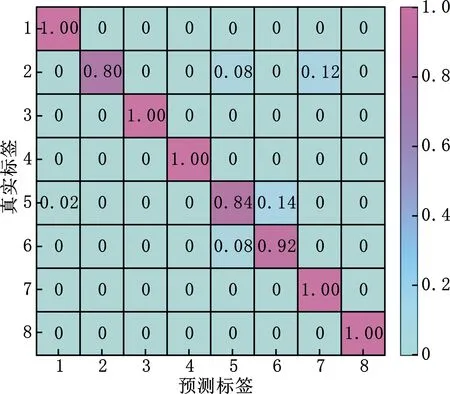
图11 本文方法第5次试验的混淆矩阵图Fig.11 Confusion matrix of the proposed method in the 5th trail

图12 原始数据可视化(实验二)Fig.12 Feature visualization map of raw data(experiment 2)
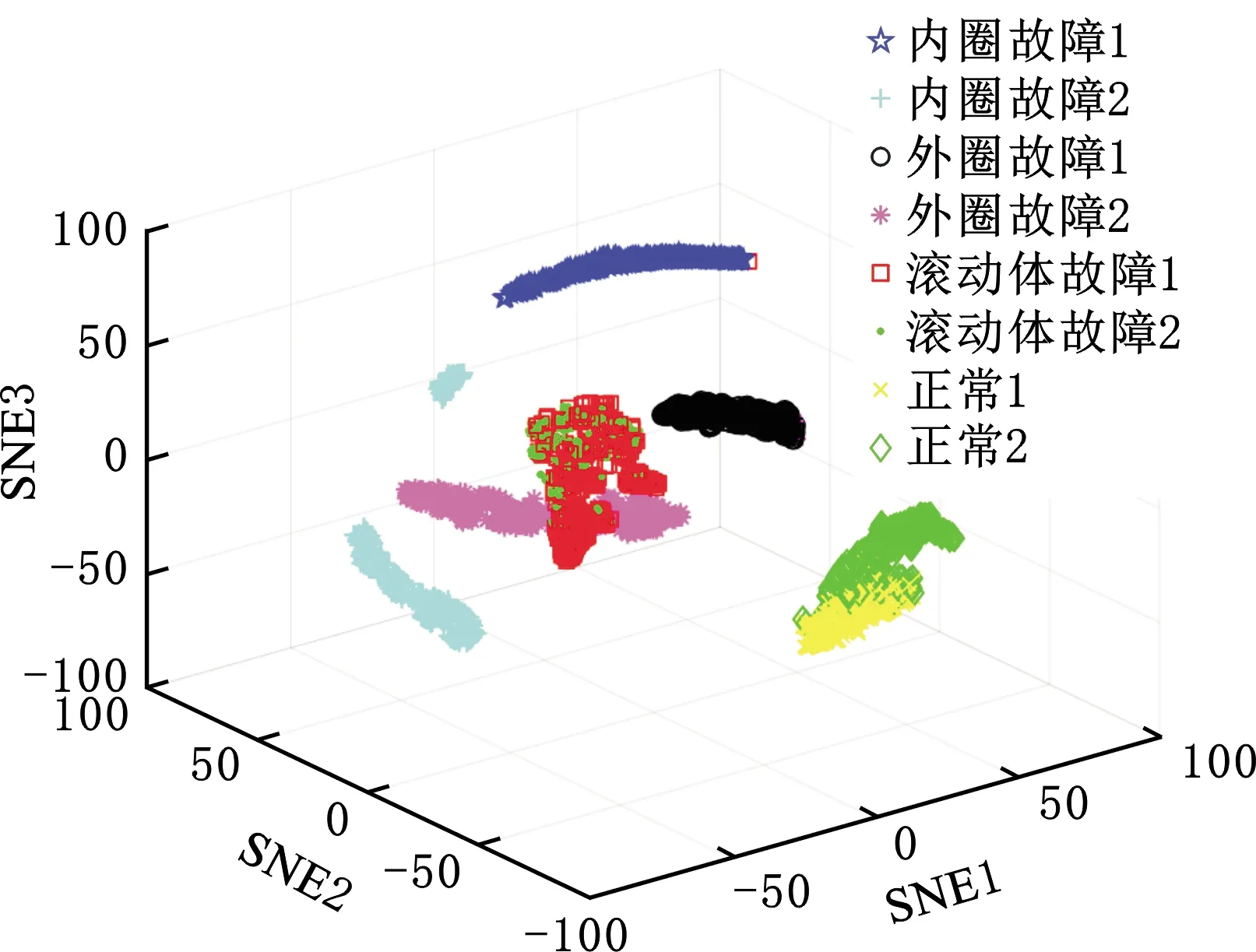
图13 本文方法特征可视化(实验二)Fig.13 Feature visualization map of the proposed method(experiment 2)
4 结论
本文提出了一种增强深度自编码网络,并将其应用于滚动轴承故障诊断。通过两组不同类型的实验验证,得到如下结论。
(1)以最大相关熵作为自编码器的损失函数以及加入稀疏惩罚项和嵌入非负约束因子的收缩惩罚项可以增强自编码器的性能,使其能够学习更具代表性的信息。
(2)基于GWO的参数寻优方法可以自适应地选取网络最优超参数,避免了手动调参的巨大工作量。
(3)针对不同实验设备采集的轴承振动数据,本文方法均能准确识别滚动轴承的故障类型,得到更好的诊断结果,验证了本文方法具有更强的特征提取能力,对变工况下的轴承振动数据也能达到较高的识别精度。
