刮板输送机仿生条纹型中部槽耐磨性试验研究
2021-11-18李娟莉刘朝阳麻豪洲赵保林
李娟莉 刘朝阳 李 博 麻豪洲 赵保林
1.太原理工大学机械与运载工程学院,太原,0300242.煤矿综采装备山西省重点实验室,太原,030024
0 引言
刮板输送机是一种将挠性刮板链条作为牵引机构的连续输送机械,是综合机械化采煤工作面的关键设备,中部槽是其重要组成部分[1-2]。中部槽长期受到刮板、链条与煤散料的混合摩擦作用,极易磨损失效,从而引起刮板输送机的运行故障,造成严重的经济损失,因此,提高中部槽的耐磨性至关重要。
目前常用的改善中部槽耐磨性的方法主要有:使用新型耐磨材料、改进中板制造工艺和采用表面处理技术等。葛世荣等[3]研究了热轧中锰耐磨钢和马氏体耐磨钢的冲击磨损性能,结果表明热轧中锰耐磨钢可显著降低中部槽磨损,大幅度延长刮板输送机运行寿命;朱瑾等[4]对不同Ti含量的耐磨钢进行了混合磨料磨损试验,并与耐磨钢Hardox450作了对比研究,结果表明新型含Ti耐磨钢的耐磨性可达Hardox450耐磨性的1.3倍;文献[5-8]研究表明等离子熔覆中部槽的显微硬度和耐磨性显著提高。随着摩擦学和仿生学的发展,许多学者发现,生物体表的非光滑结构能够很好地改善耐磨性能,为工程技术提供新的设计思想和工作原理,在工程领域得到了广泛应用[9-12]。
常见的非光滑仿生结构有凹坑型(蜣螂背板)、凸包型(蜣螂头部)、条纹型(扇贝壳、穿山甲鳞片)和鳞片型(鲨鱼体表)等。CHEN等[13]对凸包型及肋条型生物结构进行了仿生设计和磨料磨损试验,结果发现最优仿生结构表面对磨料磨损及侵蚀磨损均有一定的缓解效果;荣宝军[14]分别设计了凸包、棱纹、台阶及鳞片型非光滑表面,并进行了土壤磨料磨损试验,结果表明非光滑试样表面相比光滑试样表面磨损较轻;孙艺文等[15]在泥浆泵活塞工作表面加工不同尺寸的凹槽型仿生单元体,结果表明,凹槽型仿生泥浆泵活塞寿命延长了69.52%;吴波等[16]研究发现条纹型仿生活塞比标准活塞疲劳寿命平均延长了8.8%,磨损量平均减小了90%;熙鹏等[17]研究表明,相较于标准磨辊,条纹型仿生磨辊的耐磨性可提高72.1%。刮板和煤散料与中部槽的相互作用类似于扇贝壳与泥沙的相互作用,都属于物体与颗粒物的摩擦问题,因此本文在中板试样上设计仿生条纹型结构,研究仿生中板的耐磨性并得出其最优耐磨结构参数组合,为中部槽的耐磨优化设计提供依据。
响应面法是解决多变量问题的一种统计方法,相比于正交试验和全因子试验等统计分析法,具有次数少、时间短、准确性高等优点[18]。为了寻求耐磨仿生的最优工艺参数,本文利用单因素优化和响应面试验法进行条纹型仿生结构参数分析,建立平均磨损深度与各因素的二次多项式回归预测模型,并对其进行方差分析,探索影响条纹中板耐磨性的显著性因素顺序及各因素间的交互作用规律,最后通过真实试验确定参数的有效性。
1 材料与方法
1.1 试验方法分析
矿用刮板输送机在输送煤炭过程中,中板和槽帮的磨损多为三体磨损,即由于煤颗粒夹在刮板及中板或者槽帮之间对金属表面产生的磨损[19]。中部槽结构如图1所示。
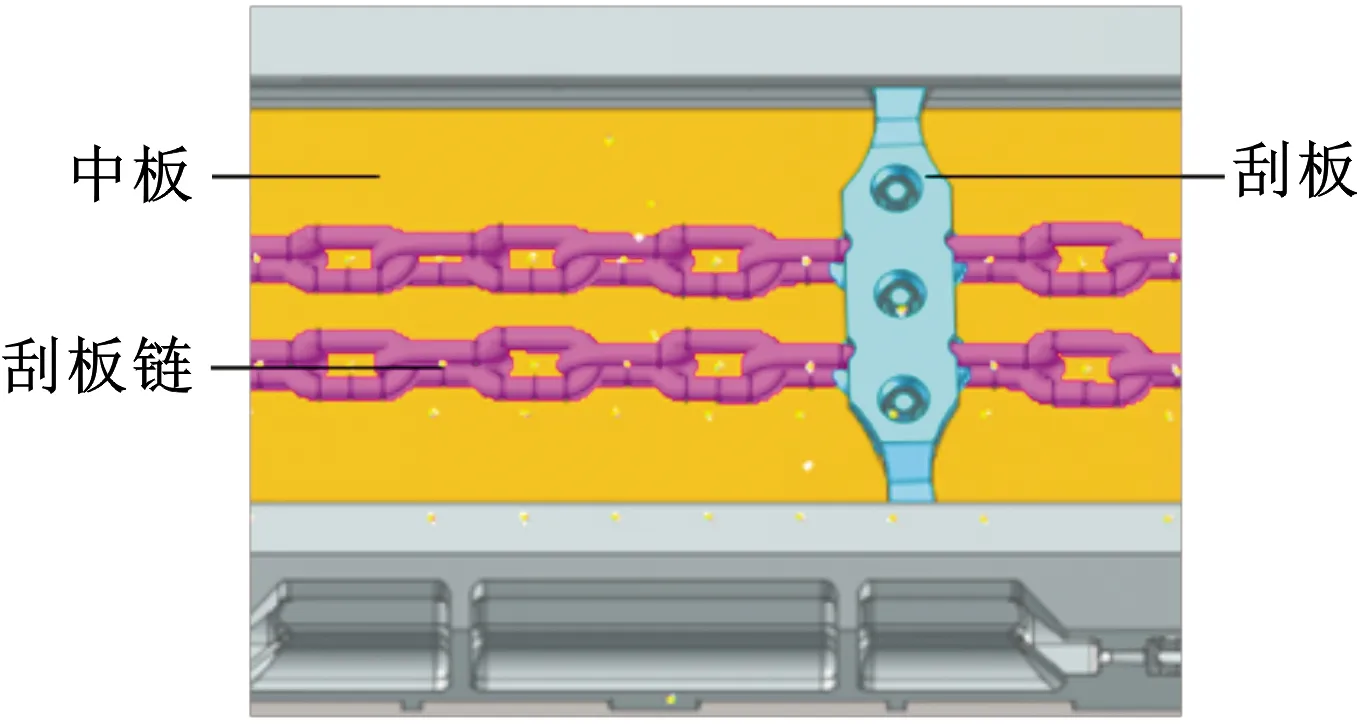
图1 中部槽结构Fig.1 Middle trough structure
刮板输送机体积庞大,试验运行成本过高,直接在中板上研究耐磨仿生参数不符合实际情况,因此本研究根据其工作原理设计了如图2a所示的改进销盘式ML-100型磨粒磨损试验机[20]。由于影响仿生条纹型结构耐磨性的参数较多,本研究需要进行多次单因素和响应面试验,且需要通过观察细观磨损形貌来分析耐磨仿生机理,所以本研究采用与实物模型等比例的仿真模型进行耐磨仿生参数的探究,仿真模型如图2b所示。磨粒磨损试验机的工作方式为回转式,下试样(中板)需制成圆心角为60°的扇形结构,材料为16Mn,如图2c所示;上试样刀具(刮板)设计成与刮板相似的斜切结构,如图2d所示,材料为与刮板材料相一致的42CrMo;驱动机构为料槽,料槽顺时针旋转带动煤料,如图2e所示。上试样在机架上可实现垂直于中板的振动但不可以转动,这样可以形成上试样、煤料、下试样的三体磨粒磨损。

(a) 实物图 (b) 仿真模型 (c) 中板试样

(d) 斜切结构 (e) 机器运转示意图图2 磨粒磨损机Fig.2 Abrasive wear machine
1.2 EDEM-RecurDyn耦合仿真
条纹型中板是基于扇贝壳结构特征而设计的,其结构具有正余弦函数特性,给加工带来了较大的难度,且中板制备会消耗大量时间,因此本文利用离散元(EDEM 2018)与动力学(RecurDyn V9R1)耦合的方式模拟中板磨损过程,探究条纹型中板耐磨仿生结构参数。离散元与动力学耦合模型及相关参数的可靠性已得到同课题组成员的验证[21]。
1.2.1EDEM离散元参数设置
(1)颗粒模型。散料中颗粒的形状对颗粒间的相互作用有显著影响[22],因此EDEM中建立的颗粒模型应尽可能逼近真实颗粒的形状。考虑到煤颗粒形状的不确定性和复杂性,本研究以典型煤块为模拟对象,选择十球填充颗粒模型,如图3所示。以颗粒工厂随机产生颗粒,质量700 g,粒径范围6~8 mm。

(a) 煤颗粒模型 (b) 典型煤颗粒图3 煤颗粒模型与典型煤颗粒Fig.3 Coal particle model and typical coal particle
(2)EDEM接触模型选择及参数设置。颗粒间的接触模型选择Hertz-Mindlin(no slip)无滑动接触模型,颗粒与几何体接触模型选择Hertz-Mindlin with Archard Wear磨损模型。煤与几何体的本征参数及接触属性参数参考文献[23-24],如表1、表2所示。中板与煤料的磨损常数设置为1.2×10-12m2/N,时间步长为22%,仿真时长为1.32 s(颗粒生成时间0.5 s,料槽旋转时间0.82 s)。

表1 煤和钢的本征参数Tab.1 Intrinsic parameters of coal and steel

表2 接触参数Tab.2 Contact parameters
1.2.2RecurDyn动力学参数设置
机架设置为固定于地面的固定副;上试样夹具与机架之间分别设置移动副(控制上试样上下跳动)和接触副(控制上下跳动的滑动摩擦因数),接触副的接触方式为体-体接触;六块扇形中板试样设置为固定于料槽的固定副;上试样与下试样设置接触副;料槽设置转动副,转动副的转动特性由step函数控制step(0.5,0,0.5,5.91);所有接触副的滑动摩擦因数设置为0.15,其余选择默认设置。
1.3 仿生中板设计
逆向造型技术对重构空间实体几何具有较好的效果[25-27]。本研究利用逆向造型技术提取扇贝壳及穿山甲鳞片表面的几何结构。具体步骤如下。
(1)通过CPC三维扫描仪扫描扇贝壳及穿山甲鳞片标本。
(2)利用GeomagicStudio2013软件对扫描得到的点云进行拼接、清除杂点和合并处理,如图4、图5所示。

(a) 正视图 (b) 侧视图图4 扇贝壳点云处理结果Fig.4 Scallop shell point cloud process results

(a) 正视图 (b) 后视图图5 穿山甲鳞片点云处理结果Fig.5 Pangolin scale point cloud process results
(3)沿图6所示方向,利用Imageware13.2软件对处理后的点云进行特征提取,将提取后的特征点云保存为“.dxf”格式并导入CAD2018中。利用MOVE及ID命令确定几何点端点为坐标原点,得到各点的相对坐标值。
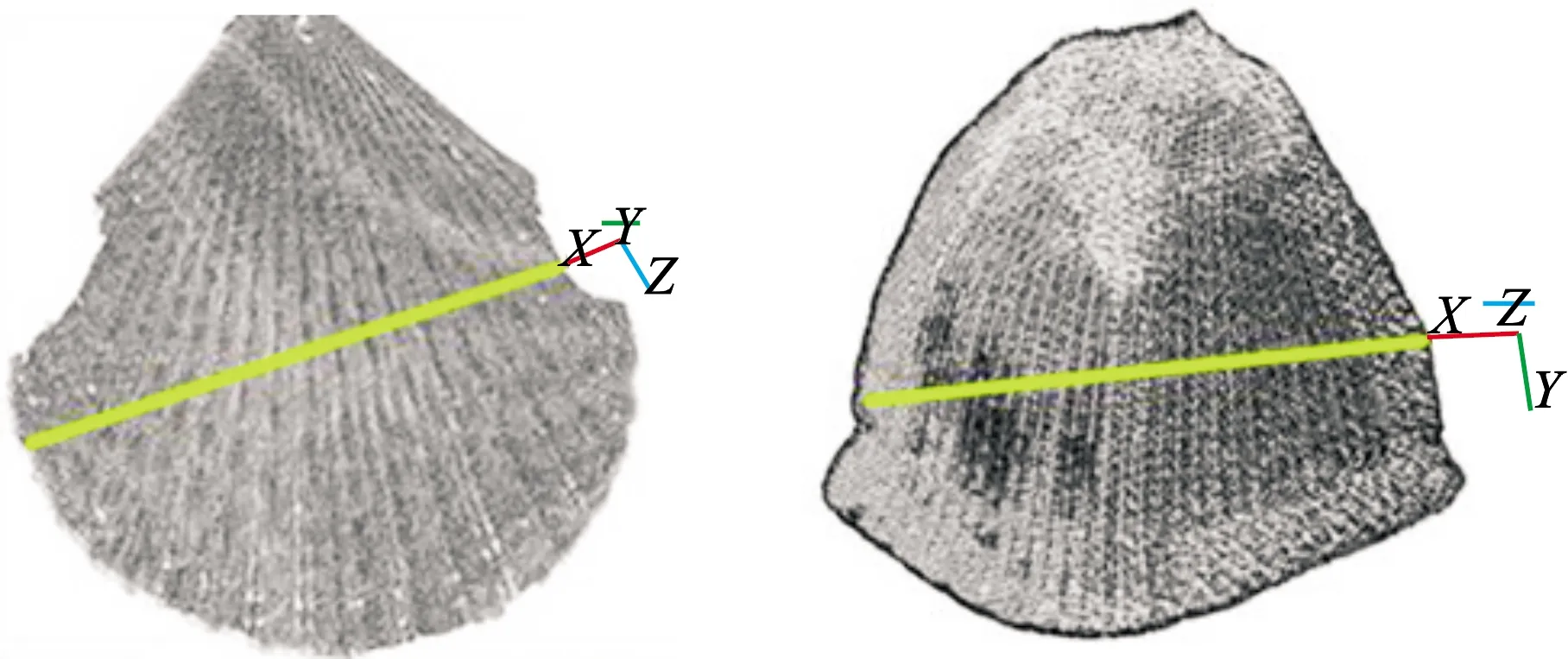
(a) 扇贝壳特征结构取向 (b) 穿山甲鳞片特征结构取向图6 特征结构取向Fig.6 Feature structure extraction direction
(4)将CAD生成的坐标数据导入MATLAB R2018b中,并对其进行三角函数拟合,得到图7所示的点云拟合曲线(W为所测样本的点云宽度坐标,H为所测样本的点云高度坐标),方程、方程系数及评价值如表3所示。
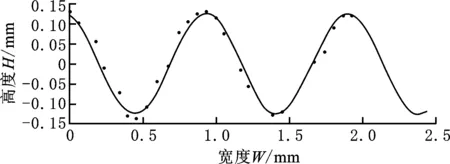
(a) 穿山甲鳞片结构数学模型

(b) 扇贝壳结构数学模型图7 穿山甲鳞片与扇贝壳结构数学模型Fig.7 Mathematical model of pangolin scales and scallop shell structure

表3 穿山甲鳞片与扇贝壳方程拟合系数Tab.3 Fitting coefficient of pangolin scale
由图7可知,扇贝壳及穿山甲鳞片表面几何结构呈正余弦函数形式,且两者函数二分之一周期(条纹宽度)与函数峰值(条纹高度)比值分别为3.4和3.9,即两者的正余弦条纹都呈扁平状。本研究在中板表面设计并排布具有正余弦函数特征的条纹凸体,并将条纹宽高比r、条纹宽度W及条纹节距L作为反映条纹结构的特征参数[28-30]。设计简图见图8。
1.4 仿真优化设计
1.4.1单因素优化仿真设计
以平均磨损深度为响应值,分别研究条纹宽高比、条纹宽度及条纹节距对条纹型仿生板耐磨性的影响规律。通过单因素法初步优化影响因素的计算域,进而为响应面法优化设计提供合理的取值范围,提高优化质量。
(1)条纹宽高比r。扇贝壳与穿山甲鳞片条纹宽高比分别为3.4与3.9,可知两者条纹都较扁平。宽高比取5水平并将3.4与3.9包含在内,如表4所示。
(2)条纹宽度W。由图8可知,上试样、散料与下试样的接触宽度约为20 mm,摩擦接触区至少有两列条纹排布,此时条纹最宽,因此条纹宽度小于10 mm,选取5水平,如表4所示。
(3)条纹节距L。上试样、散料与下试样的接触宽度为20 mm,条纹最大节距小于20 mm,选取5水平,如表4所示。

表4 单因素优化设计水平Tab.4 Optimization design level of single factor
根据单因素试验结果,以平均磨损深度为响应值,采用Box-Benhnken试验设计原理设计响应面试验,各因素分别取高水平(1)、中心点(0)与低水平(-1)3个水平,各因素水平取值编码如表5所示。

表5 响应面法优化设计水平Tab.5 Optimization design level of response surface
2 结果分析
2.1 单因素优化结果分析
单因素优化结果见图9。由图9a可知,随着宽高比的增大,仿生板的平均磨损深度总体呈下降趋势。宽高比过小,条纹凸体变得很尖,上试样刀具与条纹凸体的接触面积过小,不利于减小磨损;宽高比过大时,条纹凸体变得很扁,与上试样刀具的接触面积过大,在一定程度上,上试样刀具与条纹凸体间的空隙减小,不利于形成空气膜,减磨效果不显著,因而根据试验结果,宽高比取4.75为响应面法设计的0值。
由图9b可知,在条纹宽度范围内仿生板的平均磨损深度先减小后增大,在宽度为0.5~1.75 mm内平均磨损深度急剧减小,当宽度大于1.75 mm时平均磨损深度增大。宽度直接影响上试样刀具与条纹凸体的接触面积及外观形貌,宽度过大,上试样刀具与条纹凸体间的空隙减小,不利于形成空气膜,无法减小磨损;宽度过小,在宽高比一定的情况下,高度变得很低,上试样刀具与条纹凸体间的空隙依然很小,减小磨损效果不显著,因而条纹宽度不宜过大也不宜过小。综上分析,宽度取1.75 mm为响应面法设计的0值。

(a) 宽高比r

(b) 宽度W/mm
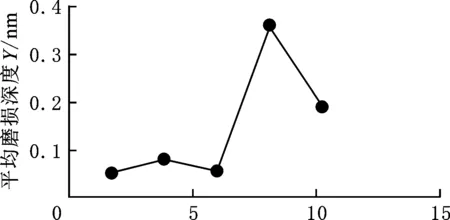
(c) 节距 L/mm图9 条纹中板单因素磨损结果Fig.9 Results of single factor wear in striations
由图9c可知,在条纹节距水平范围内,随着节距的增大,总体平均磨损深度呈增大趋势。节距越大,与上试样刀具接触的条纹凸体越少,形成的空气膜越少,减小磨损效果越差;但过小的节距会导致接触面积增大,分流作用降低,磨损增大。根据试验结果,当节距为1.75 mm和6 mm时平均磨损深度均较小,为下一步响应面法优化水平设计方便,取节距为6 mm为响应面法设计的0值。
2.2 响应面法结果分析
2.2.1Box-Behnken设计及回归模型
Box-Behnken Design(BBD)试验的设计及仿真结果如表6所示。依据仿真结果利用Design-Expert12.0软件对BBD试验结果进行二次多项回归,获得以平均磨损深度Y为响应值,宽高比r、宽度W、节距L为自变量的三元二次回归方程,如下所示:
Y=3.819 80×10-6-8.216 51×10-7r-
1.479 57×10-6W-1.365 25×10-7L+
8.402 50×10-8rW+1.18615×10-8rL+
5.980 77×10-9WL+6.010 79×10-8r2+
2.835 20×10-7W2+5.291 87×10-9L2

表6 Box-Behnken试验设计及结果Tab.6 Box-Behnken experimental design and results
对回归模型进行方差分析,结果如表7所示。由表7可得,回归模型的P值小于0.0001,表明多项式回归预测模型描述平均磨损深度与各因素的关系极显著;失拟项的P值为0.5554>0.05,表明多项式模型拟合较好,误差较小;决定系数R2=0.9955,接近1,说明拟合方程可靠度较高。
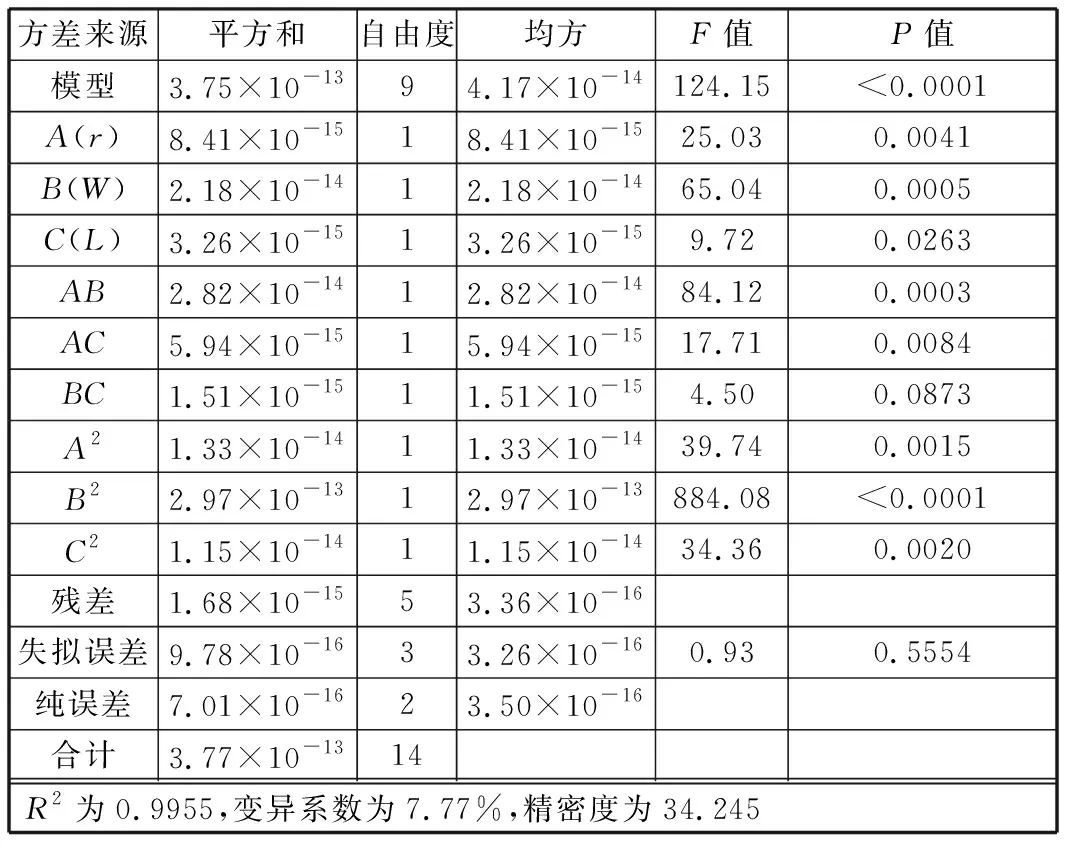
表7 回归方程方差分析Tab.7 ANOVA of regression equation
综上所述,该方程可以用来预测仿生板的平均磨损深度。在显著性水平α=0.05的水平上,r、W、L、rW、rL、R2对平均磨损深度影响显著,表明各影响因素之间成二次关系,且影响显著性由大到小依次为W、r、L。分析其原因发现,条纹凸体宽高比对凸体的形貌构成有很大影响,外观形貌较扁时(宽高比和宽度较大),上试样刀具与条纹凸体间的空隙较小,难以形成空气膜,减小磨损效果不显著;外观形貌较尖时,上试样刀具对下试样的切割作用增大,不利于减小磨损。此外,在宽高比一定的条件下,宽度也会影响外观形貌,从而影响磨损。而在试验条件下,最大与最小节距所形成的条纹凸体与上试样刀具接触的数量差较小,对磨损的影响略低于条纹宽高比与宽度的影响。
对照组(不加药)在不同时间点对PC3细胞的凋亡作用差异无统计学意义(P>0.05);雷公藤内脂醇的浓度为10、20、40 nmol/L时,培养PC3细胞12 h、24 h、48 h后对PC3细胞的凋亡作用差异有统计学意义(P<0.05),见表2。
2.2.2回归模型交互效应分析
三维响应面可表示平均磨损深度与仿生结构各因素的函数关系及规律趋势,由图10可以得到仿生板的最优耐磨结构参数。由图10可知,各因素交互作用的响应曲面都呈反抛物线,即都有极小值点,可得到平均磨损深度取最小值时各因素值的取值范围。当各因素值取较大值时,平均磨损深度随各因素值的增大而增大,当各因素值取较小值时,平均磨损深度随各因素值的减小而增大;但在每个交互作用中,因素值取较小值时平均磨损深度增大的速率较大。
等高线的形状可反映交互项对响应值(即平均磨损深度)的影响显著性,通常椭圆形比圆形的影响显著性更明显,且椭圆的长短轴之比越大影响显著性越高。由图10可得,条纹宽高比与条纹宽度交互作用相较于宽高比与节距交互作用、节距与宽度的交互作用更显著。

(a) 条纹宽高比与宽度 (b) 条纹宽高比与节距 (c) 条纹宽度与节距图10 各因素交互作用图Fig.10 Interaction diagram of the factors
3 验证与对比试验
3.1 最优结构参数预测与验证
以平均磨损深度为响应值,在特定条件下仿真优化得到条纹中板的最优耐磨结构参数为r=4.94,W=1.81 mm,L=6.33 mm。将最优参数下的条纹仿生中板与光滑中板进行重复仿真对比,如表8所示。由表8可知,条纹中板的平均磨损深度均值较光滑中板减小2.28×10-8mm,磨损深度减小约94.6%。

表8 条纹型中板与光滑中板对比Tab.8 Comparison of striated middle plate and slide plate mm
3.2 对比试验
采用改进销盘式ML-100型磨粒磨损试验机进行对比验证,将加工好的最优耐磨参数组合下的条纹中板(图11)与光滑中板交替排布。试验采用700 g陕西省榆林市神木县长焰煤,粒径选择6~8 mm,设置磨粒磨损试验机转速为56 r/min(即线速度0.65 m/s),载荷20 N,时长660 min,煤料为干煤料,环境温度为常温25 ℃,空气湿度60%。

图11 仿生条纹中板试样Fig.11 Bionic striated middle plate sample
试验前用600目砂纸打磨中板试样表面,确保表面粗糙度一致。试验后用无水乙醇清理中板试样表面的煤粉以减小误差。
采用万分之一天平(FA3204B)对试验前后的3块中板试样重复称量3次,得到平均值并求出试验前后的质量差来衡量磨损程度,如图12所示,可知试验结果中仿生条纹板比于光滑板磨损质量减小了约78.54%。

图12 中板对比试验质量差Fig.12 Mass differences of middle plate comparison tests
对比仿真与试验结果发现,仿真结果中仿生中板比光滑中板平均磨损值减小约94.6%,试验结果中仿生中板比光滑中板磨损量减小约78.54%。定义仿真值与试验值的相对误差为误差率η,结合仿真与试验平均磨损深度的减小率求得η为20.45%,误差较大,但仿真试验处在理想环境,仿真时间较短,且在仿真中未考虑煤炭的破碎,因而存在局限性,而与光滑中板磨损的对比结果说明仿生条纹型中板的最优耐磨参数是有效的,可以为仿生中板的研制提供参考。
4 条纹型仿生中板耐磨机理
刮板与煤粒的卡滞及煤料对中板表面的正压力是导致中板磨损严重的重要原因,因此研究上试样(刮板)的阻力及下试样(中板)表面的颗粒压力十分必要。仿生板与光滑板采用图13所示的间隔方式排布,为了提高仿真速度,仿生板与光滑板分别布置两块。下试样、上试样与煤颗粒三体磨损的时间段分别为:仿生板0.58~0.76 s、0.94~1.12 s,光滑板0.76~0.94 s、1.12~1.3 s,因此只分析0.58~1.3 s之间的仿真数据。从RecurDyn软件后处理的耦合模块中导出上试样的合力值与阻力值(图14)和煤颗粒对下试样表面法向压力值(图15)。

图13 条纹中板布置方式Fig.13 The arrangement of the striated plate

图14 上试样受力 Fig.14 Force applied to the up sample
由图14可得,仿生条纹中板的上试样阻力的波动频率和波动幅度都较小,上试样所受颗粒的合力与阻力规律类似。条纹中板与光滑中板在同一环境下运行,条纹中板表面的上试样平均阻力(94.3 N)小于光滑中板表面的上试样平均阻力(107.4 N)。由图15可得,颗粒对光滑中板表面法向压力(简称压力)的波动频率大于颗粒对条纹中板的压力波动频率。颗粒对条纹中板压力最大值(1200.1 N)小于颗粒对光滑中板压力最大值(1684.2 N)。分析原因发现,上试样刀具的楔形结构与下试样形成一定的夹角,极易发生煤料卡滞。当煤料在上试样与下试样之间时,随着料槽转动,上试样与下试样对煤粒的挤压力逐渐增大,且煤颗粒持续切削下试样表面,因此光滑中板表面受到的颗粒压力及上试样受到的阻力较大。而条纹中板由于条纹凸体的存在,对煤散料的流动具有分流和导向作用,在煤散料与上试样和条纹中板发生卡滞前,条纹倾斜表面可将颗粒对条纹表面的作用力分解,使煤颗粒发生滑动,因此煤散料不易在上试样和条纹中板之间卡滞。

图15 中板颗粒压力Fig.15 Middle plate particle pressure
从EDEM软件的后处理模块Archard Wear模型中得到图16所示条纹中板与光滑中板在同一运行环境下的磨损云图,图中红色表示磨损较严重的地方(犁沟)。由图16可得,光滑中板表面存在连续切削的磨痕,条纹间的光滑区域出现少量断续的磨痕且磨痕较细,说明该处发生的磨损较轻。条纹中板的磨痕主要发生在条纹表面,且由于料槽的旋转作用产生了离心力导致条纹处的磨痕集中在条纹内侧,即煤散料主要与条纹内侧发生接触磨损。

(a) 光滑中板磨损云图

(b) 条纹中板磨损云图图16 中板磨损云图Fig.16 Middle plate wear cloud map
作用在条纹表面上的总摩擦力FT=FA+FB,其中,FA是作用在中板表面平坦部分上的摩擦力,FB是作用在中板条纹凸体上的摩擦力。令SD表示煤颗粒与条纹中板在滑动方向上的距离,SH表示条纹凸体的高度,SR表示煤颗粒的特征尺寸(有效直径)。当SD远大于SR时,截取某个时间段内颗粒流向,如图17所示,在0.6~0.65 s这一时间段,颗粒的运动方向在刮板附近发生了改变。刮板试样推动煤散料向前运动,因而阻力较大,基于能量最小原理,粒子流的流动应选择阻力最小的路径,所以煤颗粒有向两边运动的趋势,但由于刮板试样的推动,因而会向前运动一段距离,进而产生磨损。条纹凸体由于其形状、尺寸和布置而引导煤散料流动,在滑动的煤颗粒遇到条纹中板的凸起处会产生较大的应力,因而凸起位置的磨损将大于平坦位置的磨损。在这种情况下,条纹中板的磨损由突起的磨损决定。但是,如果条纹中板的凸起在形状和尺寸上得到合理设计,则与光滑表面相比,FT可以减小,并且相应地,条纹凸体的磨粒磨损将减少,尤其是条纹凸体使用耐磨耐腐蚀材料。因此,条纹凸体对煤散料流动的分流和导向作用缓解了中板表面的受力,使磨损深度减小。

(a) t=0.6 s (b) t=0.65 s图17 颗粒流向图Fig.17 Particle flow diagram
5 结论
(1)本文利用逆向造型技术提取扇贝壳及穿山甲鳞片表面的几何结构,发现扇贝壳及穿山甲鳞片表面几何结构呈正余弦函数形式,且两者函数二分之一周期(条纹宽度)与函数峰值(条纹高度)比值分别为3.4和3.9,即二者正余弦条纹都呈扁平状。
(2)通过单因素法和响应面法优化试验,以磨损深度为响应值,对仿生条纹型中板的宽高比、宽度和节距进行了探讨。结果发现:显著性影响由大到小依次为宽度、宽高比、节距,条纹宽高比与条纹宽度交互作用最为显著。在试验条件下,当宽高比为4.94、宽度为1.81 mm、节距为6.33 mm时磨损深度最小。
(3)对最优耐磨参数下的条纹中板与光滑中板的耐磨性进行仿真和试验对比,结果表明,最优参数组合下的条纹中板具有良好的耐磨性能,与光滑中板相比,磨损质量减小了78.54%。仿真中未考虑煤炭的破碎和含水,在今后的工作中,可将此部分完善,使结果更精确。
(4)分析仿生条纹型中板的耐磨机理发现,由于条纹凸体的存在,条纹中板对煤散料的流动具有分流和导向作用,缓解了中板表面的受力和上试样的受力,从而减少了磨损。
