基于近似牛顿方向的综合能源系统最优能流解耦算法

张抒凌，温步瀛,2，江岳文,2

(1.福州大学 电气工程与自动化学院，福建 福州 350108；2.智能配电网装备福建省高校工程研究中心，福建 福州 350108)

随着人类社会发展，能源需求增长与能源资源紧缺、能源消耗与生态环境保护的矛盾日益尖锐，对高效、低碳、清洁能源系统的研究成为当今能源发展的主题[1]，我国也制定了在2030年前实现碳达峰与在2060年实现碳中和的战略目标[2]。在传统模式下，不同能源系统彼此单独规划设计和运行，能源之间无法互补利用；综合能源系统(integrated energy system，IES)打破隔阂，作为电、热、气、冷等多类能源形式的生产和利用场所，通过能源设备交互耦合实现了各类能源的优势互补，提高新能源的利用率和可再生能源的渗透率，减少环境污染，保障社会供能安全可靠[3]。

IES最优能流是IES运行分析中的一个基本问题，指导不同能源之间的充分互补和协同优化调度，对于IES的经济、安全稳定运行有重要意义[4]。由于IES最优能流问题与电力系统最优潮流问题相似度高，计算方式可以类比电力系统求解方法，已经有许多学者对IES最优能流问题进行了研究。文献[5]针对辐射状结构热网构建了电-热IES运行优化模型，文献[6]针对热网构建了精细化稳态能流计算模型，2篇文献均采用内点法对电-热耦合IES最优能流模型进行求解。文献[7]将非线性、非凸的电-热IES最优能流问题线性化后求解。文献[8]建立了量调节模式下区域电-热系统模型，将具有凹凸规划形式的联合最优潮流优化模型转为二阶锥规划问题进行序贯求解。文献[9]对电-热-气IES的协调运行问题作出初步探究。文献[10]以电-气IES环境系统总运行成本最低为目标，以系统安全约束以及污染物排放浓度限值作为约束条件，探究了不同场景下环境因素对模型求解结果的影响。文献[11]基于能源集线器概念，对区域电-热-气IES进行建模求解，设置经济最优的目标与合理的运行约束，对所建立模型的能量流进行优化。

上述文献采用信息完全的集中式优化求解方法，将集中式优化方法应用于求解IES最优能流问题时，需要有一个联合调度中心收集IES的数据，建立统一模型[12]。由于IES涵盖几种能源网络，包含设备多，互联后的网络规模增大，数据维护难度增大，同时，系统间的信息保护和隐私安全问题也不容忽视。随着IES规模的扩大，各系统将由不同能源供应商负责，他们出于用户隐私、防范数据泄露等原因，而不愿意向其他系统传递自己的信息[13]。各能源系统具有设备信息参数保密的诉求，能源系统之间仅有少量的信息交互，集中式优化方法便不再适用。在IES中，能源系统既彼此互联又需保有独立性，在系统之间无法完全透明传递信息的制约下，如何对电-热-气IES进行相对独立的优化，达到整体效益的最大化，同时保证系统的安全运行，是一个具有挑战性的问题。因此，研究求解IES最优能流分布式优化方法是非常必要的。

分布式优化就是将大型优化问题分解为若干子问题，分别对子问题优化求解，从而得到原问题的解[14]。在优化过程中，集中式优化算法计算占用内存大、大规模数据传输导致的带宽限制、传输误码和信息泄漏等各种问题也能够通过采用分布式优化算法避免。

近似牛顿方向(approximate Newton directions，AND)算法[15]是一种求解大规模连续优化问题的解耦算法，它可以将大规模的全局优化问题解耦为若干子问题，通过部分变量的传递与子问题的交替求解，获得满足收敛条件的最优解。AND算法简单有效，易于执行，具有较强的鲁棒性和收敛性，已被运用于电力系统多区域最优潮流求解[16]、无功优化[17]、电力动态经济调度[18]，还被延伸应用于电-气IES经济调度[19]、水火最优潮流[20]等问题中。

本文采用AND算法建立电力系统、热力系统、天然气系统规划子问题，进行电-热-气IES最优能流问题分布式优化求解，作为IES最优能流计算的一种有益探究和补充。本文所提算法可以在其他能源系统参数未知的情况下，通过第三方管理机构传递必要信息，在电、热、气子问题中独立求解优化问题，最终达到电-热-气IES能流整体优化的效果。该算法的修正方向与精确牛顿方向高度一致，且每个子问题不需要求最优解，只需要迭代1次，缩短了计算时间；算法执行简单，只需要交换子系统之间的必要参数，能够有效保护系统隐私。

1 电热气IES模型

本文建立的IES模型由电力系统、热力系统、天然气系统和进行能源转化的耦合设备组成，IES示意图如图1所示。以风电、光伏为代表的可再生能源与燃气轮机发电注入电网，与大电网相连；热负荷由电锅炉、燃气锅炉供应；天然气负荷由天然气源供应；耦合设备包括燃气轮机、燃气锅炉、电锅炉。

1.1 电力网络模型

交流电网节点功率计算公式为：

(1)

(2)

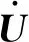
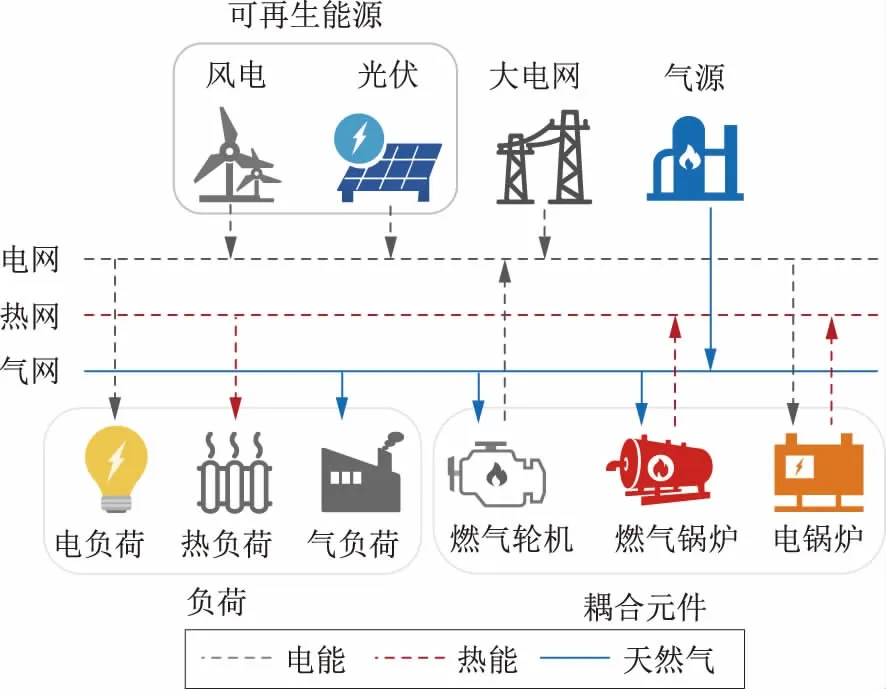
图1 电-热-气IES示意图Fig.1 Schematic diagram of electricity-heat-gas IES

1.2 热力网络模型

a)水力模型。类比基尔霍夫第一定律，水流需满足流量平衡方程：每个节点注入流量等于流出流量[21]，即

Ahm=mq.

(3)

式中：Ah为热网的节点-支路关联矩阵；m为各管道中的水流量向量；mq为各节点流出的水流量向量。

类比基尔霍夫第二定律，水流需满足环路压降平衡方程：在管道连成的每个封闭回路中，水流的压头损失之和为0，即

Bhhf=0,

(4)

hf=Khm|m|.

(5)

式(4)、(5)中：Bh为热网的回路-支路关联矩阵；hf为管道压降向量；Kh为热网管道的阻力系数矩阵。

b)热力模型。热力模型用于计算每个节点的温度，每个节点对应3种温度向量：供热温度Ts为水流进入各负荷节点前的温度，出口温度To为水流流出各负荷节点时的温度，回热温度Tr为水流在管道交汇节点处与其他管道的水混合后的温度。

节点热功率表达式为

Φ=cpmq(Ts-To).

(6)

式中：Φ为各节点热功率向量；cp为水的比热容。

管道温降计算公式为

(7)

式中：Tstart、Tend分别为水流进入、流出一条管道时的温度；Ta为环境温度；λ为管道热传导系数；Lh为热网管道长度；m为管道中的水流量。

多条管道交汇处，混合节点温度计算满足

(∑mout)Tout=∑minTin.

(8)

式中：min为流入混合节点前各管道的水流量；Tin为流入混合节点前各管道的水温；∑mout为流出混合节点的水流量之和；Tout为流出混合节点的水温。

1.3 天然气网络模型

对于0.7 MPa以上的高压网络，采用Weymouth模型计算天然气管道d稳态流量fpd[22]，即：

fpd=Kpd×sgn(pk,pn)×

(9)

(10)

式(9)、(10)中：pk、pn为节点压力，k、n为管道d的首、末端节点编号；sgn函数反映了气体在管道中的流动方向，取“+1”时表示气体从首端流向末端，取“-1”时流向相反；Kpd为管道常数；Ngn为天然气网络节点集合。

天然气网节点供气平衡方程为

Agf=G.

(11)

式中：Ag为天然气网的节点-支路关联矩阵；f为天然气流量向量；G为各节点流出的天然气流量向量。

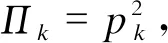
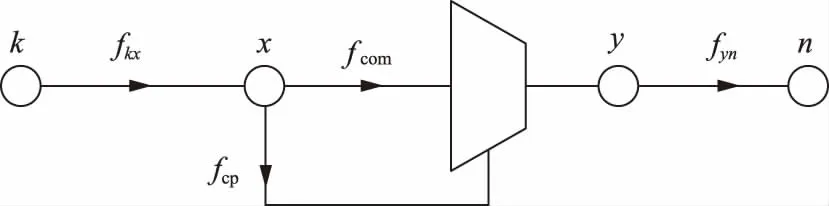
图2 燃气轮机驱动压缩机管道模型Fig.2 The model of pipeline with compressor driven by gas turbine

(12)

式中：fcom为流经压缩机管道的天然气流量；fcp为压缩机消耗的天然气流量；fkx、fyn分别为压缩机入口与出口管道的天然气流量；Kkx、Kyn分别为压缩机入口、出口管道的管道常数；pk、px、py、pn对应图2中4个节点的压力；zcom为压缩机的耗气系数，本文为了建立便于内点法求解的模型，取其值为常数。

1.4 耦合元件模型

本文构建的电-热-气IES模型中含有电锅炉、燃气锅炉、燃气轮机3类耦合元件，以下为它们的能源转化关系式：

ΦEB,a=PEB,aηEB,a,a∈NEB;

(13)

ΦGB,t=FGB,tηGB,t,t∈NGB;

(14)

PMT,v=FMT,vηMT,v,v∈NMT.

(15)

式(13)—(15)中：ΦEB为电锅炉产生的热功率，用下标a表示第a台电锅炉；PEB为电锅炉消耗的电功率；ΦGB为燃气锅炉产生的热功率，用下标t表示第t台燃气锅炉；FGB为燃气锅炉消耗的天然气功率；PMT为燃气轮机产生的电功率，用下标v表示第v台燃气轮机；FMT为燃气锅炉消耗的天然气功率；ηEB、ηGB、ηMT分别为电锅炉、燃气锅炉、燃气轮机的能源转化效率；NEB、NGB、NMT分别为电锅炉、燃气锅炉、燃气轮机集合。

2 IES最优能流的数学模型

2.1 目标函数

基于电-热-气IES集中规划运行的视角，在满足电、热、气网络安全运行的前提下，目标函数设为运行成本fD最小，运行成本包括电力系统向大电网购电成本fe和天然气系统向气网购气成本fg：

minfD=fe+fg，

(16)

fe=CePe，

(17)

(18)

式(16)—(18)中：Ce、Cgk分别为大电网购电价格、气源k处天然气价格；Pe为大电网购电量；Ggk为气源k处供气量；Ngs为气源点集合。

2.2 等式约束

变量矩阵x=[PGQRθUmPEBmTs,loadTr,loadΦEBΦGBΠGgFGBFMT]T。其中：PG、QR分别为电网中有功功率源、无功功率源的出力向量；PG=[PePwindPPVPMT]T，Pwind、PPV分别为风电场、光伏电站发出的有功功率向量；θ、Um分别为电网中各节点的电压相角、电压幅值向量。则满足

(19)

式中：ΔP、ΔQ分别为电力系统各节点有功功率、无功功率偏差向量；ΔΦ、Δp、ΔTs、ΔTr分别为热力系统各节点功率偏差、回路压力降偏差、供热温度偏差和回热温度偏差向量；Δf为气网各节点流量偏差向量；PSP和QSP分别为电网中注入各节点的有功功率和无功功率向量；ΦSP为给定的热网节点功率向量；GSP为给定的天然气节点流量向量；ΦS、ΦL分别为热源功率、热负荷功率向量；Cs、Cr分别为与供热网、回热网的拓扑和流量有关的系数矩阵；Ts,load、Tr,load分别为负荷节点的供热、回热温度列向量；bs、br分别为与供热温度、回热温度有关的列向量。

等式约束还包括耦合设备约束，见式(13)—(15)。

2.3 不等式约束

不等式约束包括各个变量的上下限、电力系统支路传输有功功率约束、天然气压缩机加压比约束：

xmin≤x≤xmax;

(20)

Pl,min≤Pl≤Pl,max,l∈Nl;

(21)

(22)

式(20)—(22)中：变量下标加后缀max、min分别表示变量的上、下限，下同；Pl为电网传输线路l的功率；kcom为压缩机加压比；Nl为电力系统中输电线路集合。

3 AND算法介绍

对于一个形式如下的优化问题[20,23]

(23)

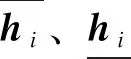
引入松弛变量li和ui(i=1，2)，其中的每个元素均不小于0，式(23)转化为

(24)

对式(24)引入拉格朗日乘子，构造对数壁垒罚函数，再消去松弛变量的非负性约束，得到增广拉格朗日函数：

(25)

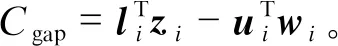
根据卡罗需-库恩-塔克(Karush-Kuhn-Tucker，KKT)条件，对式(25)求偏导，得到非线性方程组，再使用牛顿-拉夫逊法得到简化修正方程，即

(26)

式中：

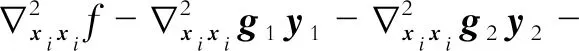
H12=H21；

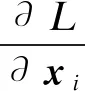
∇xihi(xi)(zi+wi)=0，i=1,2，j=1,2；

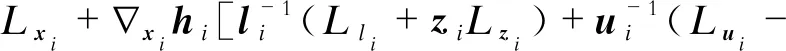
wiLwi)].

式(26)可简记为

KΔN=Ψ.

(27)

式中ΔN为原优化问题式(23)的精确牛顿方向。

因式(24)中含有2个耦合等式约束g1和g2而无法对变量x1和x2独立计算，考虑将变量分为2组：(x1,y1,l1,u1)和(x2,y2,l2,u2)，AND解耦法求解思路是在计算第一组变量问题时将第二组变量视作常数，化为只含有第一组变量的方程，反之亦然。将式(24)分解为以下2个优化子问题进行求解：

(28)

(29)

式(28)、(29)中带“～”符号的为常量，数值为上次迭代计算出的值。

同样，根据KKT条件对子问题构造的增广拉格朗日函数求偏导，得到非线性方程组，再使用牛顿法得到2个子问题的简化修正方程分别为：

(30)

(31)

式(30)、(31)也可以合并写成如下形式：

(32)

式(32)同样可简记为

(33)

式中ΔA为原优化模型的近似牛顿方向。

当满足解耦条件时，原优化问题便可分解为多个子问题，解耦判据的推导和证明见文献[15]。使用近似牛顿方向代替精确牛顿方向进行求解，解耦后子问题修正方程的维数减小，子问题只需要迭代1次，不需要求出最优解，减少了计算量。

4 求解电-热-气IES最优能流问题的AND算法

4.1 集中式规划模型的分解

依据AND算法，电力系统、热力系统、天然气系统可以在未知对方规划模型的情况下，通过交替优化子问题，只需要交互部分变量信息，便能实现电-热-气IES的分布式协同优化。因为三者隶属不同能源供应商，彼此无法获得对方的详细参数，本文假设存在监管、协调能源供应的第三方管理机构，管理机构对多能源系统进行统筹协调，使电、热、气的能源供应能够保证负荷安全稳定运行。为满足运行需要，电力系统、热力系统、天然气系统要向管理机构传递必要的变量，管理机构再向这三者传递所需的运行参数信息。因此本文假定所需的必要运行参数信息可以在这3个系统的优化决策过程中传递[12,24]。

下文给出由AND解耦法得到电、热、气子问题的具体形式，并从物理意义对目标函数释义。

4.1.1 电网子问题

对于电网主体，优化目标为电网运行成本最小，电网的电源为风电、光伏、燃气轮机、大电网。风电、光伏的投资与经营者都是微电网，因此不计运行成本，电网子问题的目标函数为燃气轮机发电成本与向大电网购电成本之和最小。

(34)

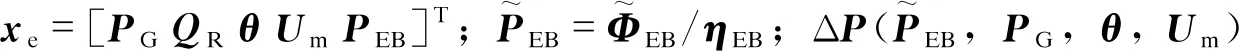
4.1.2 热网子问题

对于热网主体，优化目标为热网运行成本最小，热网的热源为电锅炉、燃气锅炉，电锅炉与燃气锅炉的能源供应分别来自电网与气网。因此热网子问题目标函数为电网中电锅炉购电与气网中燃气锅炉购气费用之和最小。

(35)

4.1.3 气网子问题

对于气网主体，优化目标为气网运行成本最小，气网由天然气气源供气，气网负荷包含燃气轮机与燃气锅炉，反映在目标函数中，气网子问题目标函数为气源购气成本之和最小。

(36)

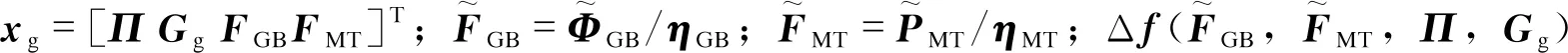
4.2 解耦计算流程

AND算法的计算流程如图3所示，从结构上可分为分解层和统筹层2层。分解层包含3个系统的子问题，数字①②表示计算的先后顺序；统筹层利用3个子问题产生的拉格朗日乘子和出力值进行信息交互与博弈，最终使得目标函数最小。

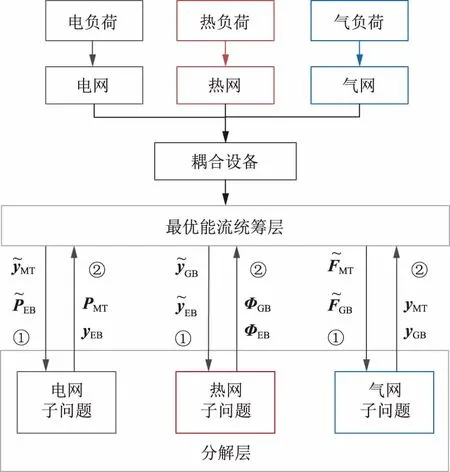
图3 AND法解耦电-热-气IES最优能流的示意图Fig.3 Schematic diagram of optimal energy flow of electricity-heat-gas IES decoupled by AND method

5 算例验证

5.1 算例设置

电-热-气IES算例图如附录图A1所示，选择经过修改的IEEE 30节点电力系统、英国巴里岛(以下简称“巴里岛”)32节点热力系统、比利时20节点天然气系统组成IES算例。耦合设备有燃气轮机、电锅炉、燃气锅炉。电锅炉效率ηEB=0.95，产热范围为5～20 MW；2个燃气锅炉效率ηGB均为0.9，产热范围均为5～30 MW；2个燃气轮机效率ηMT均为0.33，发电范围均为0～30 MW。

电网参数如下：节点1连接大电网，节点2连接光伏电站，节点22、27连接风电场，节点13、23连接燃气轮机，节点11连接电锅炉；电网有功负荷为189.2 MW；购电价格Ce=500元/MWh；光伏、风电最大出力均为10 MW。

热网参数如下：有3个热源，电锅炉在节点H32处，节点H30、H31连接燃气锅炉，本算例将巴里岛32节点系统[25]负荷统一扩大23倍，热网总负荷为49.772 MW。热网模型中：Ta=10 ℃，热源供热温度为70 ℃，热负荷出口温度为30 ℃。

天然气网的参数如下：节点G2、G8、G14、G20连接气源，节点G1、G4连接燃气轮机，节点G12、G16连接燃气锅炉。气网其他参数见附录表A1—A3。天然气模型中：zcom=0.03，LHVNG=9.7 kWh/m3。

实验中软件环境为MATLAB 2016b，在CPU型号为Intel i5-10400F、内存为16 GB的个人电脑上运行算例。

5.2 计算结果分析

本文构建模型的决策变量包括：电力系统中各电源出力PG与QR，电锅炉消耗的功率PEB；热力系统中热源(电锅炉、燃气锅炉)出力ΦEB、ΦGB；天然气系统中气源出力Gg和燃气轮机、燃气锅炉消耗的功率FMT、FGB。则决策变量为xde=[PGQRPEBΦEBΦGBGgFMTFGB]T，决策变量初值为xde0，上下限分别为xde,max和xde,min。

在文献[26]内点法的基础上进行编程，收敛条件与文献[26]中相同, 取收敛精度为10-6。设决策变量初值为xde0=αxde,min+(1-α)xde,max，对α不同取值情况进行计算，目标函数﹝式(16)﹞与补偿间隙收敛曲线如图4、图5所示。

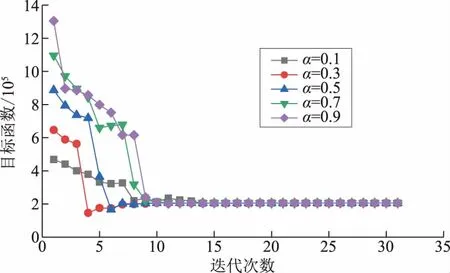
图4 目标函数迭代收敛曲线Fig.4 Iterative convergence curves of objective function

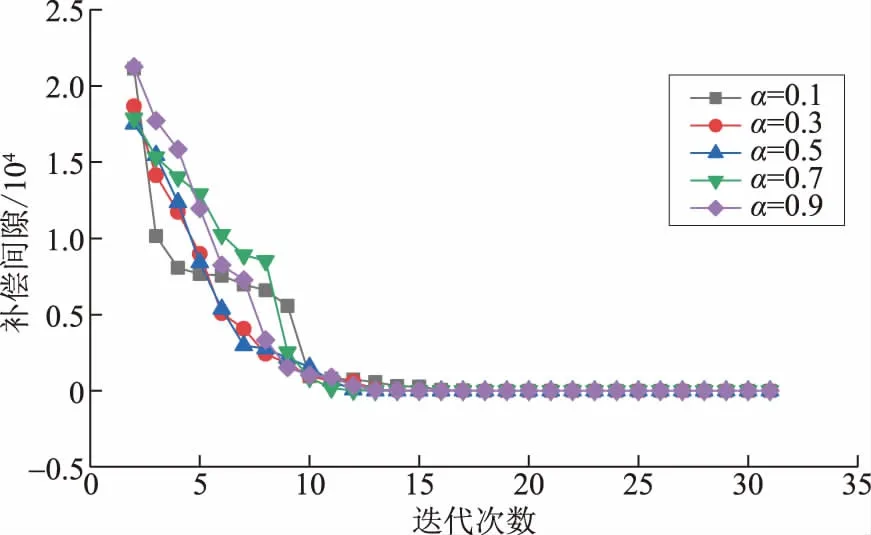
图5 补偿间隙收敛曲线Fig.5 Convergence curves of complementary gap

从图4、图5可以看出，在决策变量设置不同初值的情况下，迭代过程中目标函数、补偿间隙变化趋势基本一致，都是逐渐减小，最终趋近于0。由此可见，AND算法对初值不敏感，对于不同初值，可以稳定、快速收敛，得到相同的解，避免了初值选取对计算性能的影响。

为进一步验证AND算法求解电-热-气IES最优能流问题的正确性和有效性，取α=0.5，采用集中式内点法(centralized interior point method，CIPM)和AND算法计算所设置算例，时间长度为1 h，将计算结果进行比较。2种算法优化结果见表1—表3，目标函数与补偿间隙收敛曲线如图6、图7所示。

表1 设备出力比较Tab.1 Comparisons of equipment output

表2 运行成本比较Tab.2 Comparisons of operating costs

表3 算法性能比较Tab.3 Algorithm performance comparisons

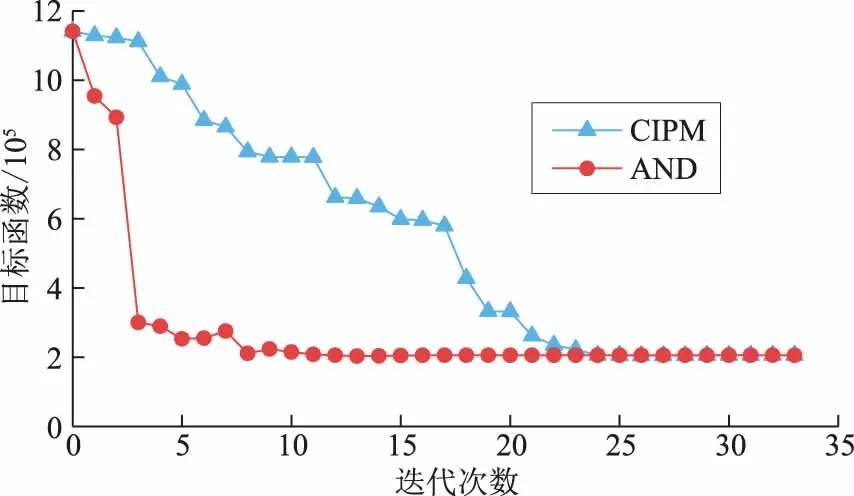
图6 目标函数迭代收敛曲线Fig.6 Iterative convergence curves of objective function

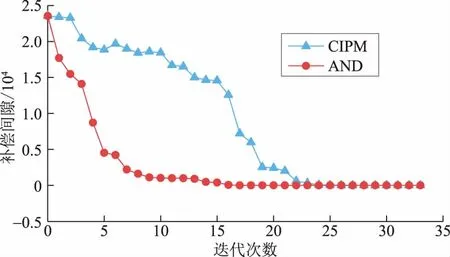
图7 补偿间隙收敛曲线Fig.7 Convergence curves of complementary gap

对比表1—表3可知，AND算法最后一次迭代时电-热-气IES等式约束最大失配值小于10-6，说明满足等式约束，因此得到的解是可行的。2种算法计算出电、热、气网各设备出力结果一致，运行成本误差小于10-3元，即AND算法能得到与CIPM相同的最优解，说明本文所提算法的正确性。

为更好说明AND算法的高效性，分别采用修改的IEEE 30、IEEE 118电网与巴里岛热网、比利时20节点气网构成IES，增加时段数以构成更大规模测试算例，使用2种算法的计算结果见表4。

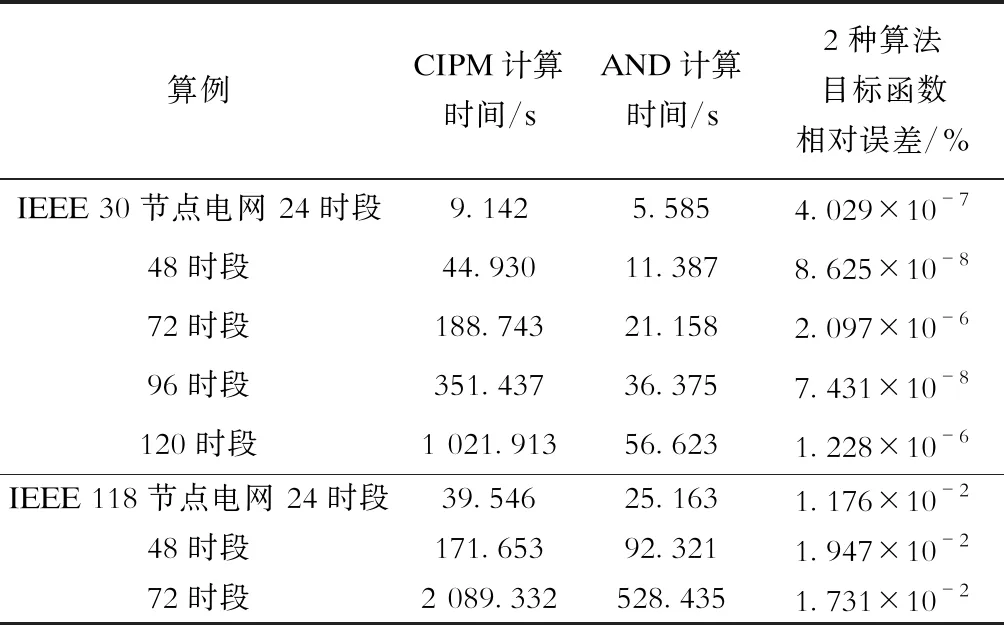
表4 大规模算例下算法性能比较Tab.4 Algorithm performance comparisons under large-scale examples

结合表3、表4与图5、图6看出，AND算法计算速度比CIPM快，求解大规模算例时AND算法在时间上的优越性更为突出。这是由于AND算法解耦后，计算数据量和修正矩阵规模小，因此AND算法所需峰值内存小于CIPM算法，例如在计算IEEE 30节点120时段算例时，CIPM算法在计算过程中会提示“内存不足”，而AND算法则不会出现这个问题。电、热、气子问题之间只需传递耦合设备出力和乘子2组变量，系统间信息传输量少，也使得AND算法计算时间比CIPM短。AND算法虽然忽略了部分信息，但是其修正方向与精确牛顿方向相近，因此具有较快的收敛速度和较高的精度，能够满足工程实际要求。此外，AND算法还具有无需对参数进行人为调整的优秀特性。

6 结束语

本文基于近似牛顿分解法提出一种求解电-热-气IES最优能流问题的分布式算法，通过测试算例验证了算法的准确性和有效性。所提算法将不同能源主体的系统解耦计算，各子系统之间只需要传递必要的信息，而各个系统自身的拓扑信息、私有数据和变量信息被保护起来，形成了保证隐私信息不泄露的交互模式。所提算法计算时间能够满足工程实际的要求，能源系统间信息交互量少，实现了电力系统、热力系统、天然气系统分布式优化。

本文所提方法针对电-热-气IES稳态能流进行了分布式优化求解，在后续研究中，将完善模型，例如在模型中加入储能、考虑气网的动态特性等，研究多时段情况下的分布式优化。