行波管与混响室噪声试验等效转换方法研究

刘泽锋，单雪利，于田霖，景岩

（中国航空综合技术研究所，北京 100020）

引言

随着高超声速飞行器的不断发展及冲压发动机的广泛应用，航空产品正面临着越来越严酷的噪声环境，机载舱内设备所承受的噪声声压可达160 dB，而冲压发动机附近声压更可高达180 dB[1,2]。噪声环境对航空产品带来的危害将越来越难以忽视，越来越多的航空产品需要通过实验室噪声环境试验来考核并提升其对噪声环境的适应能力。

目前，对航空产品的噪声环境模拟主要有行波管与混响室两种试验方式。就试验声场形式而言，混响室更贴合于舱内设备所经受的噪声环境，行波管更适合于模拟外挂及蒙皮等所承受的噪声环境。然而，混响室受限于其声场产生方式，存在诸如低频段简正频率不足、声压级起伏较大，特别是难以产生较高的声压级等问题，越来越无法满足高超声速飞行器航空产品噪声试验的需要。另一方面，行波管则具有频谱相对均匀、易产生低频声场，结构相对简单，尤其是可以实现较高声压频谱控制（目前国内外较先进的行波管试验设备可实现总声压172 dB以上的噪声频谱控制），因此航空航天领域逐渐出现以行波管近似替代混响室进行舱内设备噪声试验的相关研究及工程应用[2-4]。Smallwood[5]认为在相同声谱下，混响室产生的漫射波更易于激发产品的高频响应；空军怀特实验室[6]的研究人员则指出声频率在大于产品一阶固有频率且小于数百赫兹的范围内时，行波管产生的自由行波更易于激发产品的响应，而在更高的频率范围内，两种声场的试验效应几乎相同；沈㠙[7]通过理论分析指出从产品响应角度考虑，声场直接激发的响应通常比较小，主要是激发频率范围内所有简正频率而引起产品响应，因而不同声场的影响较小。

目前从产品响应角度出发进行的行波管近似替代混响室进行舱内设备噪声试验的研究还相对欠缺。本文针对采用混响室对舱内设备开展高量级噪声试验存在的局限性，以典型舱内设备为试验件，从响应的角度出发，采用行波管与混响室对比试验的方式，研究提出两种试验方式的近似等效转换方法。

1 理论研究

1.1 声场中试验件的响应研究

噪声环境使处于其中的试验件受到分布在其表面的随机脉动压力p(t,x)，噪声问题实质上是试验件在多维随机压力下的结构响应问题，建立试验件的运动微分方程如下：

式中：

x—广义空间坐标系；

q n(t)—n阶模态的广义坐标；

φn(x)为满足边界条件的第n阶模态形状函数；

ωn—第n阶模态频率；

M—质量；

C—阻尼矩阵；

K—刚度算子。

其通解为：

对式（1）两边乘以φn(x)，并在全部外表面广义坐标l上积分，利用模态的正交性，得：

对式（3）两边进行傅里叶变换，得：

式中：

Sqn—qn(t)的傅里叶变换；

响应的傅里叶变换 Sy(ω)可以表示为

在许多实际情况下，特别是在地面试验时，可以认为噪声是平稳随机过程[8]。因而，可以采用周期图法得到响应的功率谱密度

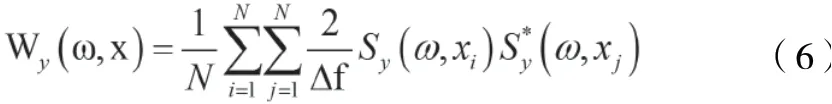
式中：

*—共轭；

N—周期图的帧数；

△f—频率分辨率。

结合式（4）、式（5）和式（6）得响应的功率谱与载荷的功率谱密度关系为：

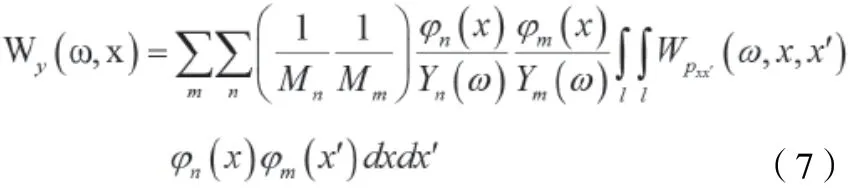
式中：

Yn(ω)—第n阶模态传递函数；

由此可以看出，试验件上任意一点的响应由结构的模态、传递函数、声压的互谱密度共同决定。结构的模态、传递函数均为结构的固有属性，因而对一特定产品来说，声压的互谱密度将决定结构的响应。

引入空间相关系数γ（ω，ε），其定义如下：

将式（8）代入式（7）中，得：

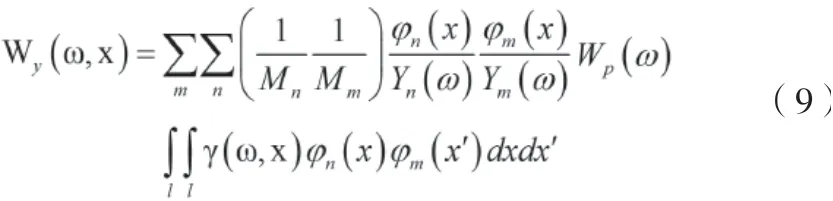
式中：

Yn(ω)—n阶模态传递函数，反映了响应对频率具有强烈的选择性，而反映了空间相关系数对结构响应的影响。

1.2 响应等效理论

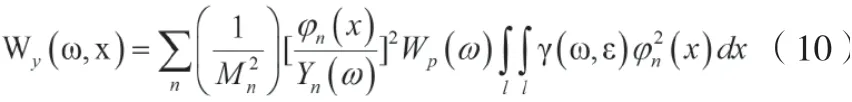
γ行(ω,ε)、γ混(ω,ε)—行波管及混响室内声场空间相关系数。

设Z(ω)为行波管与混响室的声场转换系数，其定义为：

将式（11）与式（12）结合，得：

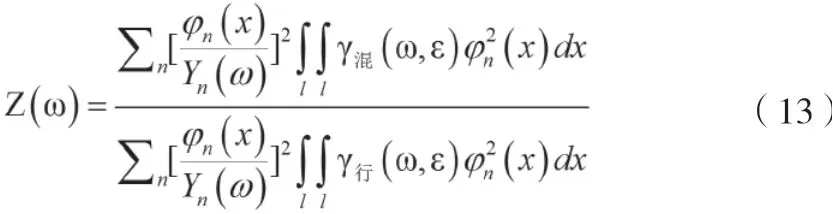
式中空间相关系数γ行(ω,ε)、γ混(ω,ε)需通过试验的方法测定，为离散值。因此，需将式（13）进行离散化以求解。在试验件表面布置等间距的i*j*k个点，将试验件表面分解为i*(j-1)*(k-1)个部分，广义积分变为

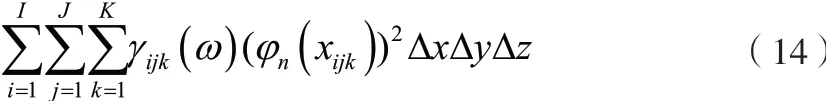
其中φn(xijk)可从模态仿真/试验结果上获取。

将式（14）代入式（12），转化为向量表示，如式（15）所示。

综上可得：

通过上述分析可知，经离散化后，对同一试验件，行波管与混响室声场转换系数Z(ω)可由两者声场空间相关系数得到，也就是说虽然相关系数的影响很难用响应等效的方法完全代替，但可以通过调整声压和频谱的方法来使两种声场作用下结构上特定点响应一致。

2 试验研究及验证

试验件不同的结构特征不仅影响其自身响应特性及所承受的声载荷，同时也将对声场产生不同的影响，例如圆柱形结构与平面壁板结构在自身固有特性、承受声载荷及对声场的影响上都存在显著差异，难以一概而论。

为使试验结果更具有代表性与说服力，本次试验选取某型飞机上真实舱内设备作为试验件，其材料、结构有一定代表性。该设备主要由铝合金壳体、印制板（FR4）、连接器等构成。

噪声试验控制谱型选取GJB 150.17A-2009《军用装备实验室环境试验方法 第17部分：噪声试验》中推荐的试验谱，总声压级145 dB，见表1。

表1 1/3倍频程声压级

2.1 空间相关系数的获取

声场转换系数Z（ω）取决于不同声场间空间相关系数的比值，因此首先需要获得声场空间相关系数。

试验件放入试验设备后，会成为其声场内部的一个或多个壁面，将使声波的传播更加复杂，其空间相关特性也将发生变化，使得理论分析变得非常困难的，只能采用试验方法获取[8]。而空间相关系数无法直接测定，需首先采用声传感器测量声压，进而根据式（8），通过数据处理获得。

以试验件前面板一个顶点为原点，分别以宽、高、长为X、Y、Z轴建立空间直角坐标系。考虑到行波管内声场沿截面与轴向空间相关特性存在差异，以试验件XY面和Z轴向分别计算空间相关系数。试验期间照片如图1和图2所示。

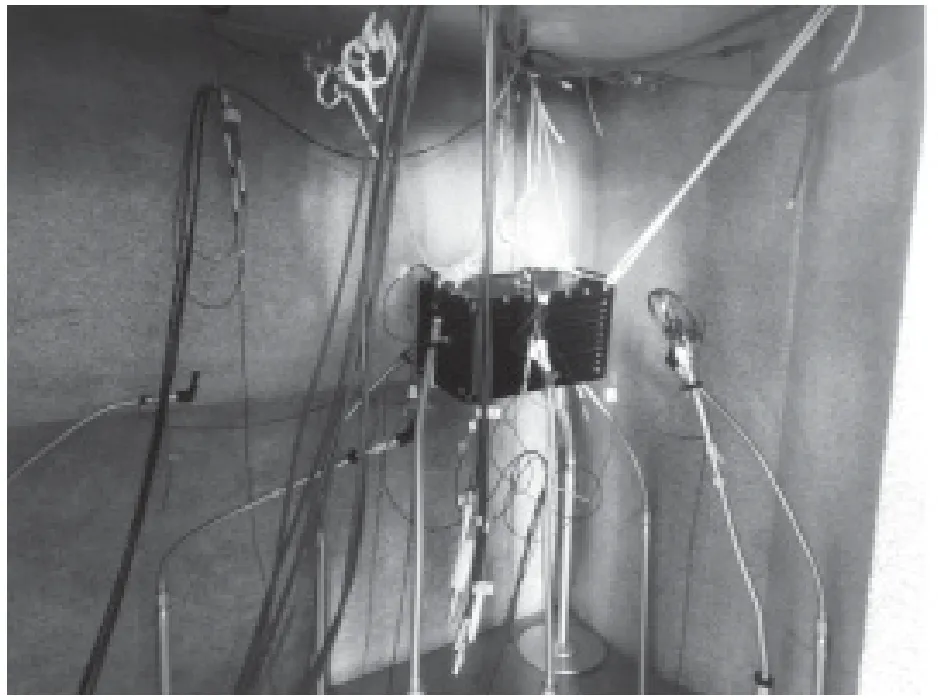
图1 混响室内试验件实际安装状态

根据式（8），以前面板中心O0为基准点，经归一化和曲线平滑处理后，获得各测点相对于基准点的空间相关系数曲线，选取部分曲线如图3~6。其中，横坐标为波数为频率，c为声速，ε为测点与基准点间距离。

图3 截面横向空间相关系数（行波管）

行波管内声场横向空间相关系数在低频段接近于常数，在高频段接近零阶贝塞尔函数；轴向空间相关系数在低频段接近于余弦函数，在高频段接近零阶贝塞尔函数，该结果表明行波管内声场在低频段声场接近平面阵声波，高频段存在许多近似均匀随机入射的平面声波。

从图5和图6可以看到，混响室内各轴向声场空间相关系数均在低频段接近于常数，在高频段接近零阶贝塞尔函数，该结果表明混响室内声场在各个方向存在近似均匀的平面阵声波。

图 2 行波管内试验件实际安装状态

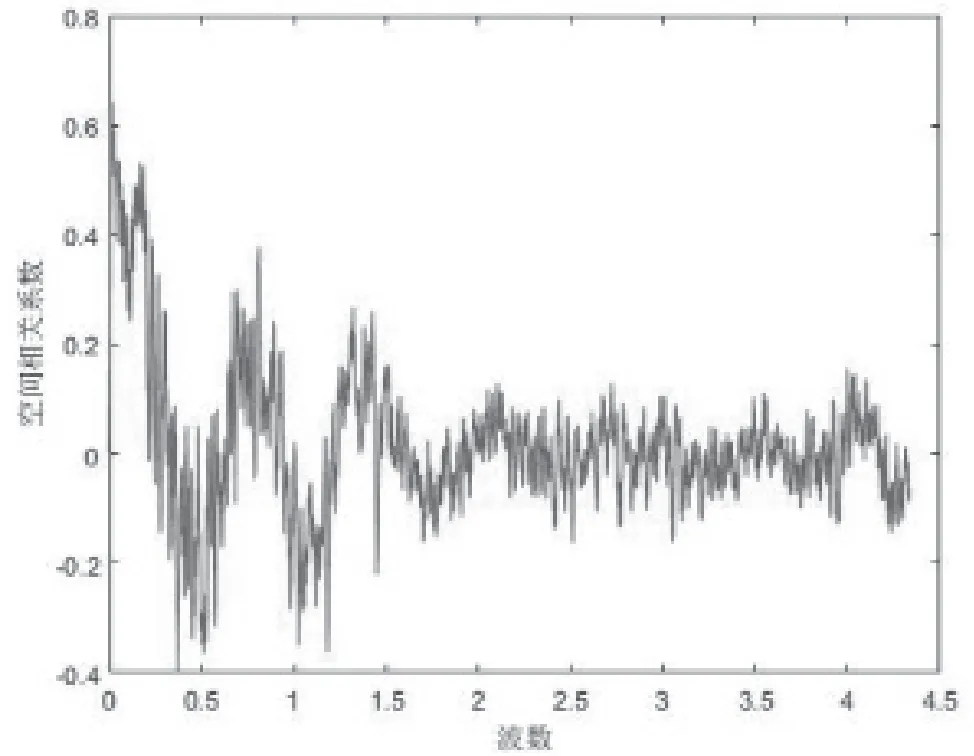
图5 试件XY面横向空间相关系数（混响室）

图6 试件Z轴向空间相关系数（混响室）

2.2 试验验证

图4 轴向空间相关系数（行波管）

在2.1中测试空间相关系数时，在试验件的前面中心位置上布置一个加速度传感器，选取前面板中心O0作为响应等效目标点。未对声谱修正时，行波管与混响室试验时O0处响应对比见图7。

图7 修正前目标点处响应功率谱密度

按2.1中方法将得到的混响室和行波管中关于O0归一化的空间相关系数代入式（17）中，经计算得到行波管与混响室之间的声场转换系数Z(ω)。这里需要说明的是，本文主要为方法性研究，为便于试验实施，本次验证试验采用Z(ω)对混响声谱进行修正，使其响应与行波管试验时一致，可以达到验证所提方法正确性的目的。

由于噪声试验一般采用1/3倍频程声压级控制，将Z(ω)转换为声压级修正系数P(ω)=10log Z(ω)，最终求得修正后的1/3倍频程声压控制谱如表2所示。

表2 修正后1/3倍频程控制谱

采用修正后的声谱，其他试验条件不变，进行混响室噪声试验，目标点处与混响室试验时响应对比如图8所示。

图8 修正后目标点处响应功率谱密度

修正声谱后，行波管试验中目标点处响应的功率谱密度与混响室试验接近，响应的均方根值差别由41 %降低至6.5 %，可以满足工程要求，证明了所提出的近似替代方法的可行性及正确性。此外，试验件在混响室试验时低频段响应明显低于行波管试验时，存在这种差异的原因是混响室在低频段简正频率数呈现明显不足，难以激发被试品低频响应。

3 结论

本文从响应模拟的角度出发，基于响应等效理论，提出了一种行波管与混响室噪声试验等效转换的方法：首先分别测定舱内设备放入行波管和混响室后声场空间系数，进而得到声场间的转换系数以修正声谱，采用修正后的声谱开展噪声试验。采用该等效转换方法进行了验证试验，混响室试验中试验件上目标点响应与行波管试验时响应接近，证明了所提方法的可行性及准确性。该近似转换方法为舱内设备高声压级噪声试验难以开展的问题提供了一种可行的解决方法，在工程上具有切实的应用价值。